9.4 矩形、菱形、正方形(第1课时)课件(共32张PPT)-2023-2024学年八年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 9.4 矩形、菱形、正方形(第1课时)课件(共32张PPT)-2023-2024学年八年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 18:22:08 | ||
图片预览


文档简介
第9章 · 中心对称图形——平行四边形
9.4 矩形、菱形、正方形(1)
第1课时 矩形及其性质
学习目标
1. 理解矩形的概念;
2.探索并证明矩形的性质定理;
3.能运用矩形的性质定理解决问题.
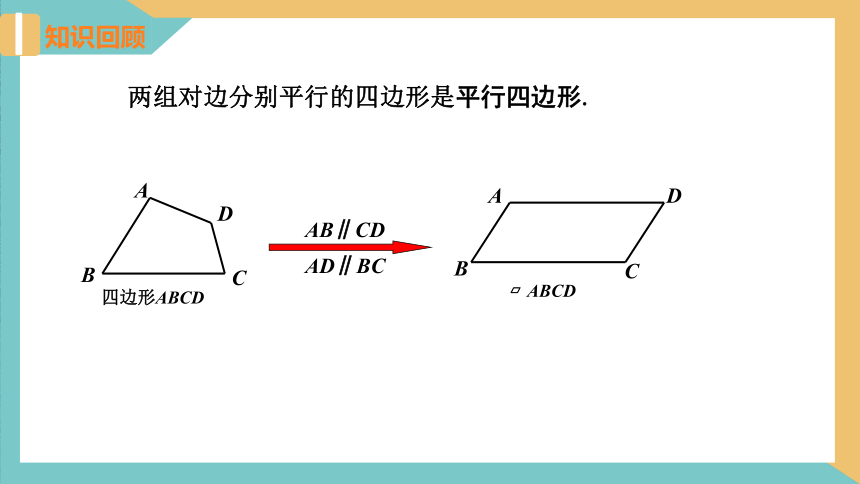
知识回顾
两组对边分别平行的四边形是平行四边形.
A
B
C
D
四边形ABCD
AB∥CD AD∥BC
B
D
?ABCD
A
C
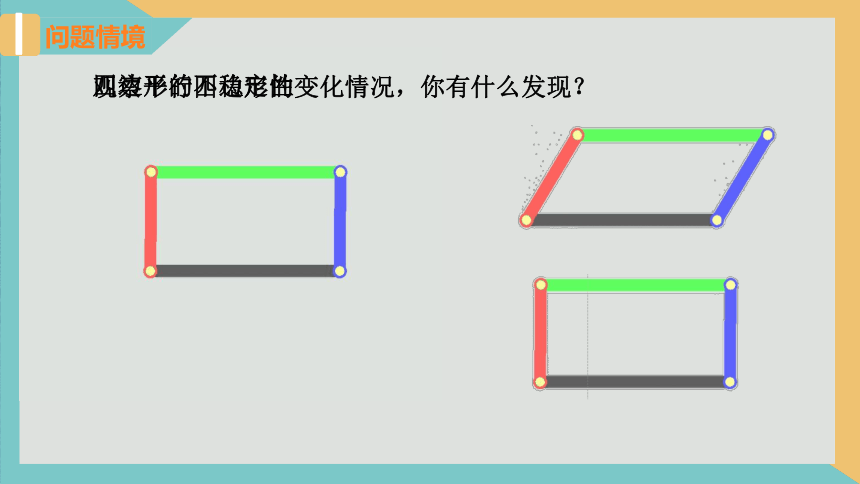
问题情境
四边形的不稳定性
观察平行四边形的变化情况,你有什么发现?
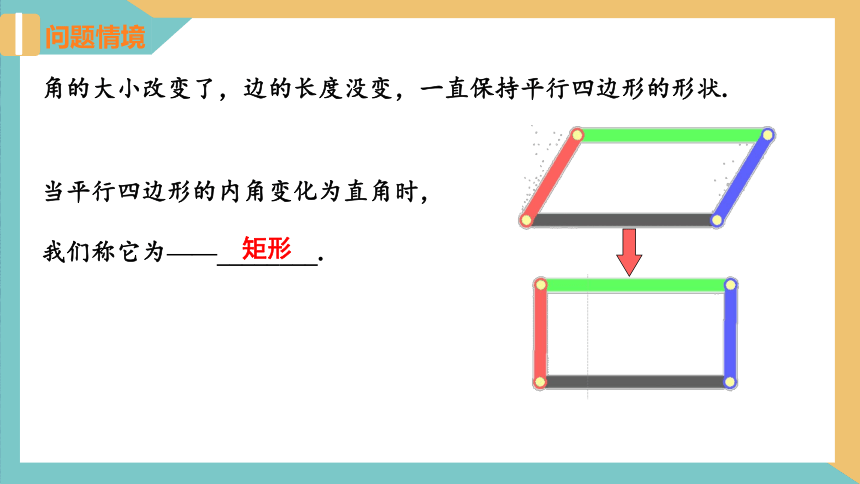
问题情境
角的大小改变了,边的长度没变,一直保持平行四边形的形状.
当平行四边形的内角变化为直角时,我们称它为——________.
矩形
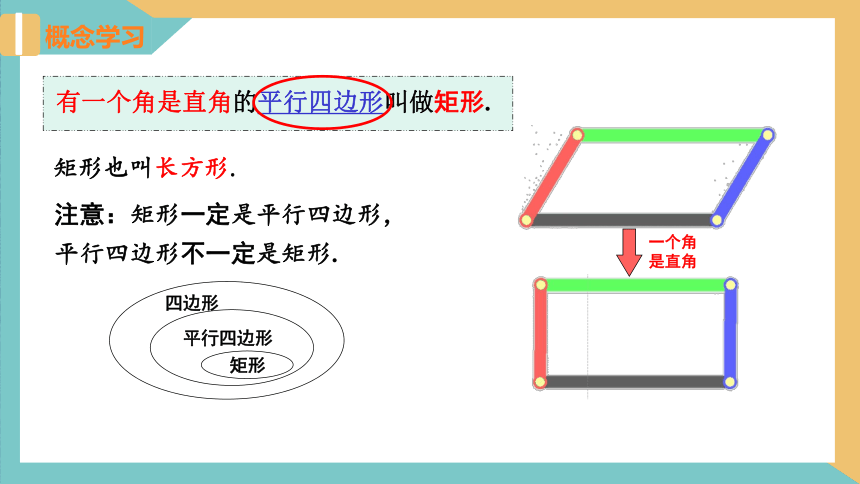
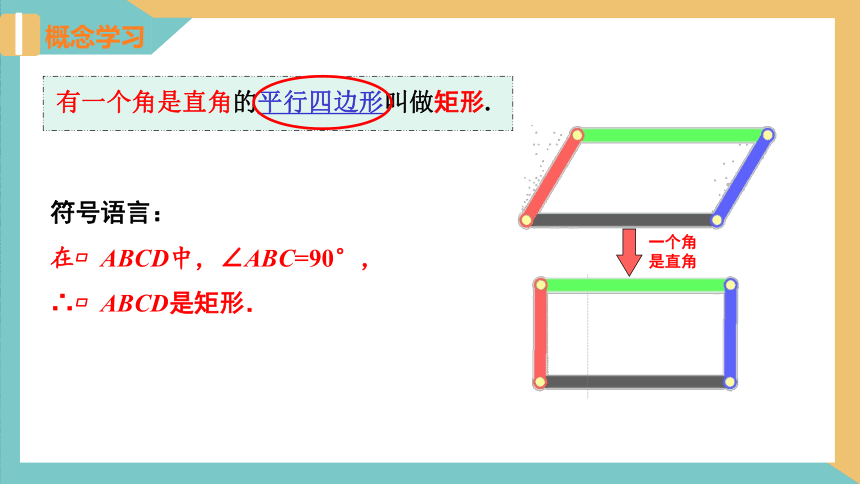
概念学习
一个角是直角
有一个角是直角的平行四边形叫做矩形.
矩形也叫长方形.
注意:矩形一定是平行四边形,
平行四边形不一定是矩形.
四边形
矩形
平行四边形
概念学习
一个角是直角
有一个角是直角的平行四边形叫做矩形.
符号语言:
在?ABCD中,∠ABC=90°,
∴?ABCD是矩形.
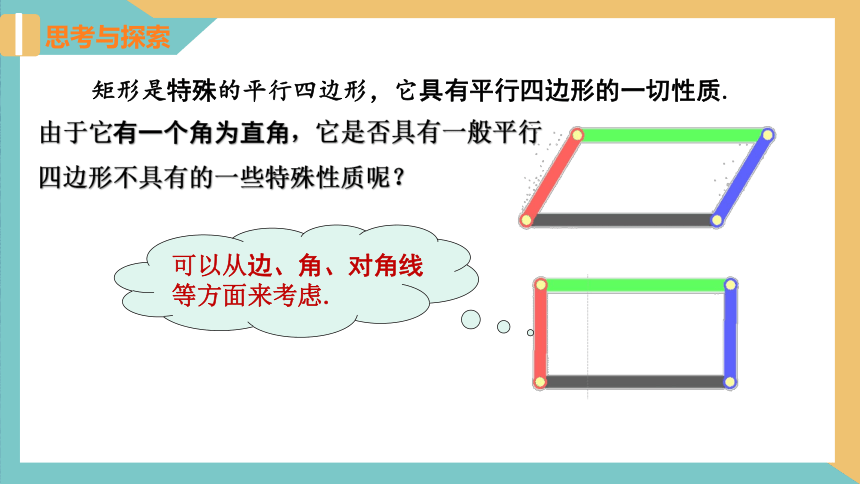
由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
矩形是特殊的平行四边形,它具有平行四边形的一切性质.
思考与探索
可以从边、角、对角线等方面来考虑.
思考与探索
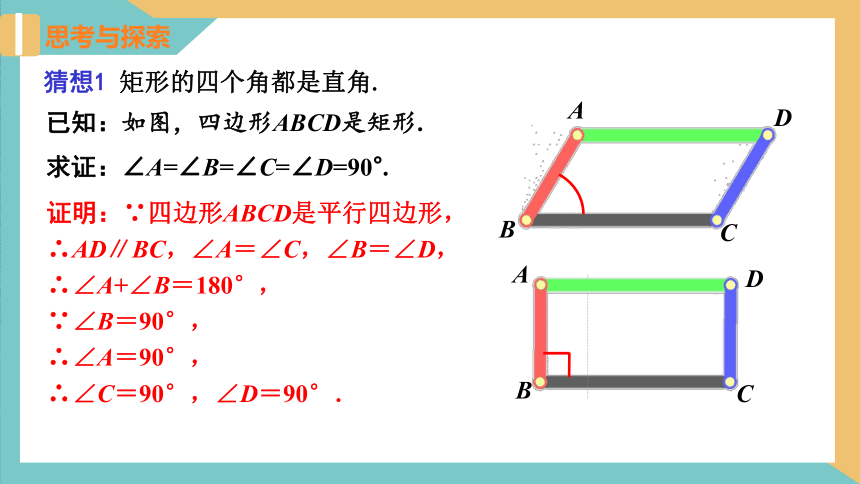
猜想1 矩形的四个角都是直角.
B
A
D
C
B
A
D
C
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
∵∠B=90°,
∴∠A=90°,
∴∠C=90°,∠D=90°.
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
思考与探索
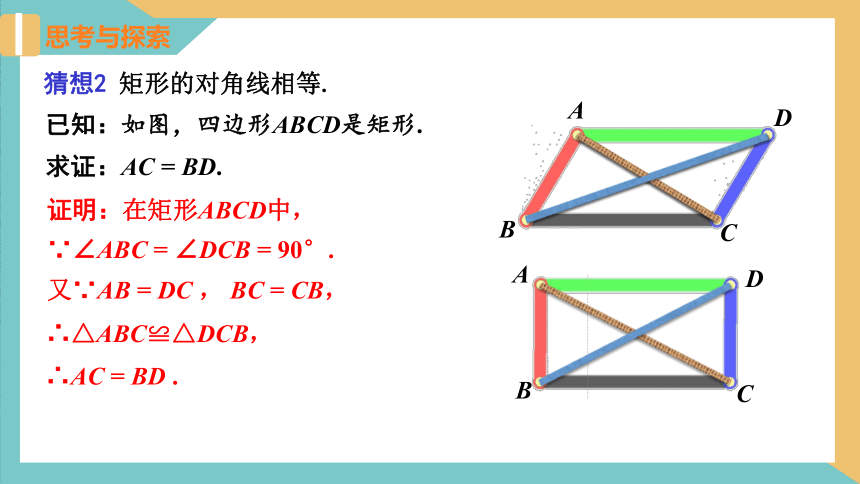
猜想2 矩形的对角线相等.
B
A
D
C
B
A
D
C
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°.
又∵AB = DC , BC = CB,
∴△ABC≌△DCB,
∴AC = BD .
已知:如图,四边形ABCD是矩形.
求证:AC = BD.
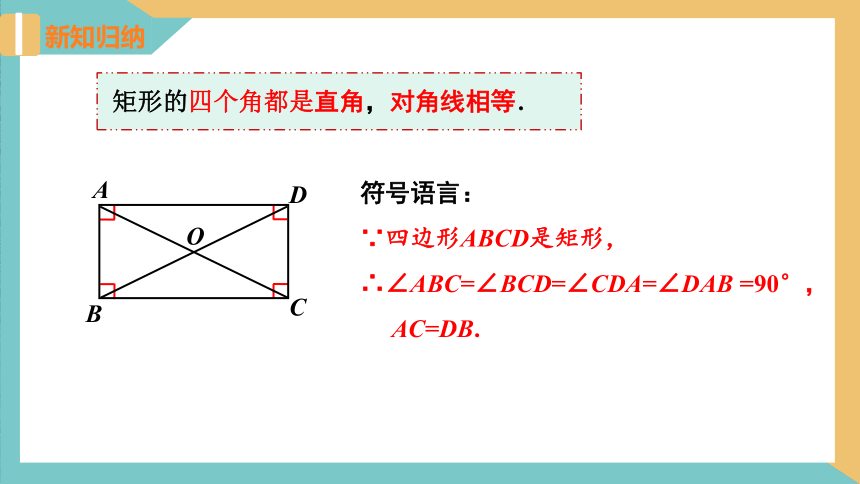
新知归纳
矩形的四个角都是直角,对角线相等.
符号语言:
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=∠CDA=∠DAB =90°,
AC=DB.
B
A
D
C
O
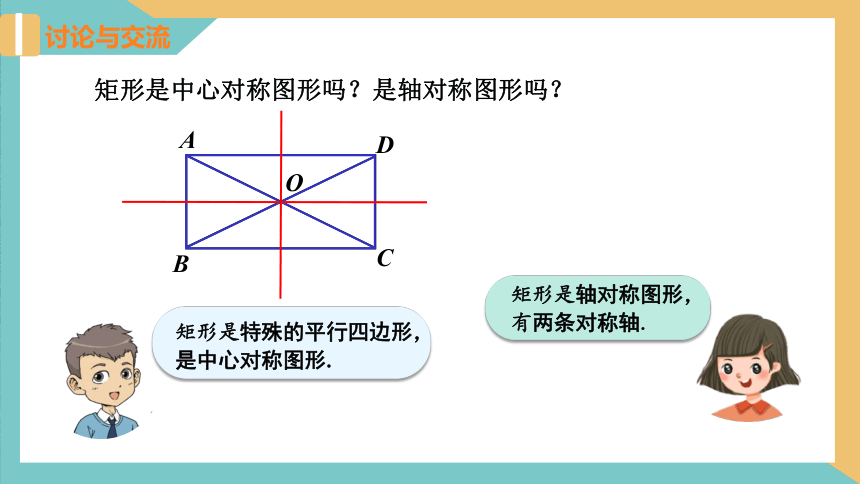
讨论与交流
矩形是中心对称图形吗?是轴对称图形吗?
B
A
D
C
O
矩形是特殊的平行四边形,是中心对称图形.
矩形是轴对称图形,有两条对称轴.
归纳提升
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}矩形
性 质
符号语言
图示
边
角
对角线
对称性
对边平行且相等
四个角都是直角
对角线互相平分且相等
B
A
D
C
O
l1
l2
既是中心对称图形又是轴对称图形
∵四边形ABCD是矩形,
∴AB∥CD,AD∥BC,
AB=CD,AD=BC.
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=
∠CDA=∠DAB=90°.
∵四边形ABCD是矩形,
∴OA=OC,OB=OD
AC=BD.
对称中心是对角线的交点O,对称轴是直线l1和l2.
新知巩固
1.矩形的定义中有两个条件:一是___________,二是_______________.
平行四边形
有一个角是直角
2.下列说法不正确的是 ( )
A. 矩形是平行四边形
B. 矩形的对角线互相平分
C. 有一个角是直角的四边形是矩形
D. 矩形既是轴对称图形又是中心对称图形
C
新知巩固
3.下列性质中,矩形不一定具有的是 ( )
A.对角线相等 B.四个角都相等
C.对角线垂直 D.是轴对称图形
C
4 .矩形具有而平行四边形不具有的性质是 ( )
A.两组对边分别平行 B.对角相等
C.对角线互相平分 D.对角线相等
D
例题讲解
证明: ∵四边形ABCD是矩形,
∴AC=BD,(矩形的对角线相等)
AO=CO=????????AC,BO=DO=????????BD,
(矩形的对角线互相平分)
∵AC=2AB,
∴AB=????????AC.
∴AO=BO=AB.
∴△AOB是等边三角形.
?
例 已知:如图,矩形ABCD的对角线AC、BD相交于点O,且 AC=2AB.
求证:△AOB是等边三角形.
A
D
B
C
O
例题讲解
变式1 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm. 求矩形对角线长.
A
D
B
C
O
解: ∵四边形ABCD是矩形,
∴AC=BD,(矩形的对角线相等)
AO=CO=????????AC,BO=DO=????????BD,
(矩形的对角线互相平分)
∴AO=BO.
∵∠AOD=120°,
∴∠AOB=60°.
∴△AOB是等边三角形.
∴AC=2OA=2AB=8cm.
?
矩形的面积呢?
在Rt△ABC中,BC=?????????????????????????=?????????????????=????.
∴矩形ABCD的面积=AB?BC=16????cm2.
?
例题讲解
变式2 利用矩形的性质,证明“直角三角形斜边上的中线等于斜边的一半”.
D
C
O
B
A
证明: 延长BO到D,使OD=BO,连接AD、DC.
已知:如图,在Rt△ABC中,∠ABC=90°,BO是中线.求证:BO = ????????AC ?
?
∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴?ABCD是矩形,
∴AC=BD,BO=???????? BD=???????? AC.
?
讨论与交流
1. 两条对角线把矩形分成____对全等三角形,其中有____对全等的直角三角形,____对全等的等腰三角形;
B
A
D
C
O
2. 两条对角线把矩形分成的4个等腰三角形的______相等,______相等.
4
2
2
腰长
面积
新知巩固
1.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
(1)△BEC是否为等腰三角形?证明你的结论.
A
D
B
C
E
解:(1)△BEC是等腰三角形. 证明如下:
∵四边形ABCD是矩形,
∴AD// BC,
∴∠DEC=∠BCE.
又∵EC平分∠BED,
∴∠DEC=∠BEC,
∴∠BCE=∠BEC,
∴BE=BC.
∴△BEC是等腰三角形.
新知巩固
(2)AB=1,∠ABE=45°,求BC的长.
解:(2)在△ABE中,
∵∠A=90°,∠ABE=45°,
∴∠AEB=∠ABE,
∴AE=AB=1,
Rt△ABC中,由勾股定理得BE=????????????+????????????=????????+????????=????.
∴BC=BE=????.
?
A
D
B
C
E
新知巩固
2.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥DB,交AB的延长线于点E.
(1) 求证:AC=EC;
A
B
C
D
O
E
证明:(1)∵四边形ABCD是矩形,
∴AC=DB,AB∥DC.
又∵CE∥DB,
∴四边形DBEC是平行四边形,
∴DB=EC,
∴AC=EC.
新知巩固
(2)解:∵在矩形ABCD中,BO=4,
∴BD=2BO=2×4=8.
∵∠DBC=30°,
∴CD=????????BD=????????×8=4,
∴AB=CD=4,AE=AB+BE=AB+CD=8.
在Rt△BCD中,
BC=?????????????????????????=?????????????????=4????.
∴四边形AECD的面积=????????×(4+8)×4????=24????.
?
(2) 若∠DBC=30° , BO=4 ,求四边形AECD的面积.
A
B
C
D
O
E
新知巩固
变式 如图,在△AEC中,AC=EC,B是AE的中点,O在AC上,且OA=OC,连接BO,并延长至点D,使OD=OB.
求证:四边形ABCD是矩形.
证明:∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
∵AC=EC,B是AE的中点,
∴CB⊥AE,
∴∠ABC=90°,
∴?ABCD是矩形
(有一个角是直角的平行四边形是矩形).
A
B
C
D
O
E
课堂小结
9.4 矩形、菱形、正方形(1)
矩形的概念
矩形的性质
一般性质
特殊性质
当堂检测
1.矩形不一定具有的性质是( )A.对角线互相平分 B.对角线互相垂直C.对角线相等 D.是轴对称图形
B
2.矩形具有而平行四边形不一定具有的性质是( )A.对角相等 B.对边相等C.对角线相等 D.对角线互相平分
C
当堂检测
3. 如图,在矩形ABCD中,对角线AC,BD交于点O, 下列说法错误的是( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
A
B
C
D
O
C
当堂检测
4. 矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形,
( )个直角三角形.
A.2 B.4 C.6 D.8
B
B
A
B
C
D
O
当堂检测
5. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为________.
80°
6. 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=4 cm,则矩形ABCD的对角线长为_________.
8 cm
A
B
C
D
O
7.如图,在矩形ABCD中,AE平分∠BAD,交边BC于点E,若ED=5,EC=3,则矩形ABCD的周长为________.
当堂检测
A
B
C
D
E
22
8.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_________.
(7)
(8)
????????
?
当堂检测
9.如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解:∵ △AOB、 △BOC、 △COD和△AOD
四个三角形的周长和为86cm,
又∵ AC=BD=13cm(矩形的对角线相等)
∴ AB+BC+CD+DA = 86-2(AC+BD)
= 86-2×2×13
即矩形ABCD的周长等于34cm.
= 34cm
即 AB+BC+CD+DA+2(AC+BD) =86
A
B
C
D
O
10.如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值.
解:连接OP.
∵四边形ABCD是矩形,
∴∠DAB=90°,OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC=????????S矩形ABCD=????????×6×8=12.
在Rt△BAD中,由勾股定理得BD=10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴????????AO·PE+????????DO·PF=12,即5PE+5PF=24,
∴PE+PF=????????????.
?
A
B
C
D
O
P
E
F
当堂检测
9.4 矩形、菱形、正方形(1)
第1课时 矩形及其性质
学习目标
1. 理解矩形的概念;
2.探索并证明矩形的性质定理;
3.能运用矩形的性质定理解决问题.
知识回顾
两组对边分别平行的四边形是平行四边形.
A
B
C
D
四边形ABCD
AB∥CD AD∥BC
B
D
?ABCD
A
C
问题情境
四边形的不稳定性
观察平行四边形的变化情况,你有什么发现?
问题情境
角的大小改变了,边的长度没变,一直保持平行四边形的形状.
当平行四边形的内角变化为直角时,我们称它为——________.
矩形
概念学习
一个角是直角
有一个角是直角的平行四边形叫做矩形.
矩形也叫长方形.
注意:矩形一定是平行四边形,
平行四边形不一定是矩形.
四边形
矩形
平行四边形
概念学习
一个角是直角
有一个角是直角的平行四边形叫做矩形.
符号语言:
在?ABCD中,∠ABC=90°,
∴?ABCD是矩形.
由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
矩形是特殊的平行四边形,它具有平行四边形的一切性质.
思考与探索
可以从边、角、对角线等方面来考虑.
思考与探索
猜想1 矩形的四个角都是直角.
B
A
D
C
B
A
D
C
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
∵∠B=90°,
∴∠A=90°,
∴∠C=90°,∠D=90°.
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
思考与探索
猜想2 矩形的对角线相等.
B
A
D
C
B
A
D
C
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°.
又∵AB = DC , BC = CB,
∴△ABC≌△DCB,
∴AC = BD .
已知:如图,四边形ABCD是矩形.
求证:AC = BD.
新知归纳
矩形的四个角都是直角,对角线相等.
符号语言:
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=∠CDA=∠DAB =90°,
AC=DB.
B
A
D
C
O
讨论与交流
矩形是中心对称图形吗?是轴对称图形吗?
B
A
D
C
O
矩形是特殊的平行四边形,是中心对称图形.
矩形是轴对称图形,有两条对称轴.
归纳提升
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}矩形
性 质
符号语言
图示
边
角
对角线
对称性
对边平行且相等
四个角都是直角
对角线互相平分且相等
B
A
D
C
O
l1
l2
既是中心对称图形又是轴对称图形
∵四边形ABCD是矩形,
∴AB∥CD,AD∥BC,
AB=CD,AD=BC.
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=
∠CDA=∠DAB=90°.
∵四边形ABCD是矩形,
∴OA=OC,OB=OD
AC=BD.
对称中心是对角线的交点O,对称轴是直线l1和l2.
新知巩固
1.矩形的定义中有两个条件:一是___________,二是_______________.
平行四边形
有一个角是直角
2.下列说法不正确的是 ( )
A. 矩形是平行四边形
B. 矩形的对角线互相平分
C. 有一个角是直角的四边形是矩形
D. 矩形既是轴对称图形又是中心对称图形
C
新知巩固
3.下列性质中,矩形不一定具有的是 ( )
A.对角线相等 B.四个角都相等
C.对角线垂直 D.是轴对称图形
C
4 .矩形具有而平行四边形不具有的性质是 ( )
A.两组对边分别平行 B.对角相等
C.对角线互相平分 D.对角线相等
D
例题讲解
证明: ∵四边形ABCD是矩形,
∴AC=BD,(矩形的对角线相等)
AO=CO=????????AC,BO=DO=????????BD,
(矩形的对角线互相平分)
∵AC=2AB,
∴AB=????????AC.
∴AO=BO=AB.
∴△AOB是等边三角形.
?
例 已知:如图,矩形ABCD的对角线AC、BD相交于点O,且 AC=2AB.
求证:△AOB是等边三角形.
A
D
B
C
O
例题讲解
变式1 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm. 求矩形对角线长.
A
D
B
C
O
解: ∵四边形ABCD是矩形,
∴AC=BD,(矩形的对角线相等)
AO=CO=????????AC,BO=DO=????????BD,
(矩形的对角线互相平分)
∴AO=BO.
∵∠AOD=120°,
∴∠AOB=60°.
∴△AOB是等边三角形.
∴AC=2OA=2AB=8cm.
?
矩形的面积呢?
在Rt△ABC中,BC=?????????????????????????=?????????????????=????.
∴矩形ABCD的面积=AB?BC=16????cm2.
?
例题讲解
变式2 利用矩形的性质,证明“直角三角形斜边上的中线等于斜边的一半”.
D
C
O
B
A
证明: 延长BO到D,使OD=BO,连接AD、DC.
已知:如图,在Rt△ABC中,∠ABC=90°,BO是中线.求证:BO = ????????AC ?
?
∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴?ABCD是矩形,
∴AC=BD,BO=???????? BD=???????? AC.
?
讨论与交流
1. 两条对角线把矩形分成____对全等三角形,其中有____对全等的直角三角形,____对全等的等腰三角形;
B
A
D
C
O
2. 两条对角线把矩形分成的4个等腰三角形的______相等,______相等.
4
2
2
腰长
面积
新知巩固
1.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
(1)△BEC是否为等腰三角形?证明你的结论.
A
D
B
C
E
解:(1)△BEC是等腰三角形. 证明如下:
∵四边形ABCD是矩形,
∴AD// BC,
∴∠DEC=∠BCE.
又∵EC平分∠BED,
∴∠DEC=∠BEC,
∴∠BCE=∠BEC,
∴BE=BC.
∴△BEC是等腰三角形.
新知巩固
(2)AB=1,∠ABE=45°,求BC的长.
解:(2)在△ABE中,
∵∠A=90°,∠ABE=45°,
∴∠AEB=∠ABE,
∴AE=AB=1,
Rt△ABC中,由勾股定理得BE=????????????+????????????=????????+????????=????.
∴BC=BE=????.
?
A
D
B
C
E
新知巩固
2.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥DB,交AB的延长线于点E.
(1) 求证:AC=EC;
A
B
C
D
O
E
证明:(1)∵四边形ABCD是矩形,
∴AC=DB,AB∥DC.
又∵CE∥DB,
∴四边形DBEC是平行四边形,
∴DB=EC,
∴AC=EC.
新知巩固
(2)解:∵在矩形ABCD中,BO=4,
∴BD=2BO=2×4=8.
∵∠DBC=30°,
∴CD=????????BD=????????×8=4,
∴AB=CD=4,AE=AB+BE=AB+CD=8.
在Rt△BCD中,
BC=?????????????????????????=?????????????????=4????.
∴四边形AECD的面积=????????×(4+8)×4????=24????.
?
(2) 若∠DBC=30° , BO=4 ,求四边形AECD的面积.
A
B
C
D
O
E
新知巩固
变式 如图,在△AEC中,AC=EC,B是AE的中点,O在AC上,且OA=OC,连接BO,并延长至点D,使OD=OB.
求证:四边形ABCD是矩形.
证明:∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
∵AC=EC,B是AE的中点,
∴CB⊥AE,
∴∠ABC=90°,
∴?ABCD是矩形
(有一个角是直角的平行四边形是矩形).
A
B
C
D
O
E
课堂小结
9.4 矩形、菱形、正方形(1)
矩形的概念
矩形的性质
一般性质
特殊性质
当堂检测
1.矩形不一定具有的性质是( )A.对角线互相平分 B.对角线互相垂直C.对角线相等 D.是轴对称图形
B
2.矩形具有而平行四边形不一定具有的性质是( )A.对角相等 B.对边相等C.对角线相等 D.对角线互相平分
C
当堂检测
3. 如图,在矩形ABCD中,对角线AC,BD交于点O, 下列说法错误的是( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
A
B
C
D
O
C
当堂检测
4. 矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形,
( )个直角三角形.
A.2 B.4 C.6 D.8
B
B
A
B
C
D
O
当堂检测
5. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为________.
80°
6. 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=4 cm,则矩形ABCD的对角线长为_________.
8 cm
A
B
C
D
O
7.如图,在矩形ABCD中,AE平分∠BAD,交边BC于点E,若ED=5,EC=3,则矩形ABCD的周长为________.
当堂检测
A
B
C
D
E
22
8.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_________.
(7)
(8)
????????
?
当堂检测
9.如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解:∵ △AOB、 △BOC、 △COD和△AOD
四个三角形的周长和为86cm,
又∵ AC=BD=13cm(矩形的对角线相等)
∴ AB+BC+CD+DA = 86-2(AC+BD)
= 86-2×2×13
即矩形ABCD的周长等于34cm.
= 34cm
即 AB+BC+CD+DA+2(AC+BD) =86
A
B
C
D
O
10.如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值.
解:连接OP.
∵四边形ABCD是矩形,
∴∠DAB=90°,OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC=????????S矩形ABCD=????????×6×8=12.
在Rt△BAD中,由勾股定理得BD=10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴????????AO·PE+????????DO·PF=12,即5PE+5PF=24,
∴PE+PF=????????????.
?
A
B
C
D
O
P
E
F
当堂检测
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
