18.1.1.1平行四边形的边、角的特征 课件(共30张PPT)-2023-2024学年八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 18.1.1.1平行四边形的边、角的特征 课件(共30张PPT)-2023-2024学年八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 50.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
18.1.1.1
平行四边形的
边、角的特征
情景引入
新知探究
思考:
用两个全等的三角形纸片可以拼出几种形状不同的四边形?
新知探究
新知探究
观察图形,说出下列图形边的位置有什么特征?
思考:
两组对边不平行
新知探究
观察图形,说出下列图形边的位置有什么特征?
思考:
两组对边分别平行
新知探究
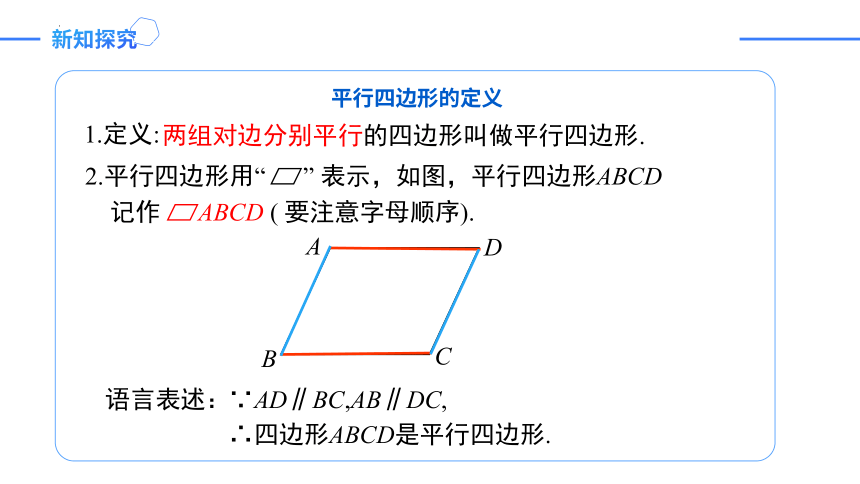
平行四边形的定义
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形用“ ” 表示,如图,平行四边形ABCD
记作 ABCD ( 要注意字母顺序).
1.定义:
A
B
D
C
语言表述:
∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
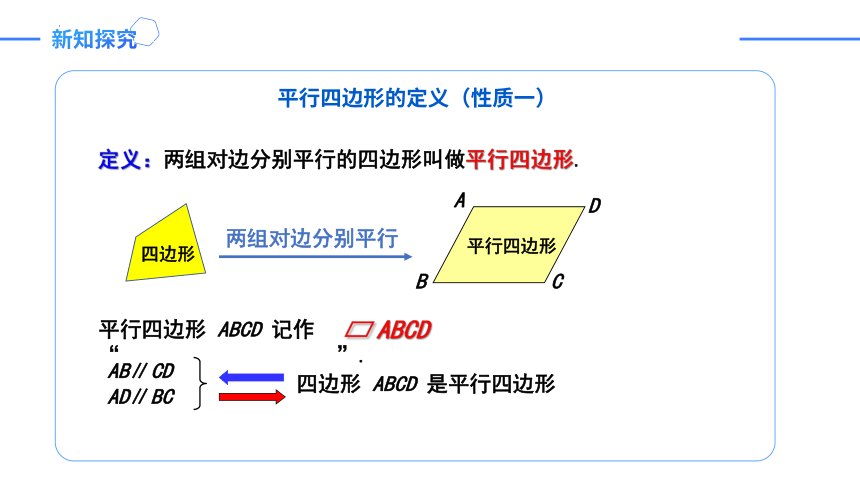
平行四边形的定义(性质一)
新知探究
定义:两组对边分别平行的四边形叫做平行四边形.
四边形
A
B
C
D
平行四边形
两组对边分别平行
平行四边形 ABCD 记作“ ”.
ABCD
四边形 ABCD 是平行四边形
AB∥CD
AD∥BC
典例精析
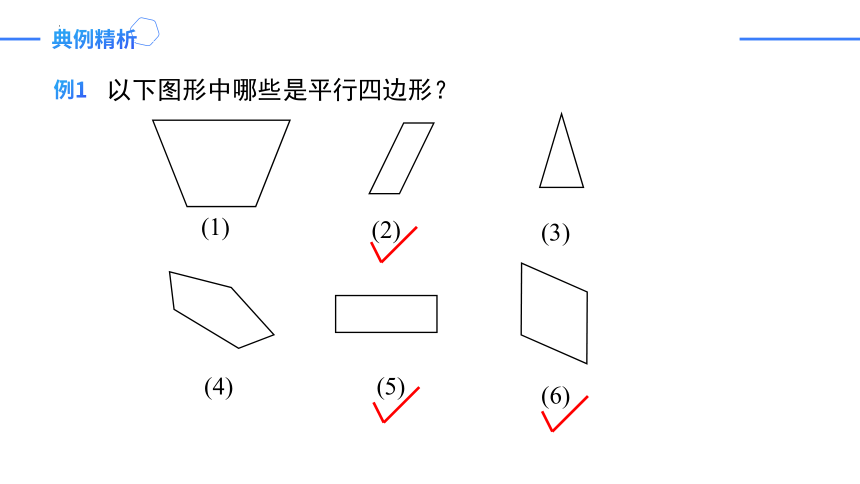
例1
以下图形中哪些是平行四边形?
(2)
(3)
(1)
(4)
(5)
(6)
典例精析
例2
如图,DC∥GH ∥ AB∥PQ,DA∥ EF∥ CB,图中的
平行四边形有多少个?将它们表示出来.
D
A
B
C
H
G
F
E
解:∵DC∥GH ∥ AB,
DA∥ EF∥ CB,
∴根据平行四边形的定义可以判定图中共有18个平行四边形,即
K
M
P
Q
AEGK, GKMP, PMFD, EBHK, KHQM,
MQCF, AEKG, GKFD, EBHK, KHCF,
ABHG, GNQP, PQCD, AEFD, EBCF,
ABQP, GHCD, ABCD.
新知探究
思考:
研究等腰三角形的性质是从哪些方面考虑的?
边和角
1.小组合作:利用学具探究平行四边形对边的数量关系和对角的数量关系.
探究:
2.汇报结论:展示实验过程,相互补充探究出的结论.
3.说理验证:利用所学几何知识通过说理能验证你的结论.
那么研究平行四边形首先可以从哪些方面考虑?
新知探究
平行四边形的性质二
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
A
B
C
D
新知探究
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA,
∴AD=BC,AB=CD,∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
归纳总结
新知探究
1.有关四边形的问题常常转化为三角形问题解决;
2.平行四边形的一条对角线把平行四边形分成两个全等的三角形.
A
B
C
D
转化思想:
四边形问题
转化
三角形问题
新知探究
A
B
C
D
法二:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
已知:四边形ABCD是平行四边形.
求证:∠BAD=∠BCD,∠ABC=∠ADC.
典例精析
例3
如图,在□ABCD中
(1)若∠A =130°,则∠B =_____ ,∠C =_____ , ∠D=_____。
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,
则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
典例精析
例4
如图,四边形 ABCD 和 BCEF 均为平行四边形,
AD = 2 cm,∠A = 65°,∠E = 33°,求 EF 和∠BGC.
∵ 四边形 ABCD 是平行四边形,
∴ AD = BC = 2 cm,∠1=∠A = 65°.
∵ 四边形 BCEF是平行四边形,
∴ EF = BC = 2 cm ,∠2 =∠E = 33°.
∴ 在△BGC中,∠BGC = 180°-∠1 -∠2 = 82°.
解
典例精析
例5
如图,在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
平面几何三要素:知二推一
等腰三角形
角的平分线
平行线
典例精析
例6
如图,□ ABCD 的一个外角为 38°,求∠A,∠B, ∠BCD,∠D 的度数.
解: ∵∠DCE = 38°
四边形ABCD为平行四边形,∴∠BCD=∠A=180°-38°=142°
∴∠B=∠D=38°
典例精析
例7
如图 , 在□ ABCD 中, AE⊥BC 于点 E , AF⊥DC交 DC 的延长线于点 F.若∠FCB = 30°, AE = 3,AF=5, 求 □ ABCD 的周长.
解: 在□ ABCD 中, CD∥AB,
∴∠B = ∠FCB = 30°.
又∵AE⊥BC , ∴在 Rt△ABE 中, AB=2AE=6.
又∵ ∠B = ∠D , AF⊥DF ,
∴ 在Rt△AFD 中, AD = 2AF=10.
∴ □ ABCD 的周长为 2(AD+AB)=32.
典例精析
例8
如图,直线 l1 与 l2 平行,AB,CD是 l1 与 l2 之间的任意两条平行线段. 试问:AB与CD是否相等?为什么?
∴AB=CD.
∵l1∥l2,AB∥CD,
∴四边形ABCD是平行四边形.
解
夹在两条平行线间的平行线段相等.
典例精析
例8
如图,直线 l1 与 l2 平行,AB,CD是 l1 与 l2 之间的任意两条平行线段. 试问:AB与CD是否相等?为什么?
仍有AB=CD.
两条平行线间的距离处处相等.
变式
其他条件不变,若AB⊥l1,CD⊥l2,
AB与CD是否相等?为什么?
典例精析
例9
(1)在□ABCD中,∠A=150°,AB=8cm,BC=10cm,则
S□ABCD= .
提示:过点A作AE⊥BC于E,然后利用勾股定理求出AE的值.
40cm2
(2)若点P是□ABCD上AD上任意一点,那么△PBC的面积是 .
20cm2
提示:△PBC与□ABCD是同底等高.
归纳总结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的平行线段相等
两条平行线间的距离
两组对角分别相等,邻角互补
当堂检测
1.如图, ABCD中,EF∥GH∥BC,MN∥AB,则图中平行四边形的个数是( )
A.13 B.14 C.15 D.18
D
2.如图,在□ ABCD 中,下列各式不一定正确的是( )
A.∠1+∠2=180°
B.∠2+∠3=180°
C.∠3+∠4=180°
D.∠2+∠4=180°
D
当堂检测
A 6cm B 12cm
C 4cm D 8cm
A
B
D
C
3.如图, 的周长是28cm,△ABC的周长是22cm,则AC的长为( )
ABCD
D
4.如图,在平行四边形ABCD中,∠BAD的平分线把BC边分成长度是6和8的两部分,则平行四边形ABCD的周长是( )
A.44 B.40
C.44或40 D.36
C
当堂检测
5.如图,在 ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2 B.3 C.4 D.6
C
6.直线a上有一点A,直线b上有一点B,且a∥b.点P在直线a,b之间,若PA=3,PB=4,则直线a,b之间的距离( )
A.等于7 B.小于7
C.不小于7 D.不大于7
D
当堂检测
7.如图,a∥b,若要使S△ABC=S△DEF,需增加条件( )
A.AB=DE
B.AC=DF
C.BC=EF
D.BE=AD
C
当堂检测
8. 如图,在 □ ABCD 中,∠ABC = 68°,BE 平分∠ABC,
交 AD 于点 E. AB = 2 cm,ED = 1 cm.
(1)求∠A,∠C,∠D 的度数;
(2)求 □ ABCD 的周长.
(1)解: ∠A = 112°;∠C = 112°; ∠D = 68° .
∴ AE = AB = 2 cm,
∴ AD = AE + ED = 2 + 1 = 3 (cm).
∴ □ ABCD 的周长
= 2 (AD+ AB) = 2×(3+2) = 10 (cm).
∠ABE =∠AEB.
(2)解:由已知可得
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
18.1.1.1
平行四边形的
边、角的特征
情景引入
新知探究
思考:
用两个全等的三角形纸片可以拼出几种形状不同的四边形?
新知探究
新知探究
观察图形,说出下列图形边的位置有什么特征?
思考:
两组对边不平行
新知探究
观察图形,说出下列图形边的位置有什么特征?
思考:
两组对边分别平行
新知探究
平行四边形的定义
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形用“ ” 表示,如图,平行四边形ABCD
记作 ABCD ( 要注意字母顺序).
1.定义:
A
B
D
C
语言表述:
∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
平行四边形的定义(性质一)
新知探究
定义:两组对边分别平行的四边形叫做平行四边形.
四边形
A
B
C
D
平行四边形
两组对边分别平行
平行四边形 ABCD 记作“ ”.
ABCD
四边形 ABCD 是平行四边形
AB∥CD
AD∥BC
典例精析
例1
以下图形中哪些是平行四边形?
(2)
(3)
(1)
(4)
(5)
(6)
典例精析
例2
如图,DC∥GH ∥ AB∥PQ,DA∥ EF∥ CB,图中的
平行四边形有多少个?将它们表示出来.
D
A
B
C
H
G
F
E
解:∵DC∥GH ∥ AB,
DA∥ EF∥ CB,
∴根据平行四边形的定义可以判定图中共有18个平行四边形,即
K
M
P
Q
AEGK, GKMP, PMFD, EBHK, KHQM,
MQCF, AEKG, GKFD, EBHK, KHCF,
ABHG, GNQP, PQCD, AEFD, EBCF,
ABQP, GHCD, ABCD.
新知探究
思考:
研究等腰三角形的性质是从哪些方面考虑的?
边和角
1.小组合作:利用学具探究平行四边形对边的数量关系和对角的数量关系.
探究:
2.汇报结论:展示实验过程,相互补充探究出的结论.
3.说理验证:利用所学几何知识通过说理能验证你的结论.
那么研究平行四边形首先可以从哪些方面考虑?
新知探究
平行四边形的性质二
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
A
B
C
D
新知探究
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA,
∴AD=BC,AB=CD,∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
归纳总结
新知探究
1.有关四边形的问题常常转化为三角形问题解决;
2.平行四边形的一条对角线把平行四边形分成两个全等的三角形.
A
B
C
D
转化思想:
四边形问题
转化
三角形问题
新知探究
A
B
C
D
法二:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
已知:四边形ABCD是平行四边形.
求证:∠BAD=∠BCD,∠ABC=∠ADC.
典例精析
例3
如图,在□ABCD中
(1)若∠A =130°,则∠B =_____ ,∠C =_____ , ∠D=_____。
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,
则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
典例精析
例4
如图,四边形 ABCD 和 BCEF 均为平行四边形,
AD = 2 cm,∠A = 65°,∠E = 33°,求 EF 和∠BGC.
∵ 四边形 ABCD 是平行四边形,
∴ AD = BC = 2 cm,∠1=∠A = 65°.
∵ 四边形 BCEF是平行四边形,
∴ EF = BC = 2 cm ,∠2 =∠E = 33°.
∴ 在△BGC中,∠BGC = 180°-∠1 -∠2 = 82°.
解
典例精析
例5
如图,在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
平面几何三要素:知二推一
等腰三角形
角的平分线
平行线
典例精析
例6
如图,□ ABCD 的一个外角为 38°,求∠A,∠B, ∠BCD,∠D 的度数.
解: ∵∠DCE = 38°
四边形ABCD为平行四边形,∴∠BCD=∠A=180°-38°=142°
∴∠B=∠D=38°
典例精析
例7
如图 , 在□ ABCD 中, AE⊥BC 于点 E , AF⊥DC交 DC 的延长线于点 F.若∠FCB = 30°, AE = 3,AF=5, 求 □ ABCD 的周长.
解: 在□ ABCD 中, CD∥AB,
∴∠B = ∠FCB = 30°.
又∵AE⊥BC , ∴在 Rt△ABE 中, AB=2AE=6.
又∵ ∠B = ∠D , AF⊥DF ,
∴ 在Rt△AFD 中, AD = 2AF=10.
∴ □ ABCD 的周长为 2(AD+AB)=32.
典例精析
例8
如图,直线 l1 与 l2 平行,AB,CD是 l1 与 l2 之间的任意两条平行线段. 试问:AB与CD是否相等?为什么?
∴AB=CD.
∵l1∥l2,AB∥CD,
∴四边形ABCD是平行四边形.
解
夹在两条平行线间的平行线段相等.
典例精析
例8
如图,直线 l1 与 l2 平行,AB,CD是 l1 与 l2 之间的任意两条平行线段. 试问:AB与CD是否相等?为什么?
仍有AB=CD.
两条平行线间的距离处处相等.
变式
其他条件不变,若AB⊥l1,CD⊥l2,
AB与CD是否相等?为什么?
典例精析
例9
(1)在□ABCD中,∠A=150°,AB=8cm,BC=10cm,则
S□ABCD= .
提示:过点A作AE⊥BC于E,然后利用勾股定理求出AE的值.
40cm2
(2)若点P是□ABCD上AD上任意一点,那么△PBC的面积是 .
20cm2
提示:△PBC与□ABCD是同底等高.
归纳总结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的平行线段相等
两条平行线间的距离
两组对角分别相等,邻角互补
当堂检测
1.如图, ABCD中,EF∥GH∥BC,MN∥AB,则图中平行四边形的个数是( )
A.13 B.14 C.15 D.18
D
2.如图,在□ ABCD 中,下列各式不一定正确的是( )
A.∠1+∠2=180°
B.∠2+∠3=180°
C.∠3+∠4=180°
D.∠2+∠4=180°
D
当堂检测
A 6cm B 12cm
C 4cm D 8cm
A
B
D
C
3.如图, 的周长是28cm,△ABC的周长是22cm,则AC的长为( )
ABCD
D
4.如图,在平行四边形ABCD中,∠BAD的平分线把BC边分成长度是6和8的两部分,则平行四边形ABCD的周长是( )
A.44 B.40
C.44或40 D.36
C
当堂检测
5.如图,在 ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2 B.3 C.4 D.6
C
6.直线a上有一点A,直线b上有一点B,且a∥b.点P在直线a,b之间,若PA=3,PB=4,则直线a,b之间的距离( )
A.等于7 B.小于7
C.不小于7 D.不大于7
D
当堂检测
7.如图,a∥b,若要使S△ABC=S△DEF,需增加条件( )
A.AB=DE
B.AC=DF
C.BC=EF
D.BE=AD
C
当堂检测
8. 如图,在 □ ABCD 中,∠ABC = 68°,BE 平分∠ABC,
交 AD 于点 E. AB = 2 cm,ED = 1 cm.
(1)求∠A,∠C,∠D 的度数;
(2)求 □ ABCD 的周长.
(1)解: ∠A = 112°;∠C = 112°; ∠D = 68° .
∴ AE = AB = 2 cm,
∴ AD = AE + ED = 2 + 1 = 3 (cm).
∴ □ ABCD 的周长
= 2 (AD+ AB) = 2×(3+2) = 10 (cm).
∠ABE =∠AEB.
(2)解:由已知可得
