第17章 勾股定理复盘提升 单元复习课件(共26张PPT)-2023-2024学年八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 第17章 勾股定理复盘提升 单元复习课件(共26张PPT)-2023-2024学年八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 32.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第17章
勾股定理
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
单元复盘提升
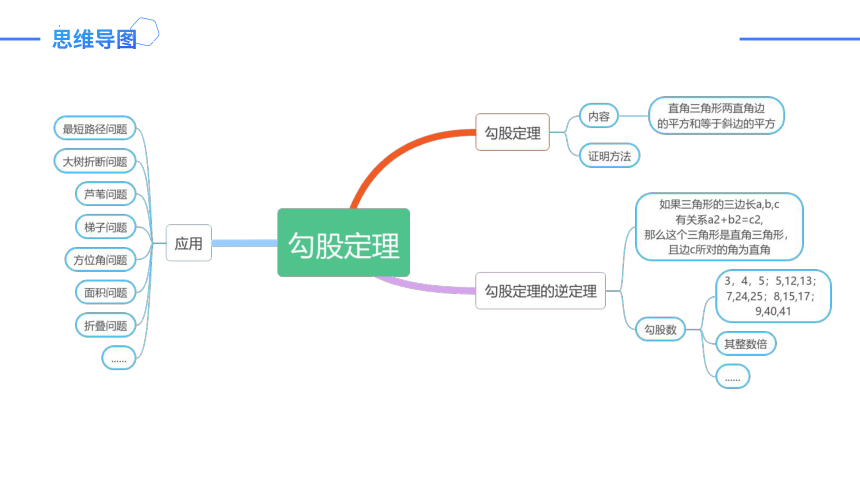
思维导图
知识串讲
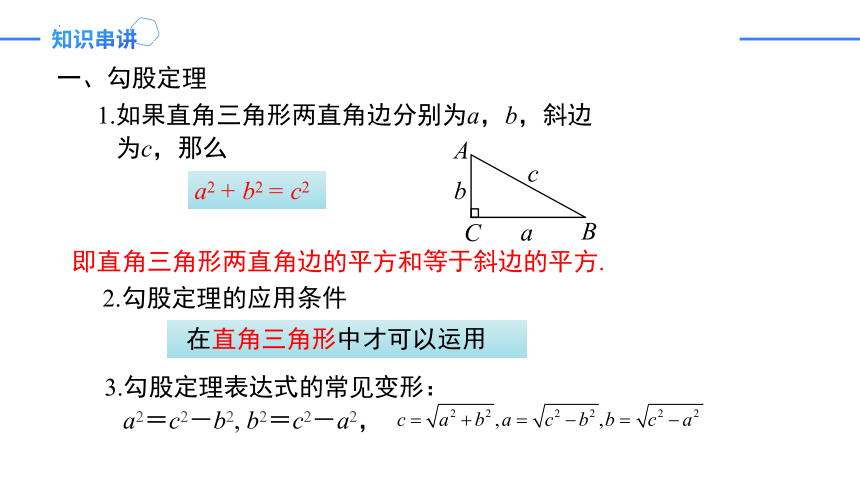
1.如果直角三角形两直角边分别为a,b,斜边
为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
2.勾股定理的应用条件
一、勾股定理
3.勾股定理表达式的常见变形:
a2=c2-b2, b2=c2-a2,
A
B
C
c
a
b
知识串讲
二、勾股定理的逆定理
1.勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
2.勾股数
3.原命题与逆命题
如果两个命题的题设、结论正好相反,那么把其中一个
叫做原命题,另一个叫做它的逆命题.
A
B
C
c
a
b
考点梳理
考点一:勾股定理及其应用
例1
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)已知a=7,b=24,求c;
(2)已知c=61,b=60,求a;
(3)已知a:b=3:4,c=25,求b.
考点梳理
例1
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)已知a=7,b=24,求c;
(2)已知c=61,b=60,求a;
(3)已知a:b=3:4,c=25,求b.
考点梳理
例2
如图,在△ABC中,AB=17,BC=9,AC=10AD⊥BC于D.试求△ABC的面积.
解:在Rt△ABD和Rt△ACD中,
AB2-BD2=AD2,AC2-CD2=AD2,
设DC=x,则BD=9+x,
故172-(9+x)2=102-x2,
解得x=6.
∴AD2= AC2 CD2 = 64,∴AD=8.
∴S△ABC= ×9×8=36.
考点梳理
例3
如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长2.5米,顶端A在AC上运动,量得滑杆下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑杆顶端A下滑多少米?
A
E
C
B
D
解:设AE的长为x 米,依题意
得CE=AC - x ,∵AB=DE=2.5,BC=1.5,
∠C=90°,∴AC=2.∵BD=0.5,∴AC=2.
∴在Rt△ECD中,CE=1.5.
∴2- x =1.5, x =0.5. 即AE=0.5 .
答:梯子下滑0.5米.
考点梳理
例4
如图,在△ABC中,AB>AC,AD是BC边上的高,将△ADC
沿AD所在直线翻折,使点C落在BC边上的点E处.
(1)若AB=20,AC=13,CD=5,求△ABC的面积;
(2)求证:AB2-AC2=BE·BC.
解:(1)∵AD是BC边上的高
∴∠ADB=∠ADC=90°
在Rt△ADC中,AC=13,CD=5,
∴AD2=AC2-CD2=144,∴AD=12.
在Rt△ADB中,AB=20,AD=12,
∴BD2=AB2-AD2=256,∴BD=16
∴BC=BD+CD=21,
∴S△ABC=0.5×BC×AD=126.
考点梳理
例4
(2)求证:AB2-AC2=BE·BC.
(2)证明:由题意得AC=AE,DC=DE,
在Rt△ADC中,由勾股定理得
AC2=AD2+CD2
在Rt△ADB中,由勾股定理得
BD2=AB2-AD2
∴AB2-AC2=AB2-(AD2+CD2)
=AB2-AD2-CD2
=BD2-DE2
=(BD-DE)(BD+DE)
∵BE=BD-DE,BC=BD+CD=BD+DE
∴AB2-AC2=BE·BC
考点梳理
例5
已知Rt△ABC中,∠C=90°,若a +b=14cm,c=10cm,求△ABC的面积.
解:∵a+b=14,
∴(a+b)2=196.
又∵a2+b2=c2=100,
∴2ab=196-(a2+b2)=96,
∴ ab=24,
即△ABC的面积为24.
刻意练习
练1
在Rt△ABC中,∠C=90°,周长为60,斜边与一条直角边之比为13:5,则这个直角三角形三边的长度分别是( )A.25,23,12 B.13,12,5 C.10,8,6 D.26,24,10
练2
如图,两个较大正方形的面积分别是255,289,
则字母A所代表的正方形的边长是 .
练3
8.若等边△ABC的边长为2cm,那么△ABC的面积
为( ).
A. B. C. D.
A
刻意练习
练4
如果Rt△的两直角边长分别为n2-1,2n(n>1), 那么它的斜边长是( )
A、2n B、n+1 C、n2-1 D、n2+1
已知Rt△ABC中,∠C=90°,若a+b=14cm, c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm2
等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56 B、48 C、40 D、32
D
A
B
练5
练6
考点梳理
考点二:勾股定理的逆定理及其应用
例6
已知a,b,c是△ABC的三边长,且满足关系
请判断△ABC的形状.
考点梳理
例7
如图,在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C的关系,并加以证明.
解:猜想∠A+∠C=180°.
连接AC.
∵∠ABC=90°,
∴在Rt△ABC中,由勾股定理得
∵AD2+DC2=625=252=AC2,
∴△ADC是直角三角形,且∠D=90°,
∵∠DAB+∠B+∠BCD+∠D=360°,
∴∠DAB+∠BCD=180°,
即∠A+∠C=180°.
刻意练习
练7
下列各组数中,不能作为直角三角形三边长的是( )
A.0.3,0.4,0.5 B.8.9.10 C.7.24.25 D.9.12.15
根据下列条件,能判定一个三角形是直角三角形的是( )
A.三条边的长度之比是2:3:4
B.三个内角的度数之比是1:1:2
C.三条边的边长分别是
D.三条边的边长分别是12,15,20
在△ABC中,a=3,b=7,c2=58,则S△ABC= .
练8
练9
刻意练习
练10
如图,厂房屋顶的人字架是等腰三角形,AB=AC,AD⊥BC,若跨度BC=16m,上弦长AB=10m,求中柱AD的长.
解:∵AB=AC,AD⊥BC,BC=16m,
∴BC=CD= BC=8m,∠ADB=90°,
∴AD= ,
即中柱AD的长为6m.
考点梳理
考点三:勾股定理的应用
例8
如图,一个圆桶的底面直径为16cm,高为18cm,一只小虫从下底面点A处爬到上底面点B处,求小虫所爬的最短路径长.
考点梳理
例9
如图,折叠长方形的纸片ABCD,使点B落在AD上一点E处,折痕的两端点分别在AB,BC上(含端点),且AB=6,BC=10.设AE=x,求x的取值范围.
考点梳理
例10
如图,正方形ABCD的边长是9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为CH,若BE:EC=2:1,求线段CH的长.
解:由题意得EC=3,
设CH=x,则DH=9-x,
由折叠可知EH=DH=9-x,
在Rt△ECH中,∠C=90°,
∴EC2+CH2=EH2,
即32+x2=(9-x)2,
解得x=4,
∴CH=4.
考点梳理
例11
1000
600
800
B
C
A
公园半径为400m
点A是一个圆形森林公园的中心,在森林公园附近有B、C 两个村庄,现要在 B、C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得AB=600m,AC=800m,问此公路是否会穿过该森林公园
考点梳理
D
过点A作AD⊥BC交BC于点D.
∵ AB·AC= AD·BC.
∴这条公路不会穿过自然保护区.
∴AD=480
解:在△ABC中
∵AB2+AC2=6002+8002=10002=BC2.
∴△ABC为直角三角形,∠BAC=90°
∵480>400
1000
600
800
A
B
C
刻意练习
练11
如图,在Rt△ABC中,∠A=90°,
D是BC的中点,ED⊥BC于点D,
交AB于点E,连接CE.若AE=3,BE=5,
则边AC的长为 .
4
如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B’处,点A落在点A’处,若AE=3,AB=4,则BF的长为 .
5
练12
刻意练习
练13
如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要( )
A.8 cm B.10 cm C.12 cm D.15 cm
B
小亮想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多2m,当他把绳子的下端拉开8m后,下端刚好接触到地面,则学校旗杆的高度为( )
A.10m B.12m C.15m D.18m
C
练14
刻意练习
练15
如图,四边形ABCD是长方形,把△ACD沿AC折叠到△ACD’,AD’与BC交于点E,若AD=4,DC=3,求BE的长.
解:∵四边形ABCD为长方形
∴AB=CD=3,BC=AD=4,AD∥BC,∠B=90°,
∴∠DAC=∠ACB,由折叠可知 ,∠DAC=∠D’AC
∴∠D’AC=∠ACB∴AE=EC
设BE=x,则EC=4-x=AE,在Rt△ABE中,AB2+BE2=AE2,即32+x2=(4-x)2,解得x=7/8
即BE=7/8.
第17章
勾股定理
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
单元复盘提升
思维导图
知识串讲
1.如果直角三角形两直角边分别为a,b,斜边
为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
2.勾股定理的应用条件
一、勾股定理
3.勾股定理表达式的常见变形:
a2=c2-b2, b2=c2-a2,
A
B
C
c
a
b
知识串讲
二、勾股定理的逆定理
1.勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
2.勾股数
3.原命题与逆命题
如果两个命题的题设、结论正好相反,那么把其中一个
叫做原命题,另一个叫做它的逆命题.
A
B
C
c
a
b
考点梳理
考点一:勾股定理及其应用
例1
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)已知a=7,b=24,求c;
(2)已知c=61,b=60,求a;
(3)已知a:b=3:4,c=25,求b.
考点梳理
例1
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)已知a=7,b=24,求c;
(2)已知c=61,b=60,求a;
(3)已知a:b=3:4,c=25,求b.
考点梳理
例2
如图,在△ABC中,AB=17,BC=9,AC=10AD⊥BC于D.试求△ABC的面积.
解:在Rt△ABD和Rt△ACD中,
AB2-BD2=AD2,AC2-CD2=AD2,
设DC=x,则BD=9+x,
故172-(9+x)2=102-x2,
解得x=6.
∴AD2= AC2 CD2 = 64,∴AD=8.
∴S△ABC= ×9×8=36.
考点梳理
例3
如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长2.5米,顶端A在AC上运动,量得滑杆下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑杆顶端A下滑多少米?
A
E
C
B
D
解:设AE的长为x 米,依题意
得CE=AC - x ,∵AB=DE=2.5,BC=1.5,
∠C=90°,∴AC=2.∵BD=0.5,∴AC=2.
∴在Rt△ECD中,CE=1.5.
∴2- x =1.5, x =0.5. 即AE=0.5 .
答:梯子下滑0.5米.
考点梳理
例4
如图,在△ABC中,AB>AC,AD是BC边上的高,将△ADC
沿AD所在直线翻折,使点C落在BC边上的点E处.
(1)若AB=20,AC=13,CD=5,求△ABC的面积;
(2)求证:AB2-AC2=BE·BC.
解:(1)∵AD是BC边上的高
∴∠ADB=∠ADC=90°
在Rt△ADC中,AC=13,CD=5,
∴AD2=AC2-CD2=144,∴AD=12.
在Rt△ADB中,AB=20,AD=12,
∴BD2=AB2-AD2=256,∴BD=16
∴BC=BD+CD=21,
∴S△ABC=0.5×BC×AD=126.
考点梳理
例4
(2)求证:AB2-AC2=BE·BC.
(2)证明:由题意得AC=AE,DC=DE,
在Rt△ADC中,由勾股定理得
AC2=AD2+CD2
在Rt△ADB中,由勾股定理得
BD2=AB2-AD2
∴AB2-AC2=AB2-(AD2+CD2)
=AB2-AD2-CD2
=BD2-DE2
=(BD-DE)(BD+DE)
∵BE=BD-DE,BC=BD+CD=BD+DE
∴AB2-AC2=BE·BC
考点梳理
例5
已知Rt△ABC中,∠C=90°,若a +b=14cm,c=10cm,求△ABC的面积.
解:∵a+b=14,
∴(a+b)2=196.
又∵a2+b2=c2=100,
∴2ab=196-(a2+b2)=96,
∴ ab=24,
即△ABC的面积为24.
刻意练习
练1
在Rt△ABC中,∠C=90°,周长为60,斜边与一条直角边之比为13:5,则这个直角三角形三边的长度分别是( )A.25,23,12 B.13,12,5 C.10,8,6 D.26,24,10
练2
如图,两个较大正方形的面积分别是255,289,
则字母A所代表的正方形的边长是 .
练3
8.若等边△ABC的边长为2cm,那么△ABC的面积
为( ).
A. B. C. D.
A
刻意练习
练4
如果Rt△的两直角边长分别为n2-1,2n(n>1), 那么它的斜边长是( )
A、2n B、n+1 C、n2-1 D、n2+1
已知Rt△ABC中,∠C=90°,若a+b=14cm, c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm2
等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56 B、48 C、40 D、32
D
A
B
练5
练6
考点梳理
考点二:勾股定理的逆定理及其应用
例6
已知a,b,c是△ABC的三边长,且满足关系
请判断△ABC的形状.
考点梳理
例7
如图,在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C的关系,并加以证明.
解:猜想∠A+∠C=180°.
连接AC.
∵∠ABC=90°,
∴在Rt△ABC中,由勾股定理得
∵AD2+DC2=625=252=AC2,
∴△ADC是直角三角形,且∠D=90°,
∵∠DAB+∠B+∠BCD+∠D=360°,
∴∠DAB+∠BCD=180°,
即∠A+∠C=180°.
刻意练习
练7
下列各组数中,不能作为直角三角形三边长的是( )
A.0.3,0.4,0.5 B.8.9.10 C.7.24.25 D.9.12.15
根据下列条件,能判定一个三角形是直角三角形的是( )
A.三条边的长度之比是2:3:4
B.三个内角的度数之比是1:1:2
C.三条边的边长分别是
D.三条边的边长分别是12,15,20
在△ABC中,a=3,b=7,c2=58,则S△ABC= .
练8
练9
刻意练习
练10
如图,厂房屋顶的人字架是等腰三角形,AB=AC,AD⊥BC,若跨度BC=16m,上弦长AB=10m,求中柱AD的长.
解:∵AB=AC,AD⊥BC,BC=16m,
∴BC=CD= BC=8m,∠ADB=90°,
∴AD= ,
即中柱AD的长为6m.
考点梳理
考点三:勾股定理的应用
例8
如图,一个圆桶的底面直径为16cm,高为18cm,一只小虫从下底面点A处爬到上底面点B处,求小虫所爬的最短路径长.
考点梳理
例9
如图,折叠长方形的纸片ABCD,使点B落在AD上一点E处,折痕的两端点分别在AB,BC上(含端点),且AB=6,BC=10.设AE=x,求x的取值范围.
考点梳理
例10
如图,正方形ABCD的边长是9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为CH,若BE:EC=2:1,求线段CH的长.
解:由题意得EC=3,
设CH=x,则DH=9-x,
由折叠可知EH=DH=9-x,
在Rt△ECH中,∠C=90°,
∴EC2+CH2=EH2,
即32+x2=(9-x)2,
解得x=4,
∴CH=4.
考点梳理
例11
1000
600
800
B
C
A
公园半径为400m
点A是一个圆形森林公园的中心,在森林公园附近有B、C 两个村庄,现要在 B、C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得AB=600m,AC=800m,问此公路是否会穿过该森林公园
考点梳理
D
过点A作AD⊥BC交BC于点D.
∵ AB·AC= AD·BC.
∴这条公路不会穿过自然保护区.
∴AD=480
解:在△ABC中
∵AB2+AC2=6002+8002=10002=BC2.
∴△ABC为直角三角形,∠BAC=90°
∵480>400
1000
600
800
A
B
C
刻意练习
练11
如图,在Rt△ABC中,∠A=90°,
D是BC的中点,ED⊥BC于点D,
交AB于点E,连接CE.若AE=3,BE=5,
则边AC的长为 .
4
如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B’处,点A落在点A’处,若AE=3,AB=4,则BF的长为 .
5
练12
刻意练习
练13
如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要( )
A.8 cm B.10 cm C.12 cm D.15 cm
B
小亮想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多2m,当他把绳子的下端拉开8m后,下端刚好接触到地面,则学校旗杆的高度为( )
A.10m B.12m C.15m D.18m
C
练14
刻意练习
练15
如图,四边形ABCD是长方形,把△ACD沿AC折叠到△ACD’,AD’与BC交于点E,若AD=4,DC=3,求BE的长.
解:∵四边形ABCD为长方形
∴AB=CD=3,BC=AD=4,AD∥BC,∠B=90°,
∴∠DAC=∠ACB,由折叠可知 ,∠DAC=∠D’AC
∴∠D’AC=∠ACB∴AE=EC
设BE=x,则EC=4-x=AE,在Rt△ABE中,AB2+BE2=AE2,即32+x2=(4-x)2,解得x=7/8
即BE=7/8.
