汕头市经济特区某重点中学2023-2024学年度第二学期九年级数学科综合素质摸查(含答案)
文档属性
| 名称 | 汕头市经济特区某重点中学2023-2024学年度第二学期九年级数学科综合素质摸查(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 405.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 00:00:00 | ||
图片预览

文档简介
汕头市经济特区某重点中学2023-2024学年度第二学期九年级数学科综合素质摸查
一、单选题(本大题10小题,每小题3分,共30分)
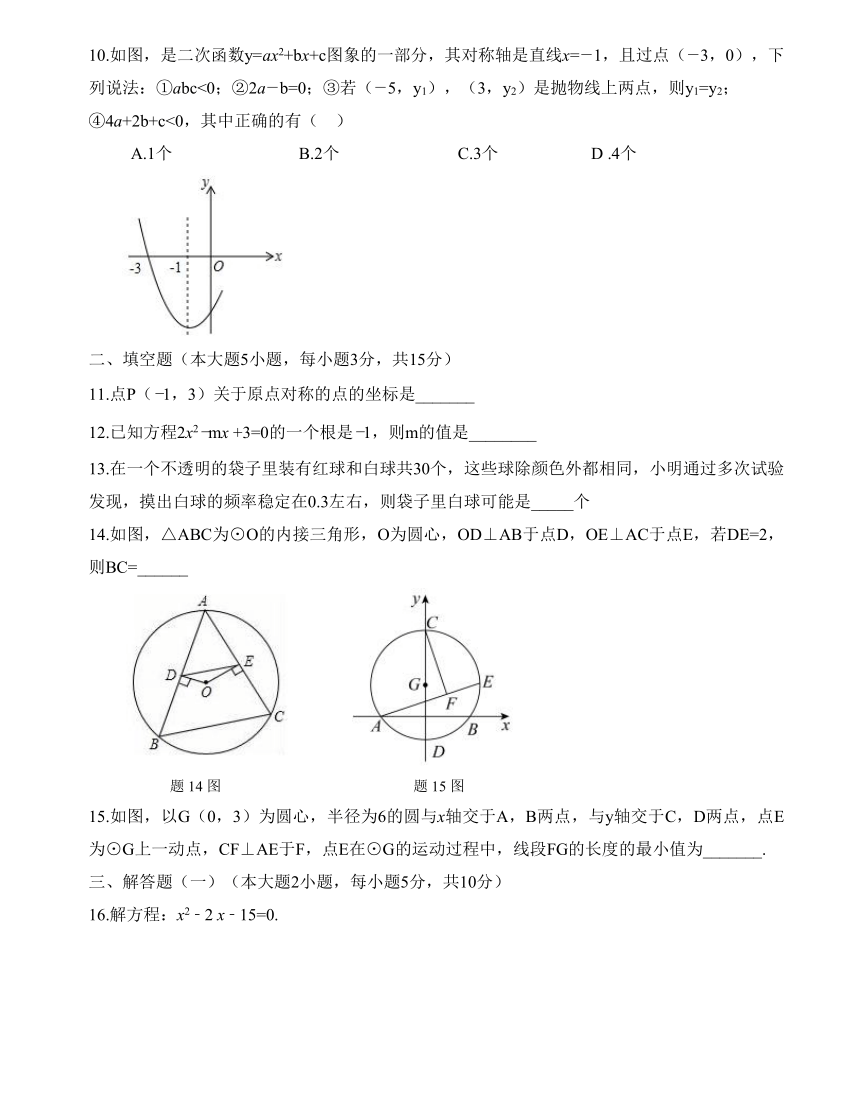
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A . B . C. D.
2.抛物线y=( x+1 )2+2的对称轴是( )
A.直线x =1 B.直线x =-1 C.直线y=-1 D.直线y=1
3.用配方法解一元二次方程x2+4x +1=0,下列变形正确的是( )
A. ( x +2)2=3 B. ( x +4)2=15 C. ( x +2)2=15 D. ( x-2)2-3=0
4.抛物线y= x2向左平移1个单位,再向上平移2个单位后,所得抛物线的表达式是( )
A.y=( x +1)2-2 В.y=( x +1)2+2 C.y=( x -1)2-2 D.y=( x -1)2+2
5.如图,AB是⊙O的弦,OC⊥AB于点D,交⊙O于点C,若半径为5,OD=3,则弦AB的长为( )
A.5 B.6 C.7 D.8
6.设x1,x2是一元二次方程x2-2x-1=0的两根,则+=( )。
A . B. C.2 D. -2
7.点A(-2,m),B(3,n)是反比例函数y=的图象上两点,则m、n大小关系为( )
A.mn D.无法确定
8.已知圆心角为120°的扇形的弧长为6π,该扇形的面积为( )
A.18π B.27π C.36π D.54π
9.在同一坐标系中,一次函数y=ax+k与二次函数y=kx2+a的图象可能是( )
A B C D
10.如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴是直线x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③若(-5,y1),(3,y2)是抛物线上两点,则y1=y2;
④4a+2b+c<0,其中正确的有( )
A.1个 B.2个 C.3个 D .4个
二、填空题(本大题5小题,每小题3分,共15分)
11.点P(-1,3)关于原点对称的点的坐标是_______
12.已知方程2x2-mx +3=0的一个根是-1,则m的值是________
13.在一个不透明的袋子里装有红球和白球共30个,这些球除颜色外都相同,小明通过多次试验发现,摸出白球的频率稳定在0.3左右,则袋子里白球可能是_____个
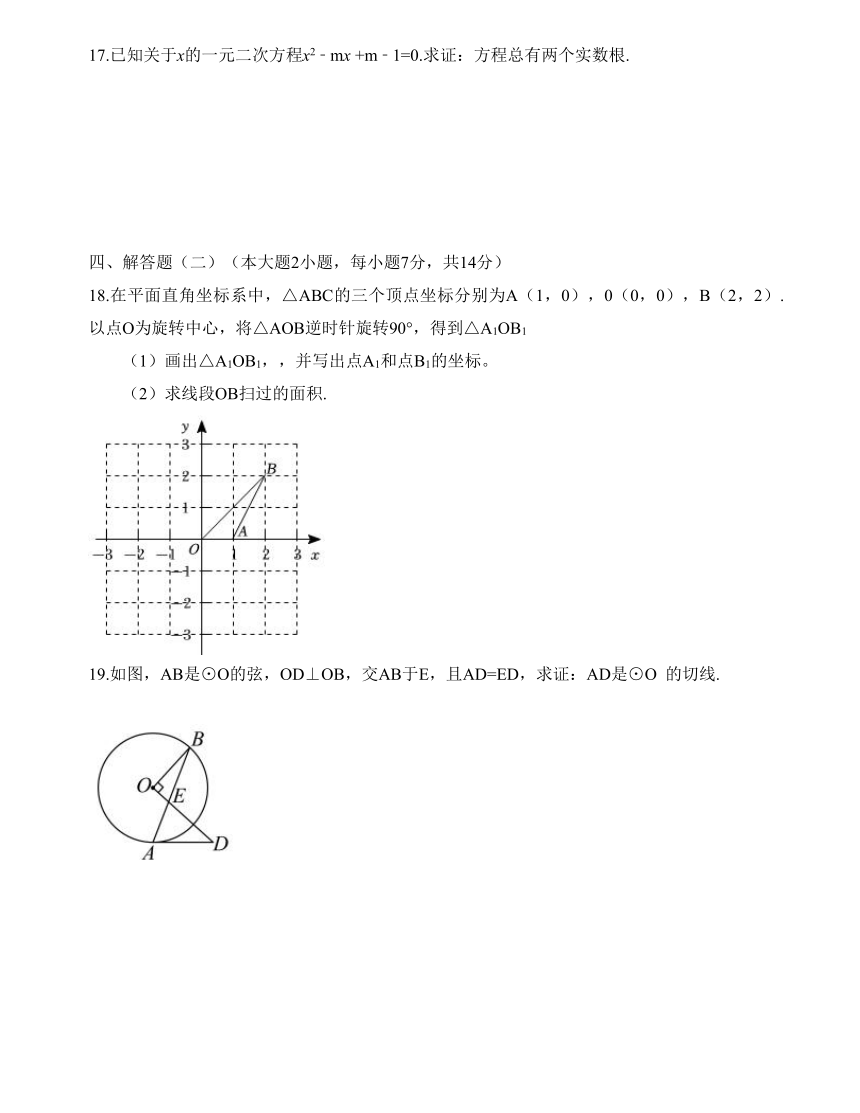
14.如图,△ABC为⊙O的内接三角形,O为圆心,OD⊥AB于点D,OE⊥AC于点E,若DE=2,则BC=______
题14图 题15图
15.如图,以G(0,3)为圆心,半径为6的圆与x轴交于A,B两点,与y轴交于C,D两点,点E为⊙G上一动点,CF⊥AE于F,点E在⊙G的运动过程中,线段FG的长度的最小值为_______.
三、解答题(一)(本大题2小题,每小题5分,共10分)
16.解方程:x2﹣2 x﹣15=0.
17.已知关于x的一元二次方程x2﹣mx +m﹣1=0.求证:方程总有两个实数根.
四、解答题(二)(本大题2小题,每小题7分,共14分)
18.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,0),0(0,0),B(2,2).以点O为旋转中心,将△AOB逆时针旋转90°,得到△A1OB1
(1)画出△A1OB1,,并写出点A1和点B1的坐标。
(2)求线段OB扫过的面积.
19.如图,AB是⊙O的弦,OD⊥OB,交AB于E,且AD=ED,求证:AD是⊙O 的切线.
五、解答题(三)(本大题3小题,每小题9分,共27分)
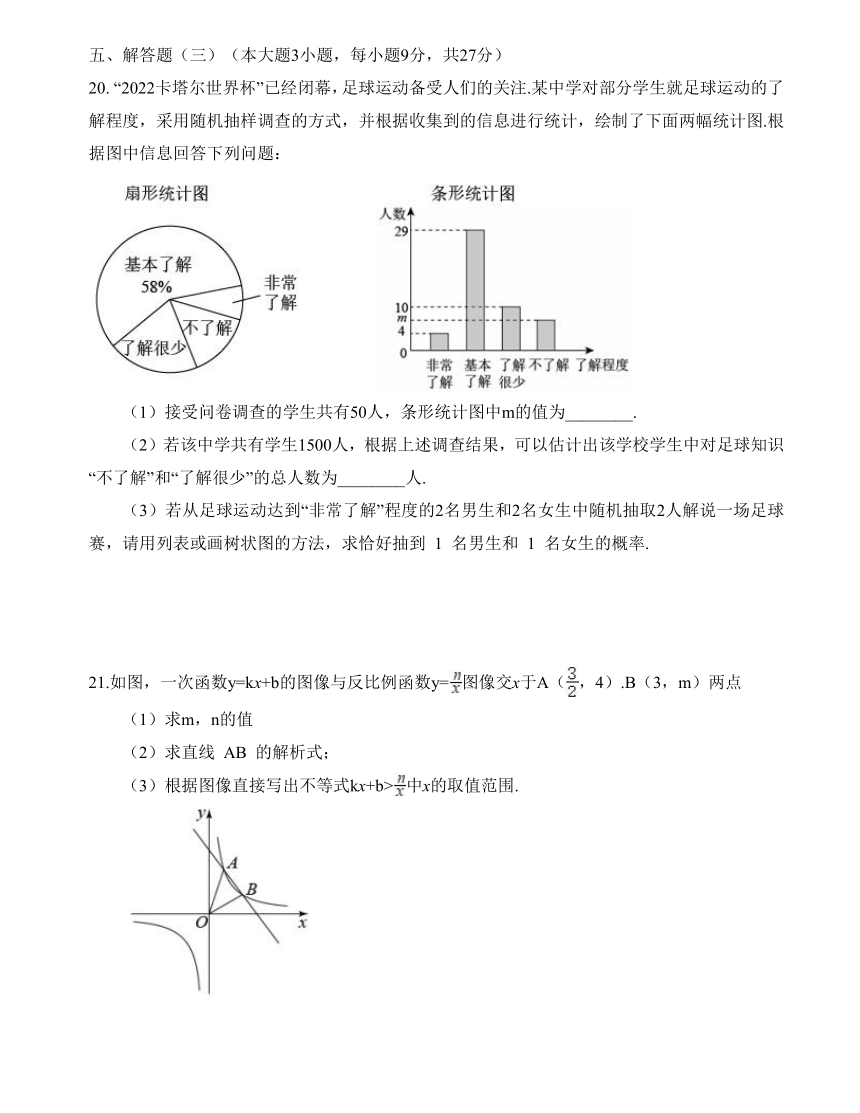
20. “2022卡塔尔世界杯”已经闭幕,足球运动备受人们的关注.某中学对部分学生就足球运动的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅统计图.根据图中信息回答下列问题:
(1)接受问卷调查的学生共有50人,条形统计图中m的值为________.
(2)若该中学共有学生1500人,根据上述调查结果,可以估计出该学校学生中对足球知识“不了解”和“了解很少”的总人数为________人.
(3)若从足球运动达到“非常了解”程度的2名男生和2名女生中随机抽取2人解说一场足球赛,请用列表或画树状图的方法,求恰好抽到 1 名男生和 1 名女生的概率.
21.如图,一次函数y=kx+b的图像与反比例函数y=图像交x于A(,4).B(3,m)两点
(1)求m,n的值
(2)求直线 AB 的解析式;
(3)根据图像直接写出不等式kx+b>中x的取值范围.
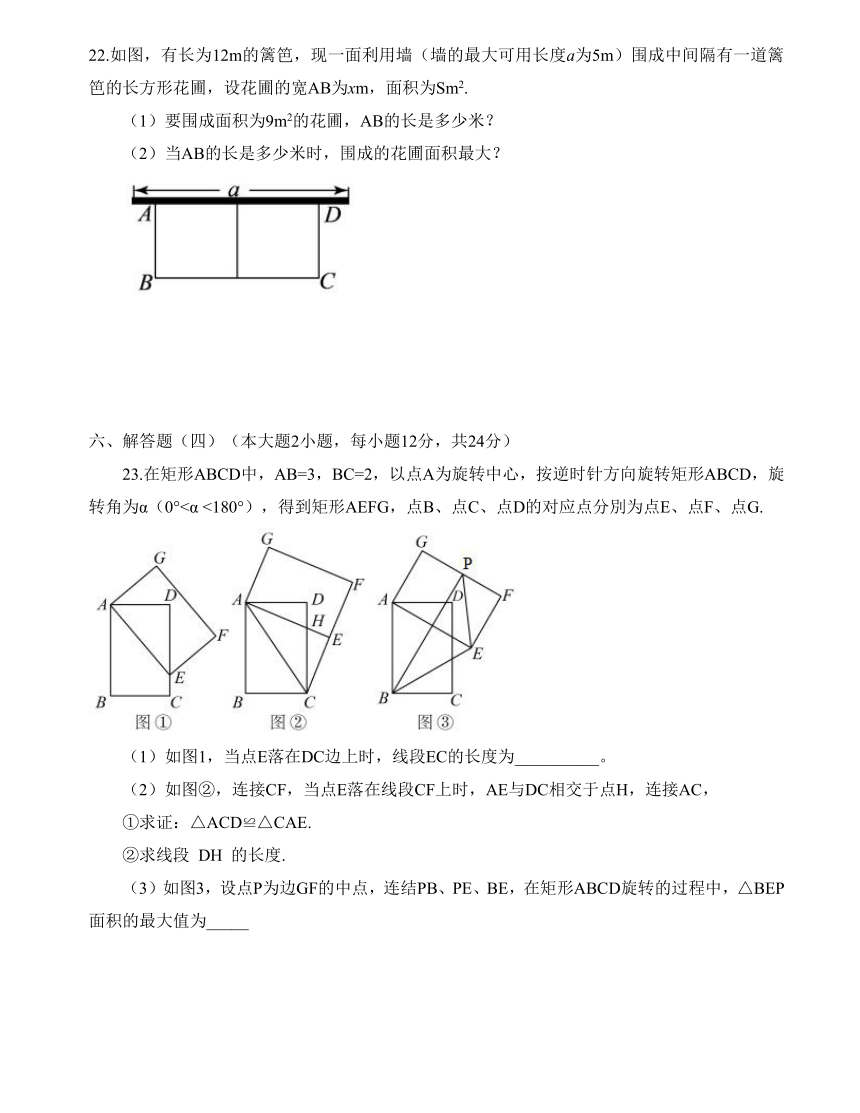
22.如图,有长为12m的篱笆,现一面利用墙(墙的最大可用长度a为5m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
(1)要围成面积为9m2的花圃,AB的长是多少米?
(2)当AB的长是多少米时,围成的花圃面积最大?
六、解答题(四)(本大题2小题,每小题12分,共24分)
23.在矩形ABCD中,AB=3,BC=2,以点A为旋转中心,按逆时针方向旋转矩形ABCD,旋转角为α(0°<α <180°),得到矩形AEFG,点B、点C、点D的对应点分別为点E、点F、点G.
(1)如图1,当点E落在DC边上时,线段EC的长度为__________。
(2)如图②,连接CF,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
①求证:△ACD≌△CAE.
②求线段 DH 的长度.
(3)如图3,设点P为边GF的中点,连结PB、PE、BE,在矩形ABCD旋转的过程中,△BEP 面积的最大值为_____
24.抛物线y=ax2+bx-4(a≠0)与x轴交于点A(-2,0)和B(4,0),与y轴交于点C,连接BC.点P是线段BC下方抛物线上的一个动点(不与点 B,C重合),过点P作y轴的平行线交BC于M,交x轴于 N,设点 P 的横坐标为t.
(1)求该抛物线的解析式:
(2)用关于t的代数式表示线段PM,求PM的最大值及此时点M的坐标:
(3)过点C作CH⊥PN于点H,S△BMN=9S△CHM,
①求点P的坐标:
②连接CP,在 y轴上是否存在点 Q,使得△CPQ为直角三角形,若存在,求出点 Q的坐标:若不存在,请说明理由.
一、单选题(本大题10小题,每小题3分,共30分)
1 2 3 4 5 6 7 8 9 10
B B A В. D D A B C C
二、填空题(本大题5小题,每小题3分,共15分)
11. (1,-3)
12. - 5
13. 9
14. 4
15. 3 -3
三、解答题(一)(本大题2小题,每小题5分,共10分)
16.解:原方程化为:
(x﹣5 ) (x +3) =0.
∴ x1=5,x2=﹣3
17.证明:∵Δ=(﹣m)2– 4(m–1)=(m–2)2 ≥0,
∴方程总有两个实数根.
四、解答题(二)(本大题2小题,每小题7分,共14分)
18.(1)画出△A1OB1,如图.
点A1(0,1),点B1(-2,2).
(2)∵ OB1 = OB =
∴扇形BOB1面积=
∴线段OB扫过的面积2π.
19. 证明:如图,连接OA
∵ OA=OB,AD=ED,
∴∠OBE= ∠OAE,∠AED= ∠EAD.
∵∠OEB= ∠AED,
∴∠OEB= ∠EAD,
∵OD⊥OB,
∴∠BOΕ = 90°,
∴∠OBE+∠OEB= 90°,
∴∠OAE+ ∠EAD= 90°,
∴∠OAD=90°,
又∵OA是⊙O的半径,
∴AD是⊙O的切线.
五、解答题(三)(本大题3小题,每小题9分,共27分)
20.(1)解:接受问卷调查的学生共有,29÷58%=50(人);
条形统计图中m的值为:50-4-29-10=7(人);
故答案为:50;7.
(2)解:达到“不了解”和“了解很少”程度的总人数为:
(10+7)÷50×1500=510(人);
故答案为:510.
(3)解:由题意列树状图:
由树状图可知,所有等可能的结果有12种,恰好抽到1名男生和1名女生的结果有8种,
∴恰好抽到1名男生和1名女生的概率为:
21.解:(1)∵一次函数y=kx+b的图像与反比例函数y=图像交x于(,4).B(3,m)
∴ n=×4= 6 .
y=
将B(3,m)代入y= y=
得m==2.
∴B(3,2);
(2)将A(,4),B(3,2)代入y=kx+b得:
解的:
∴直线AB的解析式为y=-x+6;
(3)∵A(,4),B(3,2)
结合函数图象可知:当x<0或
即不等式kx+b>的解集为:x<0或22. (1)解:由题意,AB=xm,则BC就为(12-3x)m.
∴S=x(12-3x)=-3x2+12x.
当S=9时,
-3x2+12x=9
解得x1= 1,x2 =3,
当x =1时,12-3x =12-3=9>5,不符合题意,舍去,
当x =3时,12-3x =12-9=3<5,符合题意,
∴要围成面积为9m2的花圃,AB的长是3米;
(2)由题意,可知:
∴< x≤4,
∵S=-3x2+12x =-3(x -2)2+12.
∵-3<0,抛物线开口向下,且对称轴为直线x=2
∴在∴当AB的长是米时,围成的花圃的面积最大
六、解答题(四)(本大题2小题,每小题12分,共24分)
23.解:(1)如图①中
∵ 四边形ABCD是矩形,
∴AB = CD = 3,BC = AD = 2,∠D = 90°,
∵矩形AEFG是由矩形ABCD旋转得到,
∴AE = AB = 3,
在RtΔADE中,DE = ,
∴CE =,
故答案为:.
(2)①证明:如图②中,
∵当点E落在线段CF上,
∴∠AEC = ∠ADC = 90,
在Rt△ADC和Rt△AEC中,
∴RtΔACD≌RtΔCAE(HL)
②如图②中,△ACD≌△CAE,
∴∠ACD =∠EAC
∴ AH = HC
设AH = HC =m
在RtΔADH中,:AD2 + DH2= AH2,
∴22 +(3-m)2 = m2
m=
∴DH =
故答案为:
(3)解:如图3中,连接PA,作AM ⊥PE于M.
当AM与AB共线,且BM=BA+AM时,△BPE面积最大
由题意:PF=PG=.
∵AG= EF =2,∠G= ∠F= 90°
∴PA=PE=.
∵S△APE=S矩形AGFE=PE·AM.
∴AM= = =
则S△BPE=PE·BM=××(3+)=
△PBE的面积的最大值为
故答案为:
24.解(1)∵抛物线y=ax2+bx-4(a≠0)与x轴交于点A(-2,0)和B(4,0)
∴
解得:
∴该抛物线的解析式为:y=x2-x-4
(2)在y=x2-x-4中,令x=0,得y=-4,
∴ C(0,-4),
设直线BC的解析式为y=kx+c,
∴
解得:
∴直线BC的解析式为y=x-4,
设P(t,t 2-t-4),则M(t, t-4),
∴PM= t-4-(t 2-t-4)=-(t-2)2+2
∵-<0.
∴当t =2时,PM取得最大值2,
此时点M的坐标为(2,-2);
(3)解:①如图1,
∵(t,t 2-t-4),M(t, t-4),N(t,0),B(4,0),C(0,-4),CH⊥PN.
∴BN=4-t,MN=4-t,CH = t,MH= t -4-(-4)= t
∵S△BMN=9S△CHM
∴(4-t)2=9×t 2
解得:t 1=1,t 2=-2,
∵点P是线段BC下方抛物线上的一个动点
∴0∴ t =1,
∴P(1,-)
②存在点Q使得△CPQ为直角三角形,设Q(0,m)
∵C(0,-4).P(1,-).
CP2=(1-0)2+(-+4)2=.
CQ2=(-4-m)2
PQ2= t 2+(--m)2,∠PCQ≠90°
当∠CQP=90°时,如图2,PQ⊥y轴
∴Q(0. -)
当∠CPQ=90°时,如图3,
在RtΔCPQ中,CP2+PQ2=CQ2
+ t 2+(--m)2 =(-4-m)2
解得:m=-
∴Q(0. -)
综上所述,点Q的坐标为(0、-)或(0. -).
一、单选题(本大题10小题,每小题3分,共30分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A . B . C. D.
2.抛物线y=( x+1 )2+2的对称轴是( )
A.直线x =1 B.直线x =-1 C.直线y=-1 D.直线y=1
3.用配方法解一元二次方程x2+4x +1=0,下列变形正确的是( )
A. ( x +2)2=3 B. ( x +4)2=15 C. ( x +2)2=15 D. ( x-2)2-3=0
4.抛物线y= x2向左平移1个单位,再向上平移2个单位后,所得抛物线的表达式是( )
A.y=( x +1)2-2 В.y=( x +1)2+2 C.y=( x -1)2-2 D.y=( x -1)2+2
5.如图,AB是⊙O的弦,OC⊥AB于点D,交⊙O于点C,若半径为5,OD=3,则弦AB的长为( )
A.5 B.6 C.7 D.8
6.设x1,x2是一元二次方程x2-2x-1=0的两根,则+=( )。
A . B. C.2 D. -2
7.点A(-2,m),B(3,n)是反比例函数y=的图象上两点,则m、n大小关系为( )
A.m
8.已知圆心角为120°的扇形的弧长为6π,该扇形的面积为( )
A.18π B.27π C.36π D.54π
9.在同一坐标系中,一次函数y=ax+k与二次函数y=kx2+a的图象可能是( )
A B C D
10.如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴是直线x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③若(-5,y1),(3,y2)是抛物线上两点,则y1=y2;
④4a+2b+c<0,其中正确的有( )
A.1个 B.2个 C.3个 D .4个
二、填空题(本大题5小题,每小题3分,共15分)
11.点P(-1,3)关于原点对称的点的坐标是_______
12.已知方程2x2-mx +3=0的一个根是-1,则m的值是________
13.在一个不透明的袋子里装有红球和白球共30个,这些球除颜色外都相同,小明通过多次试验发现,摸出白球的频率稳定在0.3左右,则袋子里白球可能是_____个
14.如图,△ABC为⊙O的内接三角形,O为圆心,OD⊥AB于点D,OE⊥AC于点E,若DE=2,则BC=______
题14图 题15图
15.如图,以G(0,3)为圆心,半径为6的圆与x轴交于A,B两点,与y轴交于C,D两点,点E为⊙G上一动点,CF⊥AE于F,点E在⊙G的运动过程中,线段FG的长度的最小值为_______.
三、解答题(一)(本大题2小题,每小题5分,共10分)
16.解方程:x2﹣2 x﹣15=0.
17.已知关于x的一元二次方程x2﹣mx +m﹣1=0.求证:方程总有两个实数根.
四、解答题(二)(本大题2小题,每小题7分,共14分)
18.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,0),0(0,0),B(2,2).以点O为旋转中心,将△AOB逆时针旋转90°,得到△A1OB1
(1)画出△A1OB1,,并写出点A1和点B1的坐标。
(2)求线段OB扫过的面积.
19.如图,AB是⊙O的弦,OD⊥OB,交AB于E,且AD=ED,求证:AD是⊙O 的切线.
五、解答题(三)(本大题3小题,每小题9分,共27分)
20. “2022卡塔尔世界杯”已经闭幕,足球运动备受人们的关注.某中学对部分学生就足球运动的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅统计图.根据图中信息回答下列问题:
(1)接受问卷调查的学生共有50人,条形统计图中m的值为________.
(2)若该中学共有学生1500人,根据上述调查结果,可以估计出该学校学生中对足球知识“不了解”和“了解很少”的总人数为________人.
(3)若从足球运动达到“非常了解”程度的2名男生和2名女生中随机抽取2人解说一场足球赛,请用列表或画树状图的方法,求恰好抽到 1 名男生和 1 名女生的概率.
21.如图,一次函数y=kx+b的图像与反比例函数y=图像交x于A(,4).B(3,m)两点
(1)求m,n的值
(2)求直线 AB 的解析式;
(3)根据图像直接写出不等式kx+b>中x的取值范围.
22.如图,有长为12m的篱笆,现一面利用墙(墙的最大可用长度a为5m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
(1)要围成面积为9m2的花圃,AB的长是多少米?
(2)当AB的长是多少米时,围成的花圃面积最大?
六、解答题(四)(本大题2小题,每小题12分,共24分)
23.在矩形ABCD中,AB=3,BC=2,以点A为旋转中心,按逆时针方向旋转矩形ABCD,旋转角为α(0°<α <180°),得到矩形AEFG,点B、点C、点D的对应点分別为点E、点F、点G.
(1)如图1,当点E落在DC边上时,线段EC的长度为__________。
(2)如图②,连接CF,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
①求证:△ACD≌△CAE.
②求线段 DH 的长度.
(3)如图3,设点P为边GF的中点,连结PB、PE、BE,在矩形ABCD旋转的过程中,△BEP 面积的最大值为_____
24.抛物线y=ax2+bx-4(a≠0)与x轴交于点A(-2,0)和B(4,0),与y轴交于点C,连接BC.点P是线段BC下方抛物线上的一个动点(不与点 B,C重合),过点P作y轴的平行线交BC于M,交x轴于 N,设点 P 的横坐标为t.
(1)求该抛物线的解析式:
(2)用关于t的代数式表示线段PM,求PM的最大值及此时点M的坐标:
(3)过点C作CH⊥PN于点H,S△BMN=9S△CHM,
①求点P的坐标:
②连接CP,在 y轴上是否存在点 Q,使得△CPQ为直角三角形,若存在,求出点 Q的坐标:若不存在,请说明理由.
一、单选题(本大题10小题,每小题3分,共30分)
1 2 3 4 5 6 7 8 9 10
B B A В. D D A B C C
二、填空题(本大题5小题,每小题3分,共15分)
11. (1,-3)
12. - 5
13. 9
14. 4
15. 3 -3
三、解答题(一)(本大题2小题,每小题5分,共10分)
16.解:原方程化为:
(x﹣5 ) (x +3) =0.
∴ x1=5,x2=﹣3
17.证明:∵Δ=(﹣m)2– 4(m–1)=(m–2)2 ≥0,
∴方程总有两个实数根.
四、解答题(二)(本大题2小题,每小题7分,共14分)
18.(1)画出△A1OB1,如图.
点A1(0,1),点B1(-2,2).
(2)∵ OB1 = OB =
∴扇形BOB1面积=
∴线段OB扫过的面积2π.
19. 证明:如图,连接OA
∵ OA=OB,AD=ED,
∴∠OBE= ∠OAE,∠AED= ∠EAD.
∵∠OEB= ∠AED,
∴∠OEB= ∠EAD,
∵OD⊥OB,
∴∠BOΕ = 90°,
∴∠OBE+∠OEB= 90°,
∴∠OAE+ ∠EAD= 90°,
∴∠OAD=90°,
又∵OA是⊙O的半径,
∴AD是⊙O的切线.
五、解答题(三)(本大题3小题,每小题9分,共27分)
20.(1)解:接受问卷调查的学生共有,29÷58%=50(人);
条形统计图中m的值为:50-4-29-10=7(人);
故答案为:50;7.
(2)解:达到“不了解”和“了解很少”程度的总人数为:
(10+7)÷50×1500=510(人);
故答案为:510.
(3)解:由题意列树状图:
由树状图可知,所有等可能的结果有12种,恰好抽到1名男生和1名女生的结果有8种,
∴恰好抽到1名男生和1名女生的概率为:
21.解:(1)∵一次函数y=kx+b的图像与反比例函数y=图像交x于(,4).B(3,m)
∴ n=×4= 6 .
y=
将B(3,m)代入y= y=
得m==2.
∴B(3,2);
(2)将A(,4),B(3,2)代入y=kx+b得:
解的:
∴直线AB的解析式为y=-x+6;
(3)∵A(,4),B(3,2)
结合函数图象可知:当x<0或
即不等式kx+b>的解集为:x<0或
∴S=x(12-3x)=-3x2+12x.
当S=9时,
-3x2+12x=9
解得x1= 1,x2 =3,
当x =1时,12-3x =12-3=9>5,不符合题意,舍去,
当x =3时,12-3x =12-9=3<5,符合题意,
∴要围成面积为9m2的花圃,AB的长是3米;
(2)由题意,可知:
∴< x≤4,
∵S=-3x2+12x =-3(x -2)2+12.
∵-3<0,抛物线开口向下,且对称轴为直线x=2
∴在
六、解答题(四)(本大题2小题,每小题12分,共24分)
23.解:(1)如图①中
∵ 四边形ABCD是矩形,
∴AB = CD = 3,BC = AD = 2,∠D = 90°,
∵矩形AEFG是由矩形ABCD旋转得到,
∴AE = AB = 3,
在RtΔADE中,DE = ,
∴CE =,
故答案为:.
(2)①证明:如图②中,
∵当点E落在线段CF上,
∴∠AEC = ∠ADC = 90,
在Rt△ADC和Rt△AEC中,
∴RtΔACD≌RtΔCAE(HL)
②如图②中,△ACD≌△CAE,
∴∠ACD =∠EAC
∴ AH = HC
设AH = HC =m
在RtΔADH中,:AD2 + DH2= AH2,
∴22 +(3-m)2 = m2
m=
∴DH =
故答案为:
(3)解:如图3中,连接PA,作AM ⊥PE于M.
当AM与AB共线,且BM=BA+AM时,△BPE面积最大
由题意:PF=PG=.
∵AG= EF =2,∠G= ∠F= 90°
∴PA=PE=.
∵S△APE=S矩形AGFE=PE·AM.
∴AM= = =
则S△BPE=PE·BM=××(3+)=
△PBE的面积的最大值为
故答案为:
24.解(1)∵抛物线y=ax2+bx-4(a≠0)与x轴交于点A(-2,0)和B(4,0)
∴
解得:
∴该抛物线的解析式为:y=x2-x-4
(2)在y=x2-x-4中,令x=0,得y=-4,
∴ C(0,-4),
设直线BC的解析式为y=kx+c,
∴
解得:
∴直线BC的解析式为y=x-4,
设P(t,t 2-t-4),则M(t, t-4),
∴PM= t-4-(t 2-t-4)=-(t-2)2+2
∵-<0.
∴当t =2时,PM取得最大值2,
此时点M的坐标为(2,-2);
(3)解:①如图1,
∵(t,t 2-t-4),M(t, t-4),N(t,0),B(4,0),C(0,-4),CH⊥PN.
∴BN=4-t,MN=4-t,CH = t,MH= t -4-(-4)= t
∵S△BMN=9S△CHM
∴(4-t)2=9×t 2
解得:t 1=1,t 2=-2,
∵点P是线段BC下方抛物线上的一个动点
∴0
∴P(1,-)
②存在点Q使得△CPQ为直角三角形,设Q(0,m)
∵C(0,-4).P(1,-).
CP2=(1-0)2+(-+4)2=.
CQ2=(-4-m)2
PQ2= t 2+(--m)2,∠PCQ≠90°
当∠CQP=90°时,如图2,PQ⊥y轴
∴Q(0. -)
当∠CPQ=90°时,如图3,
在RtΔCPQ中,CP2+PQ2=CQ2
+ t 2+(--m)2 =(-4-m)2
解得:m=-
∴Q(0. -)
综上所述,点Q的坐标为(0、-)或(0. -).
同课章节目录
