北师版数学必修1函数模型的应用实例
图片预览






文档简介
课件16张PPT。3.2.2函数模型的应用实例目标:
(1)感受各种函数的广泛应用;
(2)体会解决实际问题时建立函数模型的过程 一辆汽车在某段路程中的行驶速率与时间关系如图所示:
(1)求图中阴影部分的面积,并说明所求面积的实际含义。
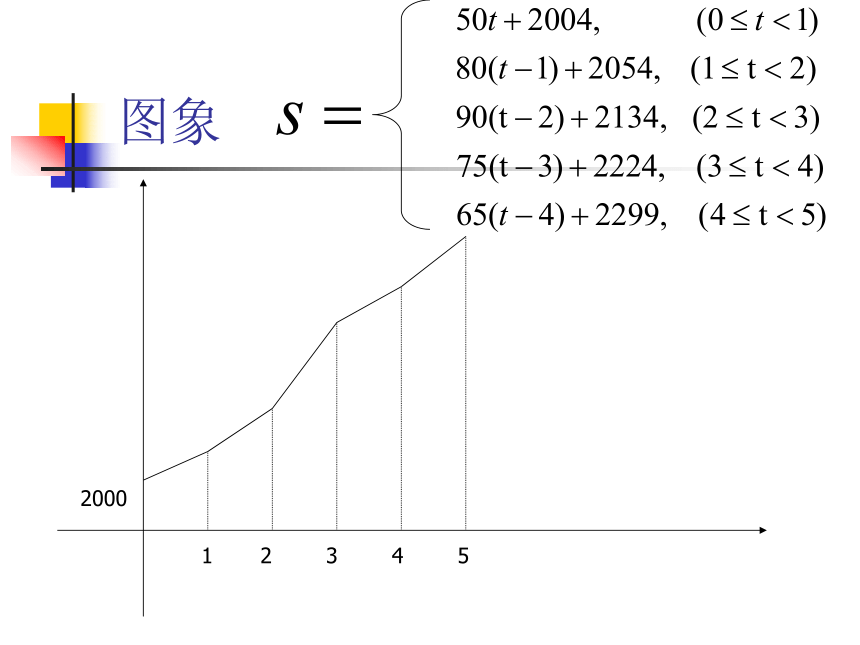
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004千米,试建立行驶这段路程时汽车里程表读数s千米与时间t小时的函数解析式。并作出该函数的图象。图象例4人口问题是当今世界各国普遍关注的问题。英国经济学家T.R.Malthus就提出了自然状态下的人口增长模型:
其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年平均增长率。
下表是1950-1959年我国人口数据资料年份:1950 1951 1952 1953 1954 1955 1956 1957 1958 1959
人数 55196 56300 57482 58796 60266 61456 62828 64563 65994 67207
(万) (1)如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.001),用Malthus人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;
(2)按上表增长趋势,大约哪年我国人口达到13亿?分析每年增长率不同:1951—1959年各年的增长率设为:求平均增长率:描点,画图,看是否基本符合?注意:用已知函数模型刻画实际问题时,由于实际问题的条件与得到已知模型的条件会有所不同,因此需要对模型进行修正。第2节上节目标:能够用已知的函数模型解决问题。
本节目标:还要能够在面临实际问题时,通过自己建立函数模型来解决问题。例5某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元。销售单价与日均销售量的关系如表所示: 根据数据进行分析,怎样定价才能获得最大利润?解:根据表格销售单价每增加1元,日均销售量就减少40桶。设在进价的基础上增加x元,日均销售利润为y元;
销售量:480-40(x-1)=520-40x(桶)
利润:y=(520-40x)x-200
=-40x2+520x-200
(0体重 6.13 7.90 9.99 12.15 15.02 17.50 20.92 26.86 31.11 38.85 47.25 55.05
根据表格提供的数据,能否建立恰当的函数模型,使它能比较近似地反映这个地区未成年男性体重y(kg)与身高x(cm)的函数关系?写出函数模型的解析式。
若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175cm,体重为78kg的在校男生体重是否正常?分析:描点、画图。解:以身高为横坐标,以体重为纵坐标,画出散点图,根据点的分布,考虑y=a×bx作模型。(1)取其中两组数据(70,7.79),(160,47.25)代入y=a×bx 得:经验证,该模型符合实际。(2)将x=175代入模型得:y=63.98
78÷63.98≈1.22>1.2
所以偏胖。
假如不符合实际怎么办?总结 建立模型解决问题的步骤收集数据画散点图选择函数模型求函数模型检验用函数模型解释实际问题
(1)感受各种函数的广泛应用;
(2)体会解决实际问题时建立函数模型的过程 一辆汽车在某段路程中的行驶速率与时间关系如图所示:
(1)求图中阴影部分的面积,并说明所求面积的实际含义。
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004千米,试建立行驶这段路程时汽车里程表读数s千米与时间t小时的函数解析式。并作出该函数的图象。图象例4人口问题是当今世界各国普遍关注的问题。英国经济学家T.R.Malthus就提出了自然状态下的人口增长模型:
其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年平均增长率。
下表是1950-1959年我国人口数据资料年份:1950 1951 1952 1953 1954 1955 1956 1957 1958 1959
人数 55196 56300 57482 58796 60266 61456 62828 64563 65994 67207
(万) (1)如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.001),用Malthus人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;
(2)按上表增长趋势,大约哪年我国人口达到13亿?分析每年增长率不同:1951—1959年各年的增长率设为:求平均增长率:描点,画图,看是否基本符合?注意:用已知函数模型刻画实际问题时,由于实际问题的条件与得到已知模型的条件会有所不同,因此需要对模型进行修正。第2节上节目标:能够用已知的函数模型解决问题。
本节目标:还要能够在面临实际问题时,通过自己建立函数模型来解决问题。例5某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元。销售单价与日均销售量的关系如表所示: 根据数据进行分析,怎样定价才能获得最大利润?解:根据表格销售单价每增加1元,日均销售量就减少40桶。设在进价的基础上增加x元,日均销售利润为y元;
销售量:480-40(x-1)=520-40x(桶)
利润:y=(520-40x)x-200
=-40x2+520x-200
(0
根据表格提供的数据,能否建立恰当的函数模型,使它能比较近似地反映这个地区未成年男性体重y(kg)与身高x(cm)的函数关系?写出函数模型的解析式。
若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175cm,体重为78kg的在校男生体重是否正常?分析:描点、画图。解:以身高为横坐标,以体重为纵坐标,画出散点图,根据点的分布,考虑y=a×bx作模型。(1)取其中两组数据(70,7.79),(160,47.25)代入y=a×bx 得:经验证,该模型符合实际。(2)将x=175代入模型得:y=63.98
78÷63.98≈1.22>1.2
所以偏胖。
假如不符合实际怎么办?总结 建立模型解决问题的步骤收集数据画散点图选择函数模型求函数模型检验用函数模型解释实际问题
