人教版七年级数学下册第六章 实数 单元检测卷(含解析)
文档属性
| 名称 | 人教版七年级数学下册第六章 实数 单元检测卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 213.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 11:11:21 | ||
图片预览



文档简介
第六章 实数 单元检测卷 人教版七年级数学下册
一、选择题
1.64的平方根是( )
A. 4 B.±4 C.8 D.±8
2.的平方根是 ( )
A.4 B.2 C.±4 D.±2
3.下列运算正确的是( )
A. B. C. D.
4.式子中,x的取值范围是( )
A. B. C. D.
5.下列各式中正确的是( )
A. B. C. D.
6.面积为 2 的正方形的边长是( )
A.2的平方根 B.2的算术平方根
C.2开平方的结果 D.2的立方根
7. 下列说法错误的是( )
A.的立方根是
B.算术平方根等于本身的数是,
C.
D.的平方根是
8.下列各数中的无理数是( )
A. B. C.0 D.
9.比较2, , 的大小,正确的是( )
A.2< < B.2< < C. <2< D. < <2
10.按如图所示的程序计算,若开始输入的x的值是64,则输出的y的值是( )
A. B. C.2 D.3
二、填空题
11.一个自然数的算术平方根是a,则相邻的下一个自然数的算术平方根是 .
12.在等式中,( )内的数等于 .
13.依据图中呈现的运算关系,可知 .
14.已知 为两个连续的整数,且 ,则 = .
三、计算题
15.计算:
16.解方程:
(1);
(2)
四、解答题
17.已知实数的一个平方根是-5,的立方根是-2,求的算术平方根.
18.有一块矩形木板,木工采用如图的方式,在木板上截出两个面积分别为18dm2和32dm2的正方形木板.
(1)截出的两块正方形木料的边长分别为 .
(2)求剩余木料的面积.
(3)如果木工想从剩余的木料中截出长为1.5dm,宽为1dm的长方形木条,最多能截出多少块这样的木条.
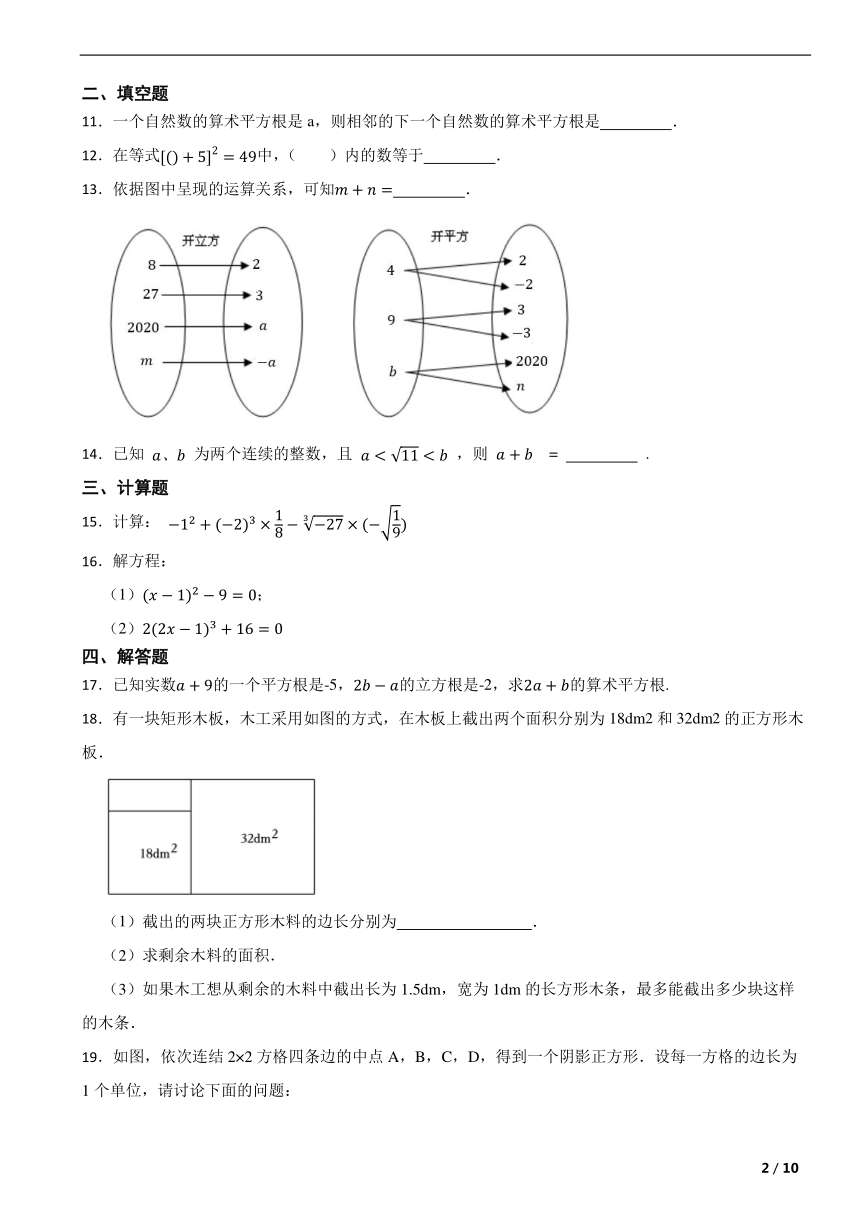
19.如图,依次连结2×2方格四条边的中点A,B,C,D,得到一个阴影正方形.设每一方格的边长为1个单位,请讨论下面的问题:
(1)阴影正方形的面积是多少?
(2)阴影正方形的边长是多少?应怎样表示?
(3)阴影正方形的边长介于哪两个相邻整数之间?
20.已知的立方根是2,的算术平方根是4,c是的整数部分.
(1)求a、b、c的值;
(2)求的平方根.
21.如果要制作一个立方体,使它的体积是已知立方体体积的27倍,那么它的棱长应是已知立方体的棱长的几倍?
22.比较和的大小.
23.把下列各有理数:﹣(+4),|﹣3|,0,﹣5,1.5
(1)分别在数轴上表示出来:
(2)将上述有理数填入图中相应的圈内.
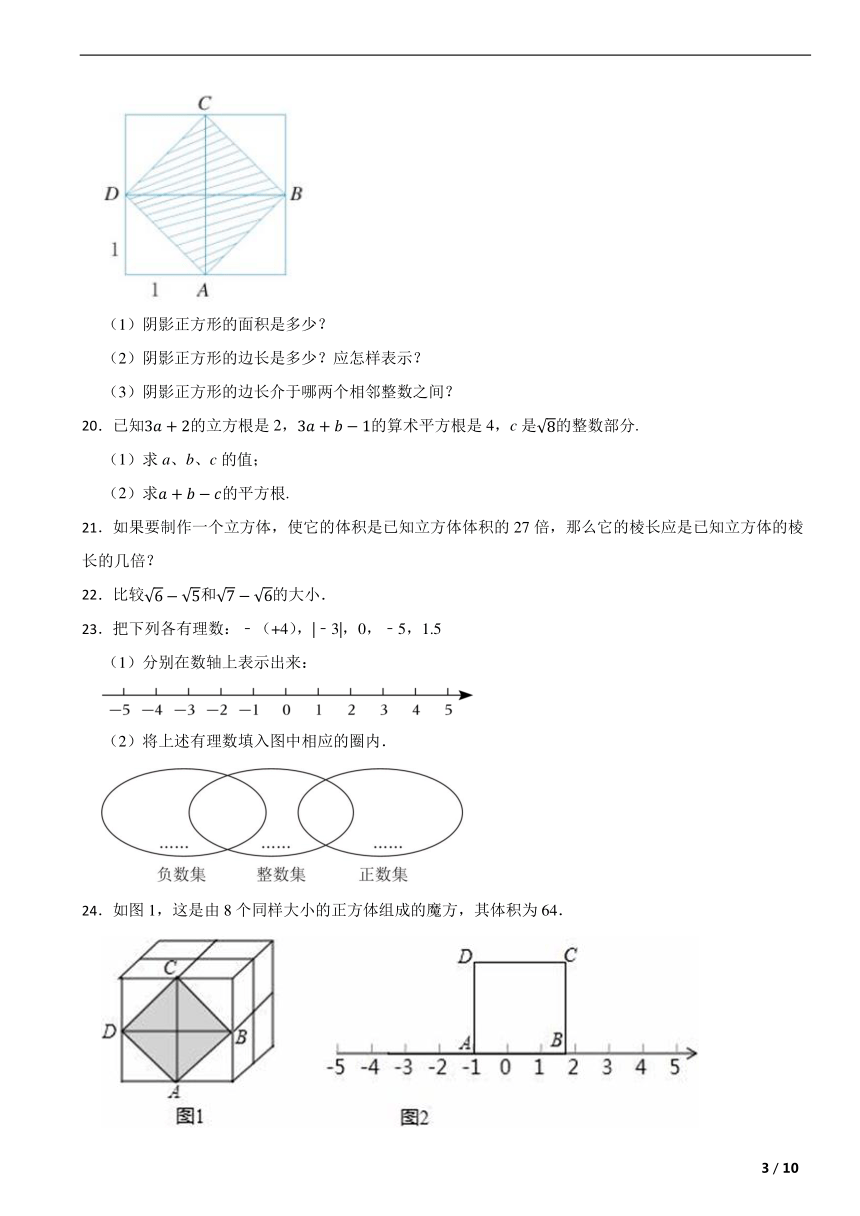
24.如图1,这是由8个同样大小的正方体组成的魔方,其体积为64.
(1)求出这个魔方的棱长;
(2)图1中阴影部分是一个正方形ABCD,求出阴影部分的边长及其面积;
(3)如图2,把正方形ABCD放到数轴上,使点A与﹣1重合,那么点B表示的数为a,请计算(a﹣1)(a+1)﹣|2﹣a|的值.
答案解析部分
1.【答案】D
【解析】【解答】解:∵(±8)2=64,
∴64的平方根是±8,
故答案为:D.
【分析】直接根据平方根的定义即可求解.
2.【答案】D
【解析】【分析】首先根据平方根的定义求出4的平方根,然后就可以解决问题.
【解答】∵=4
∵±2的平方等于4,
∴4的平方根是:±2.
故选D.
【点评】此题主要考查了平方根的定义和性质,根据平方根的定义得出是解决问题的关键.
3.【答案】C
【解析】【解答】根据算术平方根,平方,绝对值的定义,得:A. B. C. D. .
故答案为:C.
【分析】根据算术平方根,绝对值的定义及有理数的乘方分别求出结果,然后判断即可.
4.【答案】A
【解析】【解答】解: 根据题意得:x-2≥0,
解得x≥2.
故答案为:A.
【分析】 根据算数平方根有意义的条件,被开方数是非负数即可求解.
5.【答案】C
【解析】【解答】解:A、,故选项A错误;
B、负数没有平方根,故选项B错误;
C、,故选项C正确;
D、,故选项D错误.
故答案为:C.
【分析】正数的正平方根叫做算术平方根,据此可判断A选项;负数没有平方根,据此可判断B选项;如果一个数的立方等于a,那么这个数叫做a的立方根,据此可判断C选项;求一个带分数的算术平方根,需要将这个带分数化为假分数,进而将分子分母分别开方,据此可判断D选项.
6.【答案】B
【解析】【解答】解:面积为2的正方形的边长是2的算术平方根.
故答案为:B .
【分析】由于正方形的面积等于边长的平方,且正方形的边长是一个正数,故可以根据算术平方根的定义求解.
7.【答案】B
【解析】【解答】A、∵的立方根是,∴A正确,不符合题意;
B、∵-1没有算术平方根,∴B不正确,符合题意;
C、∵,∴C正确,不符合题意;
D、∵的平方根是,∴D正确,不符合题意;
故答案为:B.
【分析】利用立方根、平方根的性质及计算方法逐项判断即可.
8.【答案】B
【解析】【解答】解:A.=2是有理数,故不符合题意;
B.是无理数,故符合题意;
C.0是有理数,故不符合题意;
D.是有理数,故不符合题意;
故答案为:B.
【分析】根据无理数的定义逐项判断即可。
9.【答案】C
【解析】【解答】解:∵1<<2,2<<3
∴<2<
故答案为:C
【分析】根据题意判断和分别在哪两个整数之间,即可判断它们的大小。
10.【答案】A
【解析】【解答】解:∵当x=64时, , ,2是有理数,
∴当x=2时,算术平方根为 是无理数,
∴y= ,
故答案为:A.
【分析】当x=64时,求算术平方根,再判断其算术平方根是否为无理数,然后不断求算术平方根,直到其算术平方根是无理数为止.
11.【答案】
【解析】【解答】∵一个自然数的算术平方根是a,
∴这个自然数是a2,
∴相邻的下一个自然数为:a2+1,
∴相邻的下一个自然数的算术平方根是: ,
故答案为: .
【分析】首先利用算术平方根求出这个自然数,然后即可求出相邻的下一个自然数的算术平方根.
12.【答案】2或-12
【解析】【解答】解:∵,
∴,
∴=2或-12,
故答案为:2或-12.
【分析】根据平方根的意义可得,据此分别求解即可.
13.【答案】
【解析】【解答】解:∵a与-a互为相反数,
∴m=-2020,
∵2020和n是b的平方根,
∴n=-2020,
∴m+n=-2020+(-2020)=-4040.
故答案为:-4040.
【分析】根据互为相反数的两个数的两根互为相反数可得m的值,根据一个正数有两个平方根,且这两个平方根互为相反数求出n的值,即可得出m+n的值.
14.【答案】7
【解析】【解答】解:∵ < < ,
∴3< <4;
故a=3,b=4;
所以a+b=7.
故答案为7.
15.【答案】解:原式=﹣1﹣8× +3×(﹣ )
=﹣1﹣1﹣1
=﹣3.
【解析】【分析】根据有理数的乘方、立方根、算术平方根的性质进行计算即可
16.【答案】解:,, , 或; .
【答案】解:,,,,.
(1)解:,
,
,
或 .
(2)解:,
,
,
,
.
【解析】【分析】(1)根据平方根的定义解方程,即可求解;
(2)根据立方根的定义解方程,即可求解.
17.【答案】解:由题意得, , .
∴ , .
∴ .
∴ 的算术平方根是6.
【解析】【分析】利用算术平方根和立方根的性质,可得到关于a,b的方程组,解方程组求出a,b的值,再代入求出2a+b的值,然后求出2a+b的算术平方根.
18.【答案】(1),
(2)解:根据题意得:矩形的长为,宽为,
∴剩余木料的面积;
(3)解:根据题意得:从剩余的木料的长为,宽为,
∵,,
∴能截出2×1=2块这样的木条.
【解析】【解答】(1)小正方形的边长为dm;大正方形的边长为dm,
故答案为:;.
【分析】(1)利用正方形的面积及平方根的计算方法求出正方形的边长即可;
(2)先求出矩形的长和宽,再利用矩形的面积公式求解即可;
(3)先求出剩余木料的长和宽,再求解即可.
19.【答案】(1)解:由题意得: 阴影正方形的面积==2.
(2)解:阴影正方形的边长=.
(3)解:∵1<<2
∴ 阴影正方形的边长介于 1和2之间.
【解析】【分析】(1)阴影正方形的面积=对角线乘积的一半;
(2)边长=面积的算术平方根,即可求得;
(3)估算的大小即可。.
20.【答案】(1)解:∵的立方根是2,的算术平方根是4,
∴,,
解得:,,
∵,
∴,
∴的整数部分是2,
∴,
∴,,;
(2)解:∵,,,
∴,
∴的平方根是.
【解析】【分析】(1)先利用立方根、算术平方根和估算无理数大小的方法求出a、b、c的值即可;
(2)将a、b、c的值代入计算即可.
21.【答案】解:由题意得:制作的立方体的体积:已知立方体的体积=27:1,
所以,制作的立方体的棱长:已知立方体的棱长=3:1,
即它的棱长是已知立方体的棱长的3倍.
【解析】【分析】根据体积=棱长3,即可根据体积比算出棱长比.
22.【答案】, .
∵>0
∴>0
∴
【解析】【分析】利用作差法比较数值大小,,对式子平方,结合完全平方公式即可得解.
23.【答案】(1)解:﹣(+4)=﹣4,|﹣3|=3,
把各数表示在数轴上如下,
(2)解:如图,
【解析】【分析】(1)先根据有理数的运算化简,进而即可表示在数轴上;
(2)根据实数的分类结合题意即可求解。
24.【答案】(1)解:这个魔方的棱长为:=4
(2)解:每个小正方体的棱长为:4÷2=2;
阴影部分的边长为:CD==2,
阴影部分的面积为:CD2=(2)2=8
(3)解:根据图可知a=2﹣1,
(a﹣1)(a+1)﹣|2﹣a|
=(2﹣1﹣1)×(2﹣1+1)﹣|2﹣(2﹣1)|
=(2﹣2)×2﹣|3﹣2|
=8﹣4﹣3+2
=5﹣2.
【解析】【分析】(1)正方体体积已知,正方体体积公式为V正方体=棱长3,所以棱长为4;
(2)第一问已知大正方体边长,继而可求小正方体边长,则阴影部分正方形的边长和面积也能求出来。
(3)根据第二问AB边长,可得B的值,然后带入原式进行化简即可。
1 / 1
一、选择题
1.64的平方根是( )
A. 4 B.±4 C.8 D.±8
2.的平方根是 ( )
A.4 B.2 C.±4 D.±2
3.下列运算正确的是( )
A. B. C. D.
4.式子中,x的取值范围是( )
A. B. C. D.
5.下列各式中正确的是( )
A. B. C. D.
6.面积为 2 的正方形的边长是( )
A.2的平方根 B.2的算术平方根
C.2开平方的结果 D.2的立方根
7. 下列说法错误的是( )
A.的立方根是
B.算术平方根等于本身的数是,
C.
D.的平方根是
8.下列各数中的无理数是( )
A. B. C.0 D.
9.比较2, , 的大小,正确的是( )
A.2< < B.2< < C. <2< D. < <2
10.按如图所示的程序计算,若开始输入的x的值是64,则输出的y的值是( )
A. B. C.2 D.3
二、填空题
11.一个自然数的算术平方根是a,则相邻的下一个自然数的算术平方根是 .
12.在等式中,( )内的数等于 .
13.依据图中呈现的运算关系,可知 .
14.已知 为两个连续的整数,且 ,则 = .
三、计算题
15.计算:
16.解方程:
(1);
(2)
四、解答题
17.已知实数的一个平方根是-5,的立方根是-2,求的算术平方根.
18.有一块矩形木板,木工采用如图的方式,在木板上截出两个面积分别为18dm2和32dm2的正方形木板.
(1)截出的两块正方形木料的边长分别为 .
(2)求剩余木料的面积.
(3)如果木工想从剩余的木料中截出长为1.5dm,宽为1dm的长方形木条,最多能截出多少块这样的木条.
19.如图,依次连结2×2方格四条边的中点A,B,C,D,得到一个阴影正方形.设每一方格的边长为1个单位,请讨论下面的问题:
(1)阴影正方形的面积是多少?
(2)阴影正方形的边长是多少?应怎样表示?
(3)阴影正方形的边长介于哪两个相邻整数之间?
20.已知的立方根是2,的算术平方根是4,c是的整数部分.
(1)求a、b、c的值;
(2)求的平方根.
21.如果要制作一个立方体,使它的体积是已知立方体体积的27倍,那么它的棱长应是已知立方体的棱长的几倍?
22.比较和的大小.
23.把下列各有理数:﹣(+4),|﹣3|,0,﹣5,1.5
(1)分别在数轴上表示出来:
(2)将上述有理数填入图中相应的圈内.
24.如图1,这是由8个同样大小的正方体组成的魔方,其体积为64.
(1)求出这个魔方的棱长;
(2)图1中阴影部分是一个正方形ABCD,求出阴影部分的边长及其面积;
(3)如图2,把正方形ABCD放到数轴上,使点A与﹣1重合,那么点B表示的数为a,请计算(a﹣1)(a+1)﹣|2﹣a|的值.
答案解析部分
1.【答案】D
【解析】【解答】解:∵(±8)2=64,
∴64的平方根是±8,
故答案为:D.
【分析】直接根据平方根的定义即可求解.
2.【答案】D
【解析】【分析】首先根据平方根的定义求出4的平方根,然后就可以解决问题.
【解答】∵=4
∵±2的平方等于4,
∴4的平方根是:±2.
故选D.
【点评】此题主要考查了平方根的定义和性质,根据平方根的定义得出是解决问题的关键.
3.【答案】C
【解析】【解答】根据算术平方根,平方,绝对值的定义,得:A. B. C. D. .
故答案为:C.
【分析】根据算术平方根,绝对值的定义及有理数的乘方分别求出结果,然后判断即可.
4.【答案】A
【解析】【解答】解: 根据题意得:x-2≥0,
解得x≥2.
故答案为:A.
【分析】 根据算数平方根有意义的条件,被开方数是非负数即可求解.
5.【答案】C
【解析】【解答】解:A、,故选项A错误;
B、负数没有平方根,故选项B错误;
C、,故选项C正确;
D、,故选项D错误.
故答案为:C.
【分析】正数的正平方根叫做算术平方根,据此可判断A选项;负数没有平方根,据此可判断B选项;如果一个数的立方等于a,那么这个数叫做a的立方根,据此可判断C选项;求一个带分数的算术平方根,需要将这个带分数化为假分数,进而将分子分母分别开方,据此可判断D选项.
6.【答案】B
【解析】【解答】解:面积为2的正方形的边长是2的算术平方根.
故答案为:B .
【分析】由于正方形的面积等于边长的平方,且正方形的边长是一个正数,故可以根据算术平方根的定义求解.
7.【答案】B
【解析】【解答】A、∵的立方根是,∴A正确,不符合题意;
B、∵-1没有算术平方根,∴B不正确,符合题意;
C、∵,∴C正确,不符合题意;
D、∵的平方根是,∴D正确,不符合题意;
故答案为:B.
【分析】利用立方根、平方根的性质及计算方法逐项判断即可.
8.【答案】B
【解析】【解答】解:A.=2是有理数,故不符合题意;
B.是无理数,故符合题意;
C.0是有理数,故不符合题意;
D.是有理数,故不符合题意;
故答案为:B.
【分析】根据无理数的定义逐项判断即可。
9.【答案】C
【解析】【解答】解:∵1<<2,2<<3
∴<2<
故答案为:C
【分析】根据题意判断和分别在哪两个整数之间,即可判断它们的大小。
10.【答案】A
【解析】【解答】解:∵当x=64时, , ,2是有理数,
∴当x=2时,算术平方根为 是无理数,
∴y= ,
故答案为:A.
【分析】当x=64时,求算术平方根,再判断其算术平方根是否为无理数,然后不断求算术平方根,直到其算术平方根是无理数为止.
11.【答案】
【解析】【解答】∵一个自然数的算术平方根是a,
∴这个自然数是a2,
∴相邻的下一个自然数为:a2+1,
∴相邻的下一个自然数的算术平方根是: ,
故答案为: .
【分析】首先利用算术平方根求出这个自然数,然后即可求出相邻的下一个自然数的算术平方根.
12.【答案】2或-12
【解析】【解答】解:∵,
∴,
∴=2或-12,
故答案为:2或-12.
【分析】根据平方根的意义可得,据此分别求解即可.
13.【答案】
【解析】【解答】解:∵a与-a互为相反数,
∴m=-2020,
∵2020和n是b的平方根,
∴n=-2020,
∴m+n=-2020+(-2020)=-4040.
故答案为:-4040.
【分析】根据互为相反数的两个数的两根互为相反数可得m的值,根据一个正数有两个平方根,且这两个平方根互为相反数求出n的值,即可得出m+n的值.
14.【答案】7
【解析】【解答】解:∵ < < ,
∴3< <4;
故a=3,b=4;
所以a+b=7.
故答案为7.
15.【答案】解:原式=﹣1﹣8× +3×(﹣ )
=﹣1﹣1﹣1
=﹣3.
【解析】【分析】根据有理数的乘方、立方根、算术平方根的性质进行计算即可
16.【答案】解:,, , 或; .
【答案】解:,,,,.
(1)解:,
,
,
或 .
(2)解:,
,
,
,
.
【解析】【分析】(1)根据平方根的定义解方程,即可求解;
(2)根据立方根的定义解方程,即可求解.
17.【答案】解:由题意得, , .
∴ , .
∴ .
∴ 的算术平方根是6.
【解析】【分析】利用算术平方根和立方根的性质,可得到关于a,b的方程组,解方程组求出a,b的值,再代入求出2a+b的值,然后求出2a+b的算术平方根.
18.【答案】(1),
(2)解:根据题意得:矩形的长为,宽为,
∴剩余木料的面积;
(3)解:根据题意得:从剩余的木料的长为,宽为,
∵,,
∴能截出2×1=2块这样的木条.
【解析】【解答】(1)小正方形的边长为dm;大正方形的边长为dm,
故答案为:;.
【分析】(1)利用正方形的面积及平方根的计算方法求出正方形的边长即可;
(2)先求出矩形的长和宽,再利用矩形的面积公式求解即可;
(3)先求出剩余木料的长和宽,再求解即可.
19.【答案】(1)解:由题意得: 阴影正方形的面积==2.
(2)解:阴影正方形的边长=.
(3)解:∵1<<2
∴ 阴影正方形的边长介于 1和2之间.
【解析】【分析】(1)阴影正方形的面积=对角线乘积的一半;
(2)边长=面积的算术平方根,即可求得;
(3)估算的大小即可。.
20.【答案】(1)解:∵的立方根是2,的算术平方根是4,
∴,,
解得:,,
∵,
∴,
∴的整数部分是2,
∴,
∴,,;
(2)解:∵,,,
∴,
∴的平方根是.
【解析】【分析】(1)先利用立方根、算术平方根和估算无理数大小的方法求出a、b、c的值即可;
(2)将a、b、c的值代入计算即可.
21.【答案】解:由题意得:制作的立方体的体积:已知立方体的体积=27:1,
所以,制作的立方体的棱长:已知立方体的棱长=3:1,
即它的棱长是已知立方体的棱长的3倍.
【解析】【分析】根据体积=棱长3,即可根据体积比算出棱长比.
22.【答案】, .
∵>0
∴>0
∴
【解析】【分析】利用作差法比较数值大小,,对式子平方,结合完全平方公式即可得解.
23.【答案】(1)解:﹣(+4)=﹣4,|﹣3|=3,
把各数表示在数轴上如下,
(2)解:如图,
【解析】【分析】(1)先根据有理数的运算化简,进而即可表示在数轴上;
(2)根据实数的分类结合题意即可求解。
24.【答案】(1)解:这个魔方的棱长为:=4
(2)解:每个小正方体的棱长为:4÷2=2;
阴影部分的边长为:CD==2,
阴影部分的面积为:CD2=(2)2=8
(3)解:根据图可知a=2﹣1,
(a﹣1)(a+1)﹣|2﹣a|
=(2﹣1﹣1)×(2﹣1+1)﹣|2﹣(2﹣1)|
=(2﹣2)×2﹣|3﹣2|
=8﹣4﹣3+2
=5﹣2.
【解析】【分析】(1)正方体体积已知,正方体体积公式为V正方体=棱长3,所以棱长为4;
(2)第一问已知大正方体边长,继而可求小正方体边长,则阴影部分正方形的边长和面积也能求出来。
(3)根据第二问AB边长,可得B的值,然后带入原式进行化简即可。
1 / 1
