最新人教版七下数学 6.1 平方根 第3课时 课件(共35张PPT)
文档属性
| 名称 | 最新人教版七下数学 6.1 平方根 第3课时 课件(共35张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 00:00:00 | ||
图片预览








文档简介
(共35张PPT)
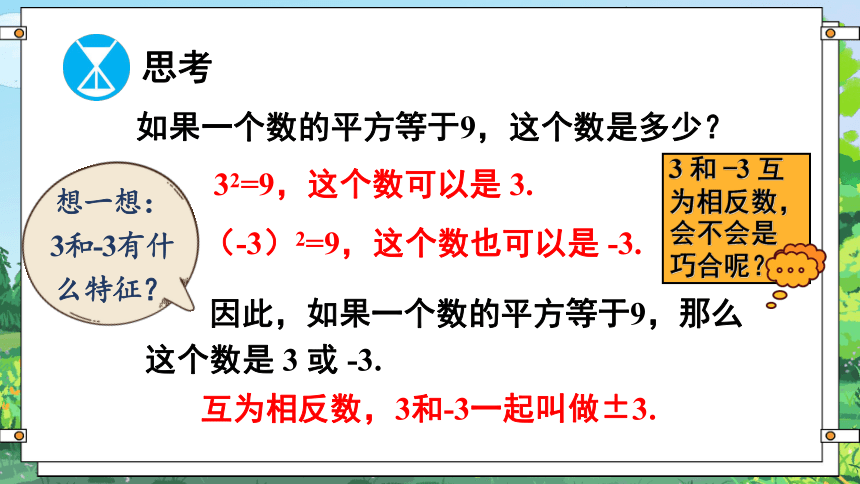
本章概览
乘方
开方
平方根
立方根
实数
实数的概念及性质
实数的大小比较与运算
互为
逆运算
开平方
开立方
平方根
算术 平方根
算术平方根的估算
平方根
平方根
人教版七年级下册
第3课时 平方根
第六章 实数
6.1 平方根
1. 一般地,如果一个_______的平方等于 a,即 x2=a,那么这个_______叫做 a 的算术平方根.
2. 填空:(1)22=_____,(-2)2=_____;
(2)0.82=_____,(-0.8)2=_____.
3. 想一想:5的平方等于25,5叫做25的算术平方根. -5的平方也等于25,那么-5叫做25的什么根呢?
正数x
4
4
0.64
正数x
0.64
复习回顾
思考
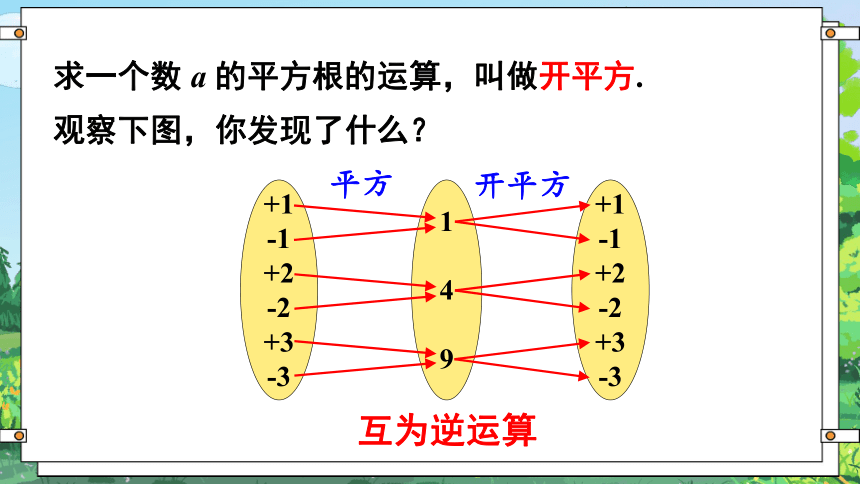
如果一个数的平方等于9,这个数是多少?
32=9,这个数可以是 3.
(-3)2=9,这个数也可以是 -3.
因此,如果一个数的平方等于9,那么这个数是 3 或 -3.
想一想: 3和-3有什么特征?
3 和 -3 互 为相反数,会不会是 巧合呢?
互为相反数,3和-3一起叫做±3.
x2 1 16 0 49
x
填表:
±1
±4
0
±7
如果我们把上述填表的 x 的值分别叫做1,16,0,49, 的平方根,你能类比算术平方根的概念,给出平方根的概念吗?
探究新知
概念
引入
一般地,如果一个数的平方等于 a,那么这个数叫做 a 的平方根或二次方根. 这就是说,如果 x2=a,那么 x 叫做 a 的平方根.
平方根
二次方根
例如,3 和 -3 是 9 的平方根,
简记为±3是 9 的平方根.
你还能再举几个平方根的例子吗?
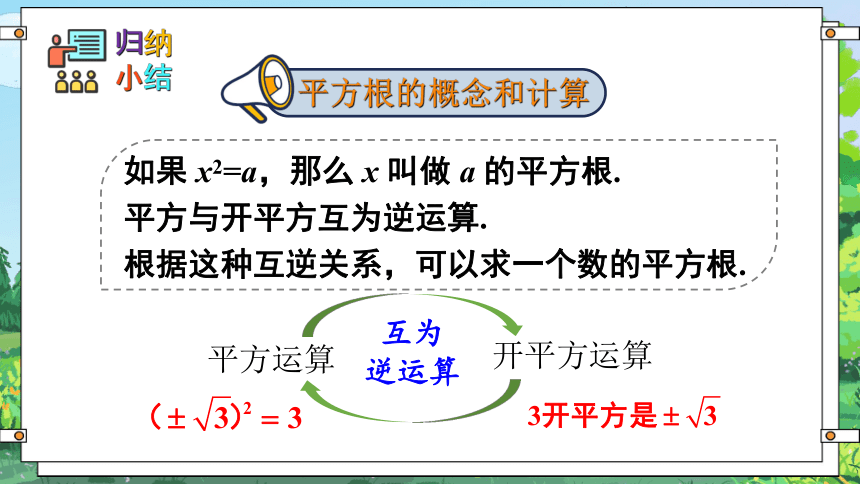
求一个数 a 的平方根的运算,叫做开平方.
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
观察下图,你发现了什么?
平方
开平方
互为逆运算
归纳
小结
平方根的概念和计算
如果 x2=a,那么 x 叫做 a 的平方根.
平方与开平方互为逆运算.
根据这种互逆关系,可以求一个数的平方根.
互为 逆运算
平方运算
开平方运算
例 4 求下列各数的平方根:
(1)100; (2) ; (3)0.25.
解:(1)因为(±10)2=100,所以100的平方根是±10;
(2)因为 ,所以 的平方根是± ;
(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
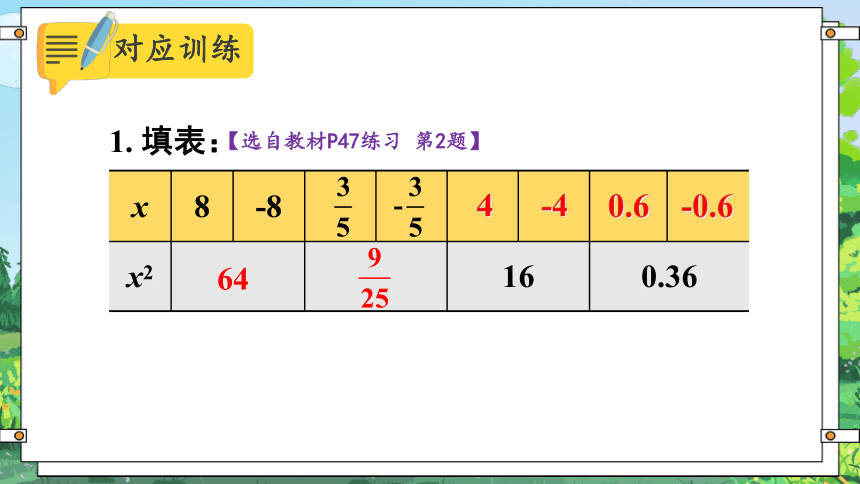
x 8 -8
x2 16 0.36 1. 填表:
64
4
-4
0.6
-0.6
【选自教材P47练习 第2题】
对应训练
2. 求下列各数的平方根:
(1)64;(2)0.09;(3) ;(4)(-7)2.
解:(1)因为(±8)2=64,所以64的平方根是±8;
(3)因为 ,所以 的平方根是± ;
(4)因为(±7)2=(-7)2=49,所以(-7)2的平方根
是±7.
(2)因为(±0.3)2=0.09,所以0.09的平方根是±0.3;
思考
1,4,9的平方根分别是多少?
正数的平方根有什么特点?
1,4,9的平方根分别是±1,±2,±3.
正数有两个平方根,它们互为相反数,其中正的平方根就是这个数的算术平方根.
0有几个平方根?各是多少?为什么?
0 只有一个平方根,是 0. 因为 02=0,并且任何一个不为 0 的数的平方都不等于 0,所以 0 的平方根是 0.
思考
-1,-4,-9有平方根吗?为什么?
没有. 正数的平方是正数,0 的平方是 0,负数的平方也是正数,即在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根.
归 纳
正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
1. 判断下列说法是否正确:
【选自教材P46练习 第1题】
(1)0的平方根是0;
(2)1的平方根是1;
(3)-1的平方根是-1;
(4)0.01是0.1的一个平方根.
1的平方根是±1.
-1没有平方根.
0.1是0.01的一个平方根.
对应训练
2. 如果 3x-2 和 5x+6 都是一个非负数的平方根,
求这个非负数.
解:①若 3x-2 和 5x+6 不同,则它们互为相反数,
即 3x-2+5x+6=0,解得 x=-0.5,此时 3x-2=-3.5,
(-3.5)2=12.25.
②若 3x-2 和 5x+6 相同,则 3x-2=5x+6,
解得 x=-4,此时3x-2=5x+6=-14,(-14)2=196.
已知一个数的两个平方根,根据两个平方根互为相反数列方程求解.
综上可知,这个非负数是 12.25 或 196.
如果题目只是叙述两个数均为一个数的平方根,则需要分相反和相等两种情况进行讨论.
你会表示一个非负数的平方根吗?
即非负数 a 的平方根表示为:
非负数a
例如 .
正的平方根表示为:
负的平方根表示为:
读作“正、负根号 a”.
因为在我们所认识的数中任何一个数的平方都不会是负数,所以负数不能开平方,即当 a<0 时, 无意义.
说一说算术平方根与平方根之间的联系.
符号 只有当 a≥0 时有意义,a<0 时无意义.
你知道为什么吗?
算术平方根 平方根
区 别 概念 不同 一般地,如果一个正数 x 的平方等于 a,即 x2=a,那么这个正数 x 叫做 a 的算术平方根 一般地,如果一个数的平方等于 a,那么这个数叫做 a 的平方根
个数 不同 正数的算术平方根有_______个 正数的平方根有_______个
表示方法不同 正数 a 的算术平方根表示为_______ 正数 a 的平方根表示为_______
结果 不同 正数的算术平方根一定是_______ 正数的平方根为________,二者互为________
1
2
正数
一正一负
相反数
算术平方根 平方根
联 系 具有包含关系 同一个正数的平方根包含算术平方根,算术平方根是这个正数正的平方根 存在的条件相同 只有非负数才有平方根和算术平方根 特殊值0 0的平方根与算术平方根均为0 例 5 求下列各式的值:
(3)因为 ,所以 .
(1) ; (2) ; (3) .
解:(1)因为 62=36,所以 ;
(2)因为 0.92=0.81,所以 ;
知道一个数的算术平方根,就可以立即写出它的负的平方根. 为什么?
1. 计算下列各式的值:
【选自教材P47练习 第3题】
(1) ; (2) ; (3) .
(3)因为 ,所以 .
解:(1)因为 32=9,所以 ;
(2)因为 0.72=0.49,所以 ;
对应训练
2. 平方根概念的起源与几何中的正方形有关.
如果一个正方形的面积为 A,那么这个正方形
的边长是多少?
【选自教材P47练习 第4题】
解:正方形的边长为 .
求下列各式中 x 的值:
(1) 3x2=48; (2) (x+1)2=4; (3) 2(x-1)2-18=0.
解:(1)原式可变形为 x2=16. 因为(±4)2=16,所以 x=4 或 x=-4.
(2)因为 (±2)2=4,所以 x+1=2 或 x+1=-2,解方程,得 x=1 或 x=-3. 所以 x=1 或 x=-3.
将括号里 的内容作为一个整体
提升突破
求下列各式中 x 的值:
(1) 3x2=48; (2) (x+1)2=4; (3) 2(x-1)2-18=0.
(3)原式可变形为 (x-1)2=9. 因为(±3)2=9, 所以 x-1=3 或 x-1=-3,解方程,得x=4 或 x=-2.所以 x=4 或 x=-2.
提升突破
2. 已知 2a-1 的平方根为 ,3a-2b 的算术平方根
为 2,求 4a-b+2 的平方根.
解:因为 2a-1 的平方根为 ,所以 2a-1=3,解得 a=2.
因为 3a-2b 的算术平方根为 2,所以 3a-2b=4,所以 6-2b=4,解得 b=1.
所以 4a-b+2=9.
因为 9 的平方根为 ±3,所以 4a-b+2 的平方根为 ±3.
求下列各式中 x 的值:
(1) 4x2-1=0; (2) (x+1)2=81; (3) (2x-3)2-64=0.
(2)因为 (±9)2=81,所以 x+1=9 或 x+1=-9,解方程,得 x=8 或 x=-10. 所以 x=8 或 x=-10.
解:(1)原式可变形为 . 因为 ,所以 或 .
对应训练
求下列各式中 x 的值:
(1) 4x2-1=0; (2) (x+1)2=81; (3) (2x-3)2-64=0.
(3)原式可变形为 (2x-3)2=64.
因为(±8)2=64,所以 2x-3=8 或 2x-3=-8,
解方程,得 或 . 所以 或 .
对应训练
2. 一个数的算术平方根为 2a-6,平方根为 ±(a-1),
求 a 的值与这个数.
解:分两种情况:
① 当 2a-6=a-1 时,可得 a=5,此时 2a-6=4,42=16;
所以 a 的值为5,这个数为16.
② 当2a-6=-(a-1) 时,可得 a= ,此时 2a-6=- , 不符合题意,此种情况不存在.
1. 求下列各数的平方根:
【选自教材P47习题6.1 第3题】
(1)49;(2) ;(3) ;(4)0.0016 .
±7
0.04
随堂训练
2. 判断下列说法是否正确:
【选自教材P47习题6.1 第4题】
(1)5 是 25 的算术平方根;
(2) 的一个平方根;
(3)(-4)2的平方根是 -4;
(4)0 的平方根与算术平方根都是 0.
3. 根据下表回答下列问题:
【选自教材P48习题6.1 第7题】
x 16 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 17
x2 256 259.21 262.44 265.69 268.96 272.25 275.56 278.89 282.24 285.61 289
(1)268.96的平方根是多少?
(2) _________.
(3) 在表中哪两个相邻的数之间?为什么?
±16.4
16.9
解:在 16.4 与 16.5 之间.
因为 16.42<270<16.52,所以16.4< <16.5.
4. 一个正方形的面积扩大为原来的 4 倍,它的边长
变为原来的多少倍?面积扩大为原来的 9 倍呢?
n 倍呢?
【选自教材P48习题6.1 第10题】
解:面积扩大为原来的 4 倍,它的边长变为原来的 2 倍.
面积扩大为原来的 9 倍,它的边长变为原来的 3 倍.
面积扩大为原来的 n 倍,边长变为原来的 倍.
课堂小结
互为
逆运算
平方
表示
如果一个数的平方等于 a,那么这个数叫做 a 的________或二次方根.
正数 a 的平方根是_____;0 的平方根是_______; 负数没有平方根
平方根
定义
性质
开平方
平方根
0
正数 a 的平方根有两个,它们互为_______;
表示_____________,
表示_____________.
相反数
a 的正平方根
a 的负平方根
课后作业
完成对应课时的练习.
本章概览
乘方
开方
平方根
立方根
实数
实数的概念及性质
实数的大小比较与运算
互为
逆运算
开平方
开立方
平方根
算术 平方根
算术平方根的估算
平方根
平方根
人教版七年级下册
第3课时 平方根
第六章 实数
6.1 平方根
1. 一般地,如果一个_______的平方等于 a,即 x2=a,那么这个_______叫做 a 的算术平方根.
2. 填空:(1)22=_____,(-2)2=_____;
(2)0.82=_____,(-0.8)2=_____.
3. 想一想:5的平方等于25,5叫做25的算术平方根. -5的平方也等于25,那么-5叫做25的什么根呢?
正数x
4
4
0.64
正数x
0.64
复习回顾
思考
如果一个数的平方等于9,这个数是多少?
32=9,这个数可以是 3.
(-3)2=9,这个数也可以是 -3.
因此,如果一个数的平方等于9,那么这个数是 3 或 -3.
想一想: 3和-3有什么特征?
3 和 -3 互 为相反数,会不会是 巧合呢?
互为相反数,3和-3一起叫做±3.
x2 1 16 0 49
x
填表:
±1
±4
0
±7
如果我们把上述填表的 x 的值分别叫做1,16,0,49, 的平方根,你能类比算术平方根的概念,给出平方根的概念吗?
探究新知
概念
引入
一般地,如果一个数的平方等于 a,那么这个数叫做 a 的平方根或二次方根. 这就是说,如果 x2=a,那么 x 叫做 a 的平方根.
平方根
二次方根
例如,3 和 -3 是 9 的平方根,
简记为±3是 9 的平方根.
你还能再举几个平方根的例子吗?
求一个数 a 的平方根的运算,叫做开平方.
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
观察下图,你发现了什么?
平方
开平方
互为逆运算
归纳
小结
平方根的概念和计算
如果 x2=a,那么 x 叫做 a 的平方根.
平方与开平方互为逆运算.
根据这种互逆关系,可以求一个数的平方根.
互为 逆运算
平方运算
开平方运算
例 4 求下列各数的平方根:
(1)100; (2) ; (3)0.25.
解:(1)因为(±10)2=100,所以100的平方根是±10;
(2)因为 ,所以 的平方根是± ;
(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
x 8 -8
x2 16 0.36 1. 填表:
64
4
-4
0.6
-0.6
【选自教材P47练习 第2题】
对应训练
2. 求下列各数的平方根:
(1)64;(2)0.09;(3) ;(4)(-7)2.
解:(1)因为(±8)2=64,所以64的平方根是±8;
(3)因为 ,所以 的平方根是± ;
(4)因为(±7)2=(-7)2=49,所以(-7)2的平方根
是±7.
(2)因为(±0.3)2=0.09,所以0.09的平方根是±0.3;
思考
1,4,9的平方根分别是多少?
正数的平方根有什么特点?
1,4,9的平方根分别是±1,±2,±3.
正数有两个平方根,它们互为相反数,其中正的平方根就是这个数的算术平方根.
0有几个平方根?各是多少?为什么?
0 只有一个平方根,是 0. 因为 02=0,并且任何一个不为 0 的数的平方都不等于 0,所以 0 的平方根是 0.
思考
-1,-4,-9有平方根吗?为什么?
没有. 正数的平方是正数,0 的平方是 0,负数的平方也是正数,即在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根.
归 纳
正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
1. 判断下列说法是否正确:
【选自教材P46练习 第1题】
(1)0的平方根是0;
(2)1的平方根是1;
(3)-1的平方根是-1;
(4)0.01是0.1的一个平方根.
1的平方根是±1.
-1没有平方根.
0.1是0.01的一个平方根.
对应训练
2. 如果 3x-2 和 5x+6 都是一个非负数的平方根,
求这个非负数.
解:①若 3x-2 和 5x+6 不同,则它们互为相反数,
即 3x-2+5x+6=0,解得 x=-0.5,此时 3x-2=-3.5,
(-3.5)2=12.25.
②若 3x-2 和 5x+6 相同,则 3x-2=5x+6,
解得 x=-4,此时3x-2=5x+6=-14,(-14)2=196.
已知一个数的两个平方根,根据两个平方根互为相反数列方程求解.
综上可知,这个非负数是 12.25 或 196.
如果题目只是叙述两个数均为一个数的平方根,则需要分相反和相等两种情况进行讨论.
你会表示一个非负数的平方根吗?
即非负数 a 的平方根表示为:
非负数a
例如 .
正的平方根表示为:
负的平方根表示为:
读作“正、负根号 a”.
因为在我们所认识的数中任何一个数的平方都不会是负数,所以负数不能开平方,即当 a<0 时, 无意义.
说一说算术平方根与平方根之间的联系.
符号 只有当 a≥0 时有意义,a<0 时无意义.
你知道为什么吗?
算术平方根 平方根
区 别 概念 不同 一般地,如果一个正数 x 的平方等于 a,即 x2=a,那么这个正数 x 叫做 a 的算术平方根 一般地,如果一个数的平方等于 a,那么这个数叫做 a 的平方根
个数 不同 正数的算术平方根有_______个 正数的平方根有_______个
表示方法不同 正数 a 的算术平方根表示为_______ 正数 a 的平方根表示为_______
结果 不同 正数的算术平方根一定是_______ 正数的平方根为________,二者互为________
1
2
正数
一正一负
相反数
算术平方根 平方根
联 系 具有包含关系 同一个正数的平方根包含算术平方根,算术平方根是这个正数正的平方根 存在的条件相同 只有非负数才有平方根和算术平方根 特殊值0 0的平方根与算术平方根均为0 例 5 求下列各式的值:
(3)因为 ,所以 .
(1) ; (2) ; (3) .
解:(1)因为 62=36,所以 ;
(2)因为 0.92=0.81,所以 ;
知道一个数的算术平方根,就可以立即写出它的负的平方根. 为什么?
1. 计算下列各式的值:
【选自教材P47练习 第3题】
(1) ; (2) ; (3) .
(3)因为 ,所以 .
解:(1)因为 32=9,所以 ;
(2)因为 0.72=0.49,所以 ;
对应训练
2. 平方根概念的起源与几何中的正方形有关.
如果一个正方形的面积为 A,那么这个正方形
的边长是多少?
【选自教材P47练习 第4题】
解:正方形的边长为 .
求下列各式中 x 的值:
(1) 3x2=48; (2) (x+1)2=4; (3) 2(x-1)2-18=0.
解:(1)原式可变形为 x2=16. 因为(±4)2=16,所以 x=4 或 x=-4.
(2)因为 (±2)2=4,所以 x+1=2 或 x+1=-2,解方程,得 x=1 或 x=-3. 所以 x=1 或 x=-3.
将括号里 的内容作为一个整体
提升突破
求下列各式中 x 的值:
(1) 3x2=48; (2) (x+1)2=4; (3) 2(x-1)2-18=0.
(3)原式可变形为 (x-1)2=9. 因为(±3)2=9, 所以 x-1=3 或 x-1=-3,解方程,得x=4 或 x=-2.所以 x=4 或 x=-2.
提升突破
2. 已知 2a-1 的平方根为 ,3a-2b 的算术平方根
为 2,求 4a-b+2 的平方根.
解:因为 2a-1 的平方根为 ,所以 2a-1=3,解得 a=2.
因为 3a-2b 的算术平方根为 2,所以 3a-2b=4,所以 6-2b=4,解得 b=1.
所以 4a-b+2=9.
因为 9 的平方根为 ±3,所以 4a-b+2 的平方根为 ±3.
求下列各式中 x 的值:
(1) 4x2-1=0; (2) (x+1)2=81; (3) (2x-3)2-64=0.
(2)因为 (±9)2=81,所以 x+1=9 或 x+1=-9,解方程,得 x=8 或 x=-10. 所以 x=8 或 x=-10.
解:(1)原式可变形为 . 因为 ,所以 或 .
对应训练
求下列各式中 x 的值:
(1) 4x2-1=0; (2) (x+1)2=81; (3) (2x-3)2-64=0.
(3)原式可变形为 (2x-3)2=64.
因为(±8)2=64,所以 2x-3=8 或 2x-3=-8,
解方程,得 或 . 所以 或 .
对应训练
2. 一个数的算术平方根为 2a-6,平方根为 ±(a-1),
求 a 的值与这个数.
解:分两种情况:
① 当 2a-6=a-1 时,可得 a=5,此时 2a-6=4,42=16;
所以 a 的值为5,这个数为16.
② 当2a-6=-(a-1) 时,可得 a= ,此时 2a-6=- , 不符合题意,此种情况不存在.
1. 求下列各数的平方根:
【选自教材P47习题6.1 第3题】
(1)49;(2) ;(3) ;(4)0.0016 .
±7
0.04
随堂训练
2. 判断下列说法是否正确:
【选自教材P47习题6.1 第4题】
(1)5 是 25 的算术平方根;
(2) 的一个平方根;
(3)(-4)2的平方根是 -4;
(4)0 的平方根与算术平方根都是 0.
3. 根据下表回答下列问题:
【选自教材P48习题6.1 第7题】
x 16 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 17
x2 256 259.21 262.44 265.69 268.96 272.25 275.56 278.89 282.24 285.61 289
(1)268.96的平方根是多少?
(2) _________.
(3) 在表中哪两个相邻的数之间?为什么?
±16.4
16.9
解:在 16.4 与 16.5 之间.
因为 16.42<270<16.52,所以16.4< <16.5.
4. 一个正方形的面积扩大为原来的 4 倍,它的边长
变为原来的多少倍?面积扩大为原来的 9 倍呢?
n 倍呢?
【选自教材P48习题6.1 第10题】
解:面积扩大为原来的 4 倍,它的边长变为原来的 2 倍.
面积扩大为原来的 9 倍,它的边长变为原来的 3 倍.
面积扩大为原来的 n 倍,边长变为原来的 倍.
课堂小结
互为
逆运算
平方
表示
如果一个数的平方等于 a,那么这个数叫做 a 的________或二次方根.
正数 a 的平方根是_____;0 的平方根是_______; 负数没有平方根
平方根
定义
性质
开平方
平方根
0
正数 a 的平方根有两个,它们互为_______;
表示_____________,
表示_____________.
相反数
a 的正平方根
a 的负平方根
课后作业
完成对应课时的练习.
