最新人教版七下数学 6.3 实数 第1课时 实数的概念 课件(共33张PPT)
文档属性
| 名称 | 最新人教版七下数学 6.3 实数 第1课时 实数的概念 课件(共33张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 11:31:25 | ||
图片预览







文档简介
(共33张PPT)
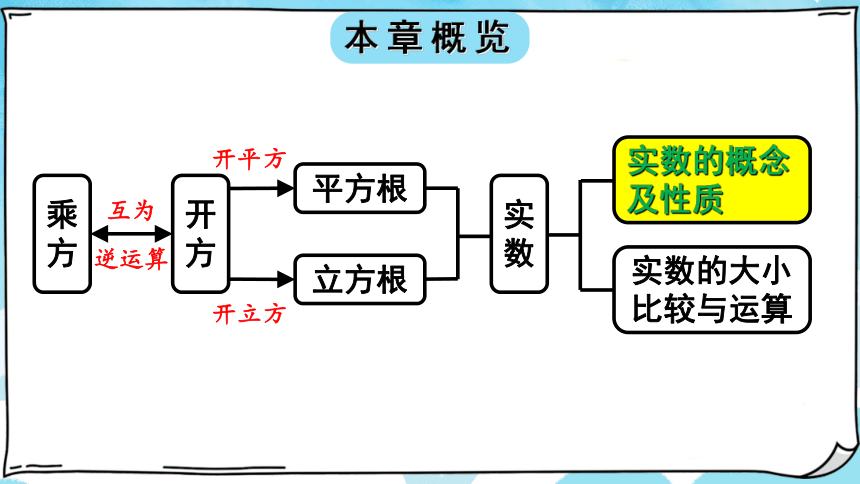
本章概览
乘方
开方
平方根
立方根
实数
实数的概念及性质
实数的大小比较与运算
互为
逆运算
开平方
开立方
6.3 实数
人教版七年级(下)
第1课时 实数的概念
复习导入
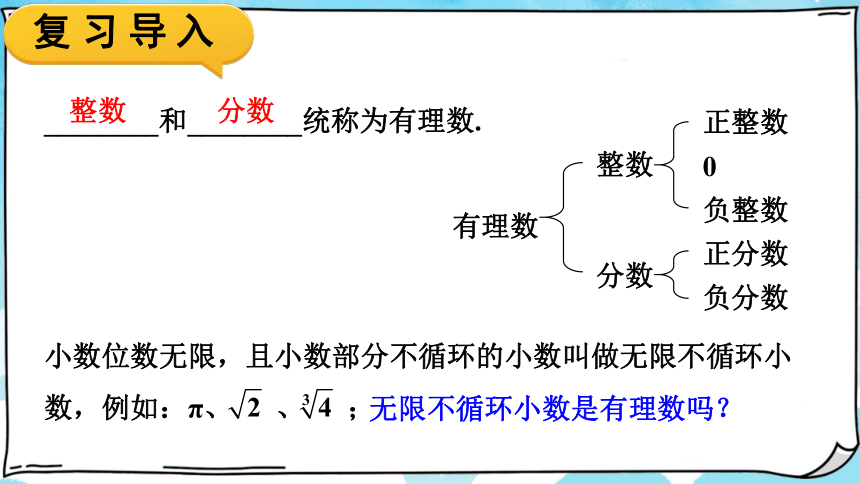
________和________统称为有理数.
小数位数无限,且小数部分不循环的小数叫做无限不循环小数,例如:π、 、 ;
无限不循环小数是有理数吗?
整数
分数
有理数
整数
分数
正整数
0
负整数
正分数
负分数
新课探究
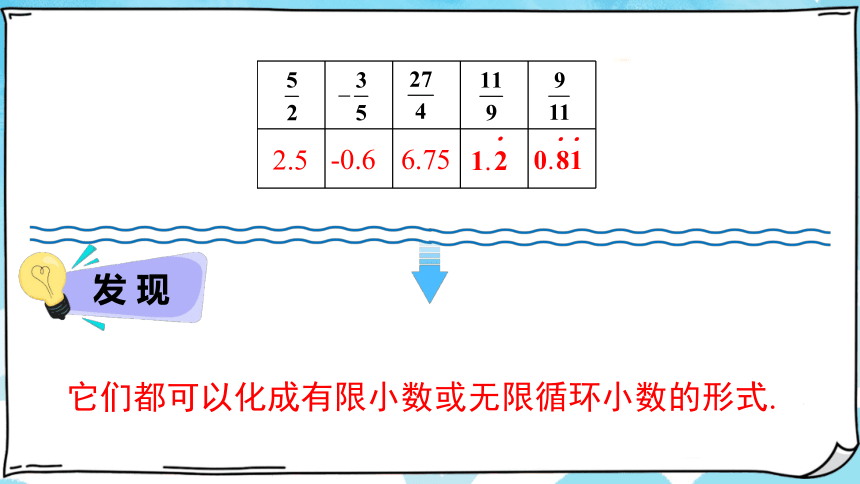
问题 我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
探究点1 实数的概念及分类
它们都可以化成有限小数或无限循环小数的形式.
发 现
-1 0
2.5
-0.6
6.75
-1.0
0.0
-1 0 π
-1.0
0.0
2.5
-0.6
6.75
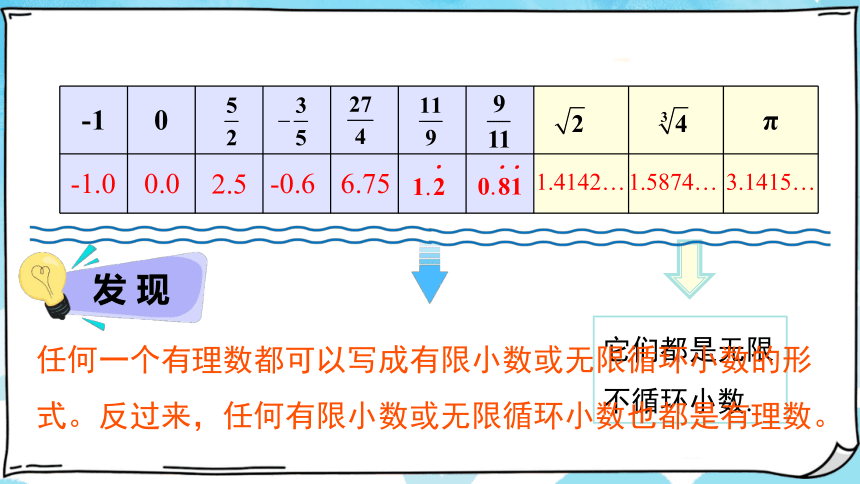
1.4142…
1.5874…
3.1415…
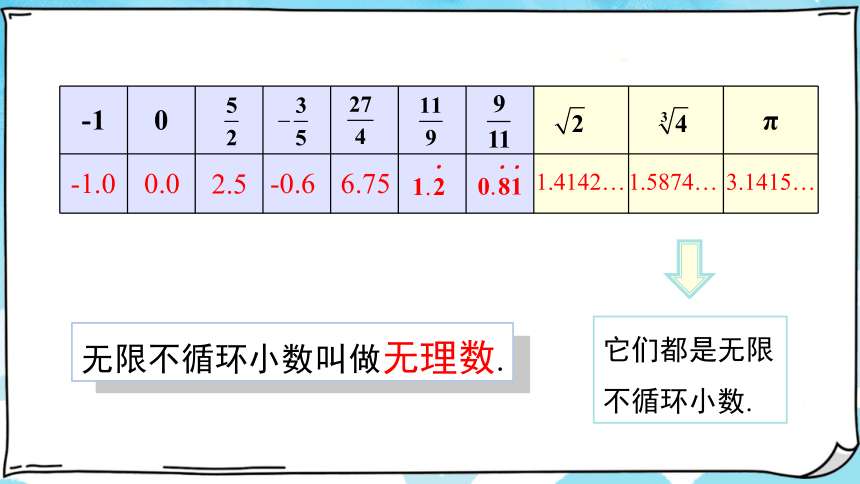
它们都是无限不循环小数.
发 现
任何一个有理数都可以写成有限小数或无限循环小数的形式。反过来,任何有限小数或无限循环小数也都是有理数。
-1 0 π
-1.0
0.0
2.5
-0.6
6.75
1.4142…
1.5874…
3.1415…
无限不循环小数叫做无理数.
它们都是无限不循环小数.
思考: 是无理数吗?2.020 020 002 000 02…是无
理数吗?
2.02002000200002…
无限不循环小数.
是无理数
常见的无理数的形式:
(1)开方开不尽的数,如 , 等;
(2)π及化简后含有π的式子,如π,2-π等;
(3)有特殊特征的数,如1.212212 221…(相邻的两个1之间依次多一个2)等;
(4)有理数和无理数的和、差,如 , 等.
有理数与无理数的区别:
有理数 无理数
是有限小数或无限循环小数
是无限不循环小数
都能写成分数的行书(正数可以看成分母是1的分数)
不能写成分数的形式
有理数
整数
自然数
负数
分数
无理数
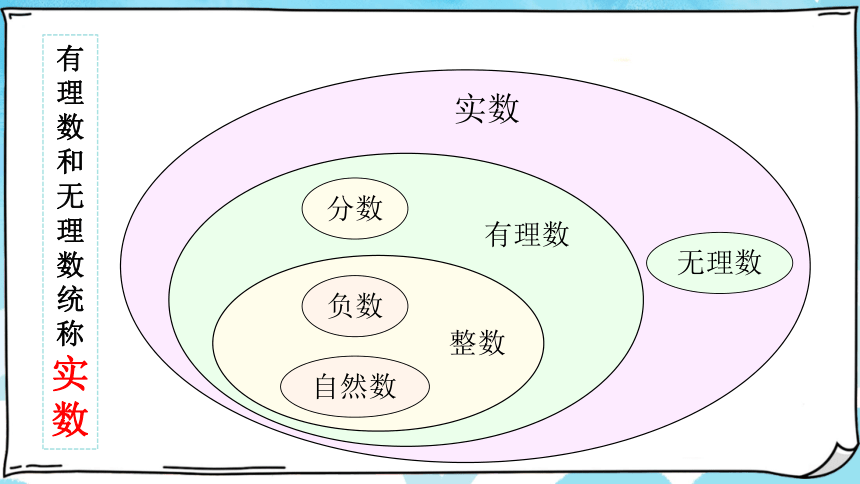
实数
有理数和无理数统称实数
思考:
仿照有理数的分类,你能对实数进行分类吗?
按概念分
按大小分
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
按概念分
负实数
正实数
数实
正有理数
负有理数
0
正无理数
负无理数
按大小分
实数分类的原则:
分类可以有不同的方法,但要按同一标准,不重复不遗漏。
1.下列说法中,正确的是( ).
A. 实数分为正实数和负实数
B. 无限小数都是无理数
C. 无理数都是无限小数
D. 带根号的数都是无理数
C
<针对训练>
正 负
和0
无限循环小数是有理数
无理数:
有理数:
正实数:
负实数:
2.将下列各数分别填入下列相应的括号内:
思考:每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴于的点来表示呢 你能在数轴上找到表示无理数的点吗?
小组合作交流:
在数轴上找出表示π、 和 的点,说一说你是怎么找的.
探究点2 实数与数轴上的点的对应关系
0
-1
1
3
2
4
●
因为半径为 1 的圆的周长为 π,所以数轴上点 A 表示的数是无理数 π.
●
●
●
●
●
●
●
●
●
●
●
●
●
几何画板
A
-1
-2
0
2
1
3
用两个面积为1的小正方形剪拼成一个面积为2的大正方形,这个大正方形的边长就是小正方形的对角线长,因此以原点为圆心,以小正方形的对角线为半径画弧,与数轴的两个交点分别表示数 和 .
当数的范围从有理数扩充到实数后,实数与数轴上的点是___________的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个_______.
一一对应
实数
实数
数轴上的点
一一对应
请将图中数轴上标有字母的各点与下列实数对应起来:
【教材P56 练习 第1题】
<针对训练>
思考:无理数也有相反数和绝对值吗?怎么表示?
相反数 绝对值
有理数 2
0
无理数
-π
5.41441…
-2
2
0
0
π
π
-5.41441…
5.41441…
探究点3 实数的相反数、绝对值
相反数 绝对值
定义
a(a是实数) a>0
a=0
a<0
实数a到原点的距离
只有符号不同的两个实数互为相反数
-a
a
0
-a
你能得出实数的相反数和绝对值的意义吗?
例1
(1)分别写出 的相反数;
(2)分别指出 分别是什么数的相反数;
【教材P55 例1】
相反数
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
例1
【教材P55 例1】
绝对值
1. 下列说法正确的是( )
A.带根号的数和分数统称实数
B.正实数包括正有理数和正无理数
C.实数包括正实数和负实数
D.无理数包括正无理数、负无理数和0
B
随堂训练
2. 求下列各数的相反数与绝对值:
【教材P56 练习 第2题】
相反数:
绝对值:
-2.5
2.5
0
0
3. 求下列各式中的实数x:
【教材P56 练习 第3题】
0
-1
-2
-3
4. 在数轴上画出表示 的点.
解:以单位长度为边长画一个正方形如图,以 -1 为圆心,正方形的对角线为半径画弧,与负半轴的交点就表示点 .
5. 如图,在数轴上点A表示数a,点B表示数b,且a,b满足|a+3|十(b-6)2=0.
(1)点A表示的数为______,点B表示的数为______;
(2)若点C表示的数的绝对值为 ,求点C到点B的距离.
-3
6
解:若点C表示的数的绝对值为 ,则点C表示的数为 或 ,
当点C表示的数为 时,点C到点B的距离为 ;
当点C表示的数为 时,点C到点B的距离为 .
6. 若实数 a,b 互为相反数,c,d 互为倒数,m 是 9 的平方根. 求 的值.
当 m = 3 时,原式 = 0 + 1 + (3 - 1)2 = 1 + 4 = 5;
当 m = -3 时,
原式 = 0 + 1 + (-3 - 1)2 = 1 + 16 = 17.
解:由已知得 a + b = 0,cd = 1,m = ±3.
实数
概念
分类
实数的相反数、绝对值的意义
实数与数轴上的点一一对应
无限不循环小数又叫做无理数.有理数和无理数统称实数
有理数
无理数
正有理数
负有理数
正无理数
负无理数
有限小数或无线循环小数
无限不循环小数
0
课堂小结
开方开不尽的数
π
有规律不循环的数
本章概览
乘方
开方
平方根
立方根
实数
实数的概念及性质
实数的大小比较与运算
互为
逆运算
开平方
开立方
6.3 实数
人教版七年级(下)
第1课时 实数的概念
复习导入
________和________统称为有理数.
小数位数无限,且小数部分不循环的小数叫做无限不循环小数,例如:π、 、 ;
无限不循环小数是有理数吗?
整数
分数
有理数
整数
分数
正整数
0
负整数
正分数
负分数
新课探究
问题 我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
探究点1 实数的概念及分类
它们都可以化成有限小数或无限循环小数的形式.
发 现
-1 0
2.5
-0.6
6.75
-1.0
0.0
-1 0 π
-1.0
0.0
2.5
-0.6
6.75
1.4142…
1.5874…
3.1415…
它们都是无限不循环小数.
发 现
任何一个有理数都可以写成有限小数或无限循环小数的形式。反过来,任何有限小数或无限循环小数也都是有理数。
-1 0 π
-1.0
0.0
2.5
-0.6
6.75
1.4142…
1.5874…
3.1415…
无限不循环小数叫做无理数.
它们都是无限不循环小数.
思考: 是无理数吗?2.020 020 002 000 02…是无
理数吗?
2.02002000200002…
无限不循环小数.
是无理数
常见的无理数的形式:
(1)开方开不尽的数,如 , 等;
(2)π及化简后含有π的式子,如π,2-π等;
(3)有特殊特征的数,如1.212212 221…(相邻的两个1之间依次多一个2)等;
(4)有理数和无理数的和、差,如 , 等.
有理数与无理数的区别:
有理数 无理数
是有限小数或无限循环小数
是无限不循环小数
都能写成分数的行书(正数可以看成分母是1的分数)
不能写成分数的形式
有理数
整数
自然数
负数
分数
无理数
实数
有理数和无理数统称实数
思考:
仿照有理数的分类,你能对实数进行分类吗?
按概念分
按大小分
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
按概念分
负实数
正实数
数实
正有理数
负有理数
0
正无理数
负无理数
按大小分
实数分类的原则:
分类可以有不同的方法,但要按同一标准,不重复不遗漏。
1.下列说法中,正确的是( ).
A. 实数分为正实数和负实数
B. 无限小数都是无理数
C. 无理数都是无限小数
D. 带根号的数都是无理数
C
<针对训练>
正 负
和0
无限循环小数是有理数
无理数:
有理数:
正实数:
负实数:
2.将下列各数分别填入下列相应的括号内:
思考:每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴于的点来表示呢 你能在数轴上找到表示无理数的点吗?
小组合作交流:
在数轴上找出表示π、 和 的点,说一说你是怎么找的.
探究点2 实数与数轴上的点的对应关系
0
-1
1
3
2
4
●
因为半径为 1 的圆的周长为 π,所以数轴上点 A 表示的数是无理数 π.
●
●
●
●
●
●
●
●
●
●
●
●
●
几何画板
A
-1
-2
0
2
1
3
用两个面积为1的小正方形剪拼成一个面积为2的大正方形,这个大正方形的边长就是小正方形的对角线长,因此以原点为圆心,以小正方形的对角线为半径画弧,与数轴的两个交点分别表示数 和 .
当数的范围从有理数扩充到实数后,实数与数轴上的点是___________的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个_______.
一一对应
实数
实数
数轴上的点
一一对应
请将图中数轴上标有字母的各点与下列实数对应起来:
【教材P56 练习 第1题】
<针对训练>
思考:无理数也有相反数和绝对值吗?怎么表示?
相反数 绝对值
有理数 2
0
无理数
-π
5.41441…
-2
2
0
0
π
π
-5.41441…
5.41441…
探究点3 实数的相反数、绝对值
相反数 绝对值
定义
a(a是实数) a>0
a=0
a<0
实数a到原点的距离
只有符号不同的两个实数互为相反数
-a
a
0
-a
你能得出实数的相反数和绝对值的意义吗?
例1
(1)分别写出 的相反数;
(2)分别指出 分别是什么数的相反数;
【教材P55 例1】
相反数
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
例1
【教材P55 例1】
绝对值
1. 下列说法正确的是( )
A.带根号的数和分数统称实数
B.正实数包括正有理数和正无理数
C.实数包括正实数和负实数
D.无理数包括正无理数、负无理数和0
B
随堂训练
2. 求下列各数的相反数与绝对值:
【教材P56 练习 第2题】
相反数:
绝对值:
-2.5
2.5
0
0
3. 求下列各式中的实数x:
【教材P56 练习 第3题】
0
-1
-2
-3
4. 在数轴上画出表示 的点.
解:以单位长度为边长画一个正方形如图,以 -1 为圆心,正方形的对角线为半径画弧,与负半轴的交点就表示点 .
5. 如图,在数轴上点A表示数a,点B表示数b,且a,b满足|a+3|十(b-6)2=0.
(1)点A表示的数为______,点B表示的数为______;
(2)若点C表示的数的绝对值为 ,求点C到点B的距离.
-3
6
解:若点C表示的数的绝对值为 ,则点C表示的数为 或 ,
当点C表示的数为 时,点C到点B的距离为 ;
当点C表示的数为 时,点C到点B的距离为 .
6. 若实数 a,b 互为相反数,c,d 互为倒数,m 是 9 的平方根. 求 的值.
当 m = 3 时,原式 = 0 + 1 + (3 - 1)2 = 1 + 4 = 5;
当 m = -3 时,
原式 = 0 + 1 + (-3 - 1)2 = 1 + 16 = 17.
解:由已知得 a + b = 0,cd = 1,m = ±3.
实数
概念
分类
实数的相反数、绝对值的意义
实数与数轴上的点一一对应
无限不循环小数又叫做无理数.有理数和无理数统称实数
有理数
无理数
正有理数
负有理数
正无理数
负无理数
有限小数或无线循环小数
无限不循环小数
0
课堂小结
开方开不尽的数
π
有规律不循环的数
