青岛版七年级数学下册第8章8.5垂直同步训练题(含答案)
文档属性
| 名称 | 青岛版七年级数学下册第8章8.5垂直同步训练题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 89.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-25 21:49:26 | ||
图片预览

文档简介
青岛版七年级数学下册第8章8.5垂直同步训练题(含答案)
一.选择题(共10小题)
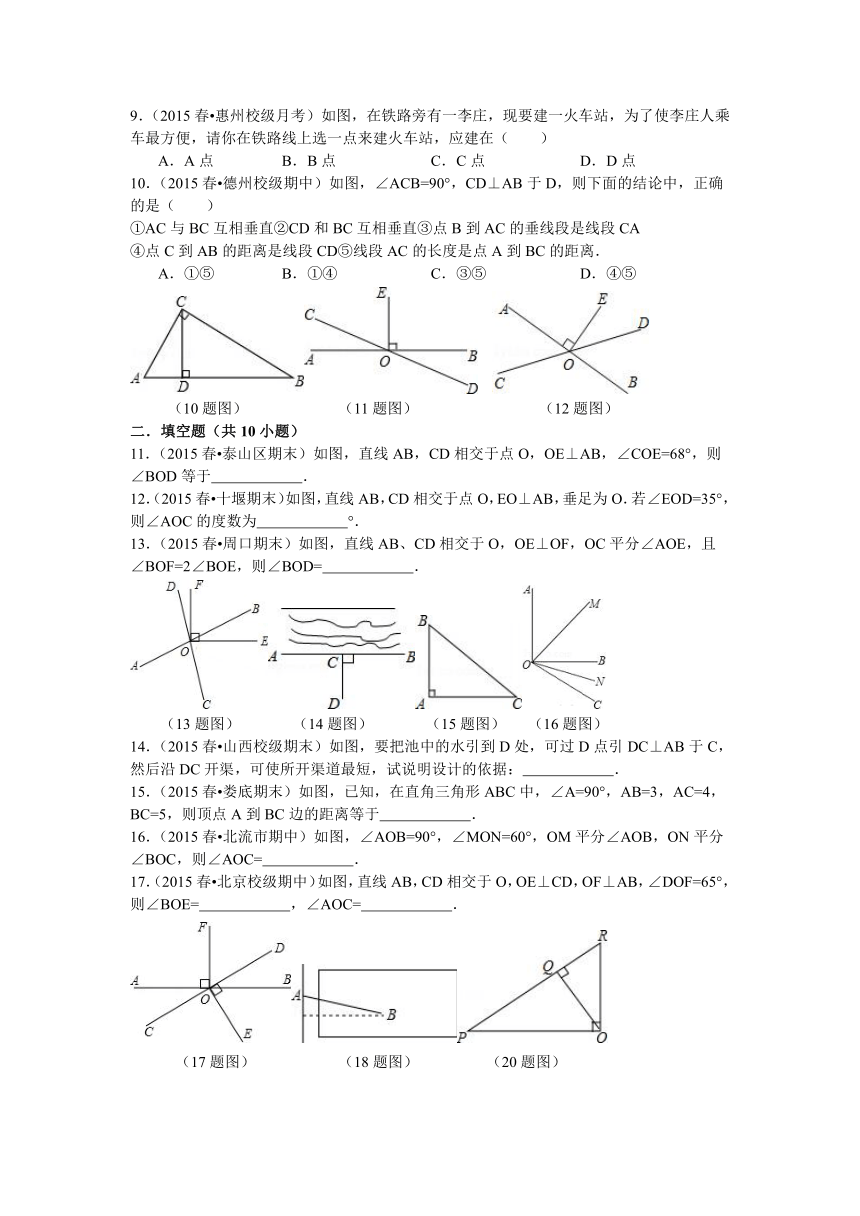
1.(2015春 荔城区期末)如图,直线PQ⊥MN,垂足为O,AB是过点O的直线,∠1=50°,则∠2的度数为( )
A.50° B. 40° C. 60° D. 70°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1题图) (2题图) (3题图) (5题图)
2.(2015 厦门)如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长 B. 线段CD的长 C. 线段AD的长 D. 线段AB的长
3.(2015 河北模拟)如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B. 45° C. 55° D. 65°
4.(2015春 巴南区校级期末)下列说法中正确的个数有( )
(1)直线外一点与直线上各点连接的所有线段中,垂线段最短.
(2)画一条直线的垂线段可以画无数条.
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直.
(4)从直线外一点到这条直线的垂线段叫做点到直线的距离.
A.1个 B. 2个 C. 3个 D. 4个
5.(2015春 泰山区期末)如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
A.34° B. 44° C. 54° D. 64°
6.(2015春 重庆校级期中)如图,点O在直线AC上,BO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B. 45° C. 55° D. 65°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(6题图) (7题图) (9题图)
7.(2015春 连江县期中)如图,在一 ( http: / / www.21cnjy.com )张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )
A.0条 B. 1条 C. 2条 D. 无数条
8.(2015春 凉山州期末)体育课上,老师测量小明跳远成绩的依据是( )
A. 过直线上一点且垂直于这条直线的直线有且只有一条
B. 两点之间,线段最短
C. 垂线段最短 D. 两点确定一条直线
9.(2015春 惠州校级月考)如图,在铁 ( http: / / www.21cnjy.com )路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B. B点 C. C点 D. D点
10.(2015春 德州校级期中)如图,∠ACB=90°,CD⊥AB于D,则下面的结论中,正确的是( )
①AC与BC互相垂直②CD和BC互相垂直③点B到AC的垂线段是线段CA
④点C到AB的距离是线段CD⑤线段AC的长度是点A到BC的距离.
A.①⑤ B. ①④ C. ③⑤ D. ④⑤
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(10题图) (11题图) (12题图)
二.填空题(共10小题)
11.(2015春 泰山区期末)如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD等于 .
12.(2015春 十堰期末)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.若∠EOD=35°,则∠AOC的度数为 °.
13.(2015春 周口期末)如图,直线A ( http: / / www.21cnjy.com )B、CD相交于O,OE⊥OF,OC平分∠AOE,且∠BOF=2∠BOE,则∠BOD= .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(13题图) (14题图) (15题图) (16题图)
14.(2015春 山西校 ( http: / / www.21cnjy.com )级期末)如图,要把池中的水引到D处,可过D点引DC⊥AB于C,然后沿DC开渠,可使所开渠道最短,试说明设计的依据: .
15.(2015春 娄底期末)如图,已 ( http: / / www.21cnjy.com )知,在直角三角形ABC中,∠A=90°,AB=3,AC=4,BC=5,则顶点A到BC边的距离等于 .
16.(2015春 北流市期中)如图,∠AOB=90°,∠MON=60°,OM平分∠AOB,ON平分∠BOC,则∠AOC= .
17.(2015春 北京校级期中) ( http: / / www.21cnjy.com )如图,直线AB,CD相交于O,OE⊥CD,OF⊥AB,∠DOF=65°,则∠BOE= ,∠AOC= .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(17题图) (18题图) (20题图)
18.(2015春 保定期末)如图 ( http: / / www.21cnjy.com ),立定跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离 4.6米.(填“大于”“小于”或“等于”)
19.(2015春 吉州区期末)在下列说法中 ( http: / / www.21cnjy.com ):①两点确定一条直线;②垂线段最短;③相等的角是对顶角;④三角形三条高、中线、角平分线都分别交于一点,正确的有 .(只填序号)
20.(2015春 揭西县校级月考)如图,PO⊥OR,OQ⊥PR,则点O到PR的所在的直线的距离是 的长.
三.解答题(共5小题)
21.(2015春 会宁县期中)如图,∠1=30°,AB⊥CD,垂足为O,EF经过点O.求∠2、∠3的度数.
( http: / / www.21cnjy.com )
22.(2015春 湖北校 ( http: / / www.21cnjy.com )级期中)如图,直线AB、CD相交于O点,∠AOC与∠AOD的度数比为4:5,OE⊥AB,OF平分∠DOB,求∠EOF的度数.
( http: / / www.21cnjy.com )
23.(2015春 淄博校级期中)如图所示,OA⊥OB,OC⊥OD,OE为∠BOD的平分线,∠BOE=17°.求∠AOC的度数.
( http: / / www.21cnjy.com )
24.(2015春 龙口市期中)如图:AB、CD、EF交于O点,AB⊥CD,OG平分∠AOE,∠COE=28°,求∠AOG的度数.
( http: / / www.21cnjy.com )
25.(2015春 连江 ( http: / / www.21cnjy.com )县期中)如图:直线AB,CD相交于点O,EO⊥AB,垂足为O,OF平分∠BOD,∠BOF=15°,求∠COE的度数.
( http: / / www.21cnjy.com )
青岛版七年级数学下册第8章8.5垂直同步训练题参考答案
一.选择题(共10小题)
1.B 2.B 3.C 4.C 5.B 6.C 7.B 8.C 9.A 10.A二.填空题(共10小题)
11.22° 12.55° 13.75° 14.垂线段最短 15.2.4 16.120°
17.65°25° 18.大于 19.①② 20.OQ
三.解答题(共5小题)
21.解:由题意得:
∠3=∠1=30°(对顶角相等)
∵AB⊥CD(已知)
∴∠BOD=90°(垂直的定义)
∴∠3+∠2=90°
即30°+∠2=90°
∴∠2=60°
22.解:设∠AOC=4x,则∠AOD=5x,
∵∠AOC+∠AOD=180°,∴4x+5x=180°,解得x=20°,
∴∠AOC=4x=80°,
∴∠BOD=80°,
∵OE⊥AB,∴∠BOE=90°,
∴∠DOE=∠BOE﹣∠BOD=10°,
又∵OF平分∠DOB,
∴∠DOF=∠BOD=40°,
∴∠EOF=∠EOD+∠DOF=10°+40°=50°.
23.解:∵OA⊥OB,OC⊥OD,∴∠AOB=∠COD=90°,
∵OE为∠BOD的平分线,∠BOE=17°,
∴∠BOD=2∠BOE=34°,
∴∠AOC=360°﹣90°﹣90°﹣34°=146°.
24.解:∵AB⊥CD,∴∠AOC=90°.
∵∠FOD与∠BOE是对顶角,∴∠COE=∠FOD=28°,
∴∠BOE=90°﹣∠COE=62°,
∴∠AOE=180°﹣62°=118°,
∵OG平分∠AOE,
∴∠AOG=∠AOE=×118°=59°.
25.解:∵OF平分∠BOD,∠BOF=15°,∴∠BOD=2∠BOF=30°,
∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=30°,
∵EO⊥AB,
∴∠AOC+∠COE=90°,
∴∠COE=90°﹣∠AOC=90°﹣30°=60°.
一.选择题(共10小题)
1.(2015春 荔城区期末)如图,直线PQ⊥MN,垂足为O,AB是过点O的直线,∠1=50°,则∠2的度数为( )
A.50° B. 40° C. 60° D. 70°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1题图) (2题图) (3题图) (5题图)
2.(2015 厦门)如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长 B. 线段CD的长 C. 线段AD的长 D. 线段AB的长
3.(2015 河北模拟)如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B. 45° C. 55° D. 65°
4.(2015春 巴南区校级期末)下列说法中正确的个数有( )
(1)直线外一点与直线上各点连接的所有线段中,垂线段最短.
(2)画一条直线的垂线段可以画无数条.
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直.
(4)从直线外一点到这条直线的垂线段叫做点到直线的距离.
A.1个 B. 2个 C. 3个 D. 4个
5.(2015春 泰山区期末)如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
A.34° B. 44° C. 54° D. 64°
6.(2015春 重庆校级期中)如图,点O在直线AC上,BO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B. 45° C. 55° D. 65°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(6题图) (7题图) (9题图)
7.(2015春 连江县期中)如图,在一 ( http: / / www.21cnjy.com )张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线,能折出这样的直线的条数为( )
A.0条 B. 1条 C. 2条 D. 无数条
8.(2015春 凉山州期末)体育课上,老师测量小明跳远成绩的依据是( )
A. 过直线上一点且垂直于这条直线的直线有且只有一条
B. 两点之间,线段最短
C. 垂线段最短 D. 两点确定一条直线
9.(2015春 惠州校级月考)如图,在铁 ( http: / / www.21cnjy.com )路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B. B点 C. C点 D. D点
10.(2015春 德州校级期中)如图,∠ACB=90°,CD⊥AB于D,则下面的结论中,正确的是( )
①AC与BC互相垂直②CD和BC互相垂直③点B到AC的垂线段是线段CA
④点C到AB的距离是线段CD⑤线段AC的长度是点A到BC的距离.
A.①⑤ B. ①④ C. ③⑤ D. ④⑤
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(10题图) (11题图) (12题图)
二.填空题(共10小题)
11.(2015春 泰山区期末)如图,直线AB,CD相交于点O,OE⊥AB,∠COE=68°,则∠BOD等于 .
12.(2015春 十堰期末)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.若∠EOD=35°,则∠AOC的度数为 °.
13.(2015春 周口期末)如图,直线A ( http: / / www.21cnjy.com )B、CD相交于O,OE⊥OF,OC平分∠AOE,且∠BOF=2∠BOE,则∠BOD= .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(13题图) (14题图) (15题图) (16题图)
14.(2015春 山西校 ( http: / / www.21cnjy.com )级期末)如图,要把池中的水引到D处,可过D点引DC⊥AB于C,然后沿DC开渠,可使所开渠道最短,试说明设计的依据: .
15.(2015春 娄底期末)如图,已 ( http: / / www.21cnjy.com )知,在直角三角形ABC中,∠A=90°,AB=3,AC=4,BC=5,则顶点A到BC边的距离等于 .
16.(2015春 北流市期中)如图,∠AOB=90°,∠MON=60°,OM平分∠AOB,ON平分∠BOC,则∠AOC= .
17.(2015春 北京校级期中) ( http: / / www.21cnjy.com )如图,直线AB,CD相交于O,OE⊥CD,OF⊥AB,∠DOF=65°,则∠BOE= ,∠AOC= .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(17题图) (18题图) (20题图)
18.(2015春 保定期末)如图 ( http: / / www.21cnjy.com ),立定跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离 4.6米.(填“大于”“小于”或“等于”)
19.(2015春 吉州区期末)在下列说法中 ( http: / / www.21cnjy.com ):①两点确定一条直线;②垂线段最短;③相等的角是对顶角;④三角形三条高、中线、角平分线都分别交于一点,正确的有 .(只填序号)
20.(2015春 揭西县校级月考)如图,PO⊥OR,OQ⊥PR,则点O到PR的所在的直线的距离是 的长.
三.解答题(共5小题)
21.(2015春 会宁县期中)如图,∠1=30°,AB⊥CD,垂足为O,EF经过点O.求∠2、∠3的度数.
( http: / / www.21cnjy.com )
22.(2015春 湖北校 ( http: / / www.21cnjy.com )级期中)如图,直线AB、CD相交于O点,∠AOC与∠AOD的度数比为4:5,OE⊥AB,OF平分∠DOB,求∠EOF的度数.
( http: / / www.21cnjy.com )
23.(2015春 淄博校级期中)如图所示,OA⊥OB,OC⊥OD,OE为∠BOD的平分线,∠BOE=17°.求∠AOC的度数.
( http: / / www.21cnjy.com )
24.(2015春 龙口市期中)如图:AB、CD、EF交于O点,AB⊥CD,OG平分∠AOE,∠COE=28°,求∠AOG的度数.
( http: / / www.21cnjy.com )
25.(2015春 连江 ( http: / / www.21cnjy.com )县期中)如图:直线AB,CD相交于点O,EO⊥AB,垂足为O,OF平分∠BOD,∠BOF=15°,求∠COE的度数.
( http: / / www.21cnjy.com )
青岛版七年级数学下册第8章8.5垂直同步训练题参考答案
一.选择题(共10小题)
1.B 2.B 3.C 4.C 5.B 6.C 7.B 8.C 9.A 10.A二.填空题(共10小题)
11.22° 12.55° 13.75° 14.垂线段最短 15.2.4 16.120°
17.65°25° 18.大于 19.①② 20.OQ
三.解答题(共5小题)
21.解:由题意得:
∠3=∠1=30°(对顶角相等)
∵AB⊥CD(已知)
∴∠BOD=90°(垂直的定义)
∴∠3+∠2=90°
即30°+∠2=90°
∴∠2=60°
22.解:设∠AOC=4x,则∠AOD=5x,
∵∠AOC+∠AOD=180°,∴4x+5x=180°,解得x=20°,
∴∠AOC=4x=80°,
∴∠BOD=80°,
∵OE⊥AB,∴∠BOE=90°,
∴∠DOE=∠BOE﹣∠BOD=10°,
又∵OF平分∠DOB,
∴∠DOF=∠BOD=40°,
∴∠EOF=∠EOD+∠DOF=10°+40°=50°.
23.解:∵OA⊥OB,OC⊥OD,∴∠AOB=∠COD=90°,
∵OE为∠BOD的平分线,∠BOE=17°,
∴∠BOD=2∠BOE=34°,
∴∠AOC=360°﹣90°﹣90°﹣34°=146°.
24.解:∵AB⊥CD,∴∠AOC=90°.
∵∠FOD与∠BOE是对顶角,∴∠COE=∠FOD=28°,
∴∠BOE=90°﹣∠COE=62°,
∴∠AOE=180°﹣62°=118°,
∵OG平分∠AOE,
∴∠AOG=∠AOE=×118°=59°.
25.解:∵OF平分∠BOD,∠BOF=15°,∴∠BOD=2∠BOF=30°,
∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=30°,
∵EO⊥AB,
∴∠AOC+∠COE=90°,
∴∠COE=90°﹣∠AOC=90°﹣30°=60°.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
