勾股定理(广东省汕头市金平区)
文档属性
| 名称 | 勾股定理(广东省汕头市金平区) |  | |
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-21 10:35:00 | ||
图片预览


文档简介
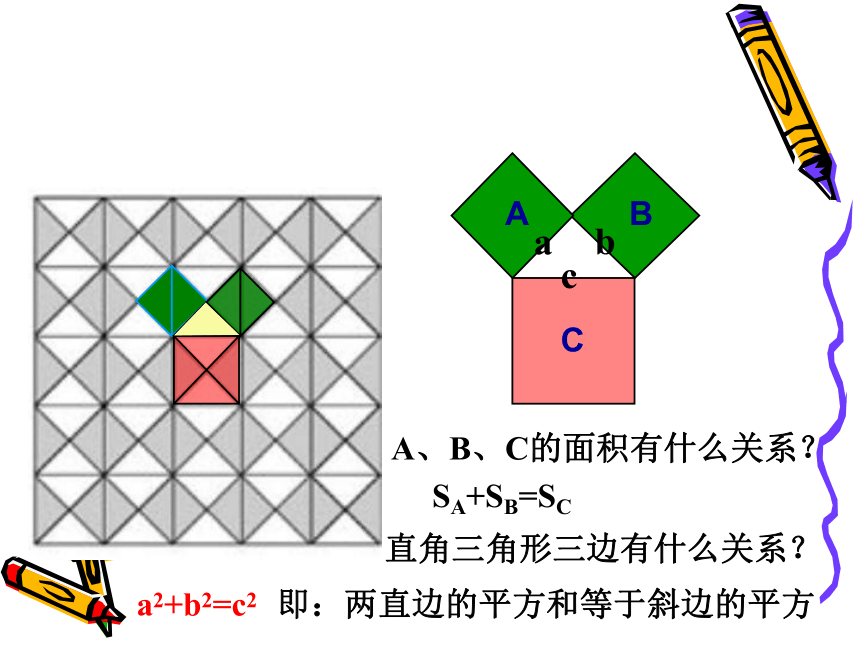
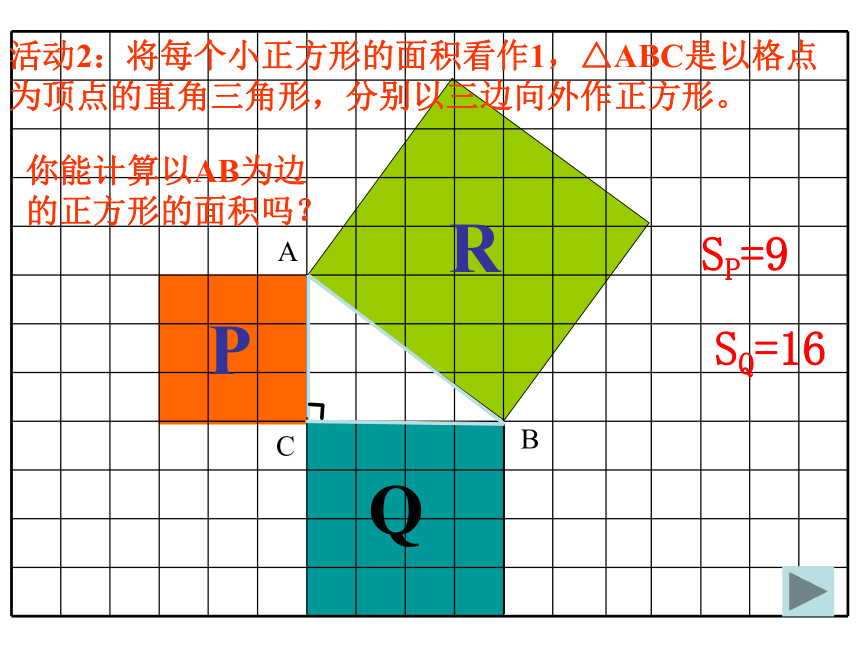
课件37张PPT。勾股定理3,4,55,12,13 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系. 我们也来观察右图中的地面,看看有什么发现?知识探究一A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SCa2+b2=c2即:两直边的平方和等于斜边的平方邮票赏析这是1955年希腊曾经发行的纪念一位数学家的邮票。观察这枚邮票图案小方格的个数,你有什么发现?知识探究二活动2:将每个小正方形的面积看作1,△ABC是以格点为顶点的直角三角形,分别以三边向外作正方形。ABCPQR你能计算以AB为边
的正方形的面积吗?SP=9
SQ=16
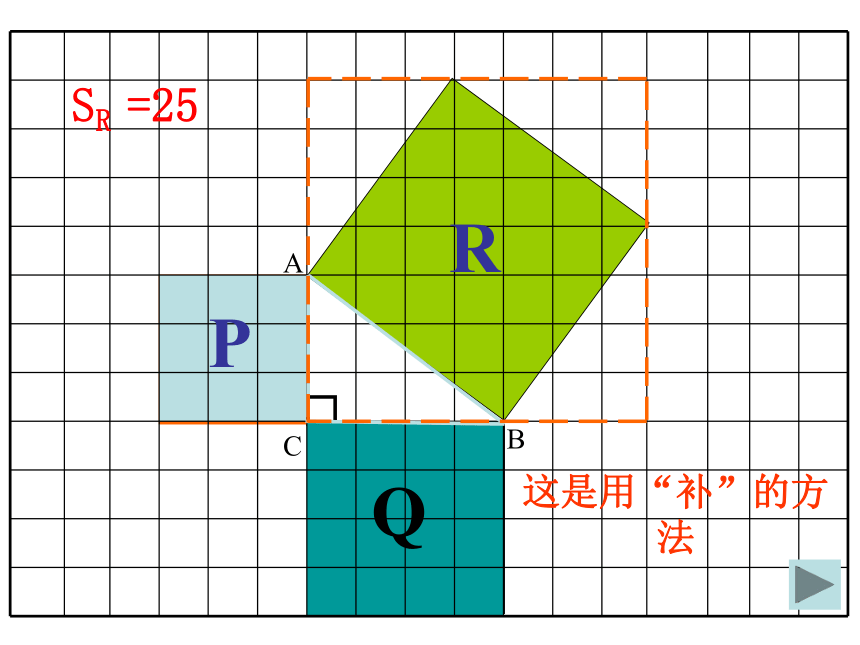
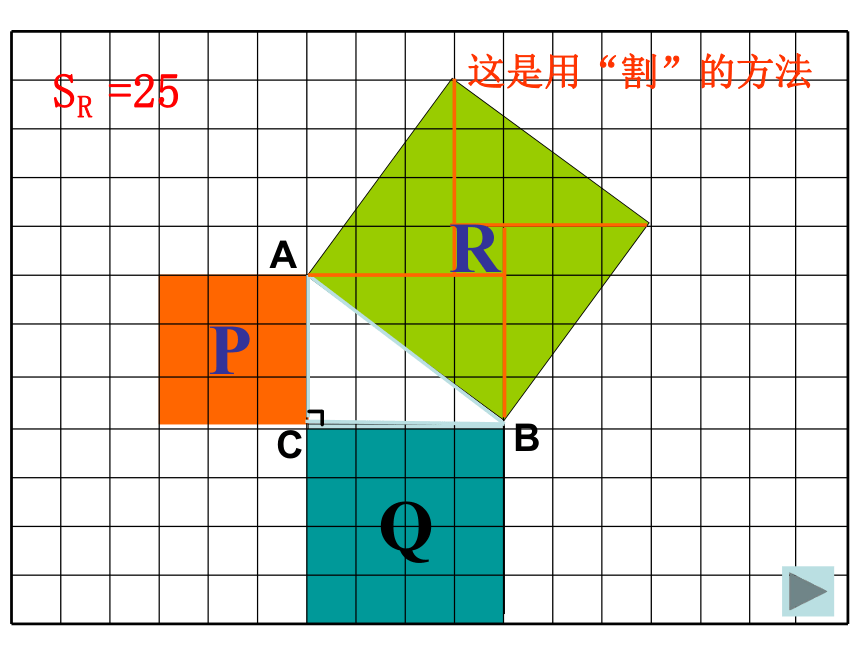
这是用“补”的方法ABCPQRSR =25
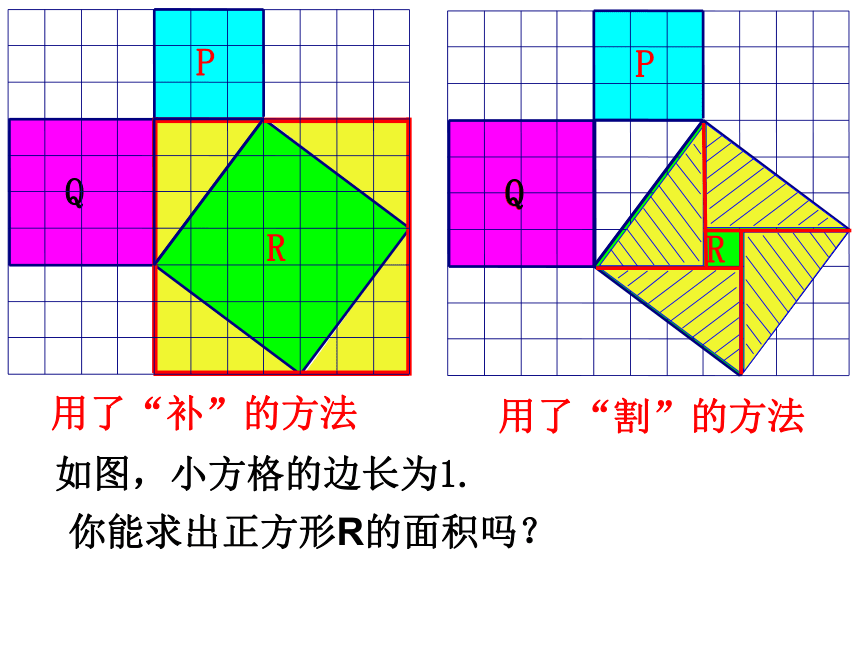
这是用“割”的方法PQRABCSR =25C如图,小方格的边长为1.(1)你能求出正方形R的面积吗?用了“补”的方法用了“割”的方法Q图2491392534SA+SB=SC两直角边的平方和
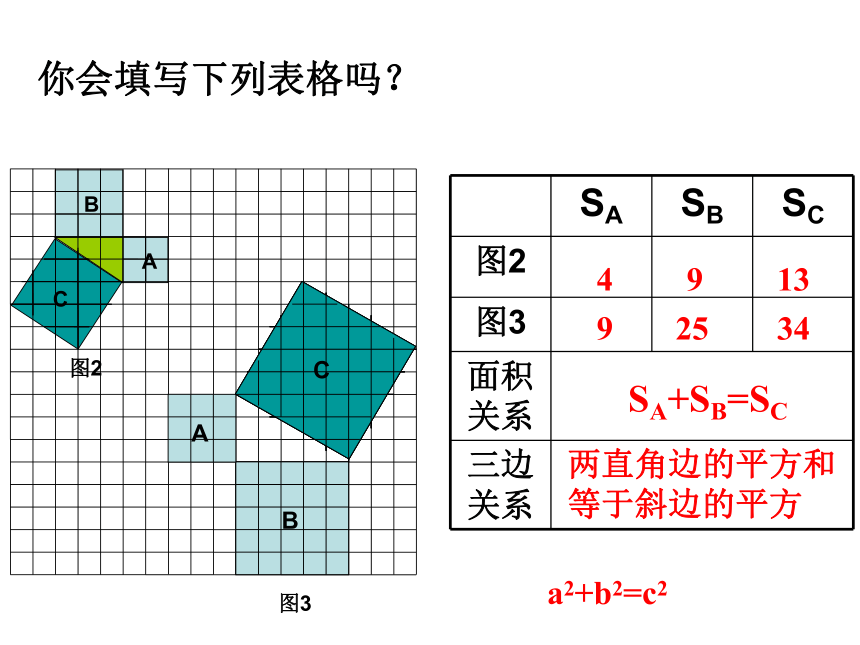
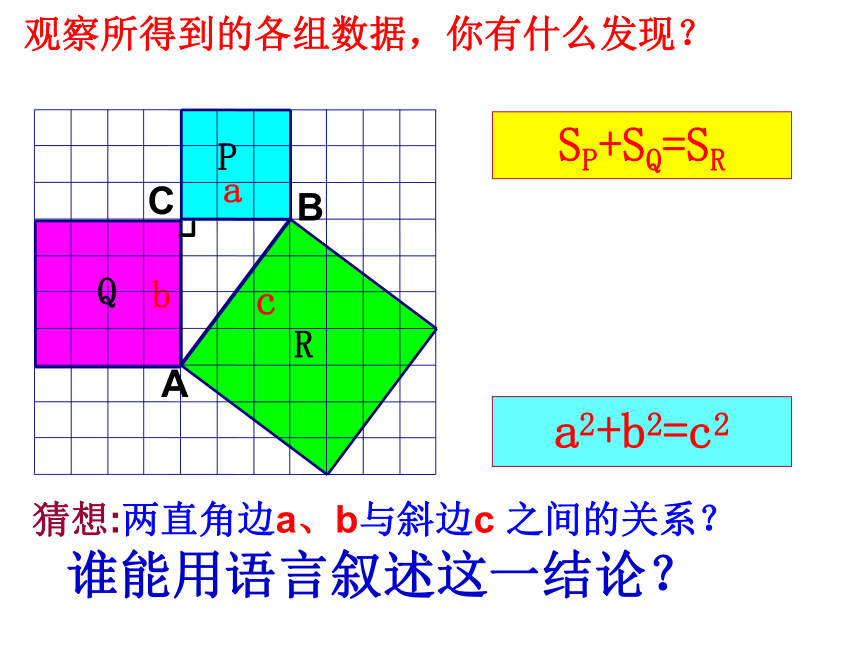
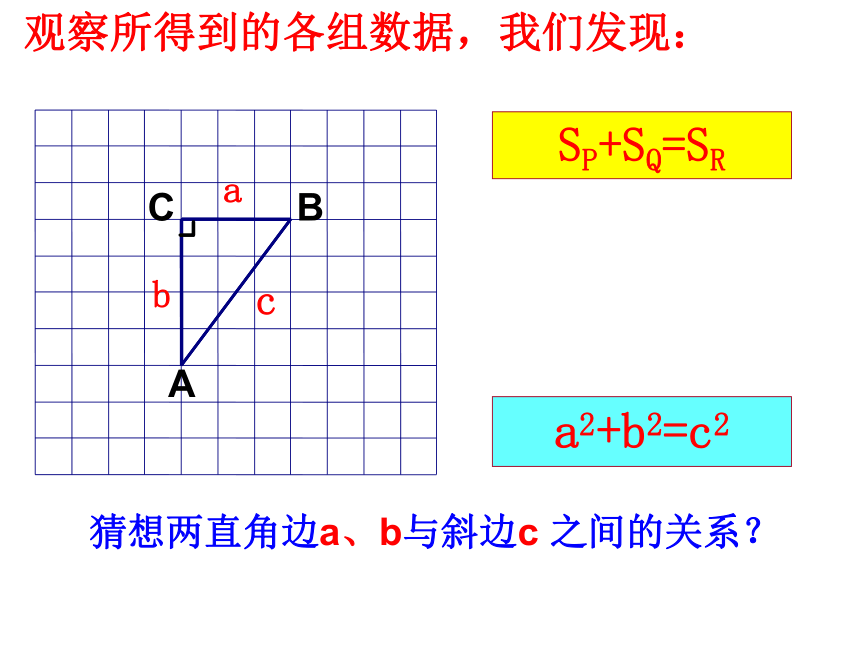
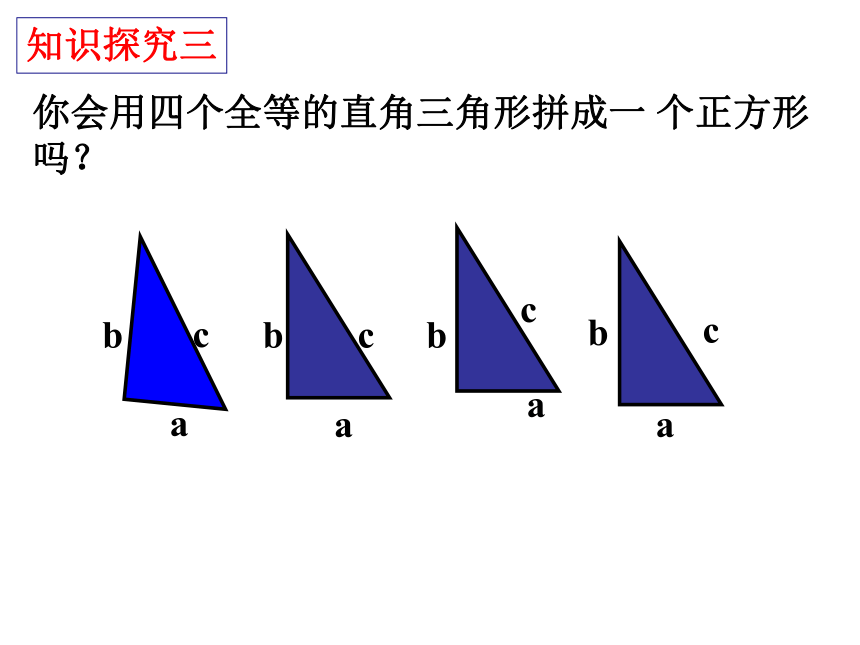
等于斜边的平方你会填写下列表格吗?a2+b2=c2acbSP+SQ=SR 观察所得到的各组数据,你有什么发现?猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2CAB谁能用语言叙述这一结论?acbSP+SQ=SR 观察所得到的各组数据,我们发现:猜想两直角边a、b与斜边c 之间的关系?a2+b2=c2CAB你会用四个全等的直角三角形拼成一 个正方形吗?abcabcabcabc知识探究三猜想的证明:cbacba定理:经过证明被确认为正确的命题叫做定理。勾股定理:如果直角三角形的两直角边长分别
为a、b,斜边为c,那么a2+b2=c2。 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。勾股定理的简单应用勾股定理应用的规范:(1)已知a、b,求c(2)已知a、 c ,求 b练一练:1、求下列字母所代表的正方形的面积。解:正方形A的面积
=225+400
=625 解:正方形B的面积
=81+225
=306 2、求出下列直角三角形中未知边的长度:∵x>0
∴x = 51.求下列图中表示边的未知数x、y、z的值.①81144xyz②③小试牛刀X=15Y=5Z=7比一比看看谁算得快!2.求下列直角三角形中未知边的长:8x171620x125x小试牛刀X=15X=12X=13①②③注意:像5、12、13这样,能构成直角三角形的三边的一组整数,我们称之为勾股数。1.常见的勾股数注意识记:3、4、5;5、12、13;8、15、17;7、24、25;9、40、412.常见的平方数112=121; 122=144; 132=169; 142=196;
152=225; 162=256; 172=289; 182=324;
192=361; 242=576; 252=625事实上,以上勾股数的整数倍也是勾股数。1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )A.3 米 B.4 米 C.5米 D.6米C34CBA2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=13千米,CB=12千米,则AB为 ( )A.5千米 B.12千米 C.10千米 D.13千米13 12 ?A3、如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?4、下列阴影部分是一个正方形,求此正方形的面积解:设正方形的边长为x厘米 , 则 x2=172-152
x2=64答:正方形的面积是64平方厘米。例:如图,将长为10米的梯子AC斜靠 在墙上,BC长为6米。
ABC106(1)求梯子上端A到墙的底端B的距离AB。(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?A1C1 2 25 已知:Rt△ABC中,AB=4,AC=3,则BC2的长为 . 或73、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?x+1BCAH12?┓xx2+22=(x+1)2盛开的水莲1046810xEFDCBA8-x8-xX2+42=(8-X)2 如图是 一大厦的柱子,它是圆柱形的 ,它的高是8米,底面半径是2米,一只壁虎在A点,想要吃到B点的昆虫,它爬行的最短距离 是多少?(圆周率取3)
82×3×26C102002年世界数学家大会会标本节课
你有什么收获?1. 课本70页,第4、7题;
2.查阅有关勾股定理的历史资料,
关注 验证勾股定理的方法. 请思考:如图,分别以直角三角形三边为直径作三个半圆
这三个半圆的面积之间有什么关系?为什么?
的正方形的面积吗?SP=9
SQ=16
这是用“补”的方法ABCPQRSR =25
这是用“割”的方法PQRABCSR =25C如图,小方格的边长为1.(1)你能求出正方形R的面积吗?用了“补”的方法用了“割”的方法Q图2491392534SA+SB=SC两直角边的平方和
等于斜边的平方你会填写下列表格吗?a2+b2=c2acbSP+SQ=SR 观察所得到的各组数据,你有什么发现?猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2CAB谁能用语言叙述这一结论?acbSP+SQ=SR 观察所得到的各组数据,我们发现:猜想两直角边a、b与斜边c 之间的关系?a2+b2=c2CAB你会用四个全等的直角三角形拼成一 个正方形吗?abcabcabcabc知识探究三猜想的证明:cbacba定理:经过证明被确认为正确的命题叫做定理。勾股定理:如果直角三角形的两直角边长分别
为a、b,斜边为c,那么a2+b2=c2。 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。勾股定理的简单应用勾股定理应用的规范:(1)已知a、b,求c(2)已知a、 c ,求 b练一练:1、求下列字母所代表的正方形的面积。解:正方形A的面积
=225+400
=625 解:正方形B的面积
=81+225
=306 2、求出下列直角三角形中未知边的长度:∵x>0
∴x = 51.求下列图中表示边的未知数x、y、z的值.①81144xyz②③小试牛刀X=15Y=5Z=7比一比看看谁算得快!2.求下列直角三角形中未知边的长:8x171620x125x小试牛刀X=15X=12X=13①②③注意:像5、12、13这样,能构成直角三角形的三边的一组整数,我们称之为勾股数。1.常见的勾股数注意识记:3、4、5;5、12、13;8、15、17;7、24、25;9、40、412.常见的平方数112=121; 122=144; 132=169; 142=196;
152=225; 162=256; 172=289; 182=324;
192=361; 242=576; 252=625事实上,以上勾股数的整数倍也是勾股数。1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )A.3 米 B.4 米 C.5米 D.6米C34CBA2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=13千米,CB=12千米,则AB为 ( )A.5千米 B.12千米 C.10千米 D.13千米13 12 ?A3、如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断之前有多高?4、下列阴影部分是一个正方形,求此正方形的面积解:设正方形的边长为x厘米 , 则 x2=172-152
x2=64答:正方形的面积是64平方厘米。例:如图,将长为10米的梯子AC斜靠 在墙上,BC长为6米。
ABC106(1)求梯子上端A到墙的底端B的距离AB。(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?A1C1 2 25 已知:Rt△ABC中,AB=4,AC=3,则BC2的长为 . 或73、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?x+1BCAH12?┓xx2+22=(x+1)2盛开的水莲1046810xEFDCBA8-x8-xX2+42=(8-X)2 如图是 一大厦的柱子,它是圆柱形的 ,它的高是8米,底面半径是2米,一只壁虎在A点,想要吃到B点的昆虫,它爬行的最短距离 是多少?(圆周率取3)
82×3×26C102002年世界数学家大会会标本节课
你有什么收获?1. 课本70页,第4、7题;
2.查阅有关勾股定理的历史资料,
关注 验证勾股定理的方法. 请思考:如图,分别以直角三角形三边为直径作三个半圆
这三个半圆的面积之间有什么关系?为什么?
