12.3.2 等边三角形(1)(广东省汕头市金平区)
文档属性
| 名称 | 12.3.2 等边三角形(1)(广东省汕头市金平区) |  | |
| 格式 | rar | ||
| 文件大小 | 385.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-22 12:58:00 | ||
图片预览





文档简介
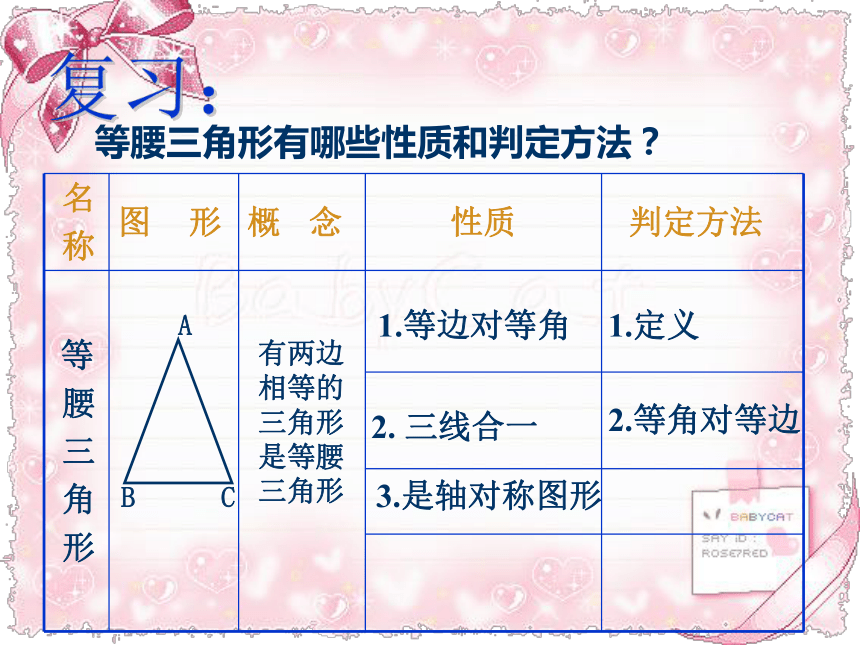
课件19张PPT。12.3.2 等边三角形(一)岐山二中 佘翠华等腰三角形有哪些性质和判定方法?有两边相等的三角形是等腰三角形1.等边对等角2. 三线合一3.是轴对称图形2.等角对等边1.定义复习:a>ba 三条边都相等的三角形叫做 等边三角形。等边三角形的三条边都相等等边三角形的三个内角都相等,并且每一个角都等于60 ° ABC等边三角形的性质:等边三角形是轴对称图形吗?如果是,
有几条对称轴?指出它的对称轴。
练习:
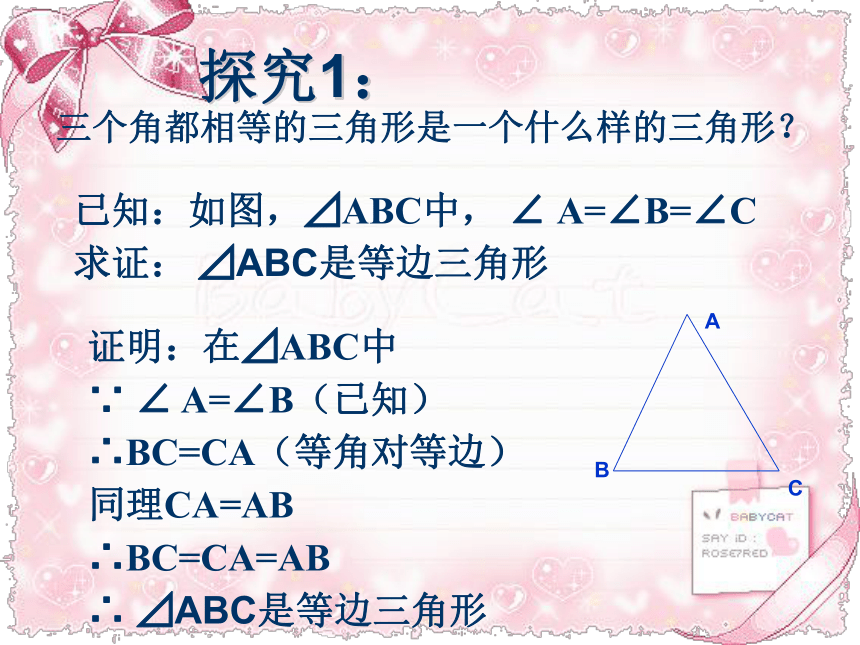
三个角都相等的三角形是一个什么样的三角形?已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证: ⊿ABC是等边三角形
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
∴ ⊿ABC是等边三角形探究1:三个角都相等的三角形是等边三角形。问题:如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?探究2
第二种情况:当底角是60°时。第一种情况:当顶角是60°时。已知: ⊿ABC中,AB=AC, ∠A=600。
求证: ⊿ABC是等边三角形证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴ ∠ A= ∠B=∠C
∴ ⊿ABC是等边三角形
已知: ⊿ABC中,AB=AC, ∠B=600。
求证:⊿ABC是等边三角形证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=600
∴ ∠C = 600
∴∠ A=600
∴∠ A= ∠B=∠C
∴ ⊿ABC是等边三角形
有一个角是60°的等腰三角形是等边三角形。等边三角形的判定方法1.三边相等的三角形是等边三角形.(定义)
2.三个角都相等的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
归纳:应用举例:例.如图, △ABC是等边三角形,DE//BC,
交AB,AC于D,E
求证:△ADE是等边三角形本题还有其他证明方法吗?证明: ∵ △ ABC是等边三角形
∴ ∠ A=∠B=∠C
∵ DE//BC
∴ ∠ADE = ∠B, ∠AED = ∠C
∴∠ A= ∠ADE = ∠AED
∴ △ ADE是等边三角形
巩固练习:2. 如图,等边三角形ABC 中, AD是 BC上
的高, ∠BDE = ∠CDF= 60 °,图中有
哪些与BD相等的线段?
∴与BD相等的线段有
CD,CF,BE,DE,
FD,AF,AE课堂小结: 这节课我们主要学习了哪些内容?有哪些收获?2.三个角都是60°4.是轴对称图形,对称轴有三条。2.三个角都相等的三角形1.定义3.有一个内角等于 60°的等腰三角形三条边都相等的三角形是等边三角形1.三边相等3.三线合一课外探究:
等边三角形三条中线相交于一点,画出图形,找出图中所有的全等三角形。
作业布置:
课本P58,习题12.3,第11题再见!!!练一练
如图,在等边⊿ABC中,D、E分别是BC、
AC上的点,且BD=CE,BE交AD于P,
求证:(1)⊿ADC≌⊿BEA
(2) ∠APE= 60 °
课外补充题1.已知:D,E是△ABC中BC上的两点,
且BD=DE=EC=AD=AE.
求∠ B与∠ BAC的度数.
2.已知:△ABC是等边三角形,D,E,F分别
是各边上的一点,且AD=BE=CF.
试说明△ DEF是等边三角形.
有几条对称轴?指出它的对称轴。
练习:
三个角都相等的三角形是一个什么样的三角形?已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证: ⊿ABC是等边三角形
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
∴ ⊿ABC是等边三角形探究1:三个角都相等的三角形是等边三角形。问题:如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?探究2
第二种情况:当底角是60°时。第一种情况:当顶角是60°时。已知: ⊿ABC中,AB=AC, ∠A=600。
求证: ⊿ABC是等边三角形证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴ ∠ A= ∠B=∠C
∴ ⊿ABC是等边三角形
已知: ⊿ABC中,AB=AC, ∠B=600。
求证:⊿ABC是等边三角形证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=600
∴ ∠C = 600
∴∠ A=600
∴∠ A= ∠B=∠C
∴ ⊿ABC是等边三角形
有一个角是60°的等腰三角形是等边三角形。等边三角形的判定方法1.三边相等的三角形是等边三角形.(定义)
2.三个角都相等的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
归纳:应用举例:例.如图, △ABC是等边三角形,DE//BC,
交AB,AC于D,E
求证:△ADE是等边三角形本题还有其他证明方法吗?证明: ∵ △ ABC是等边三角形
∴ ∠ A=∠B=∠C
∵ DE//BC
∴ ∠ADE = ∠B, ∠AED = ∠C
∴∠ A= ∠ADE = ∠AED
∴ △ ADE是等边三角形
巩固练习:2. 如图,等边三角形ABC 中, AD是 BC上
的高, ∠BDE = ∠CDF= 60 °,图中有
哪些与BD相等的线段?
∴与BD相等的线段有
CD,CF,BE,DE,
FD,AF,AE课堂小结: 这节课我们主要学习了哪些内容?有哪些收获?2.三个角都是60°4.是轴对称图形,对称轴有三条。2.三个角都相等的三角形1.定义3.有一个内角等于 60°的等腰三角形三条边都相等的三角形是等边三角形1.三边相等3.三线合一课外探究:
等边三角形三条中线相交于一点,画出图形,找出图中所有的全等三角形。
作业布置:
课本P58,习题12.3,第11题再见!!!练一练
如图,在等边⊿ABC中,D、E分别是BC、
AC上的点,且BD=CE,BE交AD于P,
求证:(1)⊿ADC≌⊿BEA
(2) ∠APE= 60 °
课外补充题1.已知:D,E是△ABC中BC上的两点,
且BD=DE=EC=AD=AE.
求∠ B与∠ BAC的度数.
2.已知:△ABC是等边三角形,D,E,F分别
是各边上的一点,且AD=BE=CF.
试说明△ DEF是等边三角形.
