3.2分数乘法(二)(讲义)-2023-2024学年五年级下册数学(北师大版)(含解析)
文档属性
| 名称 | 3.2分数乘法(二)(讲义)-2023-2024学年五年级下册数学(北师大版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 235.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 14:34:00 | ||
图片预览




文档简介
3.2分数乘法(二)(知识精讲+典题精练)
2023-2024学年五年级下册数学重难点同步培优讲义
(北师大版)
1.分数乘法
【知识点归纳】
分数乘法的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算.
乘积是1的两个数叫做互为倒数.
分数乘法法则:
(1)分数乘以整数或整数乘以分数:由于任何整数(0除外)都可以化成分母是1的假分数,分数乘以整数或整数乘以分数,都可以转化成分数乘以分数的形式.因此,在计算中,是用分数的分子和整数相乘的积作为分子,分母不变.在乘的过程中,如果有可以约分的数,可以先约分,这样,可以使计算的数字缩小,从而使计算变得简便.
(2)分数乘以分数:用分子相乘的积作为分子,用分母相乘的积作为分母.为了使计算简便,在计算的过程中,能够约分的,要约分.
(3)带分数乘法:先把带分数化成假分数,然后再乘.结果是假分数时,要把假分数化成带分数或整数.
分数乘法的运算定律:
(1)交换律:两个分数相乘,交换分数的位置,它们的积不变.
(2)结合律:三个分数相乘,先把前两个分数相乘,再乘以第三个分数,或者先把后两个分数相乘,再乘以第一个分数,它们的积不变.
(3)乘法分配律:两个分数的和与一个分数相乘所得的积,等于每一个加数分别与这个分数相乘所得的积的和.
2.整数乘分数
【知识点归纳】
1、一个数乘分数的意义就是求一个数的几分之几是多少。
2、“一个数乘分数”指的是第二个因数必须是分数,不能是整数。(第一个因数是什么都可以)
【方法总结】
①整数与分数相乘,用分数的分子与整数相乘,分母不变;
②计算时能约分的可以先约分再计算出结果。
一.选择题(共6小题)
1.(如图)下列算式最符合图意的是( )
A. B. C.
2.下面图形不能正确表示×气的是( )
A.
B.
C.
D.
3.下面( )组中两个数的积在和之间。
A. B. C.
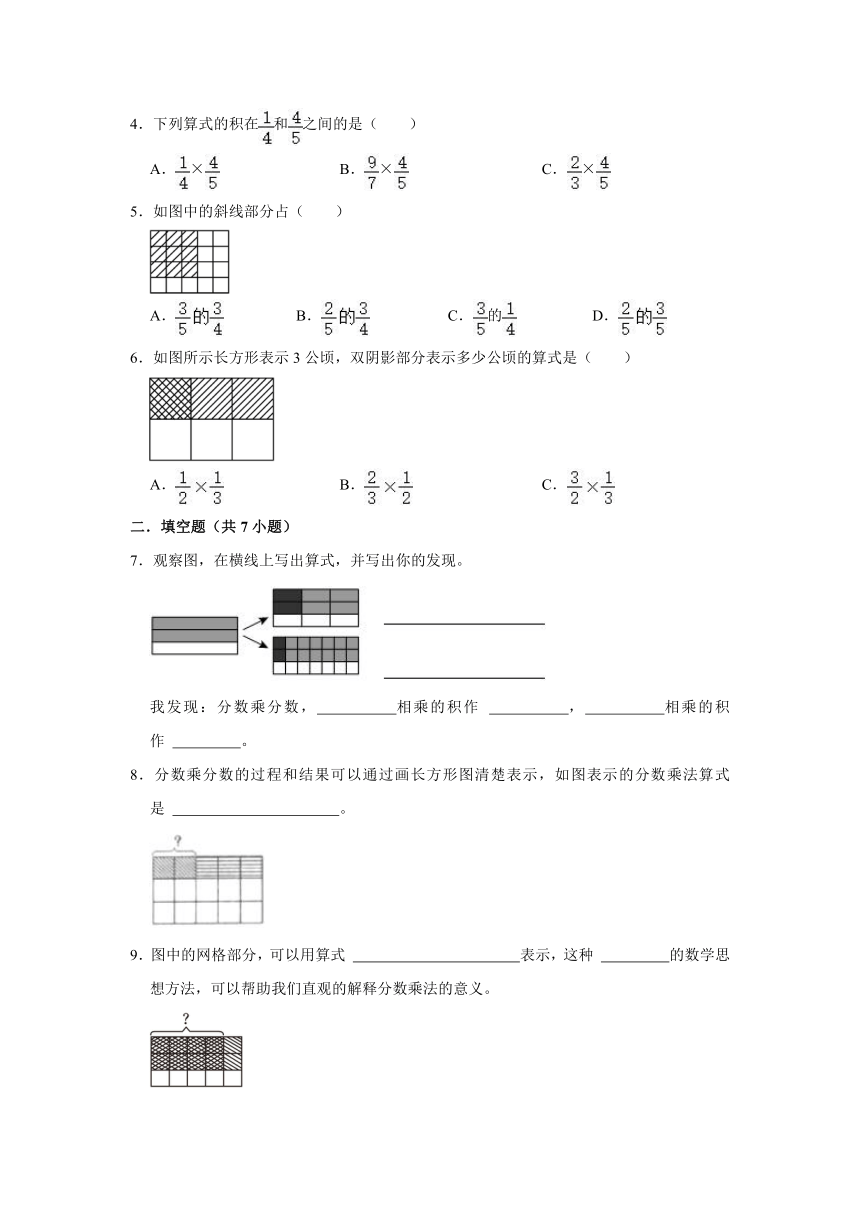
4.下列算式的积在和之间的是( )
A.× B.× C.×
5.如图中的斜线部分占( )
A. B. C.的 D.
6.如图所示长方形表示3公顷,双阴影部分表示多少公顷的算式是( )
A. B. C.
二.填空题(共7小题)
7.观察图,在横线上写出算式,并写出你的发现。
我发现:分数乘分数, 相乘的积作 , 相乘的积作 。
8.分数乘分数的过程和结果可以通过画长方形图清楚表示,如图表示的分数乘法算式是 。
9.图中的网格部分,可以用算式 表示,这种 的数学思想方法,可以帮助我们直观的解释分数乘法的意义。
10.甲是乙的,乙是丙的,甲是36 。
11. =2 = ×0.6=2.5× =1
12.40千克增加后是 千克,40千克增加千克后是 千克,40千克比 千克少。
13.表示把 看作单位“1”的量,平均分成 份,取其中的 ,即求 的 是多少.
三.判断题(共8小题)
14.比80千克多是千克。
15.分数乘分数,积一定小于每一个因数. .
16.分数乘分数,用分子相加的和作分子,用分母相加的和作分母。
17.2吨煤烧去后,还剩吨.
18.60分米的和40分米的长度相等。
19.50米比40米长。
20.分数乘分数的方法适用于分数乘整数。
21.两个数相乘,积一定大于其中的任何一个因数.
四.计算题(共1小题)
22.直接写得数。
= = = 1﹣=
0.2﹣= = = =
= ()×12=
五.应用题(共6小题)
23.在下面长方形中画图表示算式×,并计算出结果是多少.
24.甲数是乙数的,丙数是甲数的,那么丙数是乙数的几分之几?
25.杭州亚运会9月8日启动火炬传递,整个传递过程有2022名火炬手参加,其中年龄最大的火炬手今年84岁,最小火炬手今年多少岁?
26.红星小学开展了社团活动课,航模小组和美术小组一共有45人,美术小组的人数是航模小组的
27.一瓶果汁的净含量是升,4瓶这样的果汁一共是多少升?小华喝了这瓶果汁的,喝了多少升?
28.从北京飞往广州的时间大约是4小时,飞往拉萨用的时间是飞往广州所用时间的2倍,飞往西安所用的时间是飞往拉萨所用时间的
3.2分数乘法(二)(知识精讲+典题精练)-2023-2024学年五年级下册(北师大版)
参考答案与试题解析
一.选择题(共6小题)
1.【答案】C
【分析】先将大长方形平均分成4份,取其中的3份;再将这3份平均分成3份,取其中的1份。据此解答。
【解答】解:
×=
故选:C。
【点评】本题考查了结合图示进行分数乘分数的运算,突出了对算理的理解。
2.【答案】D
【分析】算式×表示先把单位“1”平均分成4份,取其中的3份;再把这3份平均分成3份,取其中的2份。据此解答。
【解答】解:选项A,将一条线段看作单位“1”,取其中的3份,取其中的5份;
选项B,把12个长方形看作单位“1”,取其中的3份,取其中的6份;
选项C,把8个圆看作单位“1”,取其中的7份,取其中的2份;
选项D,把大长方形看作单位“1”,取其中的2份,取其中的2份。
故选:D。
【点评】本题考查了分数乘分数,突出了对算理的理解。
3.【答案】A
【分析】首先根据分数乘法的计算法则,分别计算出各式的结果,然后再根据分数大小比较的方法进行比较即可。
【解答】解:×=
×=
×=
大于,所以不符合题意;
小于,所以不符合题意;
只有在和之间。
故选:A。
【点评】此题考查的目的是理解掌握分数乘法的计算法则以及分数大小比较的方法。
4.【答案】C
【分析】现将上面的算式计算出积,然后与和进行比较即可。
【解答】解:×=;<,所以A不在和;
×=;>,所以B不在和;
×=,>>,所以C在和。
则上面算式的积在和之间的是C。
故选:C。
【点评】此题考查了分数大小的比较,要求学生掌握。
5.【答案】A
【分析】把长方形平均分成5份,涂色部分占3份,把涂色部分平均分成4份,取其中的3份。
【解答】解:斜线部分占的。
故选:A。
【点评】本题考查的主要内容是分数乘法的应用问题。
6.【答案】C
【分析】观察图可知:先把长方形平均分成了2份,其中的1份就是它的,3公顷的就是公顷,再把这1份平均分成3份,其中的1份就是公顷的,由此求解。
【解答】解:
整个阴影部分表示3公顷的,也就是,双阴影部分表示,即:×。
故选:C。
【点评】解决本题要注意题目要求的是多少公顷,而不是整个图形的几分之几,要结合分数的意义和分数乘法的意义求解。
二.填空题(共7小题)
7.【答案】;分子,分子,分母,分母。
【分析】依据题意结合图示可知,把大长方形的面积看作单位“1”,涂色部分占单位“1”的,把涂色部分的面积看作单位“1”,第二次涂色部分分别占涂色部分的几分之几,由此解答本题。
【解答】解:
我发现:分数乘分数,分子相乘的积作分子。
故答案为:分子,分子,分母。
【点评】本题考查的是分数乘法的意义的应用。
8.【答案】×。
【分析】通过图形看结果“?”处表示,从结果看,就是把单位“1”分成15份,并找出这个长方形的,即长方形中最上方的部分,在再把这个图形分成5份,找出其中的2份,据此解答。
【解答】解:把长方形平分成3份,找到其中的一份,即,然后把这个,再找到这3份其中2份,用,则这个2份占整个长方形的×=。
故答案为:×。
【点评】本题主要考查分数乘分数的结果在长方形中的推导过程。
9.【答案】×,转化。
【分析】根据图示可知,是把长方形平均分成3份,涂色其中的2份用分数表示;再把涂色的长方形平均分成5份,再涂色其中的4份就用分数表示,两次涂色的部分占长方形的几分之几就是求一个分数的几分之几是多少,用乘法计算,利用转化的思想直观的解释分数乘法的意义。
【解答】解:图中的网格部分,可以用算式×,这种转化的数学思想方法。
故答案为:×,转化。
【点评】本题考查了分数乘法的意义。
10.【答案】72。
【分析】由“甲是乙的”可知,单位“1”是乙,由“乙是丙的”可知,单位“1”是“丙”据此根据单位“1”的量=对应量÷对应分率,代入数值求出乙的值,进而求出丙的值,据此解答。
【解答】解:36=54
54=72
答:丙是72。
故答案为:72。
【点评】解答此题的关键是分清两个单位“1”的区别,求单位“1”的几分之几用乘法计算;已知单位“1”的几分之几是多少,求单位“1”用除法计算。
11.【答案】;;;0.4。
【分析】根据一个因数=积÷另一个因数,用1分别除以已知因数即可。
【解答】解:1÷=
3÷2=
2÷0.6=
1÷2.5=0.4
所以,=2=。
故答案为:;;;3.4。
【点评】考查了乘法各部分名称之间的关系的运用。
12.【答案】48;40;50。
【分析】求40千克增加后是多少千克,就是求40乘(1+)的积;求40千克增加千克后是多少千克,就是求40与的和;求40千克比多少千克少,就是求40除以(1﹣)的商。
【解答】解:40×(1+)
=40×
=48(千克)
40+=40
40÷(1﹣)
=40÷
=50(千克)
答:40千克增加后是48千克千克后是40,40千克比50千克少。
故答案为:48;40。
【点评】求比一个数多几分之几的数是多少,用乘法计算;已知比一个数少几分之几的数是多少,用除法计算。
13.【答案】见试题解答内容
【分析】35×表示把35看作单位“1”,平均分成7份,去其中的3份是多少,即求35的是多少.
【解答】解:35×表示把35看作单位“4”,去其中的3份是多少是多少.
故答案为:35,7,3,35,.
【点评】此题属于求一个数的几分之几是多少,解答关键是确定单位“1”,根据一个数乘分数的意义,用乘法解答.
三.判断题(共8小题)
14.【答案】×
【分析】要求比80千克多是多少千克,先用80乘求出多的质量,然后再加上80千克即可。
【解答】解:80×+80
=60+80
=140(千克)
答:比80千克多是140千克。
所以原题说法错误。
故答案为:×。
【点评】求比一个数多几分之几的数是多少,用乘法进行解答。
15.【答案】见试题解答内容
【分析】如果两个分数都大于1,它们的积就比两个分数大,可以通过举例证明.
【解答】解:两个分数相乘的积不一定小于每一个因数,例如:.
因此,分数乘分数,这种说法是错误的.
故答案为:×.
【点评】此题可用举例法进行解答.
16.【答案】×
【分析】分数乘分数:分子的乘积作分子,分母的乘积作分母,能约分的可以先约分,由此判断即可。
【解答】解:分数乘分数:分子的乘积作分子,分母的乘积作分母。
故答案为:×。
【点评】本题考查了分数乘分数的计算法则,要熟练掌握,灵活运算。
17.【答案】×
【分析】把2吨看作单位“1”,用去后,剩下的占原来的(1),根据一个数乘分数的意义,求出剩下的吨数与吨进行比较即可.
【解答】解:2×
=
=1(吨),
答:还剩1吨.
故答案为:×.
【点评】此题解答关键是确定单位“1”,求出剩下的占原来的几分之几,再根据一个数乘分数的意义,用乘法解答.
18.【答案】√
【分析】求一个数的几分之几是多少,用乘法计算,据此分别用60乘、40乘计算出60分米的和40分米的的长度,再进行比较。
【解答】解:60×=24(分米)
40×=24(分米)
答:60分米的和40分米的。
原题说法正确。
故答案为:√。
【点评】求一个数的几分之几是多少,用乘法计算。
19.【答案】√
【分析】先利用减法求出50米比40米多多少米,再利用多的数量÷40米,即可解答。
【解答】解:50﹣40=10(米)
10÷40=
因此50米比40米多,原题说法正确。
故答案为:√。
【点评】求一个数比另一个数多几分之几,用多出的数量除以单位“1”的数量。
20.【答案】√
【分析】根据分数乘法的计算法则,由于任何整数(0除外)都可以化成分母是1的假分数,分数乘整数或整数乘分数,都可以转化成分数乘以分数的形式,因此,在计算中,是用分数的分子和整数相乘的积作为分子,分母不变.在乘的过程中,如果有可以约分的数,可以先约分;分数乘以分数:用分子相乘的积作为分子,用分母相乘的积作为分母.为了使计算简便,在计算的过程中,能够约分的,要约分,判读即可。
【解答】解:根据由于任何整数(0除外)都可以化成分母是1的假分数,分数乘整数或整数乘分数,因此,是用分数的分子和整数相乘的积作为分子;在乘的过程中,可以先约分,用分母相乘的积作为分母,在计算的过程中,要约分。原题说法正确。
故答案为:√。
【点评】此题重点考查了分数乘法计算法则的掌握情况。
21.【答案】×
【分析】此题根据两个因数都大于1,或都小于1,以及它们的积,来加以判断.可以举出例子说明.
【解答】解:如果两个因数都大于1,积一定大于其中的任何一个因数;
如果两个因数小于1,积一定小于其中的任何一个因数;
例如8.1×0.2=0.002,积小于0.4和0.2.
故答案为:×.
【点评】此题考查了因数与积的关系,对于这样的问题,一般举出反例加以说明.
四.计算题(共1小题)
22.【答案】;;;;0;1;;;0;7。
【分析】异分母分数相加减,要先通分,化成同分母分数后再计算。
分数乘法的计算法则,分子相乘的积做分子,分母相乘的积做分母。
【解答】解:
= = = 1﹣=
0.2﹣=0 =1 = =
=0 ()×12=5
【点评】本题解题关键是熟练掌握异分母分数加减法和分数乘法的计算方法。
五.应用题(共6小题)
23.【答案】见试题解答内容
【分析】分数乘分数表示求一个分数的几分之几是多少,表示求的是多少,画图表示这个算式分两步,第一步,将长方形看作单位”1“,平均分成两份,涂其中的一份,表示它的;第二步,把涂色部分看作单位”1“,平均分成5份,涂其中的3份,表示的.
【解答】解:如图:
【点评】分数既可以表示具体的数,也可以表示两个量之间的关系,当表示关系时一定要分辨清谁是单位”1“.
24.【答案】。
【分析】根据题意,把乙数看作单位“1”,甲数是乙数的,丙数是甲数的,可以分别求出甲数和乙数,再根据求一个数是另一个数的几分之几用除法,即可解答。
【解答】解:把乙数看作单位“1”,甲数是乙数的
所以甲数:7×
丙数:=
答:丙数是乙数的。
【点评】熟练掌握求一个数是另一个数的几分之几用除法是解题的关键。
25.【答案】14岁。
【分析】把最大火炬手年龄看作单位“1”,年龄最小的火炬手是最大火炬手年龄的,用乘法计算,即可得最小火炬手今年多少岁。
【解答】解:84×=14(岁)
答:最小火炬手今年14岁。
【点评】本题主要考查了分数乘法应用题,已知一个数,求它的几分之几是多少,用乘法计算。
26.【答案】25人,20人。
【分析】航模小组和美术小组一共有45人,美术小组的人数是航模小组的,根据分数加法的意义,全部人数是航模小组人数的(1+),根据分数除法的意义,用总人数除以其占航模小组人数的分率,即得航模小组多少人,然后用减法求出美术小组人数。
【解答】解:45÷(1+)
=45×
=25(人)
45﹣25=20(人)
答:航模小组有25人,美术小组有20人。
【点评】首先根据已知条件求出总人数是航模小组人数的几分之几,进而求出航模小组人数是完成本题的关键。
27.【答案】见试题解答内容
【分析】一瓶果汁的净含量是升,求4瓶这样的果汁一共是多少升,用乘法计算;小华喝了这瓶果汁的,就是求的是多少,用乘法计算.
【解答】解:×4=3(升)
×=(升)
答:4瓶这样的果汁一共是5升,小华喝了这瓶果汁的升.
【点评】本题考查了分数乘法的意义:
1,分数乘整数:和整数乘法意义相同,就是求几个相同加数和的简便运算;
2,一个数乘分数:是求这个数的几分之几是多少.
28.【答案】2小时。
【分析】根据整数乘法的意义,北京飞往广州的时间乘2等于北京飞往拉萨的时间,根据分数乘法的意义,用飞往拉萨用的时间乘就是从北京飞往西安的时间。
【解答】解:4×2×
=8×
=2(小时)
答:从北京飞往西安大约用了5小时。
【点评】求一个数的几倍是多少,用这个数乘倍数;求一个数的几分之几是多少,用这个数乘分率。
2023-2024学年五年级下册数学重难点同步培优讲义
(北师大版)
1.分数乘法
【知识点归纳】
分数乘法的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算.
乘积是1的两个数叫做互为倒数.
分数乘法法则:
(1)分数乘以整数或整数乘以分数:由于任何整数(0除外)都可以化成分母是1的假分数,分数乘以整数或整数乘以分数,都可以转化成分数乘以分数的形式.因此,在计算中,是用分数的分子和整数相乘的积作为分子,分母不变.在乘的过程中,如果有可以约分的数,可以先约分,这样,可以使计算的数字缩小,从而使计算变得简便.
(2)分数乘以分数:用分子相乘的积作为分子,用分母相乘的积作为分母.为了使计算简便,在计算的过程中,能够约分的,要约分.
(3)带分数乘法:先把带分数化成假分数,然后再乘.结果是假分数时,要把假分数化成带分数或整数.
分数乘法的运算定律:
(1)交换律:两个分数相乘,交换分数的位置,它们的积不变.
(2)结合律:三个分数相乘,先把前两个分数相乘,再乘以第三个分数,或者先把后两个分数相乘,再乘以第一个分数,它们的积不变.
(3)乘法分配律:两个分数的和与一个分数相乘所得的积,等于每一个加数分别与这个分数相乘所得的积的和.
2.整数乘分数
【知识点归纳】
1、一个数乘分数的意义就是求一个数的几分之几是多少。
2、“一个数乘分数”指的是第二个因数必须是分数,不能是整数。(第一个因数是什么都可以)
【方法总结】
①整数与分数相乘,用分数的分子与整数相乘,分母不变;
②计算时能约分的可以先约分再计算出结果。
一.选择题(共6小题)
1.(如图)下列算式最符合图意的是( )
A. B. C.
2.下面图形不能正确表示×气的是( )
A.
B.
C.
D.
3.下面( )组中两个数的积在和之间。
A. B. C.
4.下列算式的积在和之间的是( )
A.× B.× C.×
5.如图中的斜线部分占( )
A. B. C.的 D.
6.如图所示长方形表示3公顷,双阴影部分表示多少公顷的算式是( )
A. B. C.
二.填空题(共7小题)
7.观察图,在横线上写出算式,并写出你的发现。
我发现:分数乘分数, 相乘的积作 , 相乘的积作 。
8.分数乘分数的过程和结果可以通过画长方形图清楚表示,如图表示的分数乘法算式是 。
9.图中的网格部分,可以用算式 表示,这种 的数学思想方法,可以帮助我们直观的解释分数乘法的意义。
10.甲是乙的,乙是丙的,甲是36 。
11. =2 = ×0.6=2.5× =1
12.40千克增加后是 千克,40千克增加千克后是 千克,40千克比 千克少。
13.表示把 看作单位“1”的量,平均分成 份,取其中的 ,即求 的 是多少.
三.判断题(共8小题)
14.比80千克多是千克。
15.分数乘分数,积一定小于每一个因数. .
16.分数乘分数,用分子相加的和作分子,用分母相加的和作分母。
17.2吨煤烧去后,还剩吨.
18.60分米的和40分米的长度相等。
19.50米比40米长。
20.分数乘分数的方法适用于分数乘整数。
21.两个数相乘,积一定大于其中的任何一个因数.
四.计算题(共1小题)
22.直接写得数。
= = = 1﹣=
0.2﹣= = = =
= ()×12=
五.应用题(共6小题)
23.在下面长方形中画图表示算式×,并计算出结果是多少.
24.甲数是乙数的,丙数是甲数的,那么丙数是乙数的几分之几?
25.杭州亚运会9月8日启动火炬传递,整个传递过程有2022名火炬手参加,其中年龄最大的火炬手今年84岁,最小火炬手今年多少岁?
26.红星小学开展了社团活动课,航模小组和美术小组一共有45人,美术小组的人数是航模小组的
27.一瓶果汁的净含量是升,4瓶这样的果汁一共是多少升?小华喝了这瓶果汁的,喝了多少升?
28.从北京飞往广州的时间大约是4小时,飞往拉萨用的时间是飞往广州所用时间的2倍,飞往西安所用的时间是飞往拉萨所用时间的
3.2分数乘法(二)(知识精讲+典题精练)-2023-2024学年五年级下册(北师大版)
参考答案与试题解析
一.选择题(共6小题)
1.【答案】C
【分析】先将大长方形平均分成4份,取其中的3份;再将这3份平均分成3份,取其中的1份。据此解答。
【解答】解:
×=
故选:C。
【点评】本题考查了结合图示进行分数乘分数的运算,突出了对算理的理解。
2.【答案】D
【分析】算式×表示先把单位“1”平均分成4份,取其中的3份;再把这3份平均分成3份,取其中的2份。据此解答。
【解答】解:选项A,将一条线段看作单位“1”,取其中的3份,取其中的5份;
选项B,把12个长方形看作单位“1”,取其中的3份,取其中的6份;
选项C,把8个圆看作单位“1”,取其中的7份,取其中的2份;
选项D,把大长方形看作单位“1”,取其中的2份,取其中的2份。
故选:D。
【点评】本题考查了分数乘分数,突出了对算理的理解。
3.【答案】A
【分析】首先根据分数乘法的计算法则,分别计算出各式的结果,然后再根据分数大小比较的方法进行比较即可。
【解答】解:×=
×=
×=
大于,所以不符合题意;
小于,所以不符合题意;
只有在和之间。
故选:A。
【点评】此题考查的目的是理解掌握分数乘法的计算法则以及分数大小比较的方法。
4.【答案】C
【分析】现将上面的算式计算出积,然后与和进行比较即可。
【解答】解:×=;<,所以A不在和;
×=;>,所以B不在和;
×=,>>,所以C在和。
则上面算式的积在和之间的是C。
故选:C。
【点评】此题考查了分数大小的比较,要求学生掌握。
5.【答案】A
【分析】把长方形平均分成5份,涂色部分占3份,把涂色部分平均分成4份,取其中的3份。
【解答】解:斜线部分占的。
故选:A。
【点评】本题考查的主要内容是分数乘法的应用问题。
6.【答案】C
【分析】观察图可知:先把长方形平均分成了2份,其中的1份就是它的,3公顷的就是公顷,再把这1份平均分成3份,其中的1份就是公顷的,由此求解。
【解答】解:
整个阴影部分表示3公顷的,也就是,双阴影部分表示,即:×。
故选:C。
【点评】解决本题要注意题目要求的是多少公顷,而不是整个图形的几分之几,要结合分数的意义和分数乘法的意义求解。
二.填空题(共7小题)
7.【答案】;分子,分子,分母,分母。
【分析】依据题意结合图示可知,把大长方形的面积看作单位“1”,涂色部分占单位“1”的,把涂色部分的面积看作单位“1”,第二次涂色部分分别占涂色部分的几分之几,由此解答本题。
【解答】解:
我发现:分数乘分数,分子相乘的积作分子。
故答案为:分子,分子,分母。
【点评】本题考查的是分数乘法的意义的应用。
8.【答案】×。
【分析】通过图形看结果“?”处表示,从结果看,就是把单位“1”分成15份,并找出这个长方形的,即长方形中最上方的部分,在再把这个图形分成5份,找出其中的2份,据此解答。
【解答】解:把长方形平分成3份,找到其中的一份,即,然后把这个,再找到这3份其中2份,用,则这个2份占整个长方形的×=。
故答案为:×。
【点评】本题主要考查分数乘分数的结果在长方形中的推导过程。
9.【答案】×,转化。
【分析】根据图示可知,是把长方形平均分成3份,涂色其中的2份用分数表示;再把涂色的长方形平均分成5份,再涂色其中的4份就用分数表示,两次涂色的部分占长方形的几分之几就是求一个分数的几分之几是多少,用乘法计算,利用转化的思想直观的解释分数乘法的意义。
【解答】解:图中的网格部分,可以用算式×,这种转化的数学思想方法。
故答案为:×,转化。
【点评】本题考查了分数乘法的意义。
10.【答案】72。
【分析】由“甲是乙的”可知,单位“1”是乙,由“乙是丙的”可知,单位“1”是“丙”据此根据单位“1”的量=对应量÷对应分率,代入数值求出乙的值,进而求出丙的值,据此解答。
【解答】解:36=54
54=72
答:丙是72。
故答案为:72。
【点评】解答此题的关键是分清两个单位“1”的区别,求单位“1”的几分之几用乘法计算;已知单位“1”的几分之几是多少,求单位“1”用除法计算。
11.【答案】;;;0.4。
【分析】根据一个因数=积÷另一个因数,用1分别除以已知因数即可。
【解答】解:1÷=
3÷2=
2÷0.6=
1÷2.5=0.4
所以,=2=。
故答案为:;;;3.4。
【点评】考查了乘法各部分名称之间的关系的运用。
12.【答案】48;40;50。
【分析】求40千克增加后是多少千克,就是求40乘(1+)的积;求40千克增加千克后是多少千克,就是求40与的和;求40千克比多少千克少,就是求40除以(1﹣)的商。
【解答】解:40×(1+)
=40×
=48(千克)
40+=40
40÷(1﹣)
=40÷
=50(千克)
答:40千克增加后是48千克千克后是40,40千克比50千克少。
故答案为:48;40。
【点评】求比一个数多几分之几的数是多少,用乘法计算;已知比一个数少几分之几的数是多少,用除法计算。
13.【答案】见试题解答内容
【分析】35×表示把35看作单位“1”,平均分成7份,去其中的3份是多少,即求35的是多少.
【解答】解:35×表示把35看作单位“4”,去其中的3份是多少是多少.
故答案为:35,7,3,35,.
【点评】此题属于求一个数的几分之几是多少,解答关键是确定单位“1”,根据一个数乘分数的意义,用乘法解答.
三.判断题(共8小题)
14.【答案】×
【分析】要求比80千克多是多少千克,先用80乘求出多的质量,然后再加上80千克即可。
【解答】解:80×+80
=60+80
=140(千克)
答:比80千克多是140千克。
所以原题说法错误。
故答案为:×。
【点评】求比一个数多几分之几的数是多少,用乘法进行解答。
15.【答案】见试题解答内容
【分析】如果两个分数都大于1,它们的积就比两个分数大,可以通过举例证明.
【解答】解:两个分数相乘的积不一定小于每一个因数,例如:.
因此,分数乘分数,这种说法是错误的.
故答案为:×.
【点评】此题可用举例法进行解答.
16.【答案】×
【分析】分数乘分数:分子的乘积作分子,分母的乘积作分母,能约分的可以先约分,由此判断即可。
【解答】解:分数乘分数:分子的乘积作分子,分母的乘积作分母。
故答案为:×。
【点评】本题考查了分数乘分数的计算法则,要熟练掌握,灵活运算。
17.【答案】×
【分析】把2吨看作单位“1”,用去后,剩下的占原来的(1),根据一个数乘分数的意义,求出剩下的吨数与吨进行比较即可.
【解答】解:2×
=
=1(吨),
答:还剩1吨.
故答案为:×.
【点评】此题解答关键是确定单位“1”,求出剩下的占原来的几分之几,再根据一个数乘分数的意义,用乘法解答.
18.【答案】√
【分析】求一个数的几分之几是多少,用乘法计算,据此分别用60乘、40乘计算出60分米的和40分米的的长度,再进行比较。
【解答】解:60×=24(分米)
40×=24(分米)
答:60分米的和40分米的。
原题说法正确。
故答案为:√。
【点评】求一个数的几分之几是多少,用乘法计算。
19.【答案】√
【分析】先利用减法求出50米比40米多多少米,再利用多的数量÷40米,即可解答。
【解答】解:50﹣40=10(米)
10÷40=
因此50米比40米多,原题说法正确。
故答案为:√。
【点评】求一个数比另一个数多几分之几,用多出的数量除以单位“1”的数量。
20.【答案】√
【分析】根据分数乘法的计算法则,由于任何整数(0除外)都可以化成分母是1的假分数,分数乘整数或整数乘分数,都可以转化成分数乘以分数的形式,因此,在计算中,是用分数的分子和整数相乘的积作为分子,分母不变.在乘的过程中,如果有可以约分的数,可以先约分;分数乘以分数:用分子相乘的积作为分子,用分母相乘的积作为分母.为了使计算简便,在计算的过程中,能够约分的,要约分,判读即可。
【解答】解:根据由于任何整数(0除外)都可以化成分母是1的假分数,分数乘整数或整数乘分数,因此,是用分数的分子和整数相乘的积作为分子;在乘的过程中,可以先约分,用分母相乘的积作为分母,在计算的过程中,要约分。原题说法正确。
故答案为:√。
【点评】此题重点考查了分数乘法计算法则的掌握情况。
21.【答案】×
【分析】此题根据两个因数都大于1,或都小于1,以及它们的积,来加以判断.可以举出例子说明.
【解答】解:如果两个因数都大于1,积一定大于其中的任何一个因数;
如果两个因数小于1,积一定小于其中的任何一个因数;
例如8.1×0.2=0.002,积小于0.4和0.2.
故答案为:×.
【点评】此题考查了因数与积的关系,对于这样的问题,一般举出反例加以说明.
四.计算题(共1小题)
22.【答案】;;;;0;1;;;0;7。
【分析】异分母分数相加减,要先通分,化成同分母分数后再计算。
分数乘法的计算法则,分子相乘的积做分子,分母相乘的积做分母。
【解答】解:
= = = 1﹣=
0.2﹣=0 =1 = =
=0 ()×12=5
【点评】本题解题关键是熟练掌握异分母分数加减法和分数乘法的计算方法。
五.应用题(共6小题)
23.【答案】见试题解答内容
【分析】分数乘分数表示求一个分数的几分之几是多少,表示求的是多少,画图表示这个算式分两步,第一步,将长方形看作单位”1“,平均分成两份,涂其中的一份,表示它的;第二步,把涂色部分看作单位”1“,平均分成5份,涂其中的3份,表示的.
【解答】解:如图:
【点评】分数既可以表示具体的数,也可以表示两个量之间的关系,当表示关系时一定要分辨清谁是单位”1“.
24.【答案】。
【分析】根据题意,把乙数看作单位“1”,甲数是乙数的,丙数是甲数的,可以分别求出甲数和乙数,再根据求一个数是另一个数的几分之几用除法,即可解答。
【解答】解:把乙数看作单位“1”,甲数是乙数的
所以甲数:7×
丙数:=
答:丙数是乙数的。
【点评】熟练掌握求一个数是另一个数的几分之几用除法是解题的关键。
25.【答案】14岁。
【分析】把最大火炬手年龄看作单位“1”,年龄最小的火炬手是最大火炬手年龄的,用乘法计算,即可得最小火炬手今年多少岁。
【解答】解:84×=14(岁)
答:最小火炬手今年14岁。
【点评】本题主要考查了分数乘法应用题,已知一个数,求它的几分之几是多少,用乘法计算。
26.【答案】25人,20人。
【分析】航模小组和美术小组一共有45人,美术小组的人数是航模小组的,根据分数加法的意义,全部人数是航模小组人数的(1+),根据分数除法的意义,用总人数除以其占航模小组人数的分率,即得航模小组多少人,然后用减法求出美术小组人数。
【解答】解:45÷(1+)
=45×
=25(人)
45﹣25=20(人)
答:航模小组有25人,美术小组有20人。
【点评】首先根据已知条件求出总人数是航模小组人数的几分之几,进而求出航模小组人数是完成本题的关键。
27.【答案】见试题解答内容
【分析】一瓶果汁的净含量是升,求4瓶这样的果汁一共是多少升,用乘法计算;小华喝了这瓶果汁的,就是求的是多少,用乘法计算.
【解答】解:×4=3(升)
×=(升)
答:4瓶这样的果汁一共是5升,小华喝了这瓶果汁的升.
【点评】本题考查了分数乘法的意义:
1,分数乘整数:和整数乘法意义相同,就是求几个相同加数和的简便运算;
2,一个数乘分数:是求这个数的几分之几是多少.
28.【答案】2小时。
【分析】根据整数乘法的意义,北京飞往广州的时间乘2等于北京飞往拉萨的时间,根据分数乘法的意义,用飞往拉萨用的时间乘就是从北京飞往西安的时间。
【解答】解:4×2×
=8×
=2(小时)
答:从北京飞往西安大约用了5小时。
【点评】求一个数的几倍是多少,用这个数乘倍数;求一个数的几分之几是多少,用这个数乘分率。
