6.4平面向量的应用 高中数学人教A版(2019)必修第二册同步练习(含解析)
文档属性
| 名称 | 6.4平面向量的应用 高中数学人教A版(2019)必修第二册同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 555.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 18:14:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.4平面向量的应用高中数学人教 A版(2019)必修第二册
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知的内角,,的对边分别是,,,则“是钝角三角形”是“”的( )
A. 必要不充分条件 B. 充分不必要条件
C. 充要条件 D. 既不充分也不必要条件
2.“五月的风”是坐落在山东省青岛市五四广场的标志性雕塑,重达余吨,是我国目前最大的钢质城市雕塑,该雕塑充分展示了岛城的历史足迹.如图,现测量该雕塑的高度时,选取了与该雕塑底在同一平面内的两个测量基点与,测得,,,在点测得该雕塑顶端的仰角为,则该雕塑的高度约为参考数据:取
A. B. C. D.
3.在中,,,,则( )
A. B. C. D.
4.为测量两塔塔尖之间的距离,某数学建模活动小组构建了如图所示的几何模型.若平面,平面,,,,,,则塔尖之间的距离为( )
A. B. C. D.
5.已知的三个内角、、所对边分别为、、,则“”是“为直角三角形”的
( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
6.中,角,,的对边分别为,,,已知,,则的最大值为
( )
A. B. C. D.
7.在中,角,,的对边分别为,,,若,则( )
A. B. C. D.
8.在中,,,,则( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.的内角,,所对的边分别为,,,,,,则下列命题正确的是
( )
A. B. 的周长为
C. 的面积为 D. 的外接圆半径为
10.已知中,、、分别为角、、的对边,为的面积,则下列条件能使只有一个解的是( )
A. ,,
B. ,,
C.
D. ,,
11.的内角,,的对边分别为,,,则下列说法正确的是( )
A. 若,则
B. 若,则是钝角三角形
C. 若,,,则符合条件的有两个
D. 若,,则角的大小为
12.如图,在正八边形中,是其中心,且,则下列结论正确的是( )
A. B.
C. D. 在上的投影向量的模为
三、填空题:本题共4小题,每小题5分,共20分。
13.在中,角所对边分别为,,,,则 .
14.设为的外心,若,则的值为 .
15.在中,内角的对边分别为,,且,则外接圆的面积为 .
16.某次海上联合作战演习中,红方一艘侦察艇发现在北偏东方向,相距的水面上,有蓝方一艘小艇正以每小时的速度沿南偏东方向前进,若红方侦察艇以每小时的速度,沿北偏东方向拦截蓝方的小艇,若要在最短的时间内拦截住,则角的余弦值为 .
四、解答题:本题共4小题,共48分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知的内角,,所对的边分别为,且向量与
平行.
求
若,,求的面积.
18.本小题分
如图,、是海面上位于东西方向相距海里的两个观测点,现位于点北偏东,点北偏西的点有一艘轮船发出求救信号,位于点南偏西且与点相距海里的点的救援船立即前往营救,其航行速度为海里小时,试求:
轮船与观测点的距离
救援船到达点所需要的时间.
19.本小题分
如图,某城市有一条公路从正西方通过市中心后转向东偏北角方向的位于该市的某大学与市中心的距离,且现要修筑一条铁路,在上设一站,在上设一站,铁路在部分为直线段,且经过大学其中,,.
求大学与站的距离;
求铁路段的长.
20.本小题分
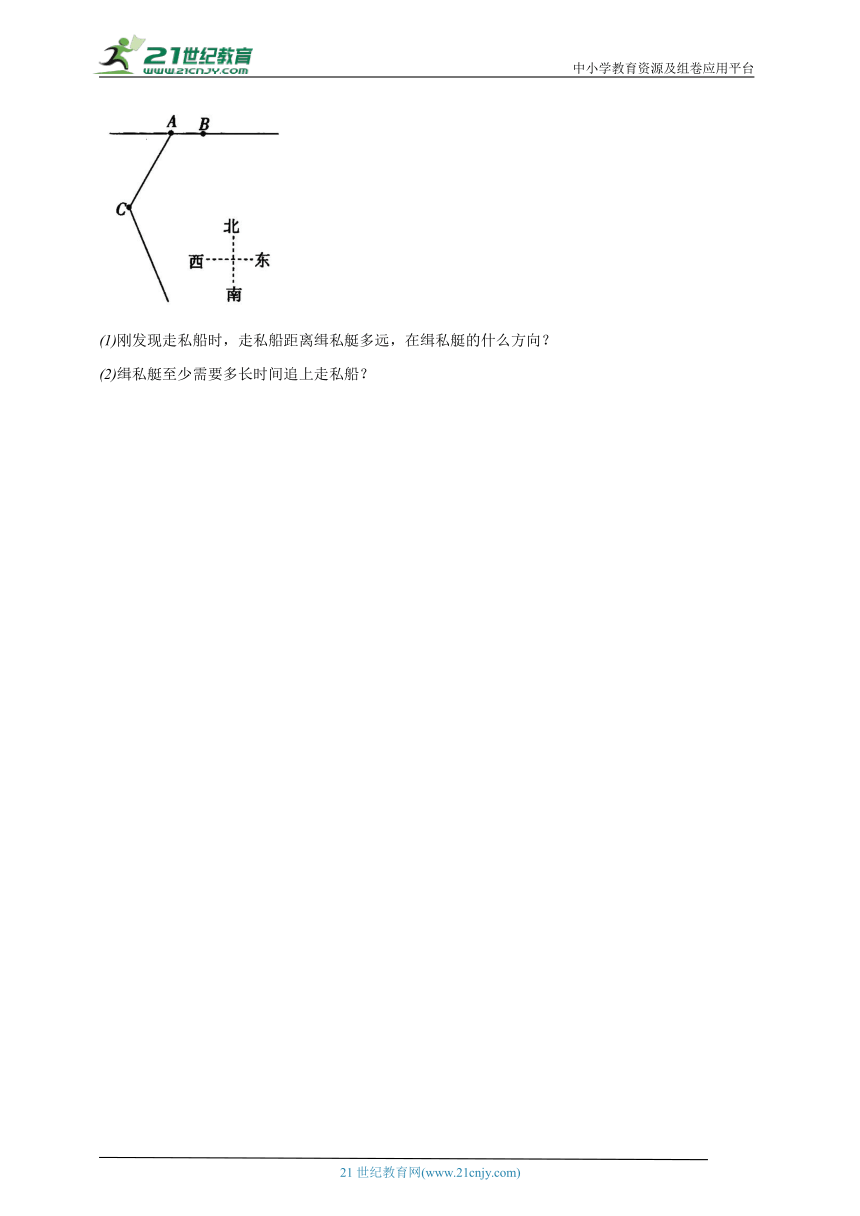
如图,在海岸边点的观测站发现南偏西方向上,距离点海里的处有一艘走私船,立刻通知了停在的正东方向上,且距离点海里的处的缉私艇,缉私艇立刻奉命以海里时的速度追截走私船,此时,走私船正以海里时的速度从处沿南偏东方向逃窜.
刚发现走私船时,走私船距离缉私艇多远,在缉私艇的什么方向?
缉私艇至少需要多长时间追上走私船?
答案和解析
1.【答案】
【解析】【分析】
本题考查充分、必要条件的判断,利用余弦定理判断三角形的形状,属于中档题.
利用余弦定理和充分、必要条件的定义即可判断.
【解答】
解:若中为钝角,
则为锐角,,
即有,
故充分性不成立
若,
由余弦定理得,
即为钝角,
故必要性成立.
故选:.
2.【答案】
【解析】【分析】
本题考查了利用正弦定理解决高度问题,属于中档题.
利用正弦定理,结合题意计算即可得解.
【解答】
解:由题意得,
在中,由,
得,
在中,.
故选C.
3.【答案】
【解析】【分析】
本题考查余弦定理,考查运算求解能力,难度一般.
先由已知条件应用余弦定理求出,再利用余弦定理即可求出.
【解答】
解:由余弦定理可得,
解得.
在中,,
由余弦定理可得
故选A.
4.【答案】
【解析】【分析】
本题考查解三角形,数形结合思想,考查学生的计算能力,属于中档题.
通过所给条件依次求出,,再由余弦定理可求得.
【解答】
解:由题得,在中,,则,
在中,,
则在中,由余弦定理可得,
则.
故选:.
5.【答案】
【解析】【分析】
本题考查了正弦定理、诱导公式、两角和的正弦公式的简单运用,充分条件、必要条件的判断,属于中档题.
由已知结合正弦定理可得,利用三角形的内角和及和角的正弦公式化简可得为直角,结合充分条件及必要条件进行判断即可.
【解答】
解:因为,
由正弦定理可得, 即,
所以,
所以,
因为,所以,,
则,为直角三角形,
但为直角三角形时不一定是,
所以是为直角三角形的充分不必要条件.
故选:.
6.【答案】
【解析】【分析】
本题考查了正弦定理、余弦定理的应用,三角形的面积公式,以及利用基本不等式求最值问题,考查化简、变形能力,属于较难题.
由正弦定理和条件得,由余弦定理及基本不等式得到,根据面积公式求出面积的最大值.
【解答】
解:,
,又,
则,,
由余弦定理及,
得,
,
又,得,当且仅当时取等号,
的面积.
当时,的面积有最大值,
故选D
7.【答案】
【解析】【分析】
本题主要考查了正弦定理和余弦定理在解三角形中的综合应用,考查了运算求解能力和转化思想,属于基础题.
由正弦定理化简已知等式可得,再根据余弦定理可得,结合范围,可得的值.
【解答】
解:因为,
所以由正弦定理可得,即,
可得,
因为,
所以.
故选:.
8.【答案】
【解析】【分析】
本题主要考查了余弦定理的应用,熟练掌握余弦定理是解本题的关键,属于基础题.
先根据余弦定理求出,再代入余弦定理求出结论.
【解答】
解:在中,,,,
由余弦定理可得,故AB,
.
故选A.
9.【答案】
【解析】【分析】
本题考查正弦定理,余弦定理,两角和与差的正弦公式、二倍角公式,考查化简、计算能力,属于中档题.
根据内角和定理、诱导公式、两角和与差的正弦公式、二倍角公式化简已知的式子,由化简的结果进行分类讨论,由内角的范围、余弦定理分别解三角形,根据结果分别判断、;利用直角三角形的面积公式求出的面积判断;根据正弦定理判断.
【解答】
解:由得,,
,
,
化简得,,则,
或,
当,即时,由,得,
,,则;
当时,由正弦定理得,,
,,
由余弦定理得,
则,解得,则,
此时满足,即.
对于选项A,当时,,故A错误;
对于选项B,当或时,的周长为:,故B正确;
对于选项C,当时,的面积;
当时,的面积,成立,故C正确;
对于选项D,当或时,
由正弦定理得,得,故D错误,
综上可得,命题正确的是,
故选BC.
10.【答案】
【解析】【分析】
本题考查了利用余弦定理理解三角形,正弦定理及变形,三角形面积公式,两角和与差的正弦公式,属于一般题.
根据两边之和与两边之差与第三边的关系可判断,利用正弦和余弦定理实现边角互化可判断,根据面积公式可得,进而得角有两个值,可判断,根据内角和即可判断.
【解答】
解:对于:由三角形三边关系可得:,所以,因为,故,故A正确.
对于:由,
故,
可得:,,由此解得,
故三角形唯一,B正确,
对于:或者,故三角形不唯一,C错误.
对于:,,故,两边及其夹角,此三角形唯一,故D正确.
故选:.
11.【答案】
【解析】【分析】
本题考查的知识要点:三角函数关系式的恒等变换,正弦定理、余弦定理的应用,主要考查学生的运算能力和数学思维能力,属于基础题.
直接利用三角函数关系式的恒等变换和正弦定理、余弦定理的应用判断、、、的结论.
【解答】
解:中,角,,所对的边分别为,,.
对于:当时,所以,根据正弦定理,
整理得,故A正确;
对于:若,
则由正弦定理可得,由余弦定理可得,
可得为钝角,则是钝角三角形,故B正确;
对于:由于,,,
利用余弦定理:,
解得,可得有一解,故C错误;
对于:由正弦定理可知,,
可得,由于,可得,故D正确.
故答案选:.
12.【答案】
【解析】【分析】
本题考查平面向量的数量积、线性运算、模以及投影的计算,属于中档题.
根题平面向量的相关概念,对各选项逐一分析,即可得到答案.
【解答】
解:对于,因为为正八边形,为其中心,
故,
,,故A正确;
对于,与的夹角为,又,
所以,故B正确
对于,,,
在中,由余弦定理可得
,
,故C错误
对于,在上的投影向量的模为 ,
显然不为,故,故D错误.
故选AB.
13.【答案】
【解析】【分析】
本题考查利用余弦定理、正弦定理解三角形,属于基础题.
先根据余弦定理得到 ,再由正弦定理即可求得答案.
【解答】
解:由余弦定理得到 ,
即 ,故
由正弦定理可得: .
故答案为:.
14.【答案】
【解析】【分析】
本题考查利用正余弦定理解三角形,向量的线性运算,属于中档题.
设外接圆的半径为,由已知条件可得,即且,取的中点,连接可得,计算的值,再由余弦定理求出,在中,由正弦定理即可求解.
【解答】
解:设外接圆的半径为,
因为,所以,
所以,且,如图,
取的中点,连接,则,
因为,所以,即,
所以
,
在中由余弦定理可得:
,
在中,由正弦定理可得:,
故答案为:.
15.【答案】
【解析】【分析】
本题考查了正弦定理和二倍角公式及其应用 ,属于中档题.
由正弦定理及二倍角公式可求得角的余弦值,进而求得角的正弦值以及外接圆半径,故可得解.
【解答】
解:在中,由正弦定理得,则,
,,
,
因为,
,
设外接圆的半径为,
由正弦定理得,,
故外接圆的面积为.
故答案为.
16.【答案】
【解析】【分析】
本题考查正弦定理和余弦定理解三角形在实际中的应用,属于中档题.
结合题意设红方侦察艇经过 小时后在 处追上蓝方的小艇,根据余弦定理求得的值,再用正弦定理即可求解角的正弦值,即可求其余弦值.
【解答】
解:如图,设红方侦察艇经过 小时后在 处追上蓝方的小艇,
则,,,.
根据余弦定理得,解得.
故AC,.
根据正弦定理得,解得.
所以,
故答案为:.
17.【答案】解:由题意得: ,所以 ,
由正弦定理 得: ,
又因为 ,则有 ,
又 ,所以 .
由余弦定理得: ,
又 , , ,
所以 ,解得 ,
则 的面积 .
【解析】本题考查了余弦定理,向量平行的坐标表示,三角形面积公式,属于一般题.
根据向量平行的坐标表示 得 ,再根据正弦定理进行边角互化即可求得角 ;
根据余弦定理 ,及 , , ,配方可求解出 ,再利用三角形的面积公式 求解即可.
18.【答案】 解:由在的北偏东,在的北偏西,
,,,
由正弦定理得,
,
又,
代入上式得:海里,
答:轮船与观测点的距离为海里;
中,海里,海里,,
,
,解得海里,
小时,
答:救援船到达所需的时间为小时.
【解析】本题考查了正弦、余弦定理的实际应用问题,是中档题.
由方位角求得、,利用三角形内角和定理与正弦定理求得的值;
中,利用余弦定理求得的值,再计算救援船到达所需的时间.
19.【答案】解:在中,,,且,,
由余弦定理可得:
,
,
大学与站的距离为;
,且为锐角,
,
在中,由正弦定理可得:,
即,
,由图可知为锐角,
,
,
,
,,
,
又,
,
在中,,
由正弦定理可得:,
即,
解得,
铁路段的长为
【解析】本题考查正弦定理、余弦定理、解三角形的实际应用,属于中档题.
在中,利用已知及余弦定理即可解得的值;
由,且为锐角,可求,由正弦定理可得,结合,可求,,,,结合,由正弦定理即可解得的值.
20.【答案】解:由题意可知,,.
在中,由余弦定理得.
由正弦定理得,解得,所以.
故刚发现走私船时,走私船距缉私艇海里,在缉私艇的南偏西方向上.
如图,设小时后缉私艇在处追上走私船,则,
在中,由正弦定理得
解得,则,所以是等腰三角形
,即.
故缉私艇至少需要小时追上走私船.
【解析】本题考查解三角形的实际应用,属于中档题.
利用余弦定理求,利用正弦定理求即可
利用正弦定理判断出是等腰三角形,即可求出所需的最少时间.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.4平面向量的应用高中数学人教 A版(2019)必修第二册
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知的内角,,的对边分别是,,,则“是钝角三角形”是“”的( )
A. 必要不充分条件 B. 充分不必要条件
C. 充要条件 D. 既不充分也不必要条件
2.“五月的风”是坐落在山东省青岛市五四广场的标志性雕塑,重达余吨,是我国目前最大的钢质城市雕塑,该雕塑充分展示了岛城的历史足迹.如图,现测量该雕塑的高度时,选取了与该雕塑底在同一平面内的两个测量基点与,测得,,,在点测得该雕塑顶端的仰角为,则该雕塑的高度约为参考数据:取
A. B. C. D.
3.在中,,,,则( )
A. B. C. D.
4.为测量两塔塔尖之间的距离,某数学建模活动小组构建了如图所示的几何模型.若平面,平面,,,,,,则塔尖之间的距离为( )
A. B. C. D.
5.已知的三个内角、、所对边分别为、、,则“”是“为直角三角形”的
( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
6.中,角,,的对边分别为,,,已知,,则的最大值为
( )
A. B. C. D.
7.在中,角,,的对边分别为,,,若,则( )
A. B. C. D.
8.在中,,,,则( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.的内角,,所对的边分别为,,,,,,则下列命题正确的是
( )
A. B. 的周长为
C. 的面积为 D. 的外接圆半径为
10.已知中,、、分别为角、、的对边,为的面积,则下列条件能使只有一个解的是( )
A. ,,
B. ,,
C.
D. ,,
11.的内角,,的对边分别为,,,则下列说法正确的是( )
A. 若,则
B. 若,则是钝角三角形
C. 若,,,则符合条件的有两个
D. 若,,则角的大小为
12.如图,在正八边形中,是其中心,且,则下列结论正确的是( )
A. B.
C. D. 在上的投影向量的模为
三、填空题:本题共4小题,每小题5分,共20分。
13.在中,角所对边分别为,,,,则 .
14.设为的外心,若,则的值为 .
15.在中,内角的对边分别为,,且,则外接圆的面积为 .
16.某次海上联合作战演习中,红方一艘侦察艇发现在北偏东方向,相距的水面上,有蓝方一艘小艇正以每小时的速度沿南偏东方向前进,若红方侦察艇以每小时的速度,沿北偏东方向拦截蓝方的小艇,若要在最短的时间内拦截住,则角的余弦值为 .
四、解答题:本题共4小题,共48分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知的内角,,所对的边分别为,且向量与
平行.
求
若,,求的面积.
18.本小题分
如图,、是海面上位于东西方向相距海里的两个观测点,现位于点北偏东,点北偏西的点有一艘轮船发出求救信号,位于点南偏西且与点相距海里的点的救援船立即前往营救,其航行速度为海里小时,试求:
轮船与观测点的距离
救援船到达点所需要的时间.
19.本小题分
如图,某城市有一条公路从正西方通过市中心后转向东偏北角方向的位于该市的某大学与市中心的距离,且现要修筑一条铁路,在上设一站,在上设一站,铁路在部分为直线段,且经过大学其中,,.
求大学与站的距离;
求铁路段的长.
20.本小题分
如图,在海岸边点的观测站发现南偏西方向上,距离点海里的处有一艘走私船,立刻通知了停在的正东方向上,且距离点海里的处的缉私艇,缉私艇立刻奉命以海里时的速度追截走私船,此时,走私船正以海里时的速度从处沿南偏东方向逃窜.
刚发现走私船时,走私船距离缉私艇多远,在缉私艇的什么方向?
缉私艇至少需要多长时间追上走私船?
答案和解析
1.【答案】
【解析】【分析】
本题考查充分、必要条件的判断,利用余弦定理判断三角形的形状,属于中档题.
利用余弦定理和充分、必要条件的定义即可判断.
【解答】
解:若中为钝角,
则为锐角,,
即有,
故充分性不成立
若,
由余弦定理得,
即为钝角,
故必要性成立.
故选:.
2.【答案】
【解析】【分析】
本题考查了利用正弦定理解决高度问题,属于中档题.
利用正弦定理,结合题意计算即可得解.
【解答】
解:由题意得,
在中,由,
得,
在中,.
故选C.
3.【答案】
【解析】【分析】
本题考查余弦定理,考查运算求解能力,难度一般.
先由已知条件应用余弦定理求出,再利用余弦定理即可求出.
【解答】
解:由余弦定理可得,
解得.
在中,,
由余弦定理可得
故选A.
4.【答案】
【解析】【分析】
本题考查解三角形,数形结合思想,考查学生的计算能力,属于中档题.
通过所给条件依次求出,,再由余弦定理可求得.
【解答】
解:由题得,在中,,则,
在中,,
则在中,由余弦定理可得,
则.
故选:.
5.【答案】
【解析】【分析】
本题考查了正弦定理、诱导公式、两角和的正弦公式的简单运用,充分条件、必要条件的判断,属于中档题.
由已知结合正弦定理可得,利用三角形的内角和及和角的正弦公式化简可得为直角,结合充分条件及必要条件进行判断即可.
【解答】
解:因为,
由正弦定理可得, 即,
所以,
所以,
因为,所以,,
则,为直角三角形,
但为直角三角形时不一定是,
所以是为直角三角形的充分不必要条件.
故选:.
6.【答案】
【解析】【分析】
本题考查了正弦定理、余弦定理的应用,三角形的面积公式,以及利用基本不等式求最值问题,考查化简、变形能力,属于较难题.
由正弦定理和条件得,由余弦定理及基本不等式得到,根据面积公式求出面积的最大值.
【解答】
解:,
,又,
则,,
由余弦定理及,
得,
,
又,得,当且仅当时取等号,
的面积.
当时,的面积有最大值,
故选D
7.【答案】
【解析】【分析】
本题主要考查了正弦定理和余弦定理在解三角形中的综合应用,考查了运算求解能力和转化思想,属于基础题.
由正弦定理化简已知等式可得,再根据余弦定理可得,结合范围,可得的值.
【解答】
解:因为,
所以由正弦定理可得,即,
可得,
因为,
所以.
故选:.
8.【答案】
【解析】【分析】
本题主要考查了余弦定理的应用,熟练掌握余弦定理是解本题的关键,属于基础题.
先根据余弦定理求出,再代入余弦定理求出结论.
【解答】
解:在中,,,,
由余弦定理可得,故AB,
.
故选A.
9.【答案】
【解析】【分析】
本题考查正弦定理,余弦定理,两角和与差的正弦公式、二倍角公式,考查化简、计算能力,属于中档题.
根据内角和定理、诱导公式、两角和与差的正弦公式、二倍角公式化简已知的式子,由化简的结果进行分类讨论,由内角的范围、余弦定理分别解三角形,根据结果分别判断、;利用直角三角形的面积公式求出的面积判断;根据正弦定理判断.
【解答】
解:由得,,
,
,
化简得,,则,
或,
当,即时,由,得,
,,则;
当时,由正弦定理得,,
,,
由余弦定理得,
则,解得,则,
此时满足,即.
对于选项A,当时,,故A错误;
对于选项B,当或时,的周长为:,故B正确;
对于选项C,当时,的面积;
当时,的面积,成立,故C正确;
对于选项D,当或时,
由正弦定理得,得,故D错误,
综上可得,命题正确的是,
故选BC.
10.【答案】
【解析】【分析】
本题考查了利用余弦定理理解三角形,正弦定理及变形,三角形面积公式,两角和与差的正弦公式,属于一般题.
根据两边之和与两边之差与第三边的关系可判断,利用正弦和余弦定理实现边角互化可判断,根据面积公式可得,进而得角有两个值,可判断,根据内角和即可判断.
【解答】
解:对于:由三角形三边关系可得:,所以,因为,故,故A正确.
对于:由,
故,
可得:,,由此解得,
故三角形唯一,B正确,
对于:或者,故三角形不唯一,C错误.
对于:,,故,两边及其夹角,此三角形唯一,故D正确.
故选:.
11.【答案】
【解析】【分析】
本题考查的知识要点:三角函数关系式的恒等变换,正弦定理、余弦定理的应用,主要考查学生的运算能力和数学思维能力,属于基础题.
直接利用三角函数关系式的恒等变换和正弦定理、余弦定理的应用判断、、、的结论.
【解答】
解:中,角,,所对的边分别为,,.
对于:当时,所以,根据正弦定理,
整理得,故A正确;
对于:若,
则由正弦定理可得,由余弦定理可得,
可得为钝角,则是钝角三角形,故B正确;
对于:由于,,,
利用余弦定理:,
解得,可得有一解,故C错误;
对于:由正弦定理可知,,
可得,由于,可得,故D正确.
故答案选:.
12.【答案】
【解析】【分析】
本题考查平面向量的数量积、线性运算、模以及投影的计算,属于中档题.
根题平面向量的相关概念,对各选项逐一分析,即可得到答案.
【解答】
解:对于,因为为正八边形,为其中心,
故,
,,故A正确;
对于,与的夹角为,又,
所以,故B正确
对于,,,
在中,由余弦定理可得
,
,故C错误
对于,在上的投影向量的模为 ,
显然不为,故,故D错误.
故选AB.
13.【答案】
【解析】【分析】
本题考查利用余弦定理、正弦定理解三角形,属于基础题.
先根据余弦定理得到 ,再由正弦定理即可求得答案.
【解答】
解:由余弦定理得到 ,
即 ,故
由正弦定理可得: .
故答案为:.
14.【答案】
【解析】【分析】
本题考查利用正余弦定理解三角形,向量的线性运算,属于中档题.
设外接圆的半径为,由已知条件可得,即且,取的中点,连接可得,计算的值,再由余弦定理求出,在中,由正弦定理即可求解.
【解答】
解:设外接圆的半径为,
因为,所以,
所以,且,如图,
取的中点,连接,则,
因为,所以,即,
所以
,
在中由余弦定理可得:
,
在中,由正弦定理可得:,
故答案为:.
15.【答案】
【解析】【分析】
本题考查了正弦定理和二倍角公式及其应用 ,属于中档题.
由正弦定理及二倍角公式可求得角的余弦值,进而求得角的正弦值以及外接圆半径,故可得解.
【解答】
解:在中,由正弦定理得,则,
,,
,
因为,
,
设外接圆的半径为,
由正弦定理得,,
故外接圆的面积为.
故答案为.
16.【答案】
【解析】【分析】
本题考查正弦定理和余弦定理解三角形在实际中的应用,属于中档题.
结合题意设红方侦察艇经过 小时后在 处追上蓝方的小艇,根据余弦定理求得的值,再用正弦定理即可求解角的正弦值,即可求其余弦值.
【解答】
解:如图,设红方侦察艇经过 小时后在 处追上蓝方的小艇,
则,,,.
根据余弦定理得,解得.
故AC,.
根据正弦定理得,解得.
所以,
故答案为:.
17.【答案】解:由题意得: ,所以 ,
由正弦定理 得: ,
又因为 ,则有 ,
又 ,所以 .
由余弦定理得: ,
又 , , ,
所以 ,解得 ,
则 的面积 .
【解析】本题考查了余弦定理,向量平行的坐标表示,三角形面积公式,属于一般题.
根据向量平行的坐标表示 得 ,再根据正弦定理进行边角互化即可求得角 ;
根据余弦定理 ,及 , , ,配方可求解出 ,再利用三角形的面积公式 求解即可.
18.【答案】 解:由在的北偏东,在的北偏西,
,,,
由正弦定理得,
,
又,
代入上式得:海里,
答:轮船与观测点的距离为海里;
中,海里,海里,,
,
,解得海里,
小时,
答:救援船到达所需的时间为小时.
【解析】本题考查了正弦、余弦定理的实际应用问题,是中档题.
由方位角求得、,利用三角形内角和定理与正弦定理求得的值;
中,利用余弦定理求得的值,再计算救援船到达所需的时间.
19.【答案】解:在中,,,且,,
由余弦定理可得:
,
,
大学与站的距离为;
,且为锐角,
,
在中,由正弦定理可得:,
即,
,由图可知为锐角,
,
,
,
,,
,
又,
,
在中,,
由正弦定理可得:,
即,
解得,
铁路段的长为
【解析】本题考查正弦定理、余弦定理、解三角形的实际应用,属于中档题.
在中,利用已知及余弦定理即可解得的值;
由,且为锐角,可求,由正弦定理可得,结合,可求,,,,结合,由正弦定理即可解得的值.
20.【答案】解:由题意可知,,.
在中,由余弦定理得.
由正弦定理得,解得,所以.
故刚发现走私船时,走私船距缉私艇海里,在缉私艇的南偏西方向上.
如图,设小时后缉私艇在处追上走私船,则,
在中,由正弦定理得
解得,则,所以是等腰三角形
,即.
故缉私艇至少需要小时追上走私船.
【解析】本题考查解三角形的实际应用,属于中档题.
利用余弦定理求,利用正弦定理求即可
利用正弦定理判断出是等腰三角形,即可求出所需的最少时间.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
