鲁教版九年级数学下册第5章5.7切线长定理同步训练题(含答案)
文档属性
| 名称 | 鲁教版九年级数学下册第5章5.7切线长定理同步训练题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 196.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-26 07:48:32 | ||
图片预览

文档简介
鲁教版九年级数学下册第5章5.7切线长定理同步训练题(含答案)
一.选择题(共10小题)
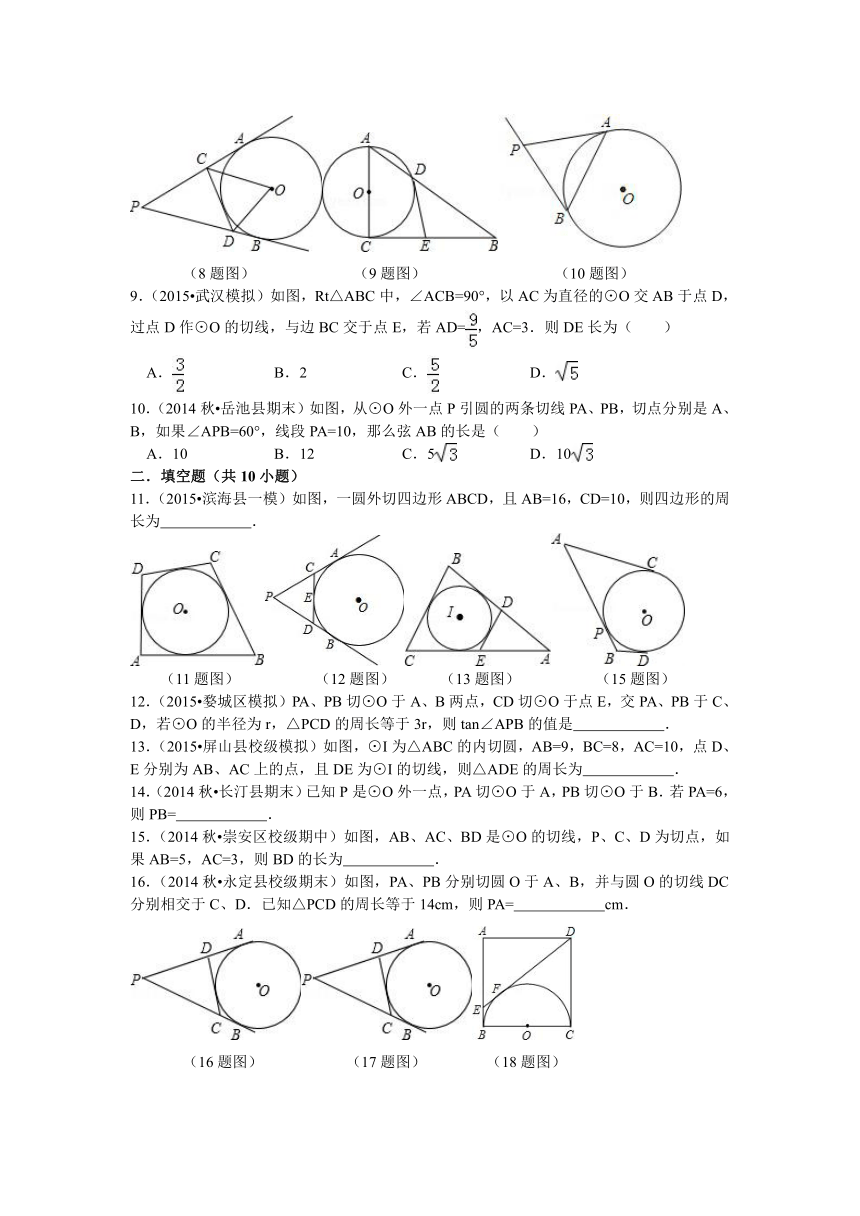
1.(2014春 鹿城区校级期末)如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为( )
A.120° B.60° C.30° D.45°
(1题图) (2题图) (3题图)
2.(2014秋 安顺期末)如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )
A.15 B.12 C.20 D.30
3.(2015 秦皇岛校级模拟)如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为( )
A.32 B.34 C.36 D.38
4.(2015 齐齐哈尔一模)如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12 B.24 C.8 D.6
(4题图) (5题图) (6题图) (7题图)
5.(2014秋 鄞州区期末)如图,PA、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为( )
A.40° B.140° C.70° D.80°
6.(2014秋 亭湖区校级月考)如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的值是( )
A. B. C. D.
7.(2015 高港区二模)矩形ABCD中,AB=4,AD=3,以AB为直径在矩形内作半圆.DE切⊙O于点E(如图),则tan∠CDF的值为( )
A. B. C. D.
8.(2014秋 夏津县校级期末)如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为( )
A.5,(90°+∠P) B.7,90°+ C.10,90°﹣∠P D.10,90°+∠P
(8题图) (9题图) (10题图)
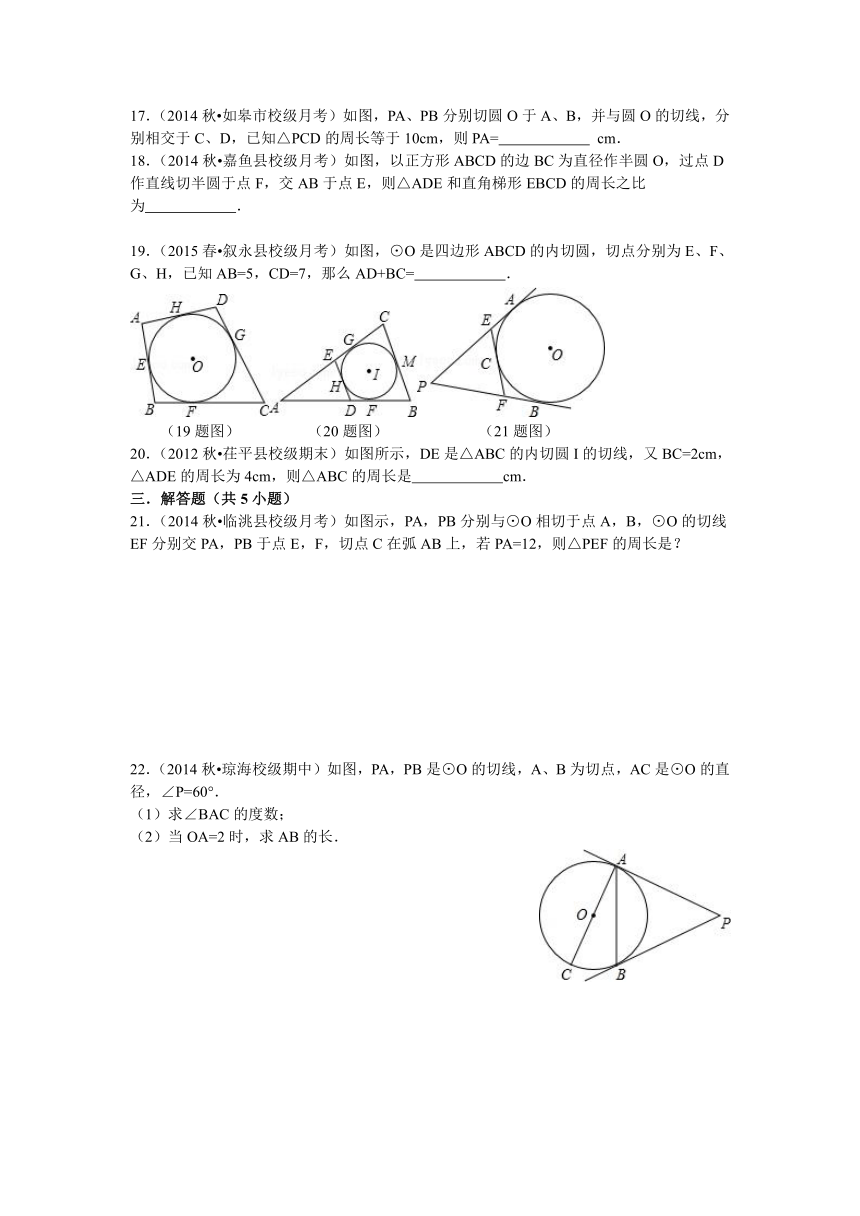
9.(2015 武汉模拟)如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线,与边BC交于点E,若AD=,AC=3.则DE长为( )
A. B.2 C. D.
10.(2014秋 岳池县期末)如图,从⊙O外一点P引圆的两条切线PA、PB,切点分别是A、B,如果∠APB=60°,线段PA=10,那么弦AB的长是( )
A.10 B.12 C.5 D.10
二.填空题(共10小题)
11.(2015 滨海县一模)如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为 .
(11题图) (12题图) (13题图) (15题图)
12.(2015 婺城区模拟)PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是 .
13.(2015 屏山县校级模拟)如图,⊙I为△ABC的内切圆,AB=9,BC=8,AC=10,点D、E分别为AB、AC上的点,且DE为⊙I的切线,则△ADE的周长为 .
14.(2014秋 长汀县期末)已知P是⊙O外一点,PA切⊙O于A,PB切⊙O于B.若PA=6,则PB= .
15.(2014秋 崇安区校级期中)如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为 .
16.(2014秋 永定县校级期末)如图,PA、PB分别切圆O于A、B,并与圆O的切线DC分别相交于C、D.已知△PCD的周长等于14cm,则PA= cm.
(16题图) (17题图) (18题图)
17.(2014秋 如皋市校级月考)如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA= cm.
18.(2014秋 嘉鱼县校级月考)如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB于点E,则△ADE和直角梯形EBCD的周长之比为 .
19.(2015春 叙永县校级月考)如图,⊙O是四边形ABCD的内切圆,切点分别为E、F、G、H,已知AB=5,CD=7,那么AD+BC= .
(19题图) (20题图) (21题图)
20.(2012秋 茌平县校级期末)如图所示,DE是△ABC的内切圆I的切线,又BC=2cm,△ADE的周长为4cm,则△ABC的周长是 cm.
三.解答题(共5小题)
21.(2014秋 临洮县校级月考)如图示,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA=12,则△PEF的周长是?
22.(2014秋 琼海校级期中)如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
23.(2014秋 张家港市期末)如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E;
(1)求证:BE=CE;
(2)若以O、D、E、C为顶点的四边形是正方形,⊙O的半径为r,求△ABC的面积;
(3)若EC=4,BD=,求⊙O的半径OC的长.
24.(2015 潍坊模拟)如图,PA、PB切⊙O于A、B,若∠APB=60°,⊙O半径为3,求阴影部分面积.
25.(2014秋 仙游县期中)已知:AB为⊙O的直径,∠A=∠B=90°,DE与⊙O相切于E,⊙O的半径为,AD=2.
①求BC的长;
②延长AE交BC的延长线于G点,求EG的长.
鲁教版九年级数学下册第5章5.7切线长定理同步训练题参考答案
一.选择题(共10小题)
1.B 2.D 3.B 4.D 5.C 6.A 7.B 8.C 9.B 10.A
二.填空题(共10小题)
11.52 12. 13.11 14.6 15.2 16.7 17.5
18.6:7 19.12 20.8
三.解答题(共5小题)
21.解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在弧AB上,
∴AE=CE,FB=CF,PA=PB=12,
∴△PEF的周长=PE+EF+PF=PA+PB=24.
22.解:(1)∵PA,PB是⊙O的切线,∴AP=BP,
∵∠P=60°,∴∠PAB=60°,
∵AC是⊙O的直径,∴∠PAC=90°,∴∠BAC=90°﹣60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
∴OP=4,
由勾股定理得:,
∵AP=BP,∠APB=60°,
∴△APB是等边三角形,
∴.
23.(1)证明:连接CD,由AC是直径知CD⊥AB;
DE、CE都是切线,所以DE=CE,∠EDC=∠ECD;
又∠B+∠ECD=90°,∠BDE+∠EDC=90°;
所以∠B=∠BDE,所以BE=DE,从而BE=CE;
(2)解:连接OD,
当以O、D、E、C为顶点的四边形是正方形时,DE=EC=OC=OD=r;
从而BE=r,即△ABC是一个等腰直角三角形;
AC=AB=2r,S△ABC=2r2;
(3)解:若EC=4,BD=4,则BC=8;
在Rt△BDC中,cos∠CBD==;所以∠CBD=30°;
在Rt△ABC中,=tan30°,即AC=BCtan30°=8×=,OC==;
另解:设OC=r,AD=x;由EC=4,BD=4得BC=8,DC=4;
则:,解得;即OC=.
(23题图) (24题图) (25题图)
24.解:连接PO与AO,
∵PA、PB切⊙O于A、B,若∠APB=60°,∴OA⊥PA,∠APO=∠APB=30°,
∴∠AOP=60°,
∵⊙O半径为3,∴OA=3,PO=6,∴PA==3,
∴S△PAO=AO PA=×3×3=,S扇形AOC==π,
∴S阴影=2×(S△PAO﹣S扇形AOC)=2×(﹣π)=9﹣3π.
∴阴影部分面积为:9﹣3π.
25.解:①过点D作DF⊥BC于点F,
∵AB为⊙O的直径,∠A=∠B=90°,
∴四边形ABFD是矩形,AD与BC是⊙O的切线,
∴DF=AB=2,BF=AD=2,
∵DE与⊙O相切,
∴DE=AD=2,CE=BC,
设BC=x,则CF=BC﹣BF=x﹣2,DC=DE+CE=2+x,
在Rt△DCF中,DC2=CF2+DF2,即(2+x)2=(x﹣2)2+(2)2,解得:x=,
即BC=;
②∵AB为⊙O的直径,∠A=∠B=90°,∴AD∥BC,∴△ADE∽△GCE,
∴AD:CG=DE:CE,AE:EG=AD:CG,
∵AD=DE=2,∴CG=CE=BC=,∴BG=BC+CG=5,∴AE:EG=4:5,
在Rt△ABG中,AG==3,∴EG=AG=.
一.选择题(共10小题)
1.(2014春 鹿城区校级期末)如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为( )
A.120° B.60° C.30° D.45°
(1题图) (2题图) (3题图)
2.(2014秋 安顺期末)如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )
A.15 B.12 C.20 D.30
3.(2015 秦皇岛校级模拟)如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为( )
A.32 B.34 C.36 D.38
4.(2015 齐齐哈尔一模)如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12 B.24 C.8 D.6
(4题图) (5题图) (6题图) (7题图)
5.(2014秋 鄞州区期末)如图,PA、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为( )
A.40° B.140° C.70° D.80°
6.(2014秋 亭湖区校级月考)如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的值是( )
A. B. C. D.
7.(2015 高港区二模)矩形ABCD中,AB=4,AD=3,以AB为直径在矩形内作半圆.DE切⊙O于点E(如图),则tan∠CDF的值为( )
A. B. C. D.
8.(2014秋 夏津县校级期末)如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为( )
A.5,(90°+∠P) B.7,90°+ C.10,90°﹣∠P D.10,90°+∠P
(8题图) (9题图) (10题图)
9.(2015 武汉模拟)如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线,与边BC交于点E,若AD=,AC=3.则DE长为( )
A. B.2 C. D.
10.(2014秋 岳池县期末)如图,从⊙O外一点P引圆的两条切线PA、PB,切点分别是A、B,如果∠APB=60°,线段PA=10,那么弦AB的长是( )
A.10 B.12 C.5 D.10
二.填空题(共10小题)
11.(2015 滨海县一模)如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为 .
(11题图) (12题图) (13题图) (15题图)
12.(2015 婺城区模拟)PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是 .
13.(2015 屏山县校级模拟)如图,⊙I为△ABC的内切圆,AB=9,BC=8,AC=10,点D、E分别为AB、AC上的点,且DE为⊙I的切线,则△ADE的周长为 .
14.(2014秋 长汀县期末)已知P是⊙O外一点,PA切⊙O于A,PB切⊙O于B.若PA=6,则PB= .
15.(2014秋 崇安区校级期中)如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为 .
16.(2014秋 永定县校级期末)如图,PA、PB分别切圆O于A、B,并与圆O的切线DC分别相交于C、D.已知△PCD的周长等于14cm,则PA= cm.
(16题图) (17题图) (18题图)
17.(2014秋 如皋市校级月考)如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA= cm.
18.(2014秋 嘉鱼县校级月考)如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB于点E,则△ADE和直角梯形EBCD的周长之比为 .
19.(2015春 叙永县校级月考)如图,⊙O是四边形ABCD的内切圆,切点分别为E、F、G、H,已知AB=5,CD=7,那么AD+BC= .
(19题图) (20题图) (21题图)
20.(2012秋 茌平县校级期末)如图所示,DE是△ABC的内切圆I的切线,又BC=2cm,△ADE的周长为4cm,则△ABC的周长是 cm.
三.解答题(共5小题)
21.(2014秋 临洮县校级月考)如图示,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA=12,则△PEF的周长是?
22.(2014秋 琼海校级期中)如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
23.(2014秋 张家港市期末)如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E;
(1)求证:BE=CE;
(2)若以O、D、E、C为顶点的四边形是正方形,⊙O的半径为r,求△ABC的面积;
(3)若EC=4,BD=,求⊙O的半径OC的长.
24.(2015 潍坊模拟)如图,PA、PB切⊙O于A、B,若∠APB=60°,⊙O半径为3,求阴影部分面积.
25.(2014秋 仙游县期中)已知:AB为⊙O的直径,∠A=∠B=90°,DE与⊙O相切于E,⊙O的半径为,AD=2.
①求BC的长;
②延长AE交BC的延长线于G点,求EG的长.
鲁教版九年级数学下册第5章5.7切线长定理同步训练题参考答案
一.选择题(共10小题)
1.B 2.D 3.B 4.D 5.C 6.A 7.B 8.C 9.B 10.A
二.填空题(共10小题)
11.52 12. 13.11 14.6 15.2 16.7 17.5
18.6:7 19.12 20.8
三.解答题(共5小题)
21.解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在弧AB上,
∴AE=CE,FB=CF,PA=PB=12,
∴△PEF的周长=PE+EF+PF=PA+PB=24.
22.解:(1)∵PA,PB是⊙O的切线,∴AP=BP,
∵∠P=60°,∴∠PAB=60°,
∵AC是⊙O的直径,∴∠PAC=90°,∴∠BAC=90°﹣60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
∴OP=4,
由勾股定理得:,
∵AP=BP,∠APB=60°,
∴△APB是等边三角形,
∴.
23.(1)证明:连接CD,由AC是直径知CD⊥AB;
DE、CE都是切线,所以DE=CE,∠EDC=∠ECD;
又∠B+∠ECD=90°,∠BDE+∠EDC=90°;
所以∠B=∠BDE,所以BE=DE,从而BE=CE;
(2)解:连接OD,
当以O、D、E、C为顶点的四边形是正方形时,DE=EC=OC=OD=r;
从而BE=r,即△ABC是一个等腰直角三角形;
AC=AB=2r,S△ABC=2r2;
(3)解:若EC=4,BD=4,则BC=8;
在Rt△BDC中,cos∠CBD==;所以∠CBD=30°;
在Rt△ABC中,=tan30°,即AC=BCtan30°=8×=,OC==;
另解:设OC=r,AD=x;由EC=4,BD=4得BC=8,DC=4;
则:,解得;即OC=.
(23题图) (24题图) (25题图)
24.解:连接PO与AO,
∵PA、PB切⊙O于A、B,若∠APB=60°,∴OA⊥PA,∠APO=∠APB=30°,
∴∠AOP=60°,
∵⊙O半径为3,∴OA=3,PO=6,∴PA==3,
∴S△PAO=AO PA=×3×3=,S扇形AOC==π,
∴S阴影=2×(S△PAO﹣S扇形AOC)=2×(﹣π)=9﹣3π.
∴阴影部分面积为:9﹣3π.
25.解:①过点D作DF⊥BC于点F,
∵AB为⊙O的直径,∠A=∠B=90°,
∴四边形ABFD是矩形,AD与BC是⊙O的切线,
∴DF=AB=2,BF=AD=2,
∵DE与⊙O相切,
∴DE=AD=2,CE=BC,
设BC=x,则CF=BC﹣BF=x﹣2,DC=DE+CE=2+x,
在Rt△DCF中,DC2=CF2+DF2,即(2+x)2=(x﹣2)2+(2)2,解得:x=,
即BC=;
②∵AB为⊙O的直径,∠A=∠B=90°,∴AD∥BC,∴△ADE∽△GCE,
∴AD:CG=DE:CE,AE:EG=AD:CG,
∵AD=DE=2,∴CG=CE=BC=,∴BG=BC+CG=5,∴AE:EG=4:5,
在Rt△ABG中,AG==3,∴EG=AG=.
