福建省厦门市第十一中学2023-2024学年九年级上学期数学开学考试模拟试卷(含答案)
文档属性
| 名称 | 福建省厦门市第十一中学2023-2024学年九年级上学期数学开学考试模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 199.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 17:46:15 | ||
图片预览



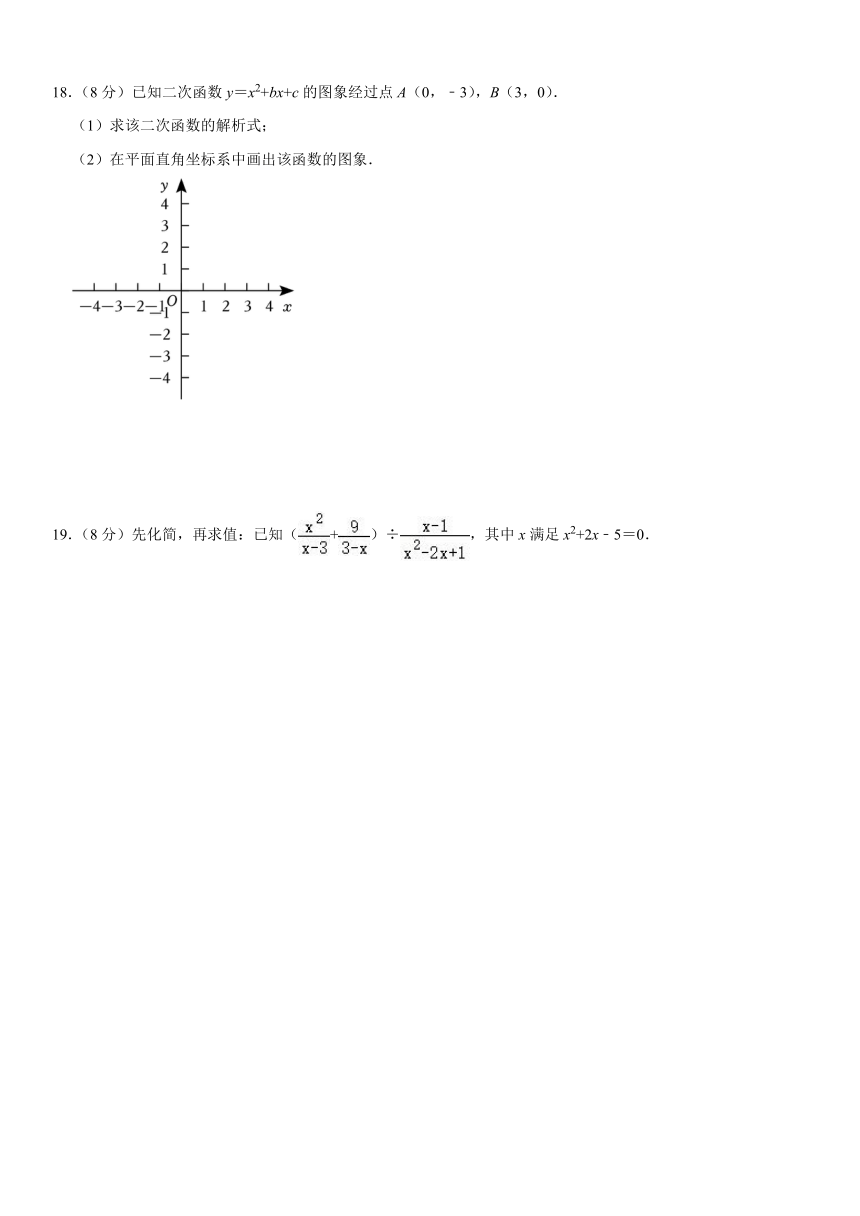

文档简介
福建省厦门市第十一中学2023-2024学年九年级上学期开学考试模拟试卷
一.选择题(共10小题,满分40分,每小题4分)
1.(4分)一元二次方程2x2﹣x+1=0的二次项系数是( )
A.2 B.1 C.0 D.﹣1
2.(4分)若二次根式有意义,则x的值不可以是( )
A.3 B.2 C.1 D.0
3.(4分)已知某二次函数,当x>1时,y随x的增大而减小;当x<1时,y随x的增大而增大,则该二次函数的解析式可以是( )
A.y=3(x+1)2 B.y=3(x﹣1)2
C.y=﹣3(x+1)2 D.y=﹣3(x﹣1)2
4.(4分)对一组数据:4、6、﹣4、6、8,描述正确的是( )
A.中位数是﹣4 B.平均数是5
C.众数是6 D.方差是7
5.(4分)如何将二次函数平移得到二次函数,下列选项正确的是( )
A.向左平移1个单位,再向上平移1个单位
B.向左平移1个单位,再向下平移1个单位
C.向右平移1个单位,再向上平移1个单位
D.向右平移1个单位,再向下平移1个单位
6.(4分)某学校连续三年组织学生向山区捐送图书,第一年共捐书400本,三年共捐书1525本.设该校捐书本数的年平均增长率为x,根据题意,下列方程正确的是( )
A.1525(1﹣x)2=400
B.400(1+x)2=1525
C.400+400(1+x)+400(1+x)2=1525
D.400x2=1525
7.(4分)如图,在平面直角坐标系中,点A在y轴上,点B的坐标为(4,0),将△ABO绕着点B顺时针旋转60°,得到△DBC,则点C的坐标是( )
A. B. C.(4,2) D.(2,4)
8.(4分)平行四边形ABCD中,AB=5,BC=3,若一边上的高为4,则该平行四边形的面积为( )
A.20 B.16 C.15 D.12
9.(4分)已知点P(m2,n),点Q(2m﹣3,n),下列关于点P与点Q的位置关系说法正确的是( )
A.点P在点Q的右边
B.点P在点Q的左边
C.点P与点Q有可能重合
D.点P与点Q的位置关系无法确定
10.(4分)已知a,b,c分别是Rt△ABC的三条边长,c为斜边长,∠C=90°,我们把关于x的形如y=x+的一次函数称为“勾股一次函数”,若点P(﹣1,)在“勾股一次函数”的图象上,且Rt△ABC的面积是2,则c的值是( )
A.3 B.4 C.5 D.6
二.填空题(共6小题,满分24分,每小题4分)
11.(4分)已知一次函数y=2x+(k﹣3)的图象经过第一、三、四象限,那么k的取值范围为 .
12.(4分)某组数据的方差计算公式为S2=[(x1﹣2)2+(x2﹣2)2+(x3﹣2)2+(x4﹣2)2+(x5﹣2)2],则这组数据的平均数是 .
13.(4分)如果关于x的方程kx2+3x﹣1=0有两个不相等的实数根,那么k的取值范围是 .
14.(4分)如图所示为函数y=x2+bx﹣1的图象,根据图象提供的信息,当﹣1≤x≤4时,y的取值范围是 .
15.(4分)如图,Rt△ABC的周长为24,∠C=90°,且AB:AC=5:4,则BC的长为 .
16.(4分)如图,在菱形ABCD中,AB=6,∠D=60°.点P为边CD上一点,且不与点C,D重合,连接BP,过点A作EF∥BP,且EF=BP,连接BE,PF,则四边形BEFP的面积为 .
三.解答题(共9小题,满分86分)
17.(8分)(1)计算:. (2)解方程 x2﹣4x+1=0.
18.(8分)已知二次函数y=x2+bx+c的图象经过点A(0,﹣3),B(3,0).
(1)求该二次函数的解析式;
(2)在平面直角坐标系中画出该函数的图象.
19.(8分)先化简,再求值:已知(+)÷,其中x满足x2+2x﹣5=0.
20.(8分)某中学在一次爱心捐款活动中,全体同学积极踊跃捐款.现随机抽查了八年级20位同学捐款情况,并绘制出统计表和统计图.根据上述信息,回答下列问题:
捐款(元) 20 50 100 150 200
人数(人) 4 8 n 2 1
(1)m= ,n= ;
(2)学生捐款数目的众数是 元,中位数是 元,平均数是 元;
(3)若该校有学生1500人,估计该校学生共捐款多少元?
21.(8分)如图,在△ABC中,D,E分别是边AB,AC的中点.
(1)求作:平行四边形ADCF(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)所作的图形中,若DE=3,AB=10,AC=8,求证:四边形ADCF是菱形.
22.(10分)已知m、n分别是关于x的一元二次方程ax2+bx+c=a与ax2+bx+c=b的一个根,且m=n+1.
(1)当m=2,a=﹣1时,求b与c的值;
(2)用只含字母a、n的代数式表示b;
(3)当a<0时,函数y=ax2+bx+c满足b2﹣4ca=a,b+c≥2a,n≤,求a的取值范围.
23.(10分)为充分利用现有资源,学校“牧春园”计划用一块矩形地种植两种花卉.如图,矩形地ABCD一面靠墙(墙的长度为12m),另外三面用栅栏围成,中间再用栅栏EF把它分成两个面积相等的矩形.已知栅栏的总长度为27m.
(1)若矩形地ABCD的面积为42m2,求AB的长;
(2)当AB边为多少时,矩形地ABCD的面积最大,最大面积是多少?
24.(12分)根据以下素材,探索完成任务.
如何设计警戒线之间的宽度
素材1 图1为某公园的抛物线型拱桥,图2是其横截面示意图,测得水面宽度AB=24米,拱顶离水面的距离为CD=4米.
素材2 拟在公园里投放游船供游客乘坐,载重最少时,游船的横截面如图3所示,漏出水面的船身为矩形,船顶为等腰三角形.如图3,测得相关数据如下:EF=EK=1.7米,FK=3米,GH=IJ=1.26米,FG=JK=0.4米.
素材3 为确保安全,拟在石拱桥下面的P,Q两处设置航行警戒线,要求如下: ①游船底部HI在P,Q之间通行; ②当载重最少通过时,游船顶部E与拱桥的竖直距离至少为0.25米.
问题解决
任务1 确定拱桥形状 在图2中建立合适的直角坐标系,并求这条抛物线的解析式;
任务2 设计警戒线之间的宽度 求PQ的最大值.
25.(14分)已知抛物线y=﹣﹣2x+3n(n>0)与x轴交于A,B两点(点A位于点B的左侧);与y轴交于点C,顶点为D.
(1)如图1,若n=1.
①则D的坐标为 ;
②当m≤x≤0时,抛物线的最小值为3,最大值为4,则m的取值范围为 .
(2)如图2,P是抛物线上一点,Q为射线CA上一点,且P、Q两点均在第三象限内,Q、A是位于直线PB同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2nd.
①求证:AC∥PB.
②连接AP、OD、OQ、DQ,若AP=QB,PQ=4n,试判断△DOQ的形状是否随着n的变化而变化?并说明理由.
福建省厦门市第十一中学2023-2024学年九年级上学期开学考试模拟试卷(答案)
一.选择题(共10小题,满分40分,每小题4分)
1.(4分)一元二次方程2x2﹣x+1=0的二次项系数是( )
A.2 B.1 C.0 D.﹣1
【答案】A
2.(4分)若二次根式有意义,则x的值不可以是( )
A.3 B.2 C.1 D.0
【答案】A
3.(4分)已知某二次函数,当x>1时,y随x的增大而减小;当x<1时,y随x的增大而增大,则该二次函数的解析式可以是( )
A.y=3(x+1)2 B.y=3(x﹣1)2
C.y=﹣3(x+1)2 D.y=﹣3(x﹣1)2
【答案】D
4.(4分)对一组数据:4、6、﹣4、6、8,描述正确的是( )
A.中位数是﹣4 B.平均数是5
C.众数是6 D.方差是7
【答案】C
5.(4分)如何将二次函数平移得到二次函数,下列选项正确的是( )
A.向左平移1个单位,再向上平移1个单位
B.向左平移1个单位,再向下平移1个单位
C.向右平移1个单位,再向上平移1个单位
D.向右平移1个单位,再向下平移1个单位
【答案】B
6.(4分)某学校连续三年组织学生向山区捐送图书,第一年共捐书400本,三年共捐书1525本.设该校捐书本数的年平均增长率为x,根据题意,下列方程正确的是( )
A.1525(1﹣x)2=400
B.400(1+x)2=1525
C.400+400(1+x)+400(1+x)2=1525
D.400x2=1525
【答案】C
7.(4分)如图,在平面直角坐标系中,点A在y轴上,点B的坐标为(4,0),将△ABO绕着点B顺时针旋转60°,得到△DBC,则点C的坐标是( )
A. B. C.(4,2) D.(2,4)
【答案】B
8.(4分)平行四边形ABCD中,AB=5,BC=3,若一边上的高为4,则该平行四边形的面积为( )
A.20 B.16 C.15 D.12
【答案】D
9.(4分)已知点P(m2,n),点Q(2m﹣3,n),下列关于点P与点Q的位置关系说法正确的是( )
A.点P在点Q的右边
B.点P在点Q的左边
C.点P与点Q有可能重合
D.点P与点Q的位置关系无法确定
【答案】A
10.(4分)已知a,b,c分别是Rt△ABC的三条边长,c为斜边长,∠C=90°,我们把关于x的形如y=x+的一次函数称为“勾股一次函数”,若点P(﹣1,)在“勾股一次函数”的图象上,且Rt△ABC的面积是2,则c的值是( )
A.3 B.4 C.5 D.6
【答案】A
二.填空题(共6小题,满分24分,每小题4分)
11.(4分)已知一次函数y=2x+(k﹣3)的图象经过第一、三、四象限,那么k的取值范围为 k<3 .
【答案】k<3.
12.(4分)某组数据的方差计算公式为S2=[(x1﹣2)2+(x2﹣2)2+(x3﹣2)2+(x4﹣2)2+(x5﹣2)2],则这组数据的平均数是 2 .
【答案】2.
13.(4分)如果关于x的方程kx2+3x﹣1=0有两个不相等的实数根,那么k的取值范围是 k>﹣且k≠0 .
【答案】k>﹣且k≠0.
14.(4分)如图所示为函数y=x2+bx﹣1的图象,根据图象提供的信息,当﹣1≤x≤4时,y的取值范围是 ﹣2≤y≤7 .
【答案】﹣2≤y≤7.
15.(4分)如图,Rt△ABC的周长为24,∠C=90°,且AB:AC=5:4,则BC的长为 6 .
【答案】6.
16.(4分)如图,在菱形ABCD中,AB=6,∠D=60°.点P为边CD上一点,且不与点C,D重合,连接BP,过点A作EF∥BP,且EF=BP,连接BE,PF,则四边形BEFP的面积为 18 .
【答案】18.
三.解答题(共9小题,满分86分)
17.(8分)(1)计算:.
(2)解方程 x2﹣4x+1=0.
【答案】(1)﹣1+4;
(2)x1=2+,x2=2﹣.
18.(8分)已知二次函数y=x2+bx+c的图象经过点A(0,﹣3),B(3,0).
(1)求该二次函数的解析式;
(2)在平面直角坐标系中画出该函数的图象.
【答案】(1)y=x2﹣2x﹣3;(2)见解析.
19.(8分)先化简,再求值:已知(+)÷,其中x满足x2+2x﹣5=0.
【答案】x2+2x﹣3,2.
20.(8分)某中学在一次爱心捐款活动中,全体同学积极踊跃捐款.现随机抽查了八年级20位同学捐款情况,并绘制出统计表和统计图.根据上述信息,回答下列问题:
捐款(元) 20 50 100 150 200
人数(人) 4 8 n 2 1
(1)m= 40 ,n= 5 ;
(2)学生捐款数目的众数是 50 元,中位数是 50 元,平均数是 74 元;
(3)若该校有学生1500人,估计该校学生共捐款多少元?
【答案】(1)40,5;(2)50,50,74;(3)111000元.
21.(8分)如图,在△ABC中,D,E分别是边AB,AC的中点.
(1)求作:平行四边形ADCF(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)所作的图形中,若DE=3,AB=10,AC=8,求证:四边形ADCF是菱形.
【答案】(1)作图见解答过程;
(2)证明见解答过程.
22.(10分)已知m、n分别是关于x的一元二次方程ax2+bx+c=a与ax2+bx+c=b的一个根,且m=n+1.
(1)当m=2,a=﹣1时,求b与c的值;
(2)用只含字母a、n的代数式表示b;
(3)当a<0时,函数y=ax2+bx+c满足b2﹣4ca=a,b+c≥2a,n≤,求a的取值范围.
【答案】(1)b=1,c=1;
(2)b=﹣an;
(3)a≤﹣.
23.(10分)为充分利用现有资源,学校“牧春园”计划用一块矩形地种植两种花卉.如图,矩形地ABCD一面靠墙(墙的长度为12m),另外三面用栅栏围成,中间再用栅栏EF把它分成两个面积相等的矩形.已知栅栏的总长度为27m.
(1)若矩形地ABCD的面积为42m2,求AB的长;
(2)当AB边为多少时,矩形地ABCD的面积最大,最大面积是多少?
【答案】(1)AB的长为7m;
(2)当AB边为5时,矩形地ABCD的面积最大,最大面积是60m2.
24.(12分)根据以下素材,探索完成任务.
如何设计警戒线之间的宽度
素材1 图1为某公园的抛物线型拱桥,图2是其横截面示意图,测得水面宽度AB=24米,拱顶离水面的距离为CD=4米.
素材2 拟在公园里投放游船供游客乘坐,载重最少时,游船的横截面如图3所示,漏出水面的船身为矩形,船顶为等腰三角形.如图3,测得相关数据如下:EF=EK=1.7米,FK=3米,GH=IJ=1.26米,FG=JK=0.4米.
素材3 为确保安全,拟在石拱桥下面的P,Q两处设置航行警戒线,要求如下: ①游船底部HI在P,Q之间通行; ②当载重最少通过时,游船顶部E与拱桥的竖直距离至少为0.25米.
问题解决
任务1 确定拱桥形状 在图2中建立合适的直角坐标系,并求这条抛物线的解析式;
任务2 设计警戒线之间的宽度 求PQ的最大值.
【答案】【任务1】,
【任务2】17.8.
25.(14分)已知抛物线y=﹣﹣2x+3n(n>0)与x轴交于A,B两点(点A位于点B的左侧);与y轴交于点C,顶点为D.
(1)如图1,若n=1.
①则D的坐标为 (﹣1,4) ;
②当m≤x≤0时,抛物线的最小值为3,最大值为4,则m的取值范围为 ﹣2≤m≤﹣1 .
(2)如图2,P是抛物线上一点,Q为射线CA上一点,且P、Q两点均在第三象限内,Q、A是位于直线PB同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2nd.
①求证:AC∥PB.
②连接AP、OD、OQ、DQ,若AP=QB,PQ=4n,试判断△DOQ的形状是否随着n的变化而变化?并说明理由.
【答案】(1)①(﹣1,4);
②﹣2≤m≤﹣1;
(2)②△DOQ的形状不会随着n的变化而变化.
一.选择题(共10小题,满分40分,每小题4分)
1.(4分)一元二次方程2x2﹣x+1=0的二次项系数是( )
A.2 B.1 C.0 D.﹣1
2.(4分)若二次根式有意义,则x的值不可以是( )
A.3 B.2 C.1 D.0
3.(4分)已知某二次函数,当x>1时,y随x的增大而减小;当x<1时,y随x的增大而增大,则该二次函数的解析式可以是( )
A.y=3(x+1)2 B.y=3(x﹣1)2
C.y=﹣3(x+1)2 D.y=﹣3(x﹣1)2
4.(4分)对一组数据:4、6、﹣4、6、8,描述正确的是( )
A.中位数是﹣4 B.平均数是5
C.众数是6 D.方差是7
5.(4分)如何将二次函数平移得到二次函数,下列选项正确的是( )
A.向左平移1个单位,再向上平移1个单位
B.向左平移1个单位,再向下平移1个单位
C.向右平移1个单位,再向上平移1个单位
D.向右平移1个单位,再向下平移1个单位
6.(4分)某学校连续三年组织学生向山区捐送图书,第一年共捐书400本,三年共捐书1525本.设该校捐书本数的年平均增长率为x,根据题意,下列方程正确的是( )
A.1525(1﹣x)2=400
B.400(1+x)2=1525
C.400+400(1+x)+400(1+x)2=1525
D.400x2=1525
7.(4分)如图,在平面直角坐标系中,点A在y轴上,点B的坐标为(4,0),将△ABO绕着点B顺时针旋转60°,得到△DBC,则点C的坐标是( )
A. B. C.(4,2) D.(2,4)
8.(4分)平行四边形ABCD中,AB=5,BC=3,若一边上的高为4,则该平行四边形的面积为( )
A.20 B.16 C.15 D.12
9.(4分)已知点P(m2,n),点Q(2m﹣3,n),下列关于点P与点Q的位置关系说法正确的是( )
A.点P在点Q的右边
B.点P在点Q的左边
C.点P与点Q有可能重合
D.点P与点Q的位置关系无法确定
10.(4分)已知a,b,c分别是Rt△ABC的三条边长,c为斜边长,∠C=90°,我们把关于x的形如y=x+的一次函数称为“勾股一次函数”,若点P(﹣1,)在“勾股一次函数”的图象上,且Rt△ABC的面积是2,则c的值是( )
A.3 B.4 C.5 D.6
二.填空题(共6小题,满分24分,每小题4分)
11.(4分)已知一次函数y=2x+(k﹣3)的图象经过第一、三、四象限,那么k的取值范围为 .
12.(4分)某组数据的方差计算公式为S2=[(x1﹣2)2+(x2﹣2)2+(x3﹣2)2+(x4﹣2)2+(x5﹣2)2],则这组数据的平均数是 .
13.(4分)如果关于x的方程kx2+3x﹣1=0有两个不相等的实数根,那么k的取值范围是 .
14.(4分)如图所示为函数y=x2+bx﹣1的图象,根据图象提供的信息,当﹣1≤x≤4时,y的取值范围是 .
15.(4分)如图,Rt△ABC的周长为24,∠C=90°,且AB:AC=5:4,则BC的长为 .
16.(4分)如图,在菱形ABCD中,AB=6,∠D=60°.点P为边CD上一点,且不与点C,D重合,连接BP,过点A作EF∥BP,且EF=BP,连接BE,PF,则四边形BEFP的面积为 .
三.解答题(共9小题,满分86分)
17.(8分)(1)计算:. (2)解方程 x2﹣4x+1=0.
18.(8分)已知二次函数y=x2+bx+c的图象经过点A(0,﹣3),B(3,0).
(1)求该二次函数的解析式;
(2)在平面直角坐标系中画出该函数的图象.
19.(8分)先化简,再求值:已知(+)÷,其中x满足x2+2x﹣5=0.
20.(8分)某中学在一次爱心捐款活动中,全体同学积极踊跃捐款.现随机抽查了八年级20位同学捐款情况,并绘制出统计表和统计图.根据上述信息,回答下列问题:
捐款(元) 20 50 100 150 200
人数(人) 4 8 n 2 1
(1)m= ,n= ;
(2)学生捐款数目的众数是 元,中位数是 元,平均数是 元;
(3)若该校有学生1500人,估计该校学生共捐款多少元?
21.(8分)如图,在△ABC中,D,E分别是边AB,AC的中点.
(1)求作:平行四边形ADCF(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)所作的图形中,若DE=3,AB=10,AC=8,求证:四边形ADCF是菱形.
22.(10分)已知m、n分别是关于x的一元二次方程ax2+bx+c=a与ax2+bx+c=b的一个根,且m=n+1.
(1)当m=2,a=﹣1时,求b与c的值;
(2)用只含字母a、n的代数式表示b;
(3)当a<0时,函数y=ax2+bx+c满足b2﹣4ca=a,b+c≥2a,n≤,求a的取值范围.
23.(10分)为充分利用现有资源,学校“牧春园”计划用一块矩形地种植两种花卉.如图,矩形地ABCD一面靠墙(墙的长度为12m),另外三面用栅栏围成,中间再用栅栏EF把它分成两个面积相等的矩形.已知栅栏的总长度为27m.
(1)若矩形地ABCD的面积为42m2,求AB的长;
(2)当AB边为多少时,矩形地ABCD的面积最大,最大面积是多少?
24.(12分)根据以下素材,探索完成任务.
如何设计警戒线之间的宽度
素材1 图1为某公园的抛物线型拱桥,图2是其横截面示意图,测得水面宽度AB=24米,拱顶离水面的距离为CD=4米.
素材2 拟在公园里投放游船供游客乘坐,载重最少时,游船的横截面如图3所示,漏出水面的船身为矩形,船顶为等腰三角形.如图3,测得相关数据如下:EF=EK=1.7米,FK=3米,GH=IJ=1.26米,FG=JK=0.4米.
素材3 为确保安全,拟在石拱桥下面的P,Q两处设置航行警戒线,要求如下: ①游船底部HI在P,Q之间通行; ②当载重最少通过时,游船顶部E与拱桥的竖直距离至少为0.25米.
问题解决
任务1 确定拱桥形状 在图2中建立合适的直角坐标系,并求这条抛物线的解析式;
任务2 设计警戒线之间的宽度 求PQ的最大值.
25.(14分)已知抛物线y=﹣﹣2x+3n(n>0)与x轴交于A,B两点(点A位于点B的左侧);与y轴交于点C,顶点为D.
(1)如图1,若n=1.
①则D的坐标为 ;
②当m≤x≤0时,抛物线的最小值为3,最大值为4,则m的取值范围为 .
(2)如图2,P是抛物线上一点,Q为射线CA上一点,且P、Q两点均在第三象限内,Q、A是位于直线PB同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2nd.
①求证:AC∥PB.
②连接AP、OD、OQ、DQ,若AP=QB,PQ=4n,试判断△DOQ的形状是否随着n的变化而变化?并说明理由.
福建省厦门市第十一中学2023-2024学年九年级上学期开学考试模拟试卷(答案)
一.选择题(共10小题,满分40分,每小题4分)
1.(4分)一元二次方程2x2﹣x+1=0的二次项系数是( )
A.2 B.1 C.0 D.﹣1
【答案】A
2.(4分)若二次根式有意义,则x的值不可以是( )
A.3 B.2 C.1 D.0
【答案】A
3.(4分)已知某二次函数,当x>1时,y随x的增大而减小;当x<1时,y随x的增大而增大,则该二次函数的解析式可以是( )
A.y=3(x+1)2 B.y=3(x﹣1)2
C.y=﹣3(x+1)2 D.y=﹣3(x﹣1)2
【答案】D
4.(4分)对一组数据:4、6、﹣4、6、8,描述正确的是( )
A.中位数是﹣4 B.平均数是5
C.众数是6 D.方差是7
【答案】C
5.(4分)如何将二次函数平移得到二次函数,下列选项正确的是( )
A.向左平移1个单位,再向上平移1个单位
B.向左平移1个单位,再向下平移1个单位
C.向右平移1个单位,再向上平移1个单位
D.向右平移1个单位,再向下平移1个单位
【答案】B
6.(4分)某学校连续三年组织学生向山区捐送图书,第一年共捐书400本,三年共捐书1525本.设该校捐书本数的年平均增长率为x,根据题意,下列方程正确的是( )
A.1525(1﹣x)2=400
B.400(1+x)2=1525
C.400+400(1+x)+400(1+x)2=1525
D.400x2=1525
【答案】C
7.(4分)如图,在平面直角坐标系中,点A在y轴上,点B的坐标为(4,0),将△ABO绕着点B顺时针旋转60°,得到△DBC,则点C的坐标是( )
A. B. C.(4,2) D.(2,4)
【答案】B
8.(4分)平行四边形ABCD中,AB=5,BC=3,若一边上的高为4,则该平行四边形的面积为( )
A.20 B.16 C.15 D.12
【答案】D
9.(4分)已知点P(m2,n),点Q(2m﹣3,n),下列关于点P与点Q的位置关系说法正确的是( )
A.点P在点Q的右边
B.点P在点Q的左边
C.点P与点Q有可能重合
D.点P与点Q的位置关系无法确定
【答案】A
10.(4分)已知a,b,c分别是Rt△ABC的三条边长,c为斜边长,∠C=90°,我们把关于x的形如y=x+的一次函数称为“勾股一次函数”,若点P(﹣1,)在“勾股一次函数”的图象上,且Rt△ABC的面积是2,则c的值是( )
A.3 B.4 C.5 D.6
【答案】A
二.填空题(共6小题,满分24分,每小题4分)
11.(4分)已知一次函数y=2x+(k﹣3)的图象经过第一、三、四象限,那么k的取值范围为 k<3 .
【答案】k<3.
12.(4分)某组数据的方差计算公式为S2=[(x1﹣2)2+(x2﹣2)2+(x3﹣2)2+(x4﹣2)2+(x5﹣2)2],则这组数据的平均数是 2 .
【答案】2.
13.(4分)如果关于x的方程kx2+3x﹣1=0有两个不相等的实数根,那么k的取值范围是 k>﹣且k≠0 .
【答案】k>﹣且k≠0.
14.(4分)如图所示为函数y=x2+bx﹣1的图象,根据图象提供的信息,当﹣1≤x≤4时,y的取值范围是 ﹣2≤y≤7 .
【答案】﹣2≤y≤7.
15.(4分)如图,Rt△ABC的周长为24,∠C=90°,且AB:AC=5:4,则BC的长为 6 .
【答案】6.
16.(4分)如图,在菱形ABCD中,AB=6,∠D=60°.点P为边CD上一点,且不与点C,D重合,连接BP,过点A作EF∥BP,且EF=BP,连接BE,PF,则四边形BEFP的面积为 18 .
【答案】18.
三.解答题(共9小题,满分86分)
17.(8分)(1)计算:.
(2)解方程 x2﹣4x+1=0.
【答案】(1)﹣1+4;
(2)x1=2+,x2=2﹣.
18.(8分)已知二次函数y=x2+bx+c的图象经过点A(0,﹣3),B(3,0).
(1)求该二次函数的解析式;
(2)在平面直角坐标系中画出该函数的图象.
【答案】(1)y=x2﹣2x﹣3;(2)见解析.
19.(8分)先化简,再求值:已知(+)÷,其中x满足x2+2x﹣5=0.
【答案】x2+2x﹣3,2.
20.(8分)某中学在一次爱心捐款活动中,全体同学积极踊跃捐款.现随机抽查了八年级20位同学捐款情况,并绘制出统计表和统计图.根据上述信息,回答下列问题:
捐款(元) 20 50 100 150 200
人数(人) 4 8 n 2 1
(1)m= 40 ,n= 5 ;
(2)学生捐款数目的众数是 50 元,中位数是 50 元,平均数是 74 元;
(3)若该校有学生1500人,估计该校学生共捐款多少元?
【答案】(1)40,5;(2)50,50,74;(3)111000元.
21.(8分)如图,在△ABC中,D,E分别是边AB,AC的中点.
(1)求作:平行四边形ADCF(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)所作的图形中,若DE=3,AB=10,AC=8,求证:四边形ADCF是菱形.
【答案】(1)作图见解答过程;
(2)证明见解答过程.
22.(10分)已知m、n分别是关于x的一元二次方程ax2+bx+c=a与ax2+bx+c=b的一个根,且m=n+1.
(1)当m=2,a=﹣1时,求b与c的值;
(2)用只含字母a、n的代数式表示b;
(3)当a<0时,函数y=ax2+bx+c满足b2﹣4ca=a,b+c≥2a,n≤,求a的取值范围.
【答案】(1)b=1,c=1;
(2)b=﹣an;
(3)a≤﹣.
23.(10分)为充分利用现有资源,学校“牧春园”计划用一块矩形地种植两种花卉.如图,矩形地ABCD一面靠墙(墙的长度为12m),另外三面用栅栏围成,中间再用栅栏EF把它分成两个面积相等的矩形.已知栅栏的总长度为27m.
(1)若矩形地ABCD的面积为42m2,求AB的长;
(2)当AB边为多少时,矩形地ABCD的面积最大,最大面积是多少?
【答案】(1)AB的长为7m;
(2)当AB边为5时,矩形地ABCD的面积最大,最大面积是60m2.
24.(12分)根据以下素材,探索完成任务.
如何设计警戒线之间的宽度
素材1 图1为某公园的抛物线型拱桥,图2是其横截面示意图,测得水面宽度AB=24米,拱顶离水面的距离为CD=4米.
素材2 拟在公园里投放游船供游客乘坐,载重最少时,游船的横截面如图3所示,漏出水面的船身为矩形,船顶为等腰三角形.如图3,测得相关数据如下:EF=EK=1.7米,FK=3米,GH=IJ=1.26米,FG=JK=0.4米.
素材3 为确保安全,拟在石拱桥下面的P,Q两处设置航行警戒线,要求如下: ①游船底部HI在P,Q之间通行; ②当载重最少通过时,游船顶部E与拱桥的竖直距离至少为0.25米.
问题解决
任务1 确定拱桥形状 在图2中建立合适的直角坐标系,并求这条抛物线的解析式;
任务2 设计警戒线之间的宽度 求PQ的最大值.
【答案】【任务1】,
【任务2】17.8.
25.(14分)已知抛物线y=﹣﹣2x+3n(n>0)与x轴交于A,B两点(点A位于点B的左侧);与y轴交于点C,顶点为D.
(1)如图1,若n=1.
①则D的坐标为 (﹣1,4) ;
②当m≤x≤0时,抛物线的最小值为3,最大值为4,则m的取值范围为 ﹣2≤m≤﹣1 .
(2)如图2,P是抛物线上一点,Q为射线CA上一点,且P、Q两点均在第三象限内,Q、A是位于直线PB同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2nd.
①求证:AC∥PB.
②连接AP、OD、OQ、DQ,若AP=QB,PQ=4n,试判断△DOQ的形状是否随着n的变化而变化?并说明理由.
【答案】(1)①(﹣1,4);
②﹣2≤m≤﹣1;
(2)②△DOQ的形状不会随着n的变化而变化.
同课章节目录
