【大单元教学】小学数学六下 2.3 圆柱的体积 教案(苏教版)
文档属性
| 名称 | 【大单元教学】小学数学六下 2.3 圆柱的体积 教案(苏教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 700.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 17:52:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
《圆柱和圆锥》单元整体教学设计
单元名称 苏教版六年级下册第二单元:《圆柱和圆锥》
课程标准分析 《圆柱与圆锥》单元是图形与几何领域第三学段“图形与几何”中的重要内容。《课程标准》在“内容要求”提出了: 1.通过实例了解圆柱、圆锥体积 (或容积)的意义,知道圆柱、圆锥体积(或容积)的度量单位,能进行单位之间的换算;体验不规则物体体积的测量方法 2.认识圆柱和圆锥,了解圆柱的展开图,探索并掌握圆柱的体积和表面积的计算公式,探索圆锥体积的计算公式,能用这些公式解决生活中的实际问题。 《课程标准》在“学业要求”中指出:认识圆柱和圆锥,能说出圆柱和圆锥的特征,能辨认这些圆柱的展开图,会计算圆柱的体积和表面积;会计算圆锥的体积;能用相应公式解决生活中实际问题。
内容分析 圆柱和圆锥都是平面与曲面围成的立体图形,是在圆的知识与长方体、正方体知识的基础上编排的,通过认识圆柱和圆锥的特征,理解圆柱侧面积和表面积的含义及计算方法,探索并应用圆柱和圆锥的体积计算公式,进一步发展空间观念和思维能力。
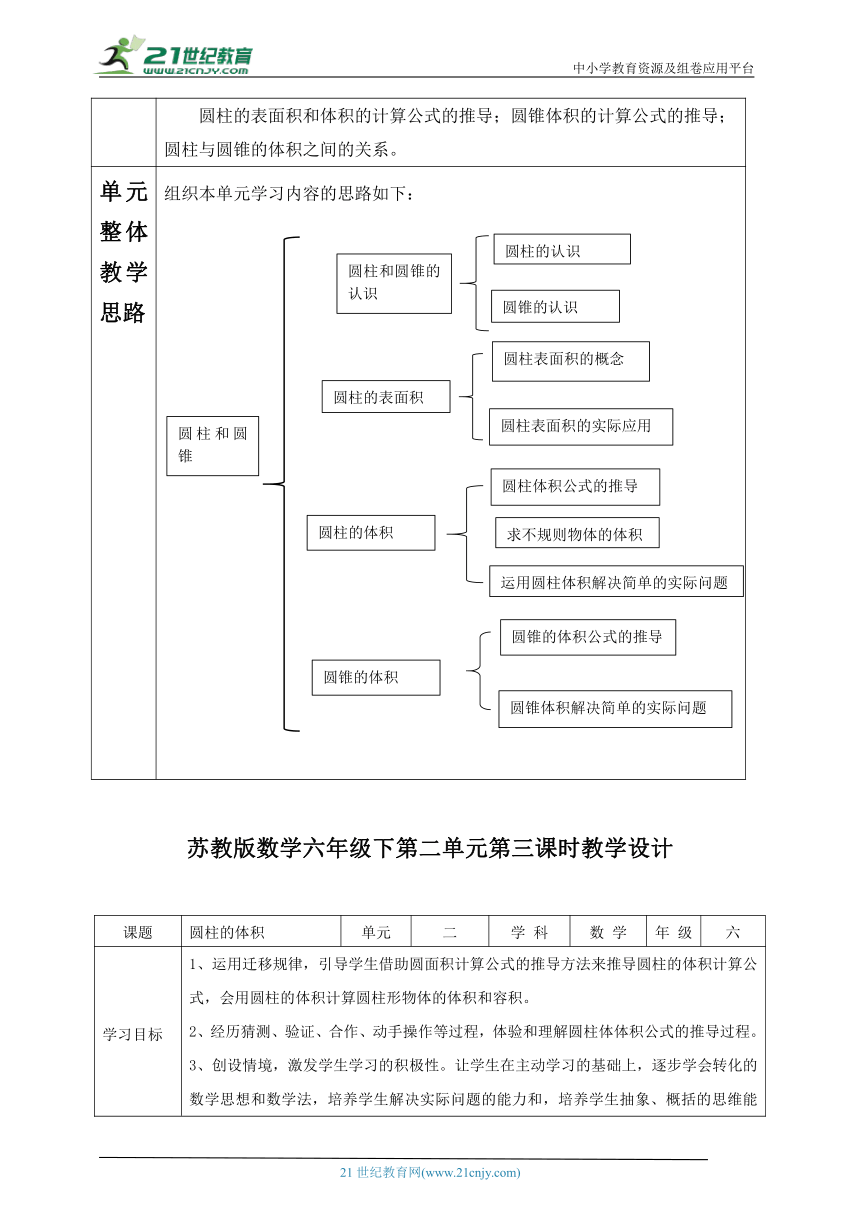
单元目标 一、单元目标拟定 1.认识圆柱和圆锥,掌握其特征和几个部分的名称与特点,建立几何模型。 2.认识圆柱的侧面及其展开图,并掌握侧面展开的长方形与圆柱相对应部分的关系。 3.熟练掌握圆柱表面积、圆柱体积、圆锥体积的计算公式,理解圆柱表面积、圆柱、体积、圆锥体积的知识在日常生活中的应用。感受数学知识与实际生活的密切联系,体会学习数学的乐趣。 二、关键内容确定 (一)教学重点 圆柱的表面积、体积的计算;圆锥体积的计算。 (二)教学难点 圆柱的表面积和体积的计算公式的推导;圆锥体积的计算公式的推导;圆柱与圆锥的体积之间的关系。
单元整体教学思路 组织本单元学习内容的思路如下:
苏教版数学六年级下第二单元第三课时教学设计
课题 圆柱的体积 单元 二 学 科 数 学 年 级 六
学习目标 1、运用迁移规律,引导学生借助圆面积计算公式的推导方法来推导圆柱的体积计算公式,会用圆柱的体积计算圆柱形物体的体积和容积。 2、经历猜测、验证、合作、动手操作等过程,体验和理解圆柱体体积公式的推导过程。 3、创设情境,激发学生学习的积极性。让学生在主动学习的基础上,逐步学会转化的数学思想和数学法,培养学生解决实际问题的能力和,培养学生抽象、概括的思维能力。教学重点理解并掌握圆柱体积计算公式,并能应用公式计算圆柱的体积。
重点 对圆柱体体积公式的理解题。
难点 圆柱体体积的推倒过程。
学情分析 六年级学生已具备一定的自主探究的能力,思维形式也从形象思维为主慢慢向抽象思维为主发展,但是学生的空间思维能力还很有限。由于圆柱体积的计算需要通过转换来推导,所以在这个推导过程中,创设具体生动的问题情境,再利用课件直观演示,才能让学生真正感悟和掌握。
核心素养 应用已有知识解决实际问题的能力,发展空间观念和初步的推理能力。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 师:同学们,体育课后,小明口渴难耐,急匆匆的来到学校小卖部买饮料,老板拿出两种不同大小的杯装饮料让小明选择。(出示圆柱体形状的两个杯子),这两杯饮料同样多吗?哪个装的饮料更多一些呢?小明该怎么选呢? 利用生活中的例子引出今天的课题,围绕自主思考展开。 引入案例,使学生感兴趣,自然而然地导入本课的教学,起到引起学生注意,激发学生学习动机的效果;同时,也培养了学生在生活中学数学用数学的意识。
讲授新课 一、圆柱的体积 1、 1)教师:请同学们分别计算对比长方体和正方体的体积。 学生自主思考,并交流三分钟。 指名学生回答问题。 2、教师提问:圆柱体积的大小可能跟哪些条件有关? 学生自主思考,并交流三分钟。 指名学生回答问题。 教师过渡:同学们说的都有道理,我们来看看下面两组圆柱。 1)观察:①甲乙两个圆柱有什么相同?什么不同? 学生自主思考,并交流三分钟。 指名学生回答问题。 ②当高相等时,甲的体积为什么比乙的大? 学生自主思考,并交流三分钟。 指名学生回答问题。 教师讲解:S甲=S乙, h甲>h乙, V甲>V乙。圆柱的高相等,底面积大的体积就大。 2)观察:①甲乙两个圆柱有什么相同?什么不同? 学生自主思考,并交流三分钟。 指名学生回答问题。 ②当底面积相等时,甲的体积为什么比乙的要大? 学生自主思考,并交流三分钟。 指名学生回答问题。 教师讲解: 底面积:S甲=S乙, h甲>h乙, V甲>V乙。圆柱的底面积相等,高越长体积就越大。 教师总结:圆柱体积的大小与圆柱的底面积和高有关。 二、圆柱体积的推导 1、教师提问:要怎样求圆柱的体积呢? 学生自主思考,并交流三分钟。 指名学生回答问题。 过渡:有些同学预习的很不错,不懂的同学就要认真听讲。 教师提问:下面长方体、正方体和圆柱的底面积相等,高也相等。 教师讲解:长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长(高) V= s h 教师提问:长方体和正方体的体积相等吗?圆柱的体积与长方体、正方体的体积相等吗?用什么办法验证呢?组内讨论。 (1)用什么方法,把圆柱体转化成我们学过的立体图形? (2)在这个转化的过程中,什么变了,什么没有变? (3)这个长方体的底面积等于圆柱的什么 (4)长方体的高与圆柱体的高有什么关系? 学生自主思考,并交流三分钟。 指名学生回答问题。 教师讲解圆柱转化过程: ①把圆柱的底面平均分成16份。 ②把圆柱的底面平均分成32份。 ③把圆柱的底面平均分成64份。 教师总结:平均分的份数越多,拼成的物体就越接近长方体。 教师提问:圆可以转化成近似的长方形计算面积,圆柱可以转化成近似的长方体计算体积吗? 学生自主思考,邀请学生回答问题。 教师讲解: 教师提问:把圆柱体转化成长方体的过程中,体积不变,表面积增加了多少呢? 学生自主思考,邀请学生回答问题。 教师讲解: 三、合作探究 1、 教师提问:将一个圆柱切开后拼成一个近似的长方体后(如图),表面积增加了48平方厘米,已知长方体的高是6厘米,圆柱体的体积是多少立方厘米? 学生自主完成题目,并和同桌交流你为什么这么做。教师巡视。 指名学生回答问题。 教师讲解:利用今天所学的公式我们就可以得到我们想要的答案.V=Sh,我们要求S,首先就要知道底面半径,r=48÷6÷2=4(cm),然后代入V=Sh=4*4*3.14*6=301.44(cm3) 2、找错误 学生自主完成题目,并和同桌交流你为什么这么做。 指名学生回答问题。 教师总结:①求底面积时没有乘半径的平方。 ②单位错误,体积单位要加立方。 3、教师提问:回顾圆柱体积公式的探索过程,你有什么体会? 指名学生回答问题。 四、课堂练习 1. 把一个大圆柱分成两个小圆柱后发生变化的是( )。 A.圆柱的体积 B.圆柱的表面积 C.圆柱的底面积 2.一个长方形的长是6 cm,宽是4 cm,如图所示,以长为轴旋转一周形成圆柱甲,以宽为轴旋转一周形成圆柱乙,下面说法正确的是( )。 A.圆柱甲的底面积比圆柱乙的底面积大 B.圆柱甲的表面积和圆柱乙的表面积相等 C.圆柱甲的体积比圆柱乙的体积小 3.一个圆柱形输油管,内直径是2dm,油充满整个管内的流速是4分米/秒,每秒流过的油是( )cm 。 A.62.8 B.2.512 C.12560 4.判断题 (1)侧面积相等的圆柱,它们的体积也一定相等。( ) (2)一个圆柱和一个长方体的底面积和高分别相等,它们的体积一定相等。( ) (3)圆柱的体积一般比它的表面积大。( ) (4)底面积相等的两个圆柱,它们的体积也一定相等。 ( ) (5)圆柱的底面半径扩大到原来的2倍,高也扩大到原来的2倍,则圆柱的体积扩大到原来的4倍。 ( ) 5.夏日炎炎,小红自己装了满满一瓶橙汁饮料,主体直径是5cm(饮料瓶壁厚度忽略不计)。小红喝了一些后,水的高度还有12cm,把瓶盖拧紧后倒置平放,无水部分高10cm。
(1)小红喝了多少饮料? (2)这个橙汁瓶子上原来贴了一图宽为6厘米的商标纸,这个商标纸的面积是多少平方厘米?(接缝处粘贴部分的宽为1厘米) 学生自主完成题目。 学生通过观察,进行自主思考。指名学生回答问题。教师讲解,学生认真听讲。 学生自主思考,指明学生回答问题。 教师讲解,学生认真听讲。 学生自主思考,指名学生回答问题,教师讲解,学生认真听讲。 学生自主思考,教师巡视,指名学生回答问题。教师讲解。学生认真听讲。 由长方体和正方体和体积公式入手,通过复习,巩固这种两立体图形的体积,为推导圆柱的体积做好知识准备 通过教师提问,以及学生实际观察,自主思考,有利于培养学生的自主思考能力。 通过教师提问,学生自主思考,一步一步联想到圆柱,有利于本课知识的掌握,教师讲解,巩固知识。 运用多媒体技术,形象生动地展示“平均分成的分数越多,拼成的立体图形就越接近于长方体”,这里转化思想和极限思想得到应有的体现,同时也渗透了以直代曲的观点,又发展了学生的空间观念。 数学教学活动建立在学生的认知发展水平和已有的知识经验基础之上。由复习圆面积公式的推导过程入手,实现知识的迁移。 通过一系列问题,巩固知识——求体积,找错,不同条件对应求解方式不一样。且有利于提高学生思考做题能力以及团队和做能力。 回顾圆柱体积公式的探索过程,感受所学数学知识的应用价值。
课堂小结 这节课我们学会了什么? 1.圆柱体积公式的推导过程。 2.会用公式计算圆柱体积。 3.通过本课的数学知识,可以解决生活实际问题。
板书 解决实际问题 长方体的体积=底面积×高 圆柱的体积=底面积×高 V= S× h
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《圆柱和圆锥》单元整体教学设计
单元名称 苏教版六年级下册第二单元:《圆柱和圆锥》
课程标准分析 《圆柱与圆锥》单元是图形与几何领域第三学段“图形与几何”中的重要内容。《课程标准》在“内容要求”提出了: 1.通过实例了解圆柱、圆锥体积 (或容积)的意义,知道圆柱、圆锥体积(或容积)的度量单位,能进行单位之间的换算;体验不规则物体体积的测量方法 2.认识圆柱和圆锥,了解圆柱的展开图,探索并掌握圆柱的体积和表面积的计算公式,探索圆锥体积的计算公式,能用这些公式解决生活中的实际问题。 《课程标准》在“学业要求”中指出:认识圆柱和圆锥,能说出圆柱和圆锥的特征,能辨认这些圆柱的展开图,会计算圆柱的体积和表面积;会计算圆锥的体积;能用相应公式解决生活中实际问题。
内容分析 圆柱和圆锥都是平面与曲面围成的立体图形,是在圆的知识与长方体、正方体知识的基础上编排的,通过认识圆柱和圆锥的特征,理解圆柱侧面积和表面积的含义及计算方法,探索并应用圆柱和圆锥的体积计算公式,进一步发展空间观念和思维能力。
单元目标 一、单元目标拟定 1.认识圆柱和圆锥,掌握其特征和几个部分的名称与特点,建立几何模型。 2.认识圆柱的侧面及其展开图,并掌握侧面展开的长方形与圆柱相对应部分的关系。 3.熟练掌握圆柱表面积、圆柱体积、圆锥体积的计算公式,理解圆柱表面积、圆柱、体积、圆锥体积的知识在日常生活中的应用。感受数学知识与实际生活的密切联系,体会学习数学的乐趣。 二、关键内容确定 (一)教学重点 圆柱的表面积、体积的计算;圆锥体积的计算。 (二)教学难点 圆柱的表面积和体积的计算公式的推导;圆锥体积的计算公式的推导;圆柱与圆锥的体积之间的关系。
单元整体教学思路 组织本单元学习内容的思路如下:
苏教版数学六年级下第二单元第三课时教学设计
课题 圆柱的体积 单元 二 学 科 数 学 年 级 六
学习目标 1、运用迁移规律,引导学生借助圆面积计算公式的推导方法来推导圆柱的体积计算公式,会用圆柱的体积计算圆柱形物体的体积和容积。 2、经历猜测、验证、合作、动手操作等过程,体验和理解圆柱体体积公式的推导过程。 3、创设情境,激发学生学习的积极性。让学生在主动学习的基础上,逐步学会转化的数学思想和数学法,培养学生解决实际问题的能力和,培养学生抽象、概括的思维能力。教学重点理解并掌握圆柱体积计算公式,并能应用公式计算圆柱的体积。
重点 对圆柱体体积公式的理解题。
难点 圆柱体体积的推倒过程。
学情分析 六年级学生已具备一定的自主探究的能力,思维形式也从形象思维为主慢慢向抽象思维为主发展,但是学生的空间思维能力还很有限。由于圆柱体积的计算需要通过转换来推导,所以在这个推导过程中,创设具体生动的问题情境,再利用课件直观演示,才能让学生真正感悟和掌握。
核心素养 应用已有知识解决实际问题的能力,发展空间观念和初步的推理能力。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 师:同学们,体育课后,小明口渴难耐,急匆匆的来到学校小卖部买饮料,老板拿出两种不同大小的杯装饮料让小明选择。(出示圆柱体形状的两个杯子),这两杯饮料同样多吗?哪个装的饮料更多一些呢?小明该怎么选呢? 利用生活中的例子引出今天的课题,围绕自主思考展开。 引入案例,使学生感兴趣,自然而然地导入本课的教学,起到引起学生注意,激发学生学习动机的效果;同时,也培养了学生在生活中学数学用数学的意识。
讲授新课 一、圆柱的体积 1、 1)教师:请同学们分别计算对比长方体和正方体的体积。 学生自主思考,并交流三分钟。 指名学生回答问题。 2、教师提问:圆柱体积的大小可能跟哪些条件有关? 学生自主思考,并交流三分钟。 指名学生回答问题。 教师过渡:同学们说的都有道理,我们来看看下面两组圆柱。 1)观察:①甲乙两个圆柱有什么相同?什么不同? 学生自主思考,并交流三分钟。 指名学生回答问题。 ②当高相等时,甲的体积为什么比乙的大? 学生自主思考,并交流三分钟。 指名学生回答问题。 教师讲解:S甲=S乙, h甲>h乙, V甲>V乙。圆柱的高相等,底面积大的体积就大。 2)观察:①甲乙两个圆柱有什么相同?什么不同? 学生自主思考,并交流三分钟。 指名学生回答问题。 ②当底面积相等时,甲的体积为什么比乙的要大? 学生自主思考,并交流三分钟。 指名学生回答问题。 教师讲解: 底面积:S甲=S乙, h甲>h乙, V甲>V乙。圆柱的底面积相等,高越长体积就越大。 教师总结:圆柱体积的大小与圆柱的底面积和高有关。 二、圆柱体积的推导 1、教师提问:要怎样求圆柱的体积呢? 学生自主思考,并交流三分钟。 指名学生回答问题。 过渡:有些同学预习的很不错,不懂的同学就要认真听讲。 教师提问:下面长方体、正方体和圆柱的底面积相等,高也相等。 教师讲解:长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长(高) V= s h 教师提问:长方体和正方体的体积相等吗?圆柱的体积与长方体、正方体的体积相等吗?用什么办法验证呢?组内讨论。 (1)用什么方法,把圆柱体转化成我们学过的立体图形? (2)在这个转化的过程中,什么变了,什么没有变? (3)这个长方体的底面积等于圆柱的什么 (4)长方体的高与圆柱体的高有什么关系? 学生自主思考,并交流三分钟。 指名学生回答问题。 教师讲解圆柱转化过程: ①把圆柱的底面平均分成16份。 ②把圆柱的底面平均分成32份。 ③把圆柱的底面平均分成64份。 教师总结:平均分的份数越多,拼成的物体就越接近长方体。 教师提问:圆可以转化成近似的长方形计算面积,圆柱可以转化成近似的长方体计算体积吗? 学生自主思考,邀请学生回答问题。 教师讲解: 教师提问:把圆柱体转化成长方体的过程中,体积不变,表面积增加了多少呢? 学生自主思考,邀请学生回答问题。 教师讲解: 三、合作探究 1、 教师提问:将一个圆柱切开后拼成一个近似的长方体后(如图),表面积增加了48平方厘米,已知长方体的高是6厘米,圆柱体的体积是多少立方厘米? 学生自主完成题目,并和同桌交流你为什么这么做。教师巡视。 指名学生回答问题。 教师讲解:利用今天所学的公式我们就可以得到我们想要的答案.V=Sh,我们要求S,首先就要知道底面半径,r=48÷6÷2=4(cm),然后代入V=Sh=4*4*3.14*6=301.44(cm3) 2、找错误 学生自主完成题目,并和同桌交流你为什么这么做。 指名学生回答问题。 教师总结:①求底面积时没有乘半径的平方。 ②单位错误,体积单位要加立方。 3、教师提问:回顾圆柱体积公式的探索过程,你有什么体会? 指名学生回答问题。 四、课堂练习 1. 把一个大圆柱分成两个小圆柱后发生变化的是( )。 A.圆柱的体积 B.圆柱的表面积 C.圆柱的底面积 2.一个长方形的长是6 cm,宽是4 cm,如图所示,以长为轴旋转一周形成圆柱甲,以宽为轴旋转一周形成圆柱乙,下面说法正确的是( )。 A.圆柱甲的底面积比圆柱乙的底面积大 B.圆柱甲的表面积和圆柱乙的表面积相等 C.圆柱甲的体积比圆柱乙的体积小 3.一个圆柱形输油管,内直径是2dm,油充满整个管内的流速是4分米/秒,每秒流过的油是( )cm 。 A.62.8 B.2.512 C.12560 4.判断题 (1)侧面积相等的圆柱,它们的体积也一定相等。( ) (2)一个圆柱和一个长方体的底面积和高分别相等,它们的体积一定相等。( ) (3)圆柱的体积一般比它的表面积大。( ) (4)底面积相等的两个圆柱,它们的体积也一定相等。 ( ) (5)圆柱的底面半径扩大到原来的2倍,高也扩大到原来的2倍,则圆柱的体积扩大到原来的4倍。 ( ) 5.夏日炎炎,小红自己装了满满一瓶橙汁饮料,主体直径是5cm(饮料瓶壁厚度忽略不计)。小红喝了一些后,水的高度还有12cm,把瓶盖拧紧后倒置平放,无水部分高10cm。
(1)小红喝了多少饮料? (2)这个橙汁瓶子上原来贴了一图宽为6厘米的商标纸,这个商标纸的面积是多少平方厘米?(接缝处粘贴部分的宽为1厘米) 学生自主完成题目。 学生通过观察,进行自主思考。指名学生回答问题。教师讲解,学生认真听讲。 学生自主思考,指明学生回答问题。 教师讲解,学生认真听讲。 学生自主思考,指名学生回答问题,教师讲解,学生认真听讲。 学生自主思考,教师巡视,指名学生回答问题。教师讲解。学生认真听讲。 由长方体和正方体和体积公式入手,通过复习,巩固这种两立体图形的体积,为推导圆柱的体积做好知识准备 通过教师提问,以及学生实际观察,自主思考,有利于培养学生的自主思考能力。 通过教师提问,学生自主思考,一步一步联想到圆柱,有利于本课知识的掌握,教师讲解,巩固知识。 运用多媒体技术,形象生动地展示“平均分成的分数越多,拼成的立体图形就越接近于长方体”,这里转化思想和极限思想得到应有的体现,同时也渗透了以直代曲的观点,又发展了学生的空间观念。 数学教学活动建立在学生的认知发展水平和已有的知识经验基础之上。由复习圆面积公式的推导过程入手,实现知识的迁移。 通过一系列问题,巩固知识——求体积,找错,不同条件对应求解方式不一样。且有利于提高学生思考做题能力以及团队和做能力。 回顾圆柱体积公式的探索过程,感受所学数学知识的应用价值。
课堂小结 这节课我们学会了什么? 1.圆柱体积公式的推导过程。 2.会用公式计算圆柱体积。 3.通过本课的数学知识,可以解决生活实际问题。
板书 解决实际问题 长方体的体积=底面积×高 圆柱的体积=底面积×高 V= S× h
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
