人教版七年级下册 第5章 相交线与平行线 单元检测卷 含解析
文档属性
| 名称 | 人教版七年级下册 第5章 相交线与平行线 单元检测卷 含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 379.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 21:33:48 | ||
图片预览


文档简介
人教版七年级下册 第5章 相交线与平行线 单元检测卷
满分100分
一.选择题(共10小题,满分30分,每小题3分)
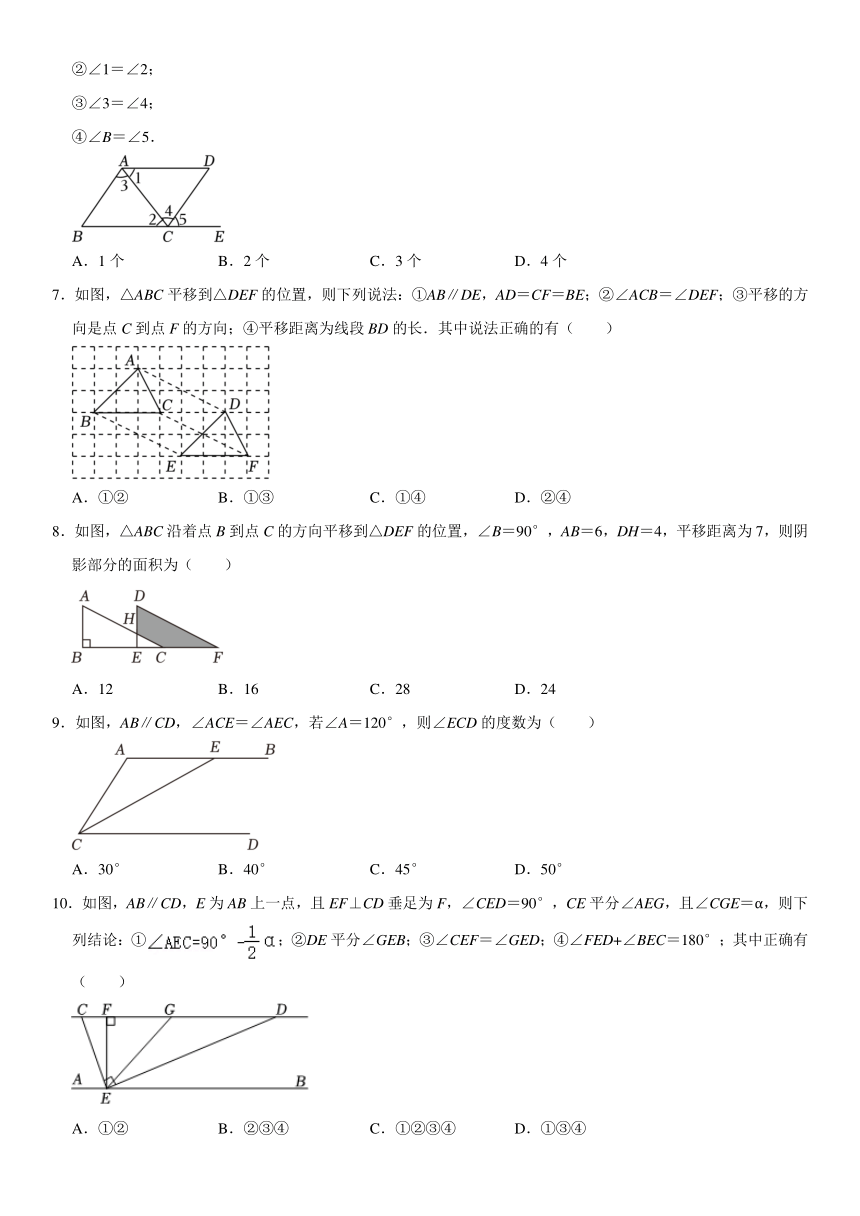
1.下列运动属于平移的是( )
A.荡秋千 B.转动中的电风扇叶片
C.地球绕着太阳转 D.急刹车时,汽车在地面上的滑动
2.下列图形中,∠1与∠2不是同位角的是( )
A. B.
C. D.
3.如图,直线AB,CD相交于点O,EO⊥CD于点O,若∠1=55°,则∠2的度数为( )
A.25° B.35° C.45° D.55°
4.下列各图中,能画出AB∥CD的是( )
A.①②③ B.①②④ C.③④ D.①②③④
5.下列命题属于真命题的是( )
A.同一平面内,两条直线的位置关系是垂直和相交
B.过一点有且只有一条直线与已知直线垂直
C.两直线平行,同旁内角的角平分线互相平行
D.平移前后对应点所连线段的关系是平行(或共线)且相等
6.如图,下列能判定AB∥CD的条件有( )
①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
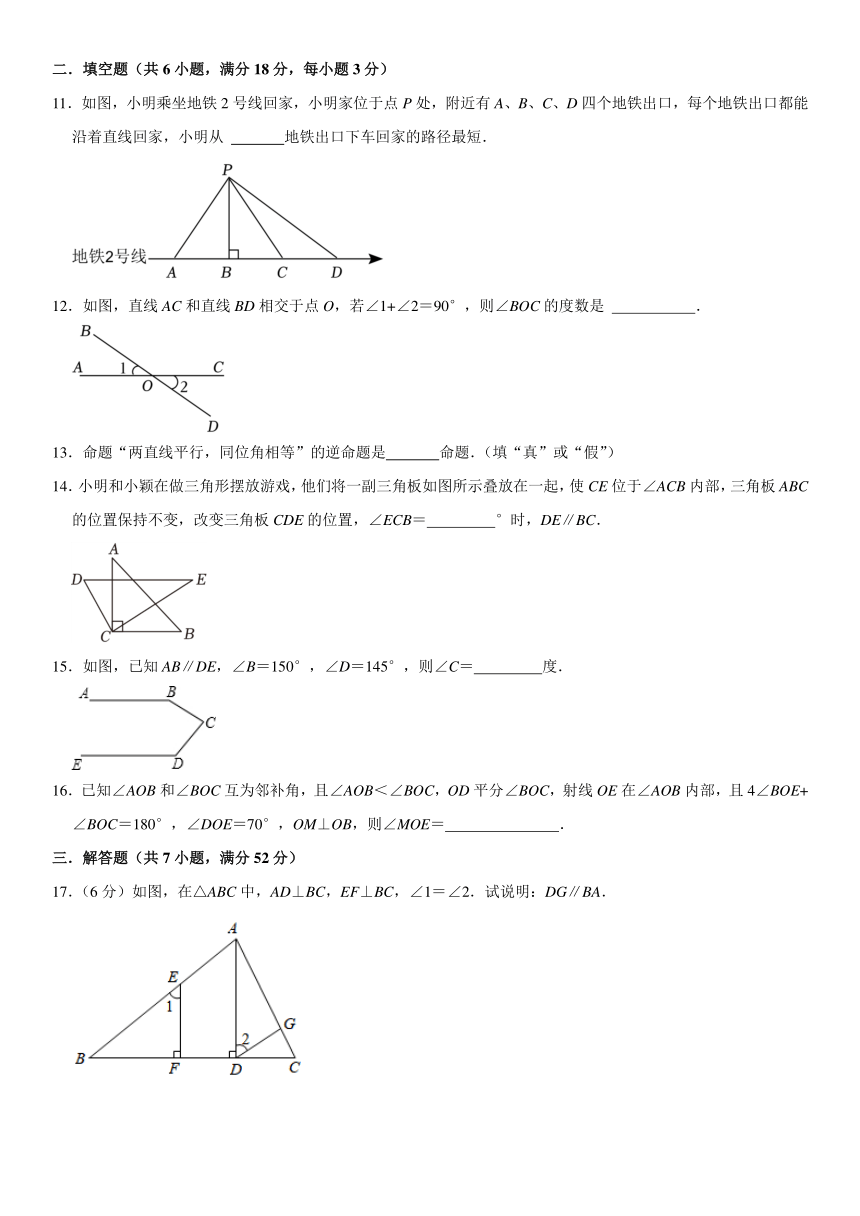
7.如图,△ABC平移到△DEF的位置,则下列说法:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点F的方向;④平移距离为线段BD的长.其中说法正确的有( )
A.①② B.①③ C.①④ D.②④
8.如图,△ABC沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=6,DH=4,平移距离为7,则阴影部分的面积为( )
A.12 B.16 C.28 D.24
9.如图,AB∥CD,∠ACE=∠AEC,若∠A=120°,则∠ECD的度数为( )
A.30° B.40° C.45° D.50°
10.如图,AB∥CD,E为AB上一点,且EF⊥CD垂足为F,∠CED=90°,CE平分∠AEG,且∠CGE=α,则下列结论:①;②DE平分∠GEB;③∠CEF=∠GED;④∠FED+∠BEC=180°;其中正确有( )
A.①② B.②③④ C.①②③④ D.①③④
二.填空题(共6小题,满分18分,每小题3分)
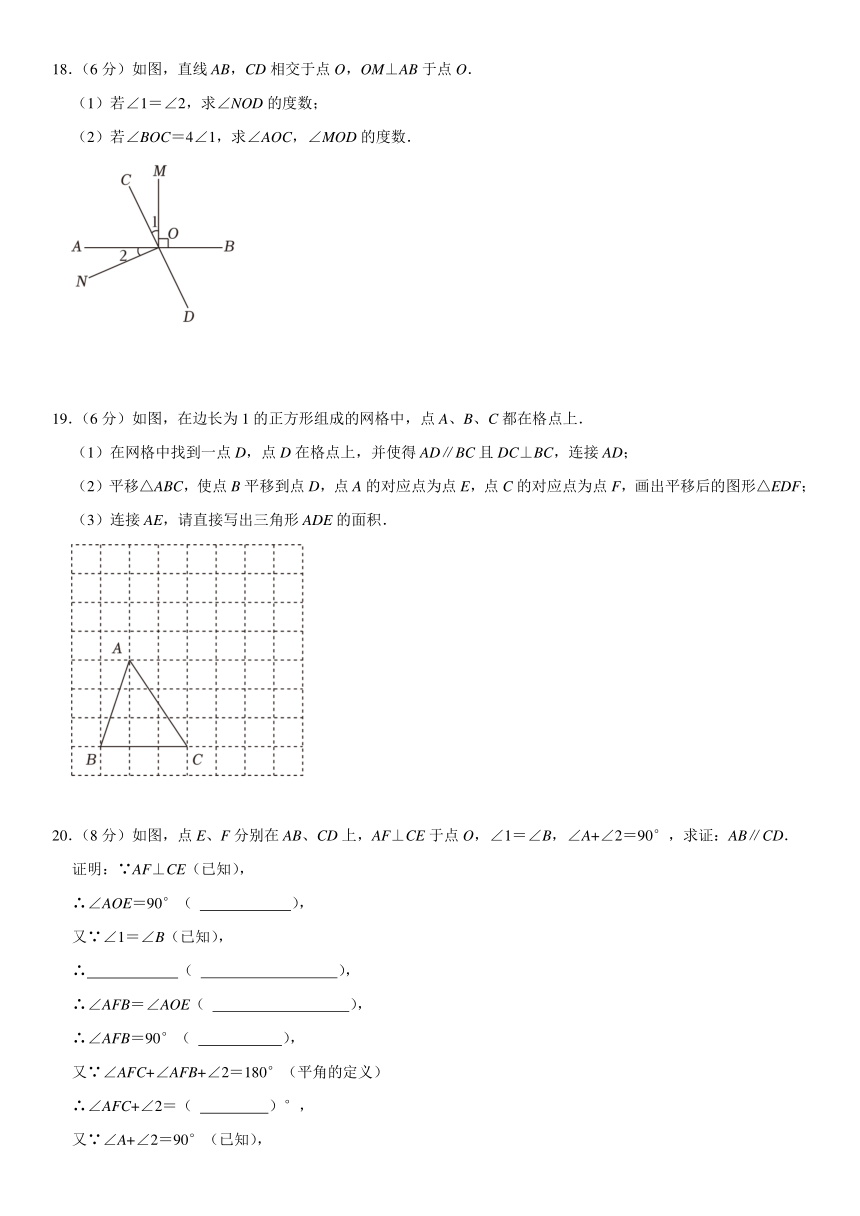
11.如图,小明乘坐地铁2号线回家,小明家位于点P处,附近有A、B、C、D四个地铁出口,每个地铁出口都能沿着直线回家,小明从 地铁出口下车回家的路径最短.
12.如图,直线AC和直线BD相交于点O,若∠1+∠2=90°,则∠BOC的度数是 .
13.命题“两直线平行,同位角相等”的逆命题是 命题.(填“真”或“假”)
14.小明和小颖在做三角形摆放游戏,他们将一副三角板如图所示叠放在一起,使CE位于∠ACB内部,三角板ABC的位置保持不变,改变三角板CDE的位置,∠ECB= °时,DE∥BC.
15.如图,已知AB∥DE,∠B=150°,∠D=145°,则∠C= 度.
16.已知∠AOB和∠BOC互为邻补角,且∠AOB<∠BOC,OD平分∠BOC,射线OE在∠AOB内部,且4∠BOE+∠BOC=180°,∠DOE=70°,OM⊥OB,则∠MOE= .
三.解答题(共7小题,满分52分)
17.(6分)如图,在△ABC中,AD⊥BC,EF⊥BC,∠1=∠2.试说明:DG∥BA.
18.(6分)如图,直线AB,CD相交于点O,OM⊥AB于点O.
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠BOC=4∠1,求∠AOC,∠MOD的度数.
19.(6分)如图,在边长为1的正方形组成的网格中,点A、B、C都在格点上.
(1)在网格中找到一点D,点D在格点上,并使得AD∥BC且DC⊥BC,连接AD;
(2)平移△ABC,使点B平移到点D,点A的对应点为点E,点C的对应点为点F,画出平移后的图形△EDF;
(3)连接AE,请直接写出三角形ADE的面积.
20.(8分)如图,点E、F分别在AB、CD上,AF⊥CE于点O,∠1=∠B,∠A+∠2=90°,求证:AB∥CD.
证明:∵AF⊥CE(已知),
∴∠AOE=90°( ),
又∵∠1=∠B(已知),
∴ ( ),
∴∠AFB=∠AOE( ),
∴∠AFB=90°( ),
又∵∠AFC+∠AFB+∠2=180°(平角的定义)
∴∠AFC+∠2=( )°,
又∵∠A+∠2=90°(已知),
∴∠A=∠AFC( ),
∴AB∥CD.( )
21.(8分)如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,
(1)求证:EF∥CD;
(2)求证:∠1=∠2.
22.(9分)如图,MN∥OP,点A为直线MN上一定点,B为直线OP上的动点,在直线MN与OP之间且在线段AB的右方作点D,使得AD⊥BD.设∠DAB=α(α为锐角).
(1)求∠NAD与∠PBD的和;(提示过点D作EF∥MN)
(2)当点B在直线OP上运动时,试说明∠OBD﹣∠NAD=90°;
(3)当点B在直线OP上运动的过程中,若AD平分∠NAB,AB也恰好平分∠OBD,请求出此时α的值
23.(9分)某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:
已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,运用上述结论,探究∠PEQ与∠APE+∠CQE之间的数量关系.并说明理由;
(2)如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=130°时,求出∠PFQ的度数;
(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F,当∠PEQ=80°时,请直接写出∠PFQ的度数.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、荡秋千,属于旋转变换,不符合题意;
B、转动中的电风扇叶片,属于旋转变换,不符合题意;
C、地球绕着太阳转,属于旋转变换,不符合题意;
D、急刹车时,汽车在地面上的滑动,属于平移变换,符合题意;
故选:D.
2.解:A、∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
B、∠1与∠2的两条边都不在同一条直线上,不是同位角,符合题意;
C、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
D、∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意.
故选:B.
3.解:∵EO⊥CD,
∴∠EOD=90°,
∵∠1=55°,
∴∠BOD=∠EOD﹣∠1=90°﹣55°=35°,
∴∠2=∠BOD=35°,
故选:B.
4.解:由同位角相等两直线平行可知:①正确;由垂直于同一条直线的两条直线平行可知②、③正确;根据内错角相等两直线平行线可知④正确.
故选:D.
5.解:同一平面内,两条直线的位置关系是平行和相交,故A是假命题,不符合题意;
在平面内,过一点有且只有一条直线与已知直线垂直,故B是假命题,不符合题意;
两直线平行,同旁内角的角平分线互相垂直,故C是假命题,不符合题意;
平移前后对应点所连线段的关系是平行(或共线)且相等,故D是真命题,符合题意;
故选:D.
6.解:①∵∠B+∠BCD=180°,
∴AB∥CD,
故①符合题意;
②∵∠1=∠2,
∴AD∥BC,
故②不符合题意;
③∵∠3=∠4,
∴AB∥CD,
故③符合题意;
④∵∠B=∠5,
∴AB∥CD,
故④符合题意;
综上,①③④符合题意,共3个,
故选:C.
7.解:由平移的性质可知,
①AB∥DE,AD=CF=BE,因此正确;
②由平移的性质可知,∠ACB=∠DFE,因此②不正确;
③平移的方向是点C到点F的方向或点A到点D的方向或点B到点E的方向,因此正确;
④平移距离为线段BE或线段AD或线段CF的长,因此④不正确;
综上所述,正确的结论有:①③,
故选:B.
8.解:∵平移距离为7,
∴BE=7,
∵AB=6,DH=4,
∴EH=6﹣4=2,
∵S△ABC=S△DEF,
∴S四边形ABEH=S阴,
∴阴影部分的面积为=×(6+2)×7=28.
故选:C.
9.解∵∠A=120°,
∴∠AEC=×(180°﹣∠A)=30°,
∵AB∥CD,
∴∠ECD=∠AEC=30°.
故选:A.
10.解:∵∠CGE=a,AB∥CD,
∴∠CGE=∠GEB=a,
∴∠AEG=180°﹣a,
∵CE平分∠AEG,
∴∠AEC=∠CEG=∠AEG=90°﹣a,
故①正确;
∵∠CED=90°,
∴∠AEC+∠DEB=90°,
∴∠DEB=a=∠GEB,
即DE平分∠GEB,
故②正确;
∵EF⊥CD,AB∥CD,
∴∠AEF=90°,
∴∠AEC+∠CEF=90°,
∴∠CEF=a,
∵∠GED=∠GEB﹣∠DEB=a,
∴∠CEF=∠GED,
故③正确;
∵∠FED=90°﹣∠BED=90°﹣a,
∠BEC=180°﹣∠AEC=90°+a,
∴∠FED+∠BEC=180°,
故④正确;
综上所述,正确的有①②③④,
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.解:根据“垂线段最短”的性质,可得PB最短.
故答案为:B.
12.解:∵∠1=∠2,∠1+∠2=90°,
∴∠1=∠2=45°,
∴∠BOC=180°﹣45°=135°.
13.解:∵原命题的条件为:两直线平行,结论为:同位角相等.
∴其逆命题为:同位角相等,两直线平行,正确,为真命题,
故答案为:真.
14.解:∵∠E=30°,
∴∠ECB=30°时,DE∥BC.
故答案为:30.
15.解:过点C作CF平行于AB,如图:
∵AB∥DE,
∴AB∥CF∥ED.
AB∥CF ∠1=180°﹣∠B=30°,
CF∥ED ∠2=180°﹣∠D=35°,
∴∠BCD=∠1+∠2=65°.
故填65°.
16.解:分两种情况进行讨论:
①如图1所示,若OM在AC上方,
∵OD平分∠BOC,
∴∠COD=∠BOD,
∵4∠BOE+∠BOC=180°,∠AOB+∠BOC=180°,
∴∠AOB=4∠BOE,即∠AOE=3∠BOE,
设∠BOE=α,则∠AOE=3α,∠BOD=70°﹣α=∠COD,
∵∠AOC为平角,
∴∠AOE+∠DOE+∠COD=180°,
即3α+70°+70°﹣α=180°,
解得α=20°,
∴∠BOE=20°,
又∵OM⊥OB,
∴∠MOB=90°,
∴∠MOE=∠BOE+∠MOB=20°+90°=110°;
②如图2所示,若OM在AC下方,
同理可得,∠BOE=20°,
又∵OM⊥OB,
∴∠MOB=90°,
∴∠MOE=∠MOB﹣∠BOE=90°﹣20°=70°;
综上所述,∠MOE的度数为110°或70°.
故答案为:110°或70°.
三.解答题(共7小题,满分52分)
17.证明:∵AD⊥BC,EF⊥BC,
∴∠EFB=∠ADB=90°,
∴EF∥AD,
∴∠1=∠BAD,
又∵∠1=∠2,
∴∠2=∠BAD,
∴DG∥AB.
18.解:(1)∵OM⊥AB,
∴∠AOM=90°,
∴∠AOC+∠1=90°,
∵∠1=∠2,
∴∠AOC+∠2=90°,即∠NOC=90°,
∴∠NOD=180°﹣∠NOC=90°.
∴∠NOD的度数为90°;
(2)∵OM⊥AB,
∴∠BOM=90°,
∵∠BOC=4∠1,
∴∠BOM+∠1=4∠1,即90°+∠1=4∠1,
解得∠1=30°,
∴∠AOC=90°﹣30°=60°,∠MOD=180°﹣∠1=150°.
∴∠AOC的度数为60°,∠MOD的度数为150°.
19.解:(1)如图,点D即为所求.
(2)如图,△EDF即为所求.
(3)三角形ADE的面积为=3.
20.证明:∵AF⊥CE(已知),
∴∠AOE=90°(垂直的定义),
∵∠1=∠B(已知),
∴CE∥BF(同位角相等,两直线平行),
∴∠AFB=∠AOE(两直线平行,同位角相等),
∴∠AFB=90°(等量代换),
∵∠AFC+∠AFB+∠2=180°(平角的定义),
∴∠AFC+∠2=(90)°,
∵∠A+∠2=90°(已知),
∴∠A=∠AFC(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
故答案为:垂直的定义;CE∥BF;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;90;同角的余角相等;内错角相等,两直线平行.
21.证明:
(1)∵EF⊥AB于F,CD⊥AB于D,
∴∠BFE=∠BDC=90°,
∴EF∥CD;
(2)∵EF∥CD,
∴∠2=∠3,
∵∠AGD=∠ACB,
∴DG∥BC,
∴∠1=∠3
∴∠1=∠2.
22.解:(1)如图,过点D作EF∥MN,则∠NAD=∠ADE.
∵MN∥OP,EF∥MN,
∴EF∥OP.
∴∠PBD=∠BDE,
∴∠NAD+∠PBD=∠ADE+∠BDE=∠ADB.
∵AD⊥BD,
∴∠ADB=90°,
∴∠NAD+∠PBD=90°.
(2)由(1)得:∠NAD+∠PBD=90°,则∠NAD=90°﹣∠PBD.
∵∠OBD+∠PBD=180°,
∴∠OBD=180°﹣∠PBD,
∴∠OBD﹣∠NAD=(180°﹣∠PBD)﹣(90°﹣∠PBD)=90°.
(3)若AD平分∠NAB,AB也恰好平分∠OBD,则有∠NAD=∠BAD=α,∠NAB=2∠BAD=2α,∠OBD=2∠OBA.
∵OP∥MN,
∴∠OBA=∠NAB=2α,
∴∠OBD=4α.
由(2)知:∠OBD﹣∠NAD=90°,则4α﹣α=90°,解得:α=30°.
23.解:(1)∠PEQ=∠APE+∠CQE,
如图1,过点E作EH∥AB,则EH∥AB∥CD,
∵AB∥EH,
∴∠APE=∠PEH,
又∵CD∥EH,
∴∠CQE=∠HEQ,
∵∠PEQ=∠PEH+HEQ,
∴∠PEQ=∠APE+∠CQE;
(2)如图2,由(1)得,∠PEQ=∠APE+∠CQE=130°;
∵∠APE+∠BPE=180°,∠CQE+∠DQE=180°,
∴∠BPE+∠DQE=360°﹣130°=230°,
又∵PF平分∠BPE,QF平分∠EQD,
∴∠1=∠2,∠3=∠4,
∴∠1+∠3=(∠BPE+∠DQE)=×230°=115°,
在四边形PEQF中,
∠PFQ=360°﹣(∠1+∠2+∠PEQ)=360°﹣(115°+130°)=115°;
(3)140°,如图3,延长PF交CD与点M,
∵PF平分∠BPE,QH平分∠EQD,
∴∠1=∠2,∠3=∠4,
∵AB∥CD,
∴∠BPE=∠DNE,∠2=∠PMC=∠1,
又∵∠DQE=∠DNE+∠E,即2∠4=2∠1+80°,
∴∠4﹣∠1=40°,
∴∠PFQ=∠FQD+∠PMC=180°﹣∠4+∠1=180°﹣(∠4﹣∠1)=180°﹣40°=140°.
满分100分
一.选择题(共10小题,满分30分,每小题3分)
1.下列运动属于平移的是( )
A.荡秋千 B.转动中的电风扇叶片
C.地球绕着太阳转 D.急刹车时,汽车在地面上的滑动
2.下列图形中,∠1与∠2不是同位角的是( )
A. B.
C. D.
3.如图,直线AB,CD相交于点O,EO⊥CD于点O,若∠1=55°,则∠2的度数为( )
A.25° B.35° C.45° D.55°
4.下列各图中,能画出AB∥CD的是( )
A.①②③ B.①②④ C.③④ D.①②③④
5.下列命题属于真命题的是( )
A.同一平面内,两条直线的位置关系是垂直和相交
B.过一点有且只有一条直线与已知直线垂直
C.两直线平行,同旁内角的角平分线互相平行
D.平移前后对应点所连线段的关系是平行(或共线)且相等
6.如图,下列能判定AB∥CD的条件有( )
①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
7.如图,△ABC平移到△DEF的位置,则下列说法:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点F的方向;④平移距离为线段BD的长.其中说法正确的有( )
A.①② B.①③ C.①④ D.②④
8.如图,△ABC沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=6,DH=4,平移距离为7,则阴影部分的面积为( )
A.12 B.16 C.28 D.24
9.如图,AB∥CD,∠ACE=∠AEC,若∠A=120°,则∠ECD的度数为( )
A.30° B.40° C.45° D.50°
10.如图,AB∥CD,E为AB上一点,且EF⊥CD垂足为F,∠CED=90°,CE平分∠AEG,且∠CGE=α,则下列结论:①;②DE平分∠GEB;③∠CEF=∠GED;④∠FED+∠BEC=180°;其中正确有( )
A.①② B.②③④ C.①②③④ D.①③④
二.填空题(共6小题,满分18分,每小题3分)
11.如图,小明乘坐地铁2号线回家,小明家位于点P处,附近有A、B、C、D四个地铁出口,每个地铁出口都能沿着直线回家,小明从 地铁出口下车回家的路径最短.
12.如图,直线AC和直线BD相交于点O,若∠1+∠2=90°,则∠BOC的度数是 .
13.命题“两直线平行,同位角相等”的逆命题是 命题.(填“真”或“假”)
14.小明和小颖在做三角形摆放游戏,他们将一副三角板如图所示叠放在一起,使CE位于∠ACB内部,三角板ABC的位置保持不变,改变三角板CDE的位置,∠ECB= °时,DE∥BC.
15.如图,已知AB∥DE,∠B=150°,∠D=145°,则∠C= 度.
16.已知∠AOB和∠BOC互为邻补角,且∠AOB<∠BOC,OD平分∠BOC,射线OE在∠AOB内部,且4∠BOE+∠BOC=180°,∠DOE=70°,OM⊥OB,则∠MOE= .
三.解答题(共7小题,满分52分)
17.(6分)如图,在△ABC中,AD⊥BC,EF⊥BC,∠1=∠2.试说明:DG∥BA.
18.(6分)如图,直线AB,CD相交于点O,OM⊥AB于点O.
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠BOC=4∠1,求∠AOC,∠MOD的度数.
19.(6分)如图,在边长为1的正方形组成的网格中,点A、B、C都在格点上.
(1)在网格中找到一点D,点D在格点上,并使得AD∥BC且DC⊥BC,连接AD;
(2)平移△ABC,使点B平移到点D,点A的对应点为点E,点C的对应点为点F,画出平移后的图形△EDF;
(3)连接AE,请直接写出三角形ADE的面积.
20.(8分)如图,点E、F分别在AB、CD上,AF⊥CE于点O,∠1=∠B,∠A+∠2=90°,求证:AB∥CD.
证明:∵AF⊥CE(已知),
∴∠AOE=90°( ),
又∵∠1=∠B(已知),
∴ ( ),
∴∠AFB=∠AOE( ),
∴∠AFB=90°( ),
又∵∠AFC+∠AFB+∠2=180°(平角的定义)
∴∠AFC+∠2=( )°,
又∵∠A+∠2=90°(已知),
∴∠A=∠AFC( ),
∴AB∥CD.( )
21.(8分)如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,
(1)求证:EF∥CD;
(2)求证:∠1=∠2.
22.(9分)如图,MN∥OP,点A为直线MN上一定点,B为直线OP上的动点,在直线MN与OP之间且在线段AB的右方作点D,使得AD⊥BD.设∠DAB=α(α为锐角).
(1)求∠NAD与∠PBD的和;(提示过点D作EF∥MN)
(2)当点B在直线OP上运动时,试说明∠OBD﹣∠NAD=90°;
(3)当点B在直线OP上运动的过程中,若AD平分∠NAB,AB也恰好平分∠OBD,请求出此时α的值
23.(9分)某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:
已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,运用上述结论,探究∠PEQ与∠APE+∠CQE之间的数量关系.并说明理由;
(2)如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=130°时,求出∠PFQ的度数;
(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F,当∠PEQ=80°时,请直接写出∠PFQ的度数.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、荡秋千,属于旋转变换,不符合题意;
B、转动中的电风扇叶片,属于旋转变换,不符合题意;
C、地球绕着太阳转,属于旋转变换,不符合题意;
D、急刹车时,汽车在地面上的滑动,属于平移变换,符合题意;
故选:D.
2.解:A、∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
B、∠1与∠2的两条边都不在同一条直线上,不是同位角,符合题意;
C、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
D、∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意.
故选:B.
3.解:∵EO⊥CD,
∴∠EOD=90°,
∵∠1=55°,
∴∠BOD=∠EOD﹣∠1=90°﹣55°=35°,
∴∠2=∠BOD=35°,
故选:B.
4.解:由同位角相等两直线平行可知:①正确;由垂直于同一条直线的两条直线平行可知②、③正确;根据内错角相等两直线平行线可知④正确.
故选:D.
5.解:同一平面内,两条直线的位置关系是平行和相交,故A是假命题,不符合题意;
在平面内,过一点有且只有一条直线与已知直线垂直,故B是假命题,不符合题意;
两直线平行,同旁内角的角平分线互相垂直,故C是假命题,不符合题意;
平移前后对应点所连线段的关系是平行(或共线)且相等,故D是真命题,符合题意;
故选:D.
6.解:①∵∠B+∠BCD=180°,
∴AB∥CD,
故①符合题意;
②∵∠1=∠2,
∴AD∥BC,
故②不符合题意;
③∵∠3=∠4,
∴AB∥CD,
故③符合题意;
④∵∠B=∠5,
∴AB∥CD,
故④符合题意;
综上,①③④符合题意,共3个,
故选:C.
7.解:由平移的性质可知,
①AB∥DE,AD=CF=BE,因此正确;
②由平移的性质可知,∠ACB=∠DFE,因此②不正确;
③平移的方向是点C到点F的方向或点A到点D的方向或点B到点E的方向,因此正确;
④平移距离为线段BE或线段AD或线段CF的长,因此④不正确;
综上所述,正确的结论有:①③,
故选:B.
8.解:∵平移距离为7,
∴BE=7,
∵AB=6,DH=4,
∴EH=6﹣4=2,
∵S△ABC=S△DEF,
∴S四边形ABEH=S阴,
∴阴影部分的面积为=×(6+2)×7=28.
故选:C.
9.解∵∠A=120°,
∴∠AEC=×(180°﹣∠A)=30°,
∵AB∥CD,
∴∠ECD=∠AEC=30°.
故选:A.
10.解:∵∠CGE=a,AB∥CD,
∴∠CGE=∠GEB=a,
∴∠AEG=180°﹣a,
∵CE平分∠AEG,
∴∠AEC=∠CEG=∠AEG=90°﹣a,
故①正确;
∵∠CED=90°,
∴∠AEC+∠DEB=90°,
∴∠DEB=a=∠GEB,
即DE平分∠GEB,
故②正确;
∵EF⊥CD,AB∥CD,
∴∠AEF=90°,
∴∠AEC+∠CEF=90°,
∴∠CEF=a,
∵∠GED=∠GEB﹣∠DEB=a,
∴∠CEF=∠GED,
故③正确;
∵∠FED=90°﹣∠BED=90°﹣a,
∠BEC=180°﹣∠AEC=90°+a,
∴∠FED+∠BEC=180°,
故④正确;
综上所述,正确的有①②③④,
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.解:根据“垂线段最短”的性质,可得PB最短.
故答案为:B.
12.解:∵∠1=∠2,∠1+∠2=90°,
∴∠1=∠2=45°,
∴∠BOC=180°﹣45°=135°.
13.解:∵原命题的条件为:两直线平行,结论为:同位角相等.
∴其逆命题为:同位角相等,两直线平行,正确,为真命题,
故答案为:真.
14.解:∵∠E=30°,
∴∠ECB=30°时,DE∥BC.
故答案为:30.
15.解:过点C作CF平行于AB,如图:
∵AB∥DE,
∴AB∥CF∥ED.
AB∥CF ∠1=180°﹣∠B=30°,
CF∥ED ∠2=180°﹣∠D=35°,
∴∠BCD=∠1+∠2=65°.
故填65°.
16.解:分两种情况进行讨论:
①如图1所示,若OM在AC上方,
∵OD平分∠BOC,
∴∠COD=∠BOD,
∵4∠BOE+∠BOC=180°,∠AOB+∠BOC=180°,
∴∠AOB=4∠BOE,即∠AOE=3∠BOE,
设∠BOE=α,则∠AOE=3α,∠BOD=70°﹣α=∠COD,
∵∠AOC为平角,
∴∠AOE+∠DOE+∠COD=180°,
即3α+70°+70°﹣α=180°,
解得α=20°,
∴∠BOE=20°,
又∵OM⊥OB,
∴∠MOB=90°,
∴∠MOE=∠BOE+∠MOB=20°+90°=110°;
②如图2所示,若OM在AC下方,
同理可得,∠BOE=20°,
又∵OM⊥OB,
∴∠MOB=90°,
∴∠MOE=∠MOB﹣∠BOE=90°﹣20°=70°;
综上所述,∠MOE的度数为110°或70°.
故答案为:110°或70°.
三.解答题(共7小题,满分52分)
17.证明:∵AD⊥BC,EF⊥BC,
∴∠EFB=∠ADB=90°,
∴EF∥AD,
∴∠1=∠BAD,
又∵∠1=∠2,
∴∠2=∠BAD,
∴DG∥AB.
18.解:(1)∵OM⊥AB,
∴∠AOM=90°,
∴∠AOC+∠1=90°,
∵∠1=∠2,
∴∠AOC+∠2=90°,即∠NOC=90°,
∴∠NOD=180°﹣∠NOC=90°.
∴∠NOD的度数为90°;
(2)∵OM⊥AB,
∴∠BOM=90°,
∵∠BOC=4∠1,
∴∠BOM+∠1=4∠1,即90°+∠1=4∠1,
解得∠1=30°,
∴∠AOC=90°﹣30°=60°,∠MOD=180°﹣∠1=150°.
∴∠AOC的度数为60°,∠MOD的度数为150°.
19.解:(1)如图,点D即为所求.
(2)如图,△EDF即为所求.
(3)三角形ADE的面积为=3.
20.证明:∵AF⊥CE(已知),
∴∠AOE=90°(垂直的定义),
∵∠1=∠B(已知),
∴CE∥BF(同位角相等,两直线平行),
∴∠AFB=∠AOE(两直线平行,同位角相等),
∴∠AFB=90°(等量代换),
∵∠AFC+∠AFB+∠2=180°(平角的定义),
∴∠AFC+∠2=(90)°,
∵∠A+∠2=90°(已知),
∴∠A=∠AFC(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
故答案为:垂直的定义;CE∥BF;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;90;同角的余角相等;内错角相等,两直线平行.
21.证明:
(1)∵EF⊥AB于F,CD⊥AB于D,
∴∠BFE=∠BDC=90°,
∴EF∥CD;
(2)∵EF∥CD,
∴∠2=∠3,
∵∠AGD=∠ACB,
∴DG∥BC,
∴∠1=∠3
∴∠1=∠2.
22.解:(1)如图,过点D作EF∥MN,则∠NAD=∠ADE.
∵MN∥OP,EF∥MN,
∴EF∥OP.
∴∠PBD=∠BDE,
∴∠NAD+∠PBD=∠ADE+∠BDE=∠ADB.
∵AD⊥BD,
∴∠ADB=90°,
∴∠NAD+∠PBD=90°.
(2)由(1)得:∠NAD+∠PBD=90°,则∠NAD=90°﹣∠PBD.
∵∠OBD+∠PBD=180°,
∴∠OBD=180°﹣∠PBD,
∴∠OBD﹣∠NAD=(180°﹣∠PBD)﹣(90°﹣∠PBD)=90°.
(3)若AD平分∠NAB,AB也恰好平分∠OBD,则有∠NAD=∠BAD=α,∠NAB=2∠BAD=2α,∠OBD=2∠OBA.
∵OP∥MN,
∴∠OBA=∠NAB=2α,
∴∠OBD=4α.
由(2)知:∠OBD﹣∠NAD=90°,则4α﹣α=90°,解得:α=30°.
23.解:(1)∠PEQ=∠APE+∠CQE,
如图1,过点E作EH∥AB,则EH∥AB∥CD,
∵AB∥EH,
∴∠APE=∠PEH,
又∵CD∥EH,
∴∠CQE=∠HEQ,
∵∠PEQ=∠PEH+HEQ,
∴∠PEQ=∠APE+∠CQE;
(2)如图2,由(1)得,∠PEQ=∠APE+∠CQE=130°;
∵∠APE+∠BPE=180°,∠CQE+∠DQE=180°,
∴∠BPE+∠DQE=360°﹣130°=230°,
又∵PF平分∠BPE,QF平分∠EQD,
∴∠1=∠2,∠3=∠4,
∴∠1+∠3=(∠BPE+∠DQE)=×230°=115°,
在四边形PEQF中,
∠PFQ=360°﹣(∠1+∠2+∠PEQ)=360°﹣(115°+130°)=115°;
(3)140°,如图3,延长PF交CD与点M,
∵PF平分∠BPE,QH平分∠EQD,
∴∠1=∠2,∠3=∠4,
∵AB∥CD,
∴∠BPE=∠DNE,∠2=∠PMC=∠1,
又∵∠DQE=∠DNE+∠E,即2∠4=2∠1+80°,
∴∠4﹣∠1=40°,
∴∠PFQ=∠FQD+∠PMC=180°﹣∠4+∠1=180°﹣(∠4﹣∠1)=180°﹣40°=140°.
