2023-2024学年福建省福州市仓山区时代中学九年级(下)开门考数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年福建省福州市仓山区时代中学九年级(下)开门考数学试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 710.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 22:14:44 | ||
图片预览




文档简介
2023-2024学年福建省福州市仓山区时代中学九年级(下)开门考数学试卷
一.选择题(共10小题,每小题4分)
1.(4分)下列图形中,既是中心对称图形,又是轴对称图形的是( )
A. B.
C. D.
2.(4分)习近平总书记提出精准扶贫战略以来,各地积极推进精准扶贫,加大帮扶力度,全国脱贫人口数不断增加,脱贫人口接近11000000人,将数据11000000用科学记数法表示为( )
A.1.1×106 B.1.1×107 C.1.1×108 D.1.1×109
3.(4分)下列各式中,计算正确的是( )
A.a3 a2=a6 B.a3+a2=a5 C.a6÷a3=a2 D.(a3)2=a6
4.(4分)若点A(﹣3,a),B(﹣1,b),C(2,c)在反比例函数的图象上,则a,b,c的大小关系是( )
A.c>b>a B.c>a>b C.a>b>c D.b>c>a
5.(4分)第三届“一带一路”国际高峰论坛在北京成功召开,大会回顾了10年来共建“一带一路”取得的丰硕成果.根据有关数据统计显示,2020年中欧贸易总额约为5800亿欧元,2022年中欧贸易总额约为8600亿欧元,设这两年中欧贸易总额的年平均增长率为x,则可列方程为( )
A.5800(1+x2)=8600 B.5800(1+x)2=8600
C.8600(1﹣x2)=5800 D.8600(1﹣x)2=5800
6.(4分)已知二次函数y=﹣2(x﹣1)2﹣3,下列说法正确的是( )
A.对称轴为直线x=﹣1 B.函数的最大值是3
C.抛物线开口向上 D.顶点坐标为(1,﹣3)
7.(4分)如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠A的度数为( )
A.70° B.75° C.60° D.65°
8.(4分)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AD:DB=2:3,AC=15,则CE=( )
A.4.5 B.6 C.8 D.9
9.(4分)如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于( )
A.20° B.25° C.30° D.32.5°
10.(4分)若点A(﹣1,y1)、B(5,y2)、C(m,y3)在抛物线y=ax2﹣2ax+c上,且y2<y3<y1,则m的取值范围是( )
A.﹣1<m<1 B.m<﹣3或m>1
C.3<m<5或﹣3<m<﹣1 D.﹣5<m<﹣3或﹣1<m<1
二.填空题(共6小题,每小题4分)
11.(4分)使有意义的x的取值范围是 .
12.(4分)在一个不透明的袋子里装有红球和白球共30个,这些球除颜色外都相同,小明通过多次试验发现,摸出白球的频率稳定在0.3左右,则袋子里白球可能是 个.
13.(4分)在平面直角坐标系中,将函数y=2(x﹣1)2的图象先向右平移1个单位长度,再向下平移3个单位长度,所得图象的函数解析式为 .
14.(4分)小明同学利用如图所示的电路探究电流I与电阻R的关系.已知电源电压保持不变,实验用到的电阻阻值和测得的电流如表所示:
电阻R(单位:Ω) 5 10 15 20 25
电流I(单位:A) 1.2 0.6 0.4 0.3 0.24
实验结束后,小明同学发现电流I和电阻R之间是一种数学函数模型,请写出I和R之间函数关系式: .
15.(4分)抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC,BD分别与⊙O相切于点C,D,延长AC,BD交于点P.若∠P=120°,⊙O的半径为6cm,则图中的长为 cm.(结果保留π)
16.(4分)在△ABC中,AB=AC,∠ABC=60°,M是边BC上的一点.,以AM为边作等边△AMN,连接CN.若,则AB= .
三.解答题(共9小题)
17.(8分)计算:()﹣1﹣|﹣3|+2cos30°.
18.(8分)先化简,再求值:(1﹣)÷,其中a=2+.
19.(8分)将数,,分别写在三张相同的不透明卡片上的正面,将卡片洗匀后背面朝上置于桌面,甲乙两个同学从中随机各抽取一张卡片(注:第一个同学抽取到的卡片不放回).
(1)甲同学抽到的卡片上数字是的概率是 ;
(2)请用列举法求甲乙两个同学抽到的卡片数字都是无理数的概率.
20.(8分)在抗击新冠肺炎疫情期间,某社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精200瓶,消毒液300瓶,花费2600元;第二次购买酒精100瓶,消毒液200瓶,花费1500元.
(1)求酒精和消毒液的价格.
(2)若按照酒精和消毒液的原价再一次购买,根据需要,购买的酒精数量是消毒液数量的2倍,现有购买资金2000元,则最多能购买消毒液多少瓶?
21.(8分)已知,如图,△ABC的顶点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°.
(1)若⊙O半径为3,求弦CD的长;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
22.(10分)已知二次函数y=ax2+bx+c中的x,y满足如表;
x … 0 1 m 3 4 …
y … n 1.5 2 1.5 0 …
(1)补全表格,m= ,n= ;
(2)利用上表,在平面直角坐标系中画出这条抛物线的图象;
(3)当a≤x≤4时,y的取值范围为0≤y≤2,则a的取值范围为 .
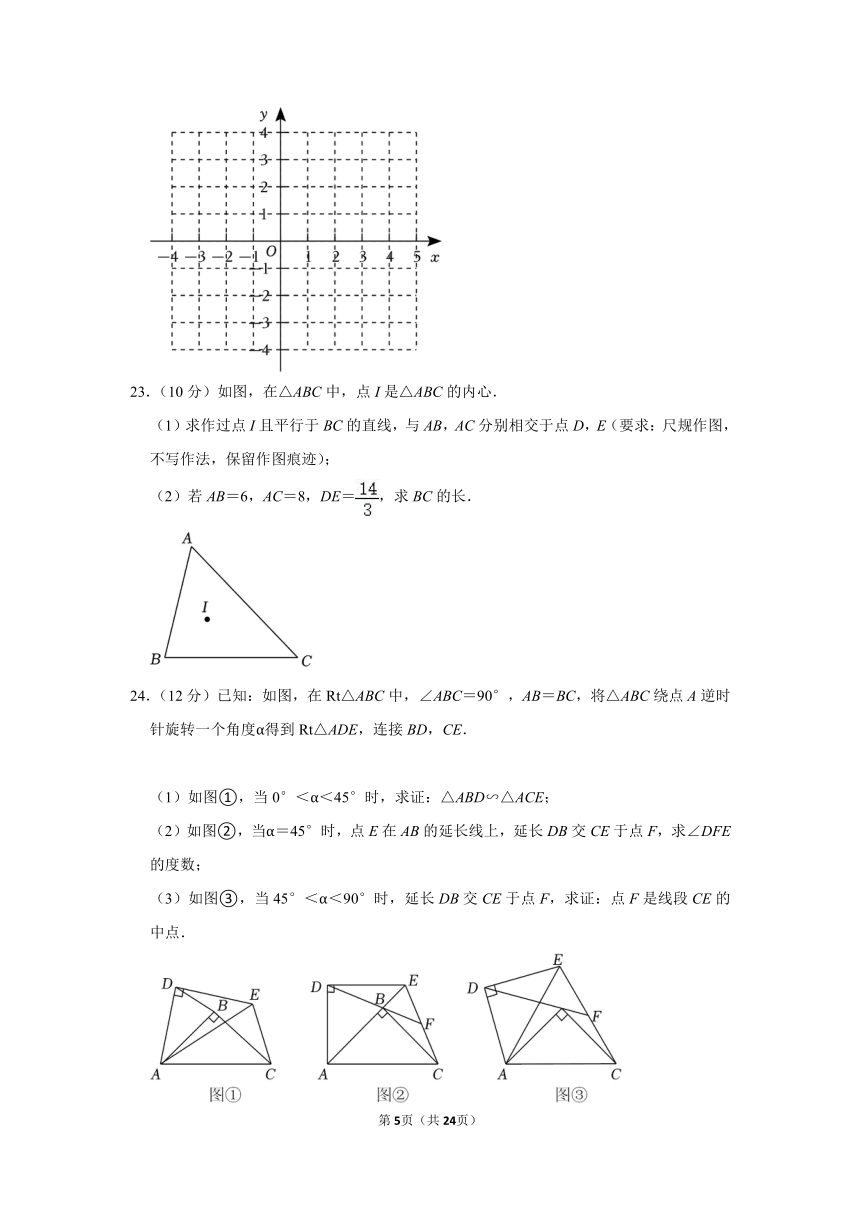
23.(10分)如图,在△ABC中,点I是△ABC的内心.
(1)求作过点I且平行于BC的直线,与AB,AC分别相交于点D,E(要求:尺规作图,不写作法,保留作图痕迹);
(2)若AB=6,AC=8,DE=,求BC的长.
24.(12分)已知:如图,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针旋转一个角度α得到Rt△ADE,连接BD,CE.
(1)如图①,当0°<α<45°时,求证:△ABD∽△ACE;
(2)如图②,当α=45°时,点E在AB的延长线上,延长DB交CE于点F,求∠DFE的度数;
(3)如图③,当45°<α<90°时,延长DB交CE于点F,求证:点F是线段CE的中点.
25.(14分)如图,在平面直角坐标系中,抛物线y=x2+bx+c交x轴于A(﹣1,0),B(3,0)两点,交y轴于点C.
(1)求二次函数解析式;
(2)如图1,若在x轴上方的抛物线上存在一点D,使得∠ACD=45°,求点D的坐标;
(3)如图2,平面上一点E(3,2),过点E作任意一条直线交抛物线于P、Q两点,连接AP、AQ,分别交y轴于M、N两点,则OM与ON的积是否为定值?若是,求出此定值;若不是,请说明理由.
参考答案与解析
一.选择题(共10小题,每小题4分)
1.(4分)下列图形中,既是中心对称图形,又是轴对称图形的是( )
A. B.
C. D.
【解答】解:A、是轴对称图形,不是中心对称图形,不符合题意;
B、是轴对称图形,不是中心对称图形,不符合题意;
C、既是轴对称图形,也是中心对称图形,符合题意;
D、不是轴对称图形,是中心对称图形,不符合题意.
故选:C.
2.(4分)习近平总书记提出精准扶贫战略以来,各地积极推进精准扶贫,加大帮扶力度,全国脱贫人口数不断增加,脱贫人口接近11000000人,将数据11000000用科学记数法表示为( )
A.1.1×106 B.1.1×107 C.1.1×108 D.1.1×109
【解答】解:将11000000用科学记数法表示为1.1×107.
故选:B.
3.(4分)下列各式中,计算正确的是( )
A.a3 a2=a6 B.a3+a2=a5 C.a6÷a3=a2 D.(a3)2=a6
【解答】解:A、a3 a2=a5,错误;
B、a3+a2不能合并,错误;
C、a6÷a3=a3,错误;
D、(a3)2=a6,正确;
故选:D.
4.(4分)若点A(﹣3,a),B(﹣1,b),C(2,c)在反比例函数的图象上,则a,b,c的大小关系是( )
A.c>b>a B.c>a>b C.a>b>c D.b>c>a
【解答】解:在反比例函数中,k=1>0,图象分布在第一三象限,在每个象限内,y随x的增大而减小,
∵C(2,c)在第一象限,
∴c>0,
∵A(﹣3,a),B(﹣1,b)在第三象限,且x<0时,y随x的增大而减小,﹣3<﹣1,
∴0>a>b,
∴c>a>b,
故选:B.
5.(4分)第三届“一带一路”国际高峰论坛在北京成功召开,大会回顾了10年来共建“一带一路”取得的丰硕成果.根据有关数据统计显示,2020年中欧贸易总额约为5800亿欧元,2022年中欧贸易总额约为8600亿欧元,设这两年中欧贸易总额的年平均增长率为x,则可列方程为( )
A.5800(1+x2)=8600 B.5800(1+x)2=8600
C.8600(1﹣x2)=5800 D.8600(1﹣x)2=5800
【解答】解:由题意得,5800(1+x)2=8600,
故选:B.
6.(4分)已知二次函数y=﹣2(x﹣1)2﹣3,下列说法正确的是( )
A.对称轴为直线x=﹣1 B.函数的最大值是3
C.抛物线开口向上 D.顶点坐标为(1,﹣3)
【解答】解:由题意,∵二次函数y=﹣2(x﹣1)2﹣3的开口向下,对称轴是直线x=1,
∴当x=1时,函数有最大值为﹣3;顶点坐标为(1,﹣3).
故选:D.
7.(4分)如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠A的度数为( )
A.70° B.75° C.60° D.65°
【解答】解:由题意得∠AOD=30°、OA=OD,
∴∠A=∠ADO==75°,
故选:B.
8.(4分)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AD:DB=2:3,AC=15,则CE=( )
A.4.5 B.6 C.8 D.9
【解答】解:∵AD:DB=2:3,
∴BD:AB=3:5,
∵DE∥CB,
∴==,
∵AC=15,
∴EC=9.
故选:D.
9.(4分)如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于( )
A.20° B.25° C.30° D.32.5°
【解答】解:连接OD,
∵OC⊥AB,
∴∠COB=90°,
∵∠AEC=65°,
∴∠OCE=180°﹣90°﹣65°=25°,
∵OD=OC,
∴∠ODC=∠OCD=25°,
∴∠DOC=180°﹣25°﹣25°=130°,
∴∠DOB=∠DOC﹣∠BOC=130°﹣90°=40°,
∴由圆周角定理得:∠BAD=∠DOB=20°,
故选:A.
10.(4分)若点A(﹣1,y1)、B(5,y2)、C(m,y3)在抛物线y=ax2﹣2ax+c上,且y2<y3<y1,则m的取值范围是( )
A.﹣1<m<1 B.m<﹣3或m>1
C.3<m<5或﹣3<m<﹣1 D.﹣5<m<﹣3或﹣1<m<1
【解答】解:抛物线y=ax2﹣2ax+c的对称轴为直线,
∵A(﹣1,y1)、B(5,y2)、C(m,y3)在抛物线y=ax2﹣2ax+c上,
∴根据抛物线对称性可知:
点A(﹣1,y1)与点A'(3,y1)关于对称轴直线x=1对称,
点B(5,y2)与点B'(﹣3,y2)关于对称轴直线x=1对称,
∵y2<y1,﹣3<﹣1,3<5,
∴当x<1时,函数值y随着x的增大而增大;当x>1时,函数值y随着x的增大而减小;
∴抛物线y=ax2﹣2ax+c的图象开口向下,
作图如下:
由图可知:要满足y2<y3<y1,则m的取值范围为:3<m<5或﹣3<m<﹣1,
故选:C.
二.填空题(共6小题,每小题4分)
11.(4分)使有意义的x的取值范围是 x≥2 .
【解答】解:根据二次根式的意义,得
x﹣2≥0,解得x≥2.
12.(4分)在一个不透明的袋子里装有红球和白球共30个,这些球除颜色外都相同,小明通过多次试验发现,摸出白球的频率稳定在0.3左右,则袋子里白球可能是 9 个.
【解答】解:由题意可得,
30×0.3=9(个),
即袋子中白球的个数最有可能是9个,
故答案为:9.
13.(4分)在平面直角坐标系中,将函数y=2(x﹣1)2的图象先向右平移1个单位长度,再向下平移3个单位长度,所得图象的函数解析式为 y=2(x﹣2)2﹣3 .
【解答】解:将函数y=2(x﹣1)2的图象先向右平移1个单位长度,再向下平移3个单位长度,所得图象的函数解析式为:y=2(x﹣1﹣1)2﹣3,即y=2(x﹣2)2﹣3.
故答案为:y=2(x﹣2)2﹣3.
14.(4分)小明同学利用如图所示的电路探究电流I与电阻R的关系.已知电源电压保持不变,实验用到的电阻阻值和测得的电流如表所示:
电阻R(单位:Ω) 5 10 15 20 25
电流I(单位:A) 1.2 0.6 0.4 0.3 0.24
实验结束后,小明同学发现电流I和电阻R之间是一种数学函数模型,请写出I和R之间函数关系式: I= .
【解答】解:由表格中数据可得:U=5×1.2=10×0.6=6,
则I==.
故答案为:I=.
15.(4分)抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC,BD分别与⊙O相切于点C,D,延长AC,BD交于点P.若∠P=120°,⊙O的半径为6cm,则图中的长为 2π cm.(结果保留π)
【解答】解:如图所示,连接OC,OD,
∵AC,BD分别与⊙O相切于点C,D,
∴∠OCP=∠ODP=90°,
由四边形内角和为360°可得,
∠COD=360°﹣∠OCP﹣∠ODP﹣∠CPD
=360°﹣90°﹣90°﹣120°
=60°.
∴的长==2π.
故答案为:2π.
16.(4分)在△ABC中,AB=AC,∠ABC=60°,M是边BC上的一点.,以AM为边作等边△AMN,连接CN.若,则AB= 或3 .
【解答】解:当N在AM右侧时,如图,
在△ABC中,AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∵△AMN是等边三角形,
∴∠BAM+∠CAM=∠CAN+∠CAM=60°,
∴∠BAM=∠CAN,
∵AB=AC,AM=AN,
∴△BAM≌△CAN(SAS),
∴,
∵,
∴,
∴,
∴;
当N在AM右左侧时,过N作ND⊥BC于D,
同上易证△BAN≌△CAM(SAS),
∴,∠ABN=∠ACM=∠ABC=60°,
∴∠NBD=60°,
∵ND⊥BC,
∴∠BND=30°,
∴,
∴,
∴,
∵DN2+CD2=CN2,
∵,
解得:BC=3,
∴AB=BC=3,
故答案为:或3.
三.解答题(共9小题)
17.(8分)计算:()﹣1﹣|﹣3|+2cos30°.
【解答】解:原式=2﹣(3﹣)+2×
=2﹣3++
=2﹣1.
18.(8分)先化简,再求值:(1﹣)÷,其中a=2+.
【解答】解:(1﹣)÷
=
=
=,
当a=2+时,原式==.
19.(8分)将数,,分别写在三张相同的不透明卡片上的正面,将卡片洗匀后背面朝上置于桌面,甲乙两个同学从中随机各抽取一张卡片(注:第一个同学抽取到的卡片不放回).
(1)甲同学抽到的卡片上数字是的概率是 ;
(2)请用列举法求甲乙两个同学抽到的卡片数字都是无理数的概率.
【解答】解:(1)∵有3张卡片,其中只有一张卡片上的数字是,
∴P(甲同学抽到的卡片上数字是)=,
故答案为:;
(2)画树状图如下:
∵一共有6种等可能的结果,其中甲乙两个同学抽到的卡片数字都是无理数有2种可能,
∴P(甲乙两个同学抽到的卡片数字都是无理数)=.
20.(8分)在抗击新冠肺炎疫情期间,某社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精200瓶,消毒液300瓶,花费2600元;第二次购买酒精100瓶,消毒液200瓶,花费1500元.
(1)求酒精和消毒液的价格.
(2)若按照酒精和消毒液的原价再一次购买,根据需要,购买的酒精数量是消毒液数量的2倍,现有购买资金2000元,则最多能购买消毒液多少瓶?
【解答】解:(1)设酒精x元/瓶,消毒液y元/瓶,
依题意得:,
解得:.
答:酒精7元/瓶,消毒液4元/瓶.
(2)设购买消毒液m瓶,则购买酒精2m瓶,
依题意得:7×2m+4m≤2000,
解得:m≤.
又∵m为正整数,
∴m可以取的最大值111.
答:最多能购买消毒液111瓶.
21.(8分)已知,如图,△ABC的顶点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°.
(1)若⊙O半径为3,求弦CD的长;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
【解答】(1)解:连接OC、OD,如图1所示:
则OC=OD=3,
∵∠A=30°,
∴∠DOC=60°,
∴△OCD是等边三角形,
∴CD=3;
(2)证明:解法一:连接CO并延长交⊙O于点M,连AM,如图2所示:
则∠MAC=90°,∠M+∠ADC=180°,
∴∠M+∠ACM=90°,
∵∠ACB+∠ADC=180°,
∴∠M=∠ACB,
∴∠ACB+∠ACM=90°,
即∠BCM=90°,且CM是⊙O的直径,
∴BC是⊙O的切线;
解法二:如图1,
∵∠ACB+∠ADC=180°,∠ADC+∠BDC=180°,
∴∠ACB=∠BDC,
∵∠BDC=∠A+∠ACD,∠ACB=∠ACD+∠BCD,
∴∠BCD=∠A=30°,
∵△OCD是等边三角形,
∴∠OCD=60°,
∴∠OCB=∠OCD+∠BCD=60°+30°=90°,且OC是⊙O的半径,
∴BC是⊙O的切线.
22.(10分)已知二次函数y=ax2+bx+c中的x,y满足如表;
x … 0 1 m 3 4 …
y … n 1.5 2 1.5 0 …
(1)补全表格,m= 2 ,n= 0 ;
(2)利用上表,在平面直角坐标系中画出这条抛物线的图象;
(3)当a≤x≤4时,y的取值范围为0≤y≤2,则a的取值范围为 0≤a≤2 .
【解答】解:(1)根据表格数据和函数的对称性可知,函数的对称轴是直线x=2,
点(0,0)和点(4,0)关于对称轴对称,
∴n=0,
设二次函数y=ax(x﹣4),
代入(1,1.5)得1.5=﹣3a,
∴a=﹣,
∴y=﹣x(x﹣4),
当y=2时,2=﹣,
解得x=2,
∴m=2,
故答案为:2,0;
(2)画出这条抛物线的图象如图:
;
(3)观察图象,当x=2时,函数y=2,当x=0或x=4时,y=0,
∵当a≤x≤4时,y的取值范围为0≤y≤2,
∴0≤a≤2,
故答案为:0≤a≤2.
23.(10分)如图,在△ABC中,点I是△ABC的内心.
(1)求作过点I且平行于BC的直线,与AB,AC分别相交于点D,E(要求:尺规作图,不写作法,保留作图痕迹);
(2)若AB=6,AC=8,DE=,求BC的长.
【解答】解:(1)如图,连接BI,作∠DIB=∠IBC,直线ID交AC于E点,
则直线DE为所作;
(2)连接CI,如图,
∵点I是△ABC的内心,
∴BI平分∠ABC,CI平分∠ACB,
∴∠DBI=∠CBI,∠ECI=∠BCI,
∵DE∥BC,
∴∠DIB=∠CBI,∠EIC=∠BCI,
∴∠DIB=∠DBI,∠EIC=∠ECI,
∴DB=DI,EI=EC,
设BD=x,则DI=x,CE=EI=﹣﹣x,
∵DE∥BC,
∴BD:BA=CE:CA,
即x:6=(﹣x):8,
解得x=2,
∴AD=AB﹣BD=4,
∵DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=AD:AB,即:BC=4:6,
解得BC=7,
即BC的长为7.
24.(12分)已知:如图,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针旋转一个角度α得到Rt△ADE,连接BD,CE.
(1)如图①,当0°<α<45°时,求证:△ABD∽△ACE;
(2)如图②,当α=45°时,点E在AB的延长线上,延长DB交CE于点F,求∠DFE的度数;
(3)如图③,当45°<α<90°时,延长DB交CE于点F,求证:点F是线段CE的中点.
【解答】(1)证明:∵将△ABC绕点A逆时针旋一个角度α得到Rt△ADE,
∴AD=AB,AE=AC,∠BAD=∠CAE,
∴,
∴△ABD∽△ACE;
(2)解:如图,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠BAC=∠BCA=45°,
由旋转的性质可知:AD=AB,AE=AC,∠DAE=∠BAC=45°,
∴∠1=∠2=67.5°,∠3=∠ACE=67.5°,
∴∠2=∠4=67.5°,
∴∠BFE=180°﹣∠3﹣∠4=45°;
(3)证明:如图,过点E作EM⊥DF于点M,过点C作CN⊥DF,交DF的延长线于点N,
∴∠DME=∠EMF=∠BNC=90°,
由旋转的性质可知:DE=BC,AD=AB,∠ADE=∠ABC=90°,
∴∠1=∠2,∠1+∠4=90°,∠2+∠3=180°﹣∠ABC=90°,
∴∠3=∠4,
∴△DEM≌△BCN(AAS),
∴EM=CN,
又∵∠5=∠6,∠EMF=∠CNF=90°,
∴△FEM≌△FCN(AAS),
∴EF=CF,
即F是CE的中点.
25.(14分)如图,在平面直角坐标系中,抛物线y=x2+bx+c交x轴于A(﹣1,0),B(3,0)两点,交y轴于点C.
(1)求二次函数解析式;
(2)如图1,若在x轴上方的抛物线上存在一点D,使得∠ACD=45°,求点D的坐标;
(3)如图2,平面上一点E(3,2),过点E作任意一条直线交抛物线于P、Q两点,连接AP、AQ,分别交y轴于M、N两点,则OM与ON的积是否为定值?若是,求出此定值;若不是,请说明理由.
【解答】解:(1)设y=a(x﹣x1)(x﹣x2),
则y=(x﹣3)(x+1)=x2﹣2x﹣3;
(2)抛物线的表达式为y=x2﹣2x﹣3,则点C(0,﹣3),
过A作AK⊥AC交CD于点K,作KH⊥x轴于点H,如图1,
∵∠ACD=45°,
∴△CAK是等腰直角三角形,
∴AC=AK,
∵∠AOC=∠KHA=90°,∠ACO=90°﹣∠OAC=∠KAH,
∴△OAC≌△HKA(AAS),
∴AH=CO=3,KH=OA=1,
∴K(2,1),
设直线CD的解析式为y=kx﹣3,
∴2k﹣3=1,
∴k=2,
∴直线CD的解析式为y=2x﹣3,
联立,
解得x=0(舍去),或x=4,
∴D(4,5);
(3)OM与ON的积是定值,理由如下:
∵过点E(3,2)作一直线交抛物线于P、Q两点,
设直线PQ的解析式为y=ax+b,P(x1,y1),Q(x2,y2),
∴2=3a+b,b=2﹣3a,
∴直线PQ的解析式为y=ax+2﹣3a②,
联立①②得:x2+(1﹣3﹣a)x+3a﹣5=0,
∴x1+x2=a+2,x1 x2=3a﹣5,
如图2,作PS⊥x轴于点S,作QT⊥x轴于点T,
则△AMO∽△APS,
∴=,
即=,
∴OM=x1﹣3,
同理,ON=﹣(x2﹣3),
∴OM ON=﹣(x1﹣3)(x2﹣3)=﹣[x1 x2﹣3(x1+x2)+9]=﹣[3a﹣5﹣3(a+2)+9]=2,为定值.
第1页(共1页)
一.选择题(共10小题,每小题4分)
1.(4分)下列图形中,既是中心对称图形,又是轴对称图形的是( )
A. B.
C. D.
2.(4分)习近平总书记提出精准扶贫战略以来,各地积极推进精准扶贫,加大帮扶力度,全国脱贫人口数不断增加,脱贫人口接近11000000人,将数据11000000用科学记数法表示为( )
A.1.1×106 B.1.1×107 C.1.1×108 D.1.1×109
3.(4分)下列各式中,计算正确的是( )
A.a3 a2=a6 B.a3+a2=a5 C.a6÷a3=a2 D.(a3)2=a6
4.(4分)若点A(﹣3,a),B(﹣1,b),C(2,c)在反比例函数的图象上,则a,b,c的大小关系是( )
A.c>b>a B.c>a>b C.a>b>c D.b>c>a
5.(4分)第三届“一带一路”国际高峰论坛在北京成功召开,大会回顾了10年来共建“一带一路”取得的丰硕成果.根据有关数据统计显示,2020年中欧贸易总额约为5800亿欧元,2022年中欧贸易总额约为8600亿欧元,设这两年中欧贸易总额的年平均增长率为x,则可列方程为( )
A.5800(1+x2)=8600 B.5800(1+x)2=8600
C.8600(1﹣x2)=5800 D.8600(1﹣x)2=5800
6.(4分)已知二次函数y=﹣2(x﹣1)2﹣3,下列说法正确的是( )
A.对称轴为直线x=﹣1 B.函数的最大值是3
C.抛物线开口向上 D.顶点坐标为(1,﹣3)
7.(4分)如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠A的度数为( )
A.70° B.75° C.60° D.65°
8.(4分)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AD:DB=2:3,AC=15,则CE=( )
A.4.5 B.6 C.8 D.9
9.(4分)如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于( )
A.20° B.25° C.30° D.32.5°
10.(4分)若点A(﹣1,y1)、B(5,y2)、C(m,y3)在抛物线y=ax2﹣2ax+c上,且y2<y3<y1,则m的取值范围是( )
A.﹣1<m<1 B.m<﹣3或m>1
C.3<m<5或﹣3<m<﹣1 D.﹣5<m<﹣3或﹣1<m<1
二.填空题(共6小题,每小题4分)
11.(4分)使有意义的x的取值范围是 .
12.(4分)在一个不透明的袋子里装有红球和白球共30个,这些球除颜色外都相同,小明通过多次试验发现,摸出白球的频率稳定在0.3左右,则袋子里白球可能是 个.
13.(4分)在平面直角坐标系中,将函数y=2(x﹣1)2的图象先向右平移1个单位长度,再向下平移3个单位长度,所得图象的函数解析式为 .
14.(4分)小明同学利用如图所示的电路探究电流I与电阻R的关系.已知电源电压保持不变,实验用到的电阻阻值和测得的电流如表所示:
电阻R(单位:Ω) 5 10 15 20 25
电流I(单位:A) 1.2 0.6 0.4 0.3 0.24
实验结束后,小明同学发现电流I和电阻R之间是一种数学函数模型,请写出I和R之间函数关系式: .
15.(4分)抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC,BD分别与⊙O相切于点C,D,延长AC,BD交于点P.若∠P=120°,⊙O的半径为6cm,则图中的长为 cm.(结果保留π)
16.(4分)在△ABC中,AB=AC,∠ABC=60°,M是边BC上的一点.,以AM为边作等边△AMN,连接CN.若,则AB= .
三.解答题(共9小题)
17.(8分)计算:()﹣1﹣|﹣3|+2cos30°.
18.(8分)先化简,再求值:(1﹣)÷,其中a=2+.
19.(8分)将数,,分别写在三张相同的不透明卡片上的正面,将卡片洗匀后背面朝上置于桌面,甲乙两个同学从中随机各抽取一张卡片(注:第一个同学抽取到的卡片不放回).
(1)甲同学抽到的卡片上数字是的概率是 ;
(2)请用列举法求甲乙两个同学抽到的卡片数字都是无理数的概率.
20.(8分)在抗击新冠肺炎疫情期间,某社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精200瓶,消毒液300瓶,花费2600元;第二次购买酒精100瓶,消毒液200瓶,花费1500元.
(1)求酒精和消毒液的价格.
(2)若按照酒精和消毒液的原价再一次购买,根据需要,购买的酒精数量是消毒液数量的2倍,现有购买资金2000元,则最多能购买消毒液多少瓶?
21.(8分)已知,如图,△ABC的顶点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°.
(1)若⊙O半径为3,求弦CD的长;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
22.(10分)已知二次函数y=ax2+bx+c中的x,y满足如表;
x … 0 1 m 3 4 …
y … n 1.5 2 1.5 0 …
(1)补全表格,m= ,n= ;
(2)利用上表,在平面直角坐标系中画出这条抛物线的图象;
(3)当a≤x≤4时,y的取值范围为0≤y≤2,则a的取值范围为 .
23.(10分)如图,在△ABC中,点I是△ABC的内心.
(1)求作过点I且平行于BC的直线,与AB,AC分别相交于点D,E(要求:尺规作图,不写作法,保留作图痕迹);
(2)若AB=6,AC=8,DE=,求BC的长.
24.(12分)已知:如图,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针旋转一个角度α得到Rt△ADE,连接BD,CE.
(1)如图①,当0°<α<45°时,求证:△ABD∽△ACE;
(2)如图②,当α=45°时,点E在AB的延长线上,延长DB交CE于点F,求∠DFE的度数;
(3)如图③,当45°<α<90°时,延长DB交CE于点F,求证:点F是线段CE的中点.
25.(14分)如图,在平面直角坐标系中,抛物线y=x2+bx+c交x轴于A(﹣1,0),B(3,0)两点,交y轴于点C.
(1)求二次函数解析式;
(2)如图1,若在x轴上方的抛物线上存在一点D,使得∠ACD=45°,求点D的坐标;
(3)如图2,平面上一点E(3,2),过点E作任意一条直线交抛物线于P、Q两点,连接AP、AQ,分别交y轴于M、N两点,则OM与ON的积是否为定值?若是,求出此定值;若不是,请说明理由.
参考答案与解析
一.选择题(共10小题,每小题4分)
1.(4分)下列图形中,既是中心对称图形,又是轴对称图形的是( )
A. B.
C. D.
【解答】解:A、是轴对称图形,不是中心对称图形,不符合题意;
B、是轴对称图形,不是中心对称图形,不符合题意;
C、既是轴对称图形,也是中心对称图形,符合题意;
D、不是轴对称图形,是中心对称图形,不符合题意.
故选:C.
2.(4分)习近平总书记提出精准扶贫战略以来,各地积极推进精准扶贫,加大帮扶力度,全国脱贫人口数不断增加,脱贫人口接近11000000人,将数据11000000用科学记数法表示为( )
A.1.1×106 B.1.1×107 C.1.1×108 D.1.1×109
【解答】解:将11000000用科学记数法表示为1.1×107.
故选:B.
3.(4分)下列各式中,计算正确的是( )
A.a3 a2=a6 B.a3+a2=a5 C.a6÷a3=a2 D.(a3)2=a6
【解答】解:A、a3 a2=a5,错误;
B、a3+a2不能合并,错误;
C、a6÷a3=a3,错误;
D、(a3)2=a6,正确;
故选:D.
4.(4分)若点A(﹣3,a),B(﹣1,b),C(2,c)在反比例函数的图象上,则a,b,c的大小关系是( )
A.c>b>a B.c>a>b C.a>b>c D.b>c>a
【解答】解:在反比例函数中,k=1>0,图象分布在第一三象限,在每个象限内,y随x的增大而减小,
∵C(2,c)在第一象限,
∴c>0,
∵A(﹣3,a),B(﹣1,b)在第三象限,且x<0时,y随x的增大而减小,﹣3<﹣1,
∴0>a>b,
∴c>a>b,
故选:B.
5.(4分)第三届“一带一路”国际高峰论坛在北京成功召开,大会回顾了10年来共建“一带一路”取得的丰硕成果.根据有关数据统计显示,2020年中欧贸易总额约为5800亿欧元,2022年中欧贸易总额约为8600亿欧元,设这两年中欧贸易总额的年平均增长率为x,则可列方程为( )
A.5800(1+x2)=8600 B.5800(1+x)2=8600
C.8600(1﹣x2)=5800 D.8600(1﹣x)2=5800
【解答】解:由题意得,5800(1+x)2=8600,
故选:B.
6.(4分)已知二次函数y=﹣2(x﹣1)2﹣3,下列说法正确的是( )
A.对称轴为直线x=﹣1 B.函数的最大值是3
C.抛物线开口向上 D.顶点坐标为(1,﹣3)
【解答】解:由题意,∵二次函数y=﹣2(x﹣1)2﹣3的开口向下,对称轴是直线x=1,
∴当x=1时,函数有最大值为﹣3;顶点坐标为(1,﹣3).
故选:D.
7.(4分)如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠A的度数为( )
A.70° B.75° C.60° D.65°
【解答】解:由题意得∠AOD=30°、OA=OD,
∴∠A=∠ADO==75°,
故选:B.
8.(4分)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AD:DB=2:3,AC=15,则CE=( )
A.4.5 B.6 C.8 D.9
【解答】解:∵AD:DB=2:3,
∴BD:AB=3:5,
∵DE∥CB,
∴==,
∵AC=15,
∴EC=9.
故选:D.
9.(4分)如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于( )
A.20° B.25° C.30° D.32.5°
【解答】解:连接OD,
∵OC⊥AB,
∴∠COB=90°,
∵∠AEC=65°,
∴∠OCE=180°﹣90°﹣65°=25°,
∵OD=OC,
∴∠ODC=∠OCD=25°,
∴∠DOC=180°﹣25°﹣25°=130°,
∴∠DOB=∠DOC﹣∠BOC=130°﹣90°=40°,
∴由圆周角定理得:∠BAD=∠DOB=20°,
故选:A.
10.(4分)若点A(﹣1,y1)、B(5,y2)、C(m,y3)在抛物线y=ax2﹣2ax+c上,且y2<y3<y1,则m的取值范围是( )
A.﹣1<m<1 B.m<﹣3或m>1
C.3<m<5或﹣3<m<﹣1 D.﹣5<m<﹣3或﹣1<m<1
【解答】解:抛物线y=ax2﹣2ax+c的对称轴为直线,
∵A(﹣1,y1)、B(5,y2)、C(m,y3)在抛物线y=ax2﹣2ax+c上,
∴根据抛物线对称性可知:
点A(﹣1,y1)与点A'(3,y1)关于对称轴直线x=1对称,
点B(5,y2)与点B'(﹣3,y2)关于对称轴直线x=1对称,
∵y2<y1,﹣3<﹣1,3<5,
∴当x<1时,函数值y随着x的增大而增大;当x>1时,函数值y随着x的增大而减小;
∴抛物线y=ax2﹣2ax+c的图象开口向下,
作图如下:
由图可知:要满足y2<y3<y1,则m的取值范围为:3<m<5或﹣3<m<﹣1,
故选:C.
二.填空题(共6小题,每小题4分)
11.(4分)使有意义的x的取值范围是 x≥2 .
【解答】解:根据二次根式的意义,得
x﹣2≥0,解得x≥2.
12.(4分)在一个不透明的袋子里装有红球和白球共30个,这些球除颜色外都相同,小明通过多次试验发现,摸出白球的频率稳定在0.3左右,则袋子里白球可能是 9 个.
【解答】解:由题意可得,
30×0.3=9(个),
即袋子中白球的个数最有可能是9个,
故答案为:9.
13.(4分)在平面直角坐标系中,将函数y=2(x﹣1)2的图象先向右平移1个单位长度,再向下平移3个单位长度,所得图象的函数解析式为 y=2(x﹣2)2﹣3 .
【解答】解:将函数y=2(x﹣1)2的图象先向右平移1个单位长度,再向下平移3个单位长度,所得图象的函数解析式为:y=2(x﹣1﹣1)2﹣3,即y=2(x﹣2)2﹣3.
故答案为:y=2(x﹣2)2﹣3.
14.(4分)小明同学利用如图所示的电路探究电流I与电阻R的关系.已知电源电压保持不变,实验用到的电阻阻值和测得的电流如表所示:
电阻R(单位:Ω) 5 10 15 20 25
电流I(单位:A) 1.2 0.6 0.4 0.3 0.24
实验结束后,小明同学发现电流I和电阻R之间是一种数学函数模型,请写出I和R之间函数关系式: I= .
【解答】解:由表格中数据可得:U=5×1.2=10×0.6=6,
则I==.
故答案为:I=.
15.(4分)抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC,BD分别与⊙O相切于点C,D,延长AC,BD交于点P.若∠P=120°,⊙O的半径为6cm,则图中的长为 2π cm.(结果保留π)
【解答】解:如图所示,连接OC,OD,
∵AC,BD分别与⊙O相切于点C,D,
∴∠OCP=∠ODP=90°,
由四边形内角和为360°可得,
∠COD=360°﹣∠OCP﹣∠ODP﹣∠CPD
=360°﹣90°﹣90°﹣120°
=60°.
∴的长==2π.
故答案为:2π.
16.(4分)在△ABC中,AB=AC,∠ABC=60°,M是边BC上的一点.,以AM为边作等边△AMN,连接CN.若,则AB= 或3 .
【解答】解:当N在AM右侧时,如图,
在△ABC中,AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∵△AMN是等边三角形,
∴∠BAM+∠CAM=∠CAN+∠CAM=60°,
∴∠BAM=∠CAN,
∵AB=AC,AM=AN,
∴△BAM≌△CAN(SAS),
∴,
∵,
∴,
∴,
∴;
当N在AM右左侧时,过N作ND⊥BC于D,
同上易证△BAN≌△CAM(SAS),
∴,∠ABN=∠ACM=∠ABC=60°,
∴∠NBD=60°,
∵ND⊥BC,
∴∠BND=30°,
∴,
∴,
∴,
∵DN2+CD2=CN2,
∵,
解得:BC=3,
∴AB=BC=3,
故答案为:或3.
三.解答题(共9小题)
17.(8分)计算:()﹣1﹣|﹣3|+2cos30°.
【解答】解:原式=2﹣(3﹣)+2×
=2﹣3++
=2﹣1.
18.(8分)先化简,再求值:(1﹣)÷,其中a=2+.
【解答】解:(1﹣)÷
=
=
=,
当a=2+时,原式==.
19.(8分)将数,,分别写在三张相同的不透明卡片上的正面,将卡片洗匀后背面朝上置于桌面,甲乙两个同学从中随机各抽取一张卡片(注:第一个同学抽取到的卡片不放回).
(1)甲同学抽到的卡片上数字是的概率是 ;
(2)请用列举法求甲乙两个同学抽到的卡片数字都是无理数的概率.
【解答】解:(1)∵有3张卡片,其中只有一张卡片上的数字是,
∴P(甲同学抽到的卡片上数字是)=,
故答案为:;
(2)画树状图如下:
∵一共有6种等可能的结果,其中甲乙两个同学抽到的卡片数字都是无理数有2种可能,
∴P(甲乙两个同学抽到的卡片数字都是无理数)=.
20.(8分)在抗击新冠肺炎疫情期间,某社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精200瓶,消毒液300瓶,花费2600元;第二次购买酒精100瓶,消毒液200瓶,花费1500元.
(1)求酒精和消毒液的价格.
(2)若按照酒精和消毒液的原价再一次购买,根据需要,购买的酒精数量是消毒液数量的2倍,现有购买资金2000元,则最多能购买消毒液多少瓶?
【解答】解:(1)设酒精x元/瓶,消毒液y元/瓶,
依题意得:,
解得:.
答:酒精7元/瓶,消毒液4元/瓶.
(2)设购买消毒液m瓶,则购买酒精2m瓶,
依题意得:7×2m+4m≤2000,
解得:m≤.
又∵m为正整数,
∴m可以取的最大值111.
答:最多能购买消毒液111瓶.
21.(8分)已知,如图,△ABC的顶点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°.
(1)若⊙O半径为3,求弦CD的长;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
【解答】(1)解:连接OC、OD,如图1所示:
则OC=OD=3,
∵∠A=30°,
∴∠DOC=60°,
∴△OCD是等边三角形,
∴CD=3;
(2)证明:解法一:连接CO并延长交⊙O于点M,连AM,如图2所示:
则∠MAC=90°,∠M+∠ADC=180°,
∴∠M+∠ACM=90°,
∵∠ACB+∠ADC=180°,
∴∠M=∠ACB,
∴∠ACB+∠ACM=90°,
即∠BCM=90°,且CM是⊙O的直径,
∴BC是⊙O的切线;
解法二:如图1,
∵∠ACB+∠ADC=180°,∠ADC+∠BDC=180°,
∴∠ACB=∠BDC,
∵∠BDC=∠A+∠ACD,∠ACB=∠ACD+∠BCD,
∴∠BCD=∠A=30°,
∵△OCD是等边三角形,
∴∠OCD=60°,
∴∠OCB=∠OCD+∠BCD=60°+30°=90°,且OC是⊙O的半径,
∴BC是⊙O的切线.
22.(10分)已知二次函数y=ax2+bx+c中的x,y满足如表;
x … 0 1 m 3 4 …
y … n 1.5 2 1.5 0 …
(1)补全表格,m= 2 ,n= 0 ;
(2)利用上表,在平面直角坐标系中画出这条抛物线的图象;
(3)当a≤x≤4时,y的取值范围为0≤y≤2,则a的取值范围为 0≤a≤2 .
【解答】解:(1)根据表格数据和函数的对称性可知,函数的对称轴是直线x=2,
点(0,0)和点(4,0)关于对称轴对称,
∴n=0,
设二次函数y=ax(x﹣4),
代入(1,1.5)得1.5=﹣3a,
∴a=﹣,
∴y=﹣x(x﹣4),
当y=2时,2=﹣,
解得x=2,
∴m=2,
故答案为:2,0;
(2)画出这条抛物线的图象如图:
;
(3)观察图象,当x=2时,函数y=2,当x=0或x=4时,y=0,
∵当a≤x≤4时,y的取值范围为0≤y≤2,
∴0≤a≤2,
故答案为:0≤a≤2.
23.(10分)如图,在△ABC中,点I是△ABC的内心.
(1)求作过点I且平行于BC的直线,与AB,AC分别相交于点D,E(要求:尺规作图,不写作法,保留作图痕迹);
(2)若AB=6,AC=8,DE=,求BC的长.
【解答】解:(1)如图,连接BI,作∠DIB=∠IBC,直线ID交AC于E点,
则直线DE为所作;
(2)连接CI,如图,
∵点I是△ABC的内心,
∴BI平分∠ABC,CI平分∠ACB,
∴∠DBI=∠CBI,∠ECI=∠BCI,
∵DE∥BC,
∴∠DIB=∠CBI,∠EIC=∠BCI,
∴∠DIB=∠DBI,∠EIC=∠ECI,
∴DB=DI,EI=EC,
设BD=x,则DI=x,CE=EI=﹣﹣x,
∵DE∥BC,
∴BD:BA=CE:CA,
即x:6=(﹣x):8,
解得x=2,
∴AD=AB﹣BD=4,
∵DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=AD:AB,即:BC=4:6,
解得BC=7,
即BC的长为7.
24.(12分)已知:如图,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针旋转一个角度α得到Rt△ADE,连接BD,CE.
(1)如图①,当0°<α<45°时,求证:△ABD∽△ACE;
(2)如图②,当α=45°时,点E在AB的延长线上,延长DB交CE于点F,求∠DFE的度数;
(3)如图③,当45°<α<90°时,延长DB交CE于点F,求证:点F是线段CE的中点.
【解答】(1)证明:∵将△ABC绕点A逆时针旋一个角度α得到Rt△ADE,
∴AD=AB,AE=AC,∠BAD=∠CAE,
∴,
∴△ABD∽△ACE;
(2)解:如图,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠BAC=∠BCA=45°,
由旋转的性质可知:AD=AB,AE=AC,∠DAE=∠BAC=45°,
∴∠1=∠2=67.5°,∠3=∠ACE=67.5°,
∴∠2=∠4=67.5°,
∴∠BFE=180°﹣∠3﹣∠4=45°;
(3)证明:如图,过点E作EM⊥DF于点M,过点C作CN⊥DF,交DF的延长线于点N,
∴∠DME=∠EMF=∠BNC=90°,
由旋转的性质可知:DE=BC,AD=AB,∠ADE=∠ABC=90°,
∴∠1=∠2,∠1+∠4=90°,∠2+∠3=180°﹣∠ABC=90°,
∴∠3=∠4,
∴△DEM≌△BCN(AAS),
∴EM=CN,
又∵∠5=∠6,∠EMF=∠CNF=90°,
∴△FEM≌△FCN(AAS),
∴EF=CF,
即F是CE的中点.
25.(14分)如图,在平面直角坐标系中,抛物线y=x2+bx+c交x轴于A(﹣1,0),B(3,0)两点,交y轴于点C.
(1)求二次函数解析式;
(2)如图1,若在x轴上方的抛物线上存在一点D,使得∠ACD=45°,求点D的坐标;
(3)如图2,平面上一点E(3,2),过点E作任意一条直线交抛物线于P、Q两点,连接AP、AQ,分别交y轴于M、N两点,则OM与ON的积是否为定值?若是,求出此定值;若不是,请说明理由.
【解答】解:(1)设y=a(x﹣x1)(x﹣x2),
则y=(x﹣3)(x+1)=x2﹣2x﹣3;
(2)抛物线的表达式为y=x2﹣2x﹣3,则点C(0,﹣3),
过A作AK⊥AC交CD于点K,作KH⊥x轴于点H,如图1,
∵∠ACD=45°,
∴△CAK是等腰直角三角形,
∴AC=AK,
∵∠AOC=∠KHA=90°,∠ACO=90°﹣∠OAC=∠KAH,
∴△OAC≌△HKA(AAS),
∴AH=CO=3,KH=OA=1,
∴K(2,1),
设直线CD的解析式为y=kx﹣3,
∴2k﹣3=1,
∴k=2,
∴直线CD的解析式为y=2x﹣3,
联立,
解得x=0(舍去),或x=4,
∴D(4,5);
(3)OM与ON的积是定值,理由如下:
∵过点E(3,2)作一直线交抛物线于P、Q两点,
设直线PQ的解析式为y=ax+b,P(x1,y1),Q(x2,y2),
∴2=3a+b,b=2﹣3a,
∴直线PQ的解析式为y=ax+2﹣3a②,
联立①②得:x2+(1﹣3﹣a)x+3a﹣5=0,
∴x1+x2=a+2,x1 x2=3a﹣5,
如图2,作PS⊥x轴于点S,作QT⊥x轴于点T,
则△AMO∽△APS,
∴=,
即=,
∴OM=x1﹣3,
同理,ON=﹣(x2﹣3),
∴OM ON=﹣(x1﹣3)(x2﹣3)=﹣[x1 x2﹣3(x1+x2)+9]=﹣[3a﹣5﹣3(a+2)+9]=2,为定值.
第1页(共1页)
同课章节目录
