第三单元:圆柱与圆锥单元复习课件(共37张PPT)人教版六年级数学下册
文档属性
| 名称 | 第三单元:圆柱与圆锥单元复习课件(共37张PPT)人教版六年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 14:14:50 | ||
图片预览






文档简介
(共37张PPT)
圆柱与圆锥复习专题
人教版六年级数学下册
1
圆柱
2
圆锥
圆柱与圆锥
圆柱
圆柱的认识
圆柱的表面积
圆柱的体积
圆锥
圆锥的认识
圆锥的体积
1
圆柱
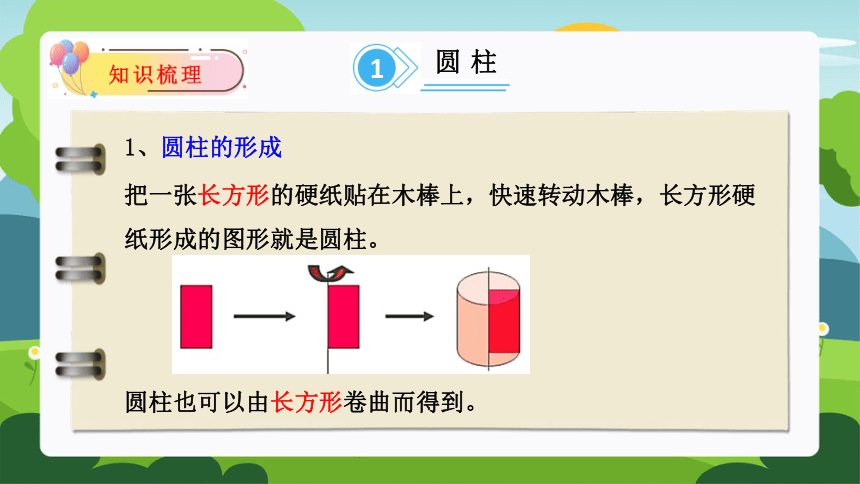
1、圆柱的形成
把一张长方形的硬纸贴在木棒上,快速转动木棒,长方形硬纸形成的图形就是圆柱。
圆柱也可以由长方形卷曲而得到。
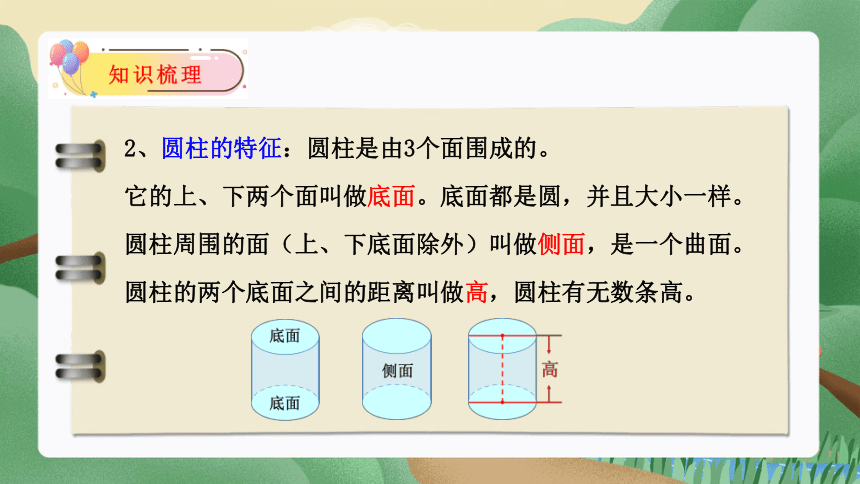
2、圆柱的特征:圆柱是由3个面围成的。
它的上、下两个面叫做底面。底面都是圆,并且大小一样。
圆柱周围的面(上、下底面除外)叫做侧面,是一个曲面。
圆柱的两个底面之间的距离叫做高,圆柱有无数条高。
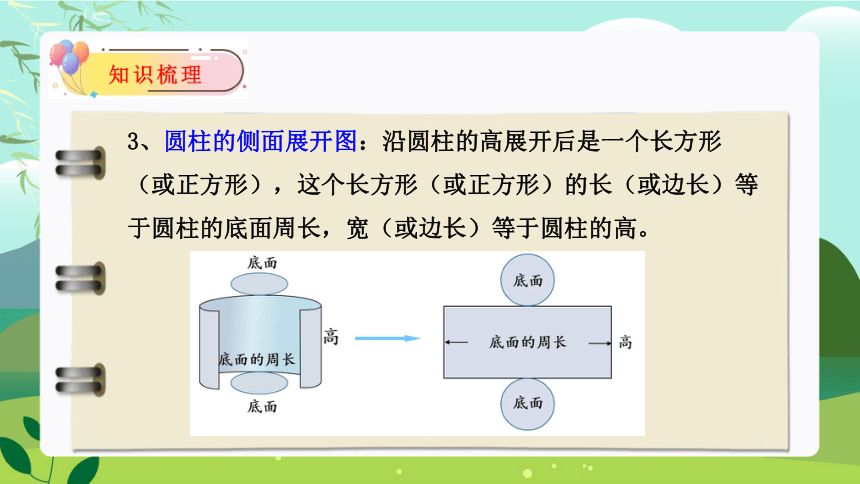
3、圆柱的侧面展开图:沿圆柱的高展开后是一个长方形(或正方形),这个长方形(或正方形)的长(或边长)等于圆柱的底面周长,宽(或边长)等于圆柱的高。
圆柱的认识
【例1】辩一辩,对的打√,错的打×。
(1)圆柱的侧面展开图不可能是平行四边形。( )
(1)如果不是沿着圆柱的高线剪开,而是斜着剪开,得到的侧面展开图就是平行四边形。所以是错误的。
×
圆柱的侧面展开图不可能是梯形。
【例1】辩一辩,对的打√,错的打×。
(2)如果圆柱的底面圆的周长和高都等于8cm,则这个圆柱的侧面展开图是一个正方形。( )
(2)如果圆柱的底面圆的周长和高都等于8cm,则这个圆柱的侧面展开图的长和宽相等,是一个正方形。
√
【例1】辩一辩,对的打√,错的打×。
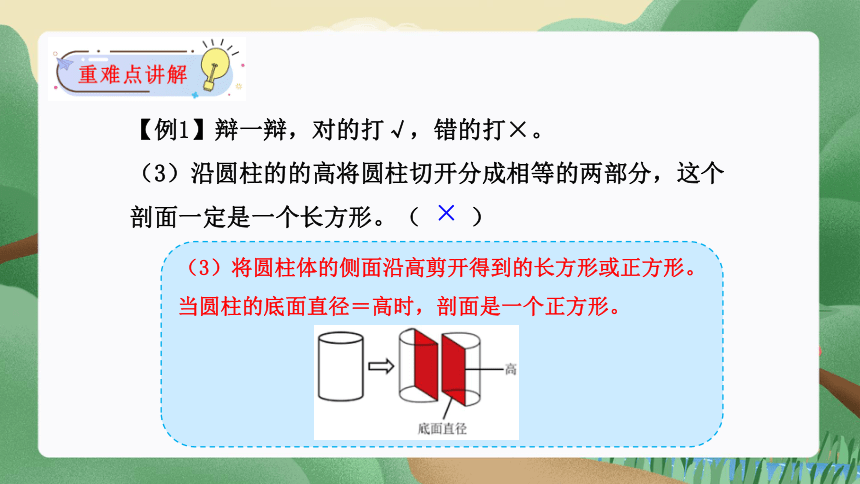
(3)沿圆柱的的高将圆柱切开分成相等的两部分,这个剖面一定是一个长方形。( )
(3)将圆柱体的侧面沿高剪开得到的长方形或正方形。
当圆柱的底面直径=高时,剖面是一个正方形。
×
【例2】一个底面半径是5厘米,高是8厘米的圆柱的沿高剪开,得到是一个长方形,则这个长方形的长是( )厘米,宽是( )厘米。
将一个圆柱沿高剪开得到的长方形,其长为圆柱的底面周长,宽为圆柱的高。已知圆柱的底面半径是5厘米,可得圆柱底面周长为:2×3.14×5=31.4(厘米)。所以这个长方形的长是31.4厘米,宽是8厘米。
31.4
8
圆的周长公式:C=2πr
1、一个圆柱底面半径是2cm,侧面展开图是一个正方形,则它的高是( )厘米。
因为圆柱的侧面展开图是一个正方形,所以圆柱的高等于底面圆的周长,
2×3.14×2
=6.28×2
=12.56(厘米)
12.56
圆柱的表面积
1、圆柱的侧面积
圆柱的侧面积=底面圆的周长×高
S侧=Ch=2πrh=πdh
2、圆柱的表面积:指的是圆柱表面的总面积。
圆柱的表面积=圆柱的侧面积+底面圆的面积×2
S表=Ch+2πr2
【例3】一个圆柱形茶叶罐底面半径是6厘米,高是10厘米。沿着这个茶叶罐的高剪开它侧面贴着的商标纸,这张商标纸的面积是多少平方厘米?
圆柱的侧面积公式为:S=2πrh
2×3.14×6×10
=6.28×6×10
=376.8(平方厘米)
答:这张商标纸的面积是376.8平方厘米。
【例4】一个圆柱的高是8厘米,底面周长是25.12厘米,这个圆柱的表面积是( )平方厘米。
底面圆半径r=C÷(2π)
25.12÷(2×3.14)
=25.14÷6.28
=4(厘米)
圆柱表面积S表=Ch+2πr2
25.12×8+ 2×3.14×42
=200.96+100.48
=301.44(平方厘米)
301.44
【例5】一个高是5分米,底面圆的直径是2分米圆柱形的无盖水桶的表面积是( )平方分米。
水桶的表面积=圆柱的侧面积+下底面圆面积
3.14×2×5+3.14×(2÷2)2
=31.4+3.14
=34.54(平方分米)
在实际应用中,并不是所有的圆柱形物体都有两个底面的,一定要具体问题具体分析。
34.54
【例6】有一个高是30分米、底面圆的直径是6分米圆柱形的烟囱,刘叔叔要用铁皮包这个烟囱,至少需要用多少平方分米的铁皮?(得数保留整数)
烟囱的表面积=圆柱的侧面积=πdh
3.14×6×30
=18.84×30
=565.2
≈566(平方分米)
答:至少需要用566平方分米的铁皮。
用“进一法”取近似数。
【例7】如果将一个圆柱的底面半径扩大3倍,高不变,则它的侧面积会扩大( )倍。
A、3 B、6 C、9
这个圆柱的底面半径为1厘米,则它的侧面积为2πrh。
如果将这个圆柱的底面半径扩大3倍,则新圆柱的半径为3r,
那么新圆柱的侧面积为:2π×(3r)×h=6πrh。
所以侧面积扩大了:(6πrh)÷(2πrh)=3。
A
圆柱的体积
1、圆柱所占空间的大小,叫做这个圆柱的体积。
2、圆柱的体积公式:
圆柱的体积=底面积×高
V圆柱=Sh
V圆柱=πr2h
【例8】有一段圆柱形钢管,底面半径是2分米,长是15分米。如果每立方分米的重5千克,这段钢管重多少千克?
V圆柱=πr2h
3.14×22×15
=3.14×4×15
=12.56×15
=188.4(平方分米)
钢管重量=圆柱体积×每立方米的重量
188.4×5=942(千克)
答:这段钢管重942千克。
【例9】将一瓶2升的牛奶倒入几个高是20厘米,底面半径是3厘米的圆柱形玻璃杯中,准备3个玻璃杯够装吗?
V圆柱=πr2h
1个玻璃杯的容积:
3.14×32×20
=3.14×9×20
=28.26×20
=565.2(立方厘米)
3个玻璃杯的总容积:
565.2×3=1695.6(立方厘米)
2升=2000立方厘米
2000>1695.6
答:准备3个玻璃杯不够装。
1升=1000立方厘米
【例10】往一个底面内直径是20厘米的圆柱形水桶中装水,再将一个铁块放入在这个水桶中,已知将铁块取出后,水面下降了5厘米。这个铁块的体积是多少平方厘米?
底面半径=直径÷2
20÷2=10(厘米)
V圆柱=πr2h
下降的水的体积为:
3.14×102×5
=314×5
=1570(立方厘米)
答:这个铁块的体积是1570平方厘米。
根据排水法可知,铁块的体积等于它排开的水的体积,所以只需要求出下降的水的体积,即可得到铁块的体积。
瓶子的容积除以(16+4)厘米就是瓶子的底面积。
用瓶子的底面积乘正放时瓶子里饮料的高,就是瓶内饮料的体积。
【例11】如下图,一个容积是500mL的可乐瓶的瓶身是圆柱形,瓶里装有可乐。将可乐瓶正放时,可乐高16cm;盖紧瓶盖倒放时,空余部分高4cm。瓶中可乐的体积是多少mL?
不论正放还是倒放,瓶子的容积、可乐的体积、无可乐部分的空瓶体积都不会改变。
500mL=500cm3
500÷(16+4)×16
=25×16
=400(cm3)
=400mL
【例11】如下图,一个容积是500mL的可乐瓶的瓶身是圆柱形,瓶里装有可乐。将可乐瓶正放时,可乐高16cm;盖紧瓶盖倒放时,空余部分高4cm。瓶中可乐的体积是多少mL?
可以利用体积不变的特性,把不规则图形转化成规则图形来计算体积。
答:可乐的体积是400mL。
2
圆锥
1、圆锥的形成:
把一张直角三角形的硬纸贴在木棒上,快速转动木棒,直角三角形转动形成的图形是圆锥。贴在木棒上的直角边是圆锥的高,另一条直角边是圆锥的底面半径。
圆锥也可以由扇形卷曲而得到。
2、圆锥的特征:
(1)底面:圆锥的底面是一个圆。
(2)侧面:圆锥的侧面是一个曲面。
(3)高:圆锥的高是圆锥的顶点到底面圆心的距离。圆锥只有一条高。
圆锥的认识
【例12】辩一辩,对的打√,错的打×。
(1)沿着圆锥的高垂直于底面将圆锥切开,得到的截面是一个等腰三角形。( )
(1)当沿着圆锥的高垂直于底面将其切开时,所得到的截面是一个等腰三角形。
√
【例12】辩一辩,对的打√,错的打×。
(2)以直角三角形的一条边为轴旋转一周,可以得到一个圆锥。( )
(2)如果这条边是直角边,那么可以得到一个圆锥;
如果这条边是斜边,则会得到一个由两个圆锥组成的物体,而不是一个单独的圆锥。
×
【例12】辩一辩,对的打√,错的打×。
(3)在圆锥上任意切一刀,得到的截面可能是长方形。( )
(3)在圆锥上任意切一刀,截面可能是三角形、圆、椭圆等图形,但是不可能是长方形。
×
1、将下面的平面图形绕着轴旋转一周,得到的立体图形是( )。
A、 B、 C、
A
圆锥的体积
圆锥的计算公式:
底面积:S底=πr
底面周长:C底=πd=2πr
体积:V锥= S底h= πr h
【例13】将一个高为10厘米的圆锥,沿圆锥的高切开,分成大小、形状完全相同的两个部分,这个圆锥的表面积增加60平方厘米。则这个圆锥体的体积是多少立方厘米?
由题意可知:增加的面积即是两个以圆锥的底面直径为底,圆锥的高为高的三角形的面积之和。
【例13】将一个高为10厘米的圆锥,沿圆锥的高切开,分成大小、形状完全相同的两个部分,这个圆锥的表面积增加60平方厘米。则这个圆锥体的体积是多少立方厘米?
三角形面积=增加的面积÷2
60÷2=30(平方厘米)
底面直径=三角形面积×2÷高
30×2÷10
=60÷10
=6(厘米)
底面半径=底面直径÷2
6÷2=3(厘米)
V锥= πr h
×3.14×3 ×10
=9.42×10
=94.2(立方厘米)
【例14】将一个圆锥的高扩大到原来的2倍,底面半径缩小到原来的,则圆锥的体积( )。
A、缩小到原来的 C.扩大到原来的2倍 B.不变
假设原来圆锥的底面半径为r,高为h,则原来圆锥体积为:
V原来= πr h;
现在圆锥的底面半径为r,高为2h,则现在圆锥体积为:
V现在= π×(r) ×2h = πr h;
所以V现在÷ V原来= πr h ÷ πr h = 。
A
1、一个圆柱的侧面展开图是一个长方形,这个长方形的长等于圆柱的( ),宽等于圆柱的( )。
2、一个圆柱的高是7厘米,底面周长是15.7厘米,如果沿着这个圆柱的底面直径把它切割成两个半圆柱,圆柱增加的面积共是( )平方厘米。
底面周长
高
70
3、有一根圆柱形的木桩,底面积是2.8平方米,长是1.6米,这个圆柱形木桩的体积是( )立方米。
A、8.96 B、4.48 C、2.24
4、一个圆柱的体积是2.7立方分米,则与这个圆柱等底等高的圆锥的体积是( )立方分米。
A、8.1 B、2.7 C、0.9
B
C
5、下面图形哪些是圆柱?在对应的( )里画“△”。哪些是圆锥?在对应的( )里画“□”。
( ) ( ) ( ) ( ) ( ) ( )
□
□
△
每一份努力,都将在学习中得到最好的回报。加油!
圆柱与圆锥复习专题
人教版六年级数学下册
1
圆柱
2
圆锥
圆柱与圆锥
圆柱
圆柱的认识
圆柱的表面积
圆柱的体积
圆锥
圆锥的认识
圆锥的体积
1
圆柱
1、圆柱的形成
把一张长方形的硬纸贴在木棒上,快速转动木棒,长方形硬纸形成的图形就是圆柱。
圆柱也可以由长方形卷曲而得到。
2、圆柱的特征:圆柱是由3个面围成的。
它的上、下两个面叫做底面。底面都是圆,并且大小一样。
圆柱周围的面(上、下底面除外)叫做侧面,是一个曲面。
圆柱的两个底面之间的距离叫做高,圆柱有无数条高。
3、圆柱的侧面展开图:沿圆柱的高展开后是一个长方形(或正方形),这个长方形(或正方形)的长(或边长)等于圆柱的底面周长,宽(或边长)等于圆柱的高。
圆柱的认识
【例1】辩一辩,对的打√,错的打×。
(1)圆柱的侧面展开图不可能是平行四边形。( )
(1)如果不是沿着圆柱的高线剪开,而是斜着剪开,得到的侧面展开图就是平行四边形。所以是错误的。
×
圆柱的侧面展开图不可能是梯形。
【例1】辩一辩,对的打√,错的打×。
(2)如果圆柱的底面圆的周长和高都等于8cm,则这个圆柱的侧面展开图是一个正方形。( )
(2)如果圆柱的底面圆的周长和高都等于8cm,则这个圆柱的侧面展开图的长和宽相等,是一个正方形。
√
【例1】辩一辩,对的打√,错的打×。
(3)沿圆柱的的高将圆柱切开分成相等的两部分,这个剖面一定是一个长方形。( )
(3)将圆柱体的侧面沿高剪开得到的长方形或正方形。
当圆柱的底面直径=高时,剖面是一个正方形。
×
【例2】一个底面半径是5厘米,高是8厘米的圆柱的沿高剪开,得到是一个长方形,则这个长方形的长是( )厘米,宽是( )厘米。
将一个圆柱沿高剪开得到的长方形,其长为圆柱的底面周长,宽为圆柱的高。已知圆柱的底面半径是5厘米,可得圆柱底面周长为:2×3.14×5=31.4(厘米)。所以这个长方形的长是31.4厘米,宽是8厘米。
31.4
8
圆的周长公式:C=2πr
1、一个圆柱底面半径是2cm,侧面展开图是一个正方形,则它的高是( )厘米。
因为圆柱的侧面展开图是一个正方形,所以圆柱的高等于底面圆的周长,
2×3.14×2
=6.28×2
=12.56(厘米)
12.56
圆柱的表面积
1、圆柱的侧面积
圆柱的侧面积=底面圆的周长×高
S侧=Ch=2πrh=πdh
2、圆柱的表面积:指的是圆柱表面的总面积。
圆柱的表面积=圆柱的侧面积+底面圆的面积×2
S表=Ch+2πr2
【例3】一个圆柱形茶叶罐底面半径是6厘米,高是10厘米。沿着这个茶叶罐的高剪开它侧面贴着的商标纸,这张商标纸的面积是多少平方厘米?
圆柱的侧面积公式为:S=2πrh
2×3.14×6×10
=6.28×6×10
=376.8(平方厘米)
答:这张商标纸的面积是376.8平方厘米。
【例4】一个圆柱的高是8厘米,底面周长是25.12厘米,这个圆柱的表面积是( )平方厘米。
底面圆半径r=C÷(2π)
25.12÷(2×3.14)
=25.14÷6.28
=4(厘米)
圆柱表面积S表=Ch+2πr2
25.12×8+ 2×3.14×42
=200.96+100.48
=301.44(平方厘米)
301.44
【例5】一个高是5分米,底面圆的直径是2分米圆柱形的无盖水桶的表面积是( )平方分米。
水桶的表面积=圆柱的侧面积+下底面圆面积
3.14×2×5+3.14×(2÷2)2
=31.4+3.14
=34.54(平方分米)
在实际应用中,并不是所有的圆柱形物体都有两个底面的,一定要具体问题具体分析。
34.54
【例6】有一个高是30分米、底面圆的直径是6分米圆柱形的烟囱,刘叔叔要用铁皮包这个烟囱,至少需要用多少平方分米的铁皮?(得数保留整数)
烟囱的表面积=圆柱的侧面积=πdh
3.14×6×30
=18.84×30
=565.2
≈566(平方分米)
答:至少需要用566平方分米的铁皮。
用“进一法”取近似数。
【例7】如果将一个圆柱的底面半径扩大3倍,高不变,则它的侧面积会扩大( )倍。
A、3 B、6 C、9
这个圆柱的底面半径为1厘米,则它的侧面积为2πrh。
如果将这个圆柱的底面半径扩大3倍,则新圆柱的半径为3r,
那么新圆柱的侧面积为:2π×(3r)×h=6πrh。
所以侧面积扩大了:(6πrh)÷(2πrh)=3。
A
圆柱的体积
1、圆柱所占空间的大小,叫做这个圆柱的体积。
2、圆柱的体积公式:
圆柱的体积=底面积×高
V圆柱=Sh
V圆柱=πr2h
【例8】有一段圆柱形钢管,底面半径是2分米,长是15分米。如果每立方分米的重5千克,这段钢管重多少千克?
V圆柱=πr2h
3.14×22×15
=3.14×4×15
=12.56×15
=188.4(平方分米)
钢管重量=圆柱体积×每立方米的重量
188.4×5=942(千克)
答:这段钢管重942千克。
【例9】将一瓶2升的牛奶倒入几个高是20厘米,底面半径是3厘米的圆柱形玻璃杯中,准备3个玻璃杯够装吗?
V圆柱=πr2h
1个玻璃杯的容积:
3.14×32×20
=3.14×9×20
=28.26×20
=565.2(立方厘米)
3个玻璃杯的总容积:
565.2×3=1695.6(立方厘米)
2升=2000立方厘米
2000>1695.6
答:准备3个玻璃杯不够装。
1升=1000立方厘米
【例10】往一个底面内直径是20厘米的圆柱形水桶中装水,再将一个铁块放入在这个水桶中,已知将铁块取出后,水面下降了5厘米。这个铁块的体积是多少平方厘米?
底面半径=直径÷2
20÷2=10(厘米)
V圆柱=πr2h
下降的水的体积为:
3.14×102×5
=314×5
=1570(立方厘米)
答:这个铁块的体积是1570平方厘米。
根据排水法可知,铁块的体积等于它排开的水的体积,所以只需要求出下降的水的体积,即可得到铁块的体积。
瓶子的容积除以(16+4)厘米就是瓶子的底面积。
用瓶子的底面积乘正放时瓶子里饮料的高,就是瓶内饮料的体积。
【例11】如下图,一个容积是500mL的可乐瓶的瓶身是圆柱形,瓶里装有可乐。将可乐瓶正放时,可乐高16cm;盖紧瓶盖倒放时,空余部分高4cm。瓶中可乐的体积是多少mL?
不论正放还是倒放,瓶子的容积、可乐的体积、无可乐部分的空瓶体积都不会改变。
500mL=500cm3
500÷(16+4)×16
=25×16
=400(cm3)
=400mL
【例11】如下图,一个容积是500mL的可乐瓶的瓶身是圆柱形,瓶里装有可乐。将可乐瓶正放时,可乐高16cm;盖紧瓶盖倒放时,空余部分高4cm。瓶中可乐的体积是多少mL?
可以利用体积不变的特性,把不规则图形转化成规则图形来计算体积。
答:可乐的体积是400mL。
2
圆锥
1、圆锥的形成:
把一张直角三角形的硬纸贴在木棒上,快速转动木棒,直角三角形转动形成的图形是圆锥。贴在木棒上的直角边是圆锥的高,另一条直角边是圆锥的底面半径。
圆锥也可以由扇形卷曲而得到。
2、圆锥的特征:
(1)底面:圆锥的底面是一个圆。
(2)侧面:圆锥的侧面是一个曲面。
(3)高:圆锥的高是圆锥的顶点到底面圆心的距离。圆锥只有一条高。
圆锥的认识
【例12】辩一辩,对的打√,错的打×。
(1)沿着圆锥的高垂直于底面将圆锥切开,得到的截面是一个等腰三角形。( )
(1)当沿着圆锥的高垂直于底面将其切开时,所得到的截面是一个等腰三角形。
√
【例12】辩一辩,对的打√,错的打×。
(2)以直角三角形的一条边为轴旋转一周,可以得到一个圆锥。( )
(2)如果这条边是直角边,那么可以得到一个圆锥;
如果这条边是斜边,则会得到一个由两个圆锥组成的物体,而不是一个单独的圆锥。
×
【例12】辩一辩,对的打√,错的打×。
(3)在圆锥上任意切一刀,得到的截面可能是长方形。( )
(3)在圆锥上任意切一刀,截面可能是三角形、圆、椭圆等图形,但是不可能是长方形。
×
1、将下面的平面图形绕着轴旋转一周,得到的立体图形是( )。
A、 B、 C、
A
圆锥的体积
圆锥的计算公式:
底面积:S底=πr
底面周长:C底=πd=2πr
体积:V锥= S底h= πr h
【例13】将一个高为10厘米的圆锥,沿圆锥的高切开,分成大小、形状完全相同的两个部分,这个圆锥的表面积增加60平方厘米。则这个圆锥体的体积是多少立方厘米?
由题意可知:增加的面积即是两个以圆锥的底面直径为底,圆锥的高为高的三角形的面积之和。
【例13】将一个高为10厘米的圆锥,沿圆锥的高切开,分成大小、形状完全相同的两个部分,这个圆锥的表面积增加60平方厘米。则这个圆锥体的体积是多少立方厘米?
三角形面积=增加的面积÷2
60÷2=30(平方厘米)
底面直径=三角形面积×2÷高
30×2÷10
=60÷10
=6(厘米)
底面半径=底面直径÷2
6÷2=3(厘米)
V锥= πr h
×3.14×3 ×10
=9.42×10
=94.2(立方厘米)
【例14】将一个圆锥的高扩大到原来的2倍,底面半径缩小到原来的,则圆锥的体积( )。
A、缩小到原来的 C.扩大到原来的2倍 B.不变
假设原来圆锥的底面半径为r,高为h,则原来圆锥体积为:
V原来= πr h;
现在圆锥的底面半径为r,高为2h,则现在圆锥体积为:
V现在= π×(r) ×2h = πr h;
所以V现在÷ V原来= πr h ÷ πr h = 。
A
1、一个圆柱的侧面展开图是一个长方形,这个长方形的长等于圆柱的( ),宽等于圆柱的( )。
2、一个圆柱的高是7厘米,底面周长是15.7厘米,如果沿着这个圆柱的底面直径把它切割成两个半圆柱,圆柱增加的面积共是( )平方厘米。
底面周长
高
70
3、有一根圆柱形的木桩,底面积是2.8平方米,长是1.6米,这个圆柱形木桩的体积是( )立方米。
A、8.96 B、4.48 C、2.24
4、一个圆柱的体积是2.7立方分米,则与这个圆柱等底等高的圆锥的体积是( )立方分米。
A、8.1 B、2.7 C、0.9
B
C
5、下面图形哪些是圆柱?在对应的( )里画“△”。哪些是圆锥?在对应的( )里画“□”。
( ) ( ) ( ) ( ) ( ) ( )
□
□
△
每一份努力,都将在学习中得到最好的回报。加油!
