第五章 相交线与平行线 单元测试卷(含答案) 2023—2024学年人教版数学七年级下册
文档属性
| 名称 | 第五章 相交线与平行线 单元测试卷(含答案) 2023—2024学年人教版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 467.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 07:09:04 | ||
图片预览

文档简介
第五单元测试卷
一、选择题(共14题.1~10题每题3分,11~14题每题2分,共38分)
1.如图,在所标识的角中,互为对顶角的两个角是 ( )
A.∠2和∠3 B.∠1和∠3 C.∠1和∠4 D.∠1和∠2
2.如图所示,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成 ( )
A.内错角 B.同位角 C.同旁内角 D.对顶角
3.体育课上,老师测量小明跳远成绩的依据是 ( )
A.过直线上一点且垂直于这条直线的直线有且只有一条
B.两点之间,线段最短
C.垂线段最短
D.两点确定一条直线
4.下列图形中,线段AD的长表示点A到直线BC距离的是 ( )
A B C D
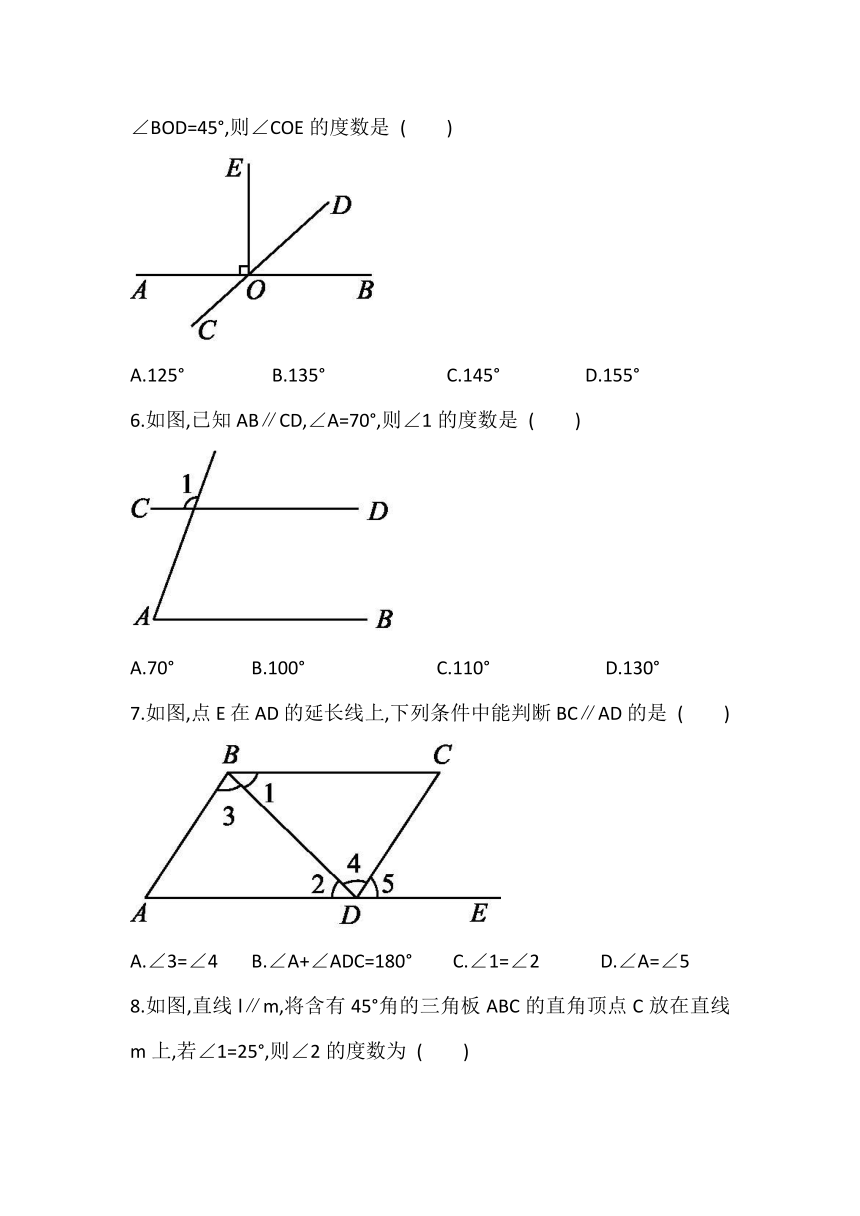
5.如图,直线AB与直线CD相交于点O,E是∠AOD内一点,已知OE⊥AB,
∠BOD=45°,则∠COE的度数是 ( )
A.125° B.135° C.145° D.155°
6.如图,已知AB∥CD,∠A=70°,则∠1的度数是 ( )
A.70° B.100° C.110° D.130°
7.如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是 ( )
A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5
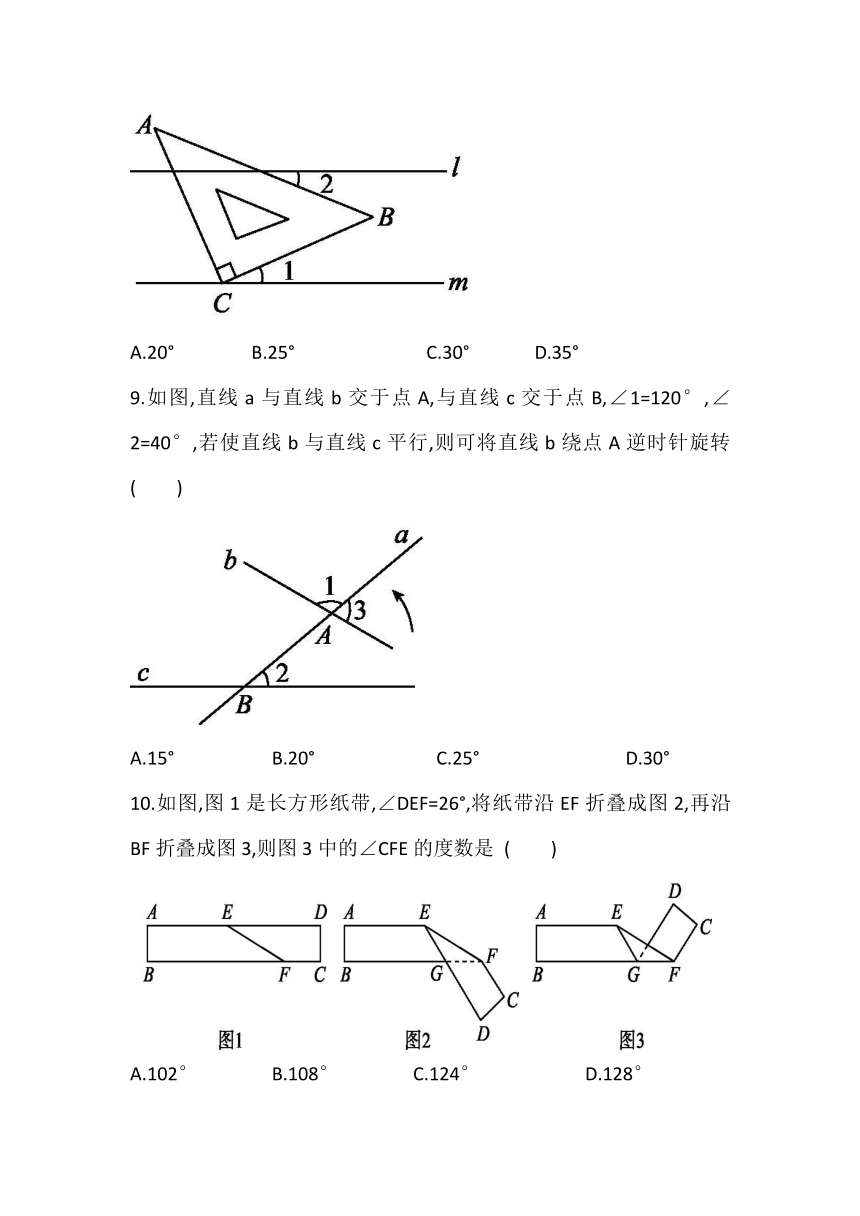
8.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为 ( )
A.20° B.25° C.30° D.35°
9.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A.15° B.20° C.25° D.30°
10.如图,图1是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数是 ( )
A.102° B.108° C.124° D.128°
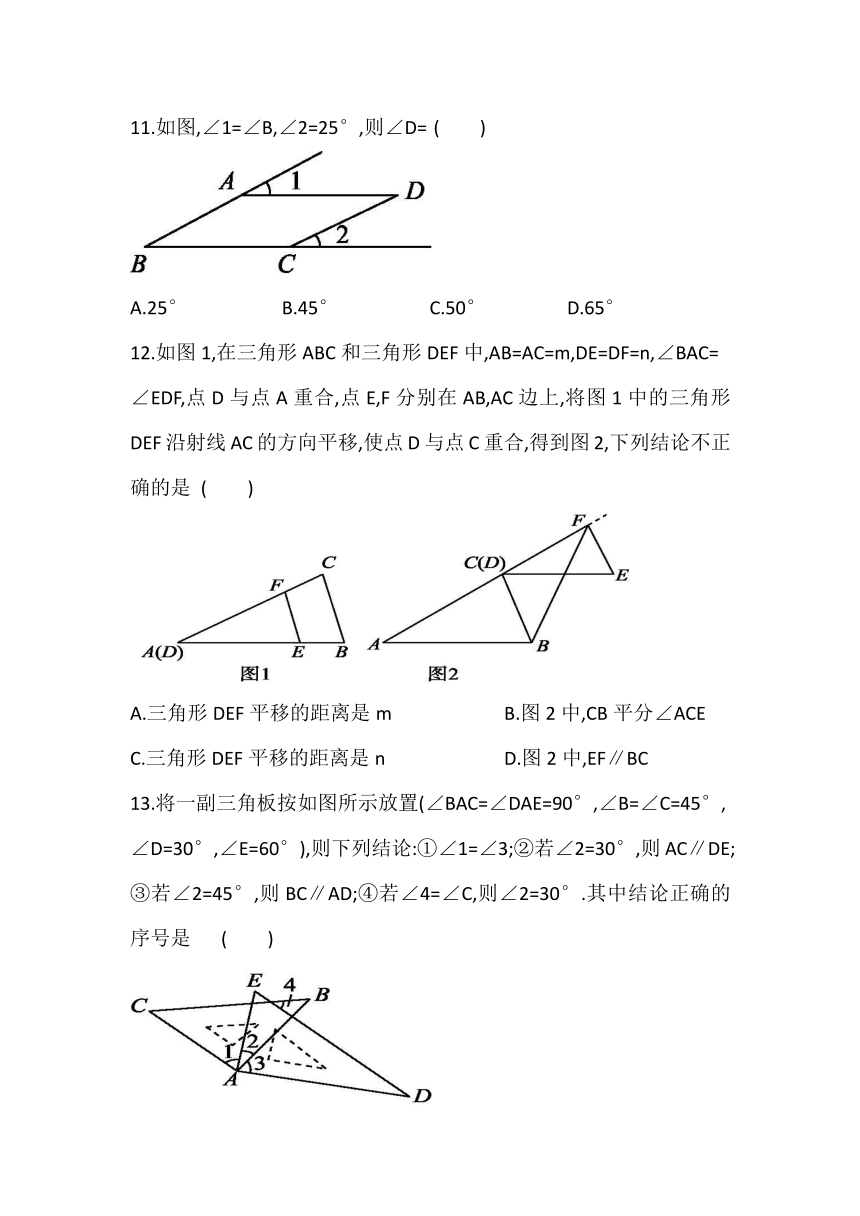
11.如图,∠1=∠B,∠2=25°,则∠D= ( )
A.25° B.45° C.50° D.65°
12.如图1,在三角形ABC和三角形DEF中,AB=AC=m,DE=DF=n,∠BAC=
∠EDF,点D与点A重合,点E,F分别在AB,AC边上,将图1中的三角形DEF沿射线AC的方向平移,使点D与点C重合,得到图2,下列结论不正确的是 ( )
A.三角形DEF平移的距离是m B.图2中,CB平分∠ACE
C.三角形DEF平移的距离是n D.图2中,EF∥BC
13.将一副三角板按如图所示放置(∠BAC=∠DAE=90°,∠B=∠C=45°,
∠D=30°,∠E=60°),则下列结论:①∠1=∠3;②若∠2=30°,则AC∥DE;③若∠2=45°,则BC∥AD;④若∠4=∠C,则∠2=30°.其中结论正确的序号是 ( )
A.①②③ B.①②④
C.③④ D.①②③④
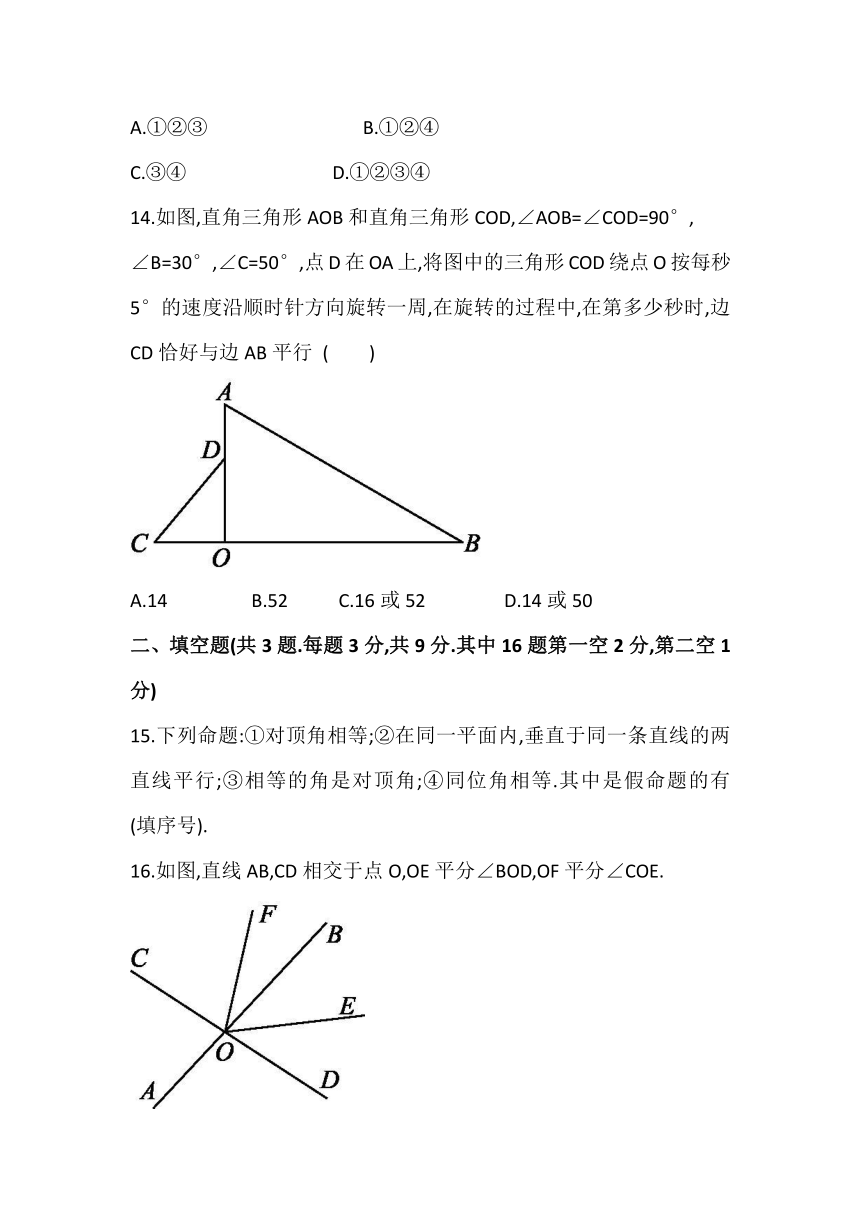
14.如图,直角三角形AOB和直角三角形COD,∠AOB=∠COD=90°,
∠B=30°,∠C=50°,点D在OA上,将图中的三角形COD绕点O按每秒5°的速度沿顺时针方向旋转一周,在旋转的过程中,在第多少秒时,边CD恰好与边AB平行 ( )
A.14 B.52 C.16或52 D.14或50
二、填空题(共3题.每题3分,共9分.其中16题第一空2分,第二空1分)
15.下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中是假命题的有 (填序号).
16.如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,∠BOF=___________°;
(2)若∠BOF=36°,∠AOC=___________°.
17.如图,在直角三角形ABC的斜边AB上有五个小直角三角形,已知大直角三角形的周长为60 cm,则这五个小直角三角形的周长的和为_______.
三、解答题(共53分)
18.(6分)(1)画图:先把三角形向左平移3个单位长度,再向下平移1个单位长度;
(2)写出平移后三角形的面积是_______.
19.(8分)如图,∠1+∠2=180°,证明AB∥CD.
证明:∵∠2+∠3=180°( ),
∠1+∠2=180°( ),
∴∠3=∠1( ).
∴AB∥CD( ).
20.(8分)如图,∠1=105°,∠2=105°,∠3=95°,求∠4的度数.
21.(9分)如图,∠BAD+∠ADH=180°,DF平分∠CDA,AE平分∠BAD,那么AE∥DF吗 说明理由.
22.(10分)如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.
求证:CD⊥AB.
23.(12分)如图,AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与点B,D重合).∠ABC=n°,∠ADC=80°.
(1)若点B在点A的左侧,求∠BED的度数(用含n的代数式表示).
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠BED的度数是否改变.若改变,请求出∠BED的度数(用含n的代数式表示);若不变,请说明理由.
参考答案
1、A
2、A
3、C
4、D
5、B
6、C
7.C
8、A
9.B
10.A
11.A
12.C
13.D
14.C
15.③④
16.(1)33 (2)72
17.60 cm
18.(1)
(2)3.5
19.
20.
解:∵∠1=105°,∠2=105°,∴∠1=∠2.
∴l1∥l2.∴∠4+∠3=180°.
∵∠3=95°,∴∠4=85°.
21
解:AE∥DF.
理由:∵∠BAD+∠ADH=180°,
∴AB∥CH(同旁内角互补,两直线平行).
∴∠CDA=∠DAB.
又∵AE平分∠DAB,DF平分∠CDA,∴∠1=∠2.
∴AE∥DF(内错角相等,两直线平行).
22.
证明:∵DG⊥BC,AC⊥BC(已知),
∴∠DGC=90°,∠ACB=90°(垂直定义).
∴∠DGC+∠ACB=180°.
∴DG∥AC(同旁内角互补,两直线平行).
∴∠2=∠DCA(两直线平行,内错角相等).
∵∠1=∠2(已知),∴∠1=∠DCA(等量代换).
∴EF∥CD(同位角相等,两直线平行).
∴∠AEF=∠ADC(两直线平行,同位角相等).
∵EF⊥AB(已知),∴∠AEF=90°(垂直定义).
∴∠ADC=90°(等量代换).∴CD⊥AB(垂直定义).
23(1)
(2)
一、选择题(共14题.1~10题每题3分,11~14题每题2分,共38分)
1.如图,在所标识的角中,互为对顶角的两个角是 ( )
A.∠2和∠3 B.∠1和∠3 C.∠1和∠4 D.∠1和∠2
2.如图所示,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成 ( )
A.内错角 B.同位角 C.同旁内角 D.对顶角
3.体育课上,老师测量小明跳远成绩的依据是 ( )
A.过直线上一点且垂直于这条直线的直线有且只有一条
B.两点之间,线段最短
C.垂线段最短
D.两点确定一条直线
4.下列图形中,线段AD的长表示点A到直线BC距离的是 ( )
A B C D
5.如图,直线AB与直线CD相交于点O,E是∠AOD内一点,已知OE⊥AB,
∠BOD=45°,则∠COE的度数是 ( )
A.125° B.135° C.145° D.155°
6.如图,已知AB∥CD,∠A=70°,则∠1的度数是 ( )
A.70° B.100° C.110° D.130°
7.如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是 ( )
A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5
8.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为 ( )
A.20° B.25° C.30° D.35°
9.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A.15° B.20° C.25° D.30°
10.如图,图1是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数是 ( )
A.102° B.108° C.124° D.128°
11.如图,∠1=∠B,∠2=25°,则∠D= ( )
A.25° B.45° C.50° D.65°
12.如图1,在三角形ABC和三角形DEF中,AB=AC=m,DE=DF=n,∠BAC=
∠EDF,点D与点A重合,点E,F分别在AB,AC边上,将图1中的三角形DEF沿射线AC的方向平移,使点D与点C重合,得到图2,下列结论不正确的是 ( )
A.三角形DEF平移的距离是m B.图2中,CB平分∠ACE
C.三角形DEF平移的距离是n D.图2中,EF∥BC
13.将一副三角板按如图所示放置(∠BAC=∠DAE=90°,∠B=∠C=45°,
∠D=30°,∠E=60°),则下列结论:①∠1=∠3;②若∠2=30°,则AC∥DE;③若∠2=45°,则BC∥AD;④若∠4=∠C,则∠2=30°.其中结论正确的序号是 ( )
A.①②③ B.①②④
C.③④ D.①②③④
14.如图,直角三角形AOB和直角三角形COD,∠AOB=∠COD=90°,
∠B=30°,∠C=50°,点D在OA上,将图中的三角形COD绕点O按每秒5°的速度沿顺时针方向旋转一周,在旋转的过程中,在第多少秒时,边CD恰好与边AB平行 ( )
A.14 B.52 C.16或52 D.14或50
二、填空题(共3题.每题3分,共9分.其中16题第一空2分,第二空1分)
15.下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中是假命题的有 (填序号).
16.如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,∠BOF=___________°;
(2)若∠BOF=36°,∠AOC=___________°.
17.如图,在直角三角形ABC的斜边AB上有五个小直角三角形,已知大直角三角形的周长为60 cm,则这五个小直角三角形的周长的和为_______.
三、解答题(共53分)
18.(6分)(1)画图:先把三角形向左平移3个单位长度,再向下平移1个单位长度;
(2)写出平移后三角形的面积是_______.
19.(8分)如图,∠1+∠2=180°,证明AB∥CD.
证明:∵∠2+∠3=180°( ),
∠1+∠2=180°( ),
∴∠3=∠1( ).
∴AB∥CD( ).
20.(8分)如图,∠1=105°,∠2=105°,∠3=95°,求∠4的度数.
21.(9分)如图,∠BAD+∠ADH=180°,DF平分∠CDA,AE平分∠BAD,那么AE∥DF吗 说明理由.
22.(10分)如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.
求证:CD⊥AB.
23.(12分)如图,AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与点B,D重合).∠ABC=n°,∠ADC=80°.
(1)若点B在点A的左侧,求∠BED的度数(用含n的代数式表示).
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠BED的度数是否改变.若改变,请求出∠BED的度数(用含n的代数式表示);若不变,请说明理由.
参考答案
1、A
2、A
3、C
4、D
5、B
6、C
7.C
8、A
9.B
10.A
11.A
12.C
13.D
14.C
15.③④
16.(1)33 (2)72
17.60 cm
18.(1)
(2)3.5
19.
20.
解:∵∠1=105°,∠2=105°,∴∠1=∠2.
∴l1∥l2.∴∠4+∠3=180°.
∵∠3=95°,∴∠4=85°.
21
解:AE∥DF.
理由:∵∠BAD+∠ADH=180°,
∴AB∥CH(同旁内角互补,两直线平行).
∴∠CDA=∠DAB.
又∵AE平分∠DAB,DF平分∠CDA,∴∠1=∠2.
∴AE∥DF(内错角相等,两直线平行).
22.
证明:∵DG⊥BC,AC⊥BC(已知),
∴∠DGC=90°,∠ACB=90°(垂直定义).
∴∠DGC+∠ACB=180°.
∴DG∥AC(同旁内角互补,两直线平行).
∴∠2=∠DCA(两直线平行,内错角相等).
∵∠1=∠2(已知),∴∠1=∠DCA(等量代换).
∴EF∥CD(同位角相等,两直线平行).
∴∠AEF=∠ADC(两直线平行,同位角相等).
∵EF⊥AB(已知),∴∠AEF=90°(垂直定义).
∴∠ADC=90°(等量代换).∴CD⊥AB(垂直定义).
23(1)
(2)
