八年级数学上册 6.6 一次函数、一元一次方程和一元一次不等式学案 苏科版
文档属性
| 名称 | 八年级数学上册 6.6 一次函数、一元一次方程和一元一次不等式学案 苏科版 |

|
|
| 格式 | zip | ||
| 文件大小 | 40.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-26 22:32:23 | ||
图片预览

文档简介
6.6一次函数、一元一次方程和一元一次不等式
班级 姓名
一 、学习目标
1、经历实际问题中数量关系的分析、抽象,得出一元一次不等式与一元一次方程、一次函数的内在联系
2、会利用不等式、方程、函数的内在联系解决问题
3.根据具体的问题情景,选用合适的工具进行解决问题;
4、通过解决实际问题,知道数学与人类生活的密切联系以及对人类历史发展的作用.并以此激发学习数学的信心和兴趣.
二 、学习重点:一元一次不等式与一元一次方程、一次函数的内在联系
三、学习难点:根据情景中所表达的关系,选用合适的工具解决问题
四、学习过程
一、情境引入:
一根长20cm的弹簧,一端固定,另一端挂物体。在弹簧伸长后的长度不超过30cm的限度内,每挂1㎏质量的物体,弹簧伸长0.5cm.如果所挂物体的质量为x㎏,弹簧的长度是ycm。 (1)求y与x之间的函数关系式,并画出函数的图象。(2)求弹簧所挂物体的最大质量是多少?
二、概括总结:
三、例1 :某人点燃一根长25cm的蜡烛,已知蜡烛每小时缩短5cm,设x h后蜡烛剩下的长度为y cm.
(1)求y与x之间的函数关系式.
(2)几小时后,蜡烛的长度不足10cm?
四、练习一:
1.x取什么值时,函数y=-2(x+1)+4的值 是正数?负数?非负数?大于6?
2. 声音在空气中的传播速度y (m/s)(简称音速)与气温x(℃)满足
关系式 .。求
(1)音速为340m/s时的气温(2)音速超过340m/s时的气温范围
五.例2 :兄弟俩赛跑,哥哥先让弟弟跑9 m,然后自己才开始跑,已知弟弟每秒跑3 m,哥哥每秒跑4 m,列出函数关系式,回答下列问题:
(1)何时弟弟跑在哥哥前面?(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20 m?谁先跑过100 m?
六. 练习二
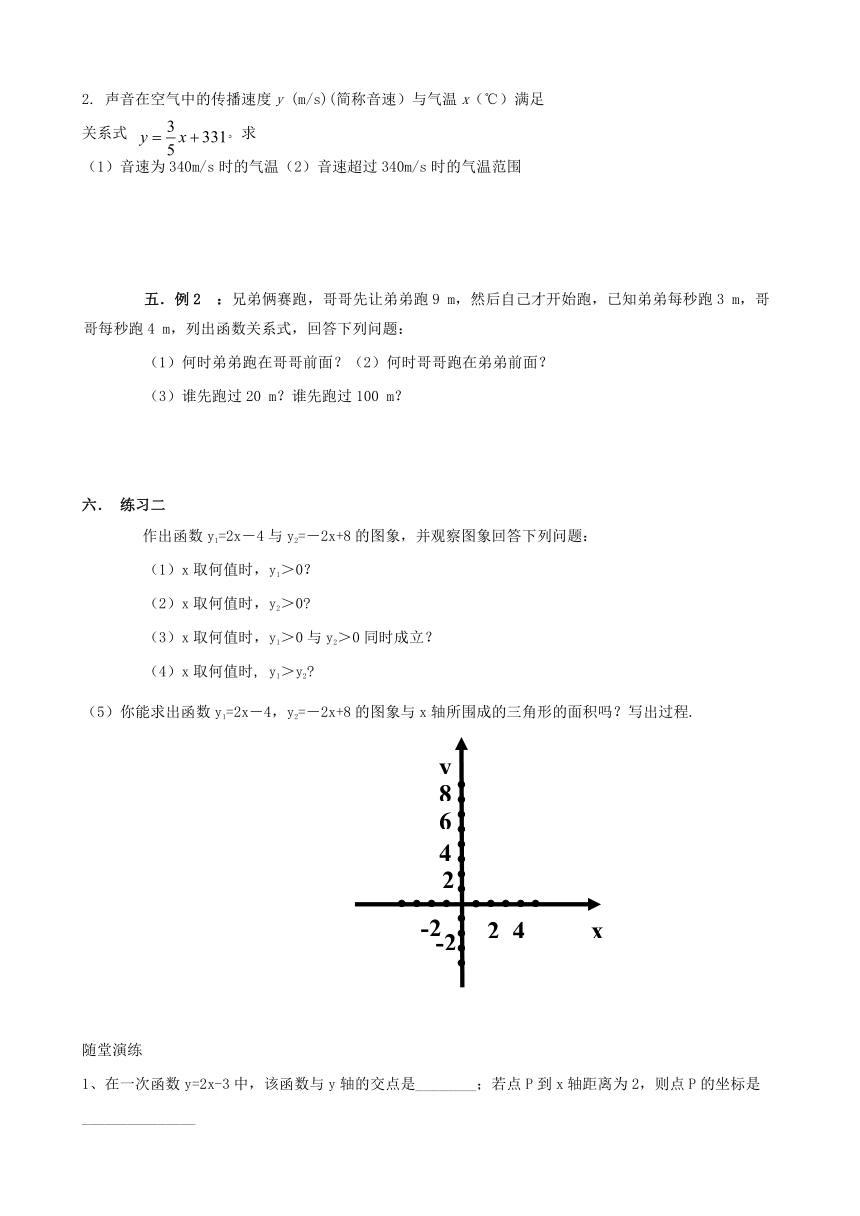
作出函数y1=2x-4与y2=-2x+8的图象,并观察图象回答下列问题:
(1)x取何值时,y1>0?
(2)x取何值时,y2>0
(3)x取何值时,y1>0与y2>0同时成立?
(4)x取何值时, y1>y2
(5)你能求出函数y1=2x-4,y2=-2x+8的图象与x轴所围成的三角形的面积吗?写出过程.
随堂演练
1、在一次函数y=2x-3中,该函数与y轴的交点是________;若点P到x轴距离为2,则点P的坐标是_______________
2、当自变量x 时,函数y=3x+2的值大于0;当x 时,函数y=3x+2的值y>0 ? y≤-2?
3、如图,直线 经过点 和点 ,直线
过点A,则不等式 的解集为_________
一次函数、一元一次方程和一元一次不等式作业 姓名
1、如图,直线是一次函数的图象,观察图象,可知:
(1) ; ,函数y=
(2)当 时,y>0;
当 时,y<0,
当 时,y=0;
(3)当时, ;当y<-4时,
2、在一次函数中,已知则 ;若已知则 ;
3、当自变量 时,函数的值大于0;当 时,函数的值小于0。
4、已知函数,当 时,;当 时,。
5、已知函数y1 = 2 x – 4与y2 = - 2 x + 8的图象,观察图象并回答问题:
当 时,2x-4>0
当 时,-2x+8>0
当 时,2x-4>0与-2x+8>0同时成立?
(4)出函数y1 = 2 x – 4与y2 = - 2 x + 8的交点坐标
P (____ ,____ );图象与X轴所围成的三角形的面积 ;
(5)当 时, ;当 时,>;
当 时 <
6、 时,-2 ≤y≤5.
二、解答题
7、 某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如右下图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x30,y与x之间的函数关系式为________________;
(2)若小李4月份上网20小时,他应付 元的上网费用;
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是 小时
(4)若小李每月上网费用不想超过75元,则该如何安排上网时间?
8、一艘轮船以20km/h的速度从甲港驶 ( http: / / www.21cnjy.com )往160km远的乙港,2h后,一艘快艇以40km/h的速度也从甲港驶往乙港。分别列出轮船和快艇行驶的路程y km与时间x h的函数关系式,并在直角坐标系中画出函数的图象,观察图象回答下列问题:
何时轮船行驶在快艇的前面?
何时快艇行驶在轮船的前面?
哪一艘船先驶过60km?哪一艘船先驶过100km?。
x
y
5 10 15 20
O
10
20
30
x
2
4
2
4
6
8
-2
-2
y
班级 姓名
一 、学习目标
1、经历实际问题中数量关系的分析、抽象,得出一元一次不等式与一元一次方程、一次函数的内在联系
2、会利用不等式、方程、函数的内在联系解决问题
3.根据具体的问题情景,选用合适的工具进行解决问题;
4、通过解决实际问题,知道数学与人类生活的密切联系以及对人类历史发展的作用.并以此激发学习数学的信心和兴趣.
二 、学习重点:一元一次不等式与一元一次方程、一次函数的内在联系
三、学习难点:根据情景中所表达的关系,选用合适的工具解决问题
四、学习过程
一、情境引入:
一根长20cm的弹簧,一端固定,另一端挂物体。在弹簧伸长后的长度不超过30cm的限度内,每挂1㎏质量的物体,弹簧伸长0.5cm.如果所挂物体的质量为x㎏,弹簧的长度是ycm。 (1)求y与x之间的函数关系式,并画出函数的图象。(2)求弹簧所挂物体的最大质量是多少?
二、概括总结:
三、例1 :某人点燃一根长25cm的蜡烛,已知蜡烛每小时缩短5cm,设x h后蜡烛剩下的长度为y cm.
(1)求y与x之间的函数关系式.
(2)几小时后,蜡烛的长度不足10cm?
四、练习一:
1.x取什么值时,函数y=-2(x+1)+4的值 是正数?负数?非负数?大于6?
2. 声音在空气中的传播速度y (m/s)(简称音速)与气温x(℃)满足
关系式 .。求
(1)音速为340m/s时的气温(2)音速超过340m/s时的气温范围
五.例2 :兄弟俩赛跑,哥哥先让弟弟跑9 m,然后自己才开始跑,已知弟弟每秒跑3 m,哥哥每秒跑4 m,列出函数关系式,回答下列问题:
(1)何时弟弟跑在哥哥前面?(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20 m?谁先跑过100 m?
六. 练习二
作出函数y1=2x-4与y2=-2x+8的图象,并观察图象回答下列问题:
(1)x取何值时,y1>0?
(2)x取何值时,y2>0
(3)x取何值时,y1>0与y2>0同时成立?
(4)x取何值时, y1>y2
(5)你能求出函数y1=2x-4,y2=-2x+8的图象与x轴所围成的三角形的面积吗?写出过程.
随堂演练
1、在一次函数y=2x-3中,该函数与y轴的交点是________;若点P到x轴距离为2,则点P的坐标是_______________
2、当自变量x 时,函数y=3x+2的值大于0;当x 时,函数y=3x+2的值y>0 ? y≤-2?
3、如图,直线 经过点 和点 ,直线
过点A,则不等式 的解集为_________
一次函数、一元一次方程和一元一次不等式作业 姓名
1、如图,直线是一次函数的图象,观察图象,可知:
(1) ; ,函数y=
(2)当 时,y>0;
当 时,y<0,
当 时,y=0;
(3)当时, ;当y<-4时,
2、在一次函数中,已知则 ;若已知则 ;
3、当自变量 时,函数的值大于0;当 时,函数的值小于0。
4、已知函数,当 时,;当 时,。
5、已知函数y1 = 2 x – 4与y2 = - 2 x + 8的图象,观察图象并回答问题:
当 时,2x-4>0
当 时,-2x+8>0
当 时,2x-4>0与-2x+8>0同时成立?
(4)出函数y1 = 2 x – 4与y2 = - 2 x + 8的交点坐标
P (____ ,____ );图象与X轴所围成的三角形的面积 ;
(5)当 时, ;当 时,>;
当 时 <
6、 时,-2 ≤y≤5.
二、解答题
7、 某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如右下图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x30,y与x之间的函数关系式为________________;
(2)若小李4月份上网20小时,他应付 元的上网费用;
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是 小时
(4)若小李每月上网费用不想超过75元,则该如何安排上网时间?
8、一艘轮船以20km/h的速度从甲港驶 ( http: / / www.21cnjy.com )往160km远的乙港,2h后,一艘快艇以40km/h的速度也从甲港驶往乙港。分别列出轮船和快艇行驶的路程y km与时间x h的函数关系式,并在直角坐标系中画出函数的图象,观察图象回答下列问题:
何时轮船行驶在快艇的前面?
何时快艇行驶在轮船的前面?
哪一艘船先驶过60km?哪一艘船先驶过100km?。
x
y
5 10 15 20
O
10
20
30
x
2
4
2
4
6
8
-2
-2
y
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
