2023-2024学年人教版七年级下册数学第五章相交线与平行线证明题专题训练(含解析)
文档属性
| 名称 | 2023-2024学年人教版七年级下册数学第五章相交线与平行线证明题专题训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 10:17:28 | ||
图片预览

文档简介
2023-2024学年人教版七年级下册数学第五章相交线与平行线证明题专题训练
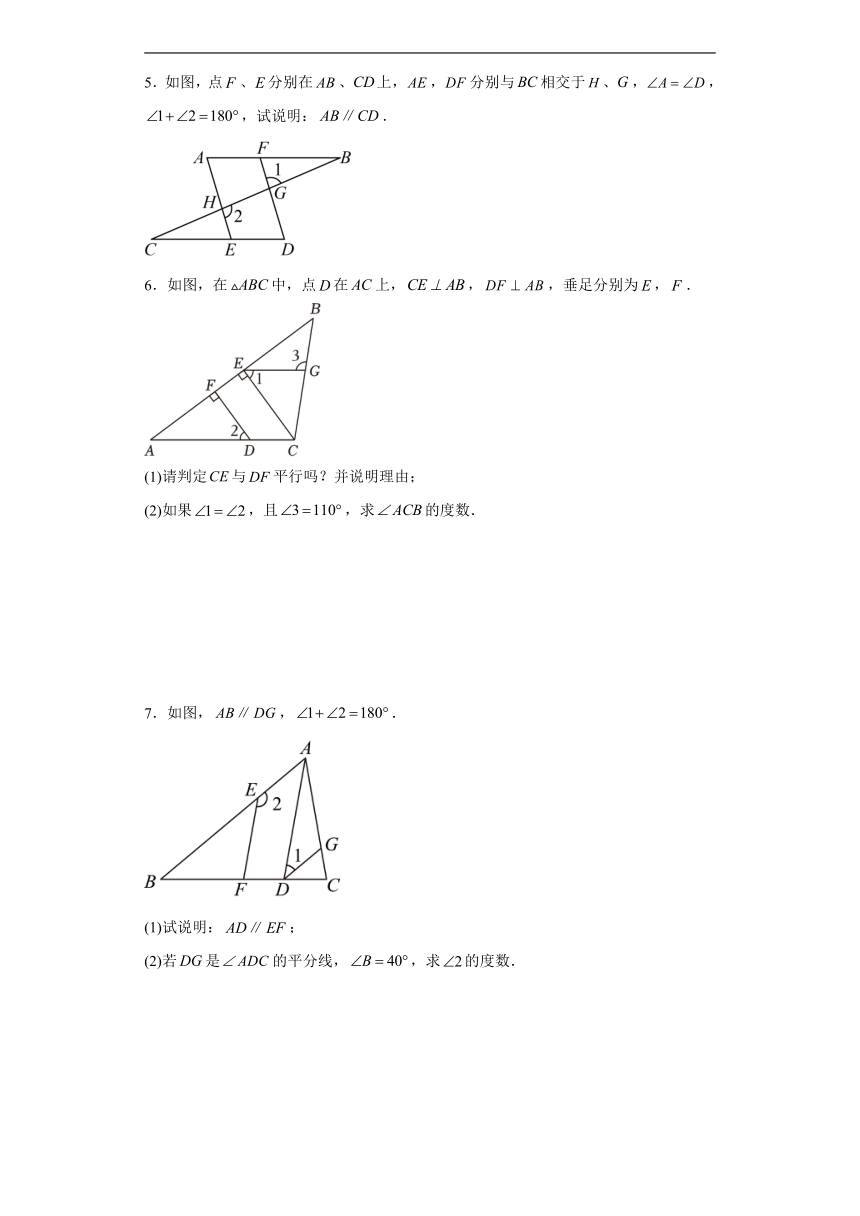
1.已知是的平分线,是的平分线,.求证:.
2.如图,AF平分,DE平分,.AB与CD有怎样的位置关系?请说明理由.
3.如图,已知点E在直线DC上,射线EF平分,过点E作,G为射线EC上一点,连接BG,且.
(1)试说明:;
(2)若,试判断AB与EF的位置关系,并说明理由.
4.如图,,试说明.
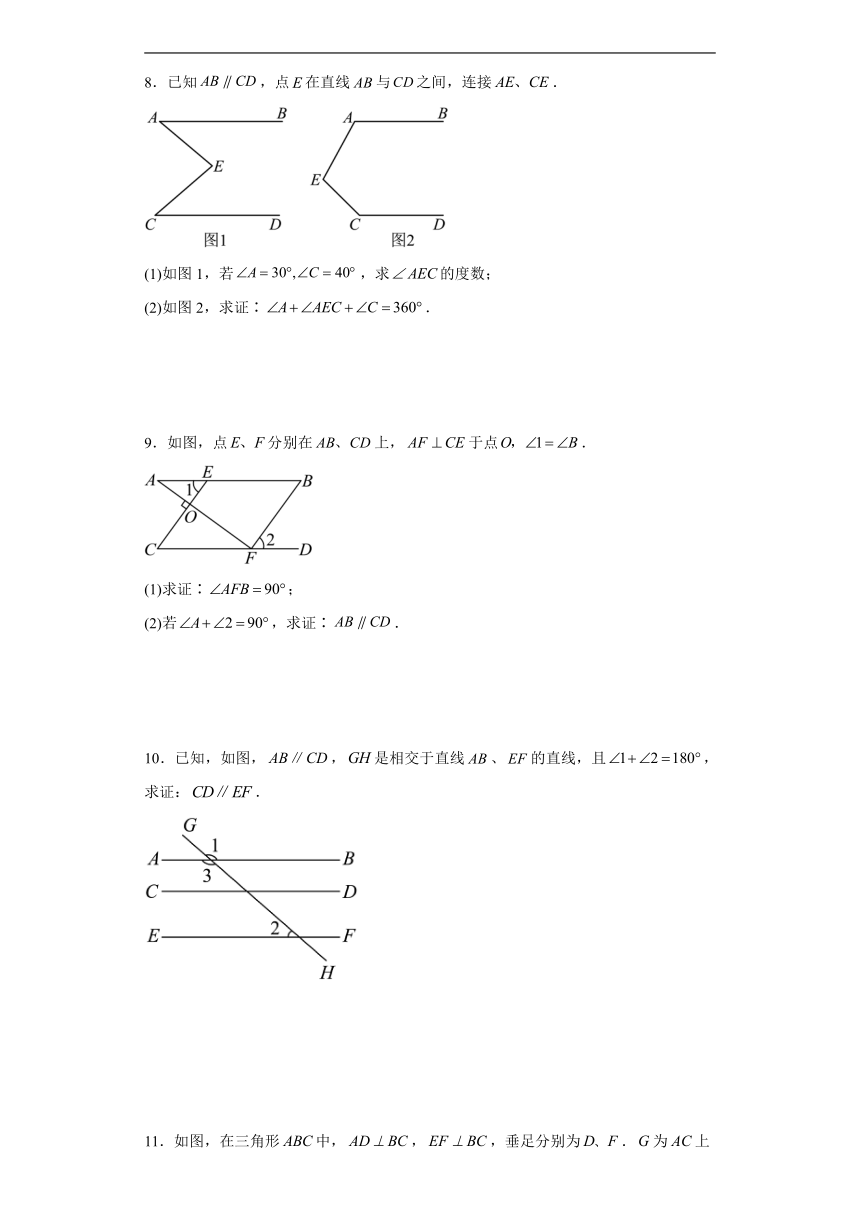
5.如图,点、分别在、上,,分别与相交于、,,,试说明:.
6.如图,在中,点在上,,,垂足分别为,.
(1)请判定与平行吗?并说明理由;
(2)如果,且,求的度数.
7.如图,,.
(1)试说明:;
(2)若是的平分线,,求的度数.
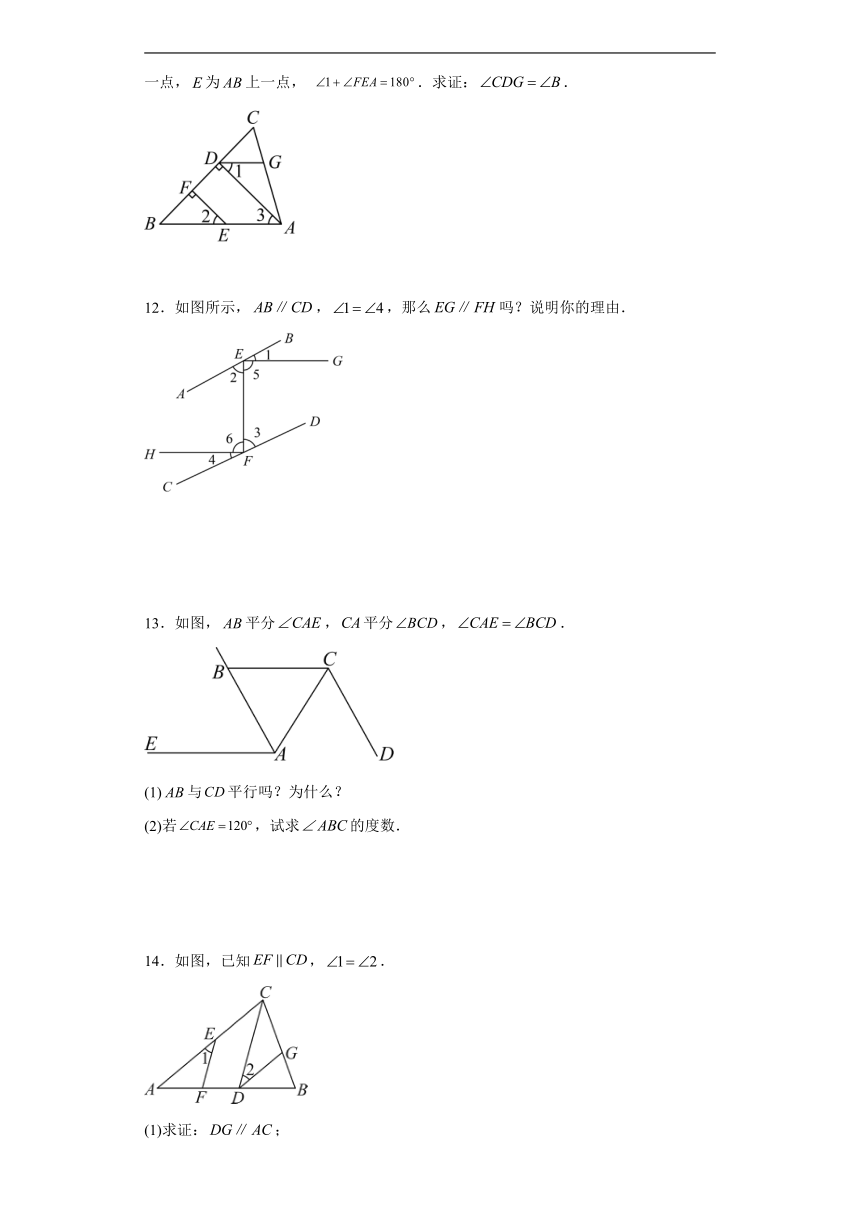
8.已知,点在直线与之间,连接.
(1)如图1,若,求的度数;
(2)如图2,求证∶.
9.如图,点分别在上,于点.
(1)求证∶;
(2)若,求证∶.
10.已知,如图,,是相交于直线、的直线,且,
求证:.
11.如图,在三角形中,,,垂足分别为.为上一点,为上一点, .求证:.
12.如图所示,,,那么吗?说明你的理由.
13.如图,平分,平分,.
(1)与平行吗?为什么?
(2)若,试求的度数.
14.如图,已知,.
(1)求证:;
(2)若平分,平分,且,求的度数.
15.如图,已知中,平分,平分,分别交、于E、F,求证:.
16.如图,E是四边形的边上一点,连接,已知,.求证:.
17.已知:如图,,和相交于点O,E是上一点,F是上一点,且.
(1)求证:;
(2)若,求的度数.
18.如图,已知.求证:
(1)
(2)
19.如图,已知.
(1)问与平行吗?如果平行请说明理由.
(2)若于E,平分,求的度数.
参考答案:
1.
【分析】本题考查了角平分线的意义和平行线的判定,熟练掌握同旁内角互补,两直线平行是解题的关键.先根据角平分线的意义得出,再根据求解即可.
【详解】∵是的平分线,是的平分线,
∴,
∵,
∴,
∴.
2..理由见解析
【详解】解:.理由如下:
因为,所以.
又因为AF平分,DE平分,
所以,,
所以,
所以.
3.(1)见解析
(2).理由见解析
【详解】解:(1)因为,所以,所以.
因为,所以.
(2).理由如下:
因为EF平分,所以.
因为,,
所以,所以,所以.
4.见解析
【分析】根据两直线平行,内错角相等得出,结合已知,得出,再根据同位角相等,两直线平行得到,最后根据两直线平行,同位角相等即可得证.
【详解】证明:,
,
,
,
,
.
【点睛】本题考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
5.见解析
【分析】根据已知得出,进而可得,则,结合已知可得,即可证明.
【详解】证明:∵,
∴,
∴,
∴,
∵,
∴,
∴.
【点睛】本题考查了平行线的性质与判定,熟练掌握平行线的性质与判定是解题的关键.
6.(1)与平行,理由见解答过程
(2)
【分析】(1)根据垂直的意义可得出,据此可得出结论;
(2)首先根据(1)的结论得出,再结合已知条件可得出,进而可判定,然后根据平行线的性质可求出的度数.
【详解】(1)解:与平行,理由如下:
,,
,
∴(垂直于同一条直线的两条直线平行).
(2)由(1)可知: ,
,
,
,
∴,
.
【点睛】此题主要考查了平行线的判定和性质,解答此题的关键是准确识图,熟练掌握平行线的判定及性质:两直线平行同位角相等,两直线平行内错角相等,两直线平行同旁内角互补.
7.(1)见详解
(2)
【分析】(1)利用平行线的性质和判定即可;
(2)结合角平分线的定义以及平行线的性质得出答案.
【详解】(1)证明:,
,
,
,
.
(2)解:,
,
是的平分线,
,
,
.
【点睛】本题考查了平行线的判定与性质,角平分线的定义,熟记平行线的性质与判定方法是解题的关键.
8.(1)
(2)见解析
【分析】(1)过点E作,根据平行线的判定得出,根据平行线的性质及角的和差求解即可;
(2)根据平行线的判定得出AB∥CD∥EF,根据平行线的性质及角的和差求解即可.
【详解】(1)如图1,过点E作,
∴,
∵,,
∴,
∴,
∵,
∴
∵,
∴;
(2)如图2,过点E作,
∴,
∵,
∴,
∴,
∴,
∴.
【点睛】此题考查了平行线的判定与性质,熟记平行线的判定与性质是解题的关键.
9.(1)见解析
(2)见解析
【分析】(1)先证得,由得;
(2)利用平角定义得出,结合可以得出,从而得证.
【详解】(1)∵,
∴,
∴,
∵,
∴,
∴;
(2)∵,
∴,
∵,
∴,
∴.
【点睛】本题主要考查平行线的判定与性质,解题的关键是掌握平行线的判定和性质,并灵活运用.
10.证明见解析
【分析】根据对顶角相等可得,,推得,根据平行线的性质可得,根据平行公理即可证明.
【详解】证明:∵,,
∴,
∴,
又∵,
∴.
【点睛】本题考查了对顶角相等,平行线的判定,平行公理,熟练掌握平行线的判定和平行公理是解题的关键.
11.证明过程见详解
【分析】根据平行线的判定和性质即可求解.
【详解】解:∵,,
∴(垂直于同一条直线的两条直线相互平行),
∴(两直线平行,同位角相等),(两直线平行,同旁内角和互补),
∵,
∴(等了代换),
∴(内错角相等,两直线平行),
∴(两直线平行,同位角相等).
【点睛】本题主要考查平行线的判定和性质,掌握其判定方法及性质的运用是解题的关键.
12.平行,见解析
【分析】先证明,再证明,即可得到答案.
【详解】证明:,
∵,
∴.
即
∵,
∴,
∴,
【点睛】本题主要考查平行线的判定与性质,掌握平行线的性质是解题的关键,
13.(1),理由见解析.
(2)
【分析】(1)根据角平分线的定义,可求得,即可判断与是否平行.
(2)根据平行线的性质,即可求得答案.
【详解】(1),理由如下:
∵平分,平分,
∴,.
∵,
∴.
∴.
(2)解:∵,,
∴
∵,
∴.
【点睛】本题主要考查平行线的判定、角平分线的定义、掌握平行线的性质与判定是解题的关键.
14.(1)见解析
(2)
【分析】(1)利用同旁内角互补,说明;
(2)由得,,由角平分线性质可求得,即可求出答案.
【详解】(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵平分,
∴,
∵,
∴,
∵平分,
∴
∵,
∴,
∴;
【点睛】本题考查了平行线的判定和性质以及角平分线的性质,把角平分线和平行线连接起来,是解决本题的关键.
15.见解析
【分析】根据平行四边形的性质得出,,再根据角平分线的定义得出,进而得出,则,得出四边形是平行四边形,即可求证.
【详解】证明:∵四边形是平行四边形,
∴,,
∵平分,平分,
∴,
∴,
∵,
∴,
∴,
∴,
∴四边形是平行四边形,
∴.
【点睛】本题主要考查了平行四边形的性质和判定,解题的关键是掌握平行四边形对边互相平行且相等,对角相等;两组对边分别平行的四边形是平行四边形.
16.见解析
【分析】根据平行线的性质与判定即可求证.
【详解】证明:∵
∴
∵
∴
∴
∴
∵
∴
∴
∴
【点睛】本题综合考查平行线的判定与性质.掌握平行线的判定与性质定理是解题关键.
17.(1)见解析
(2)
【分析】(1)根据平行线的性质可得,等量代换可得,根据平行线的判定定理即可得证;
(2)过点作,根据平行线的性质与判定可得,,根据即可求解.
【详解】(1)解:,
,
,
,
;
(2)如图,过点作,
,
,,
,
.
【点睛】本题考查了平行线的性质与判定,掌握平行线的性质与判定是解题的关键.
18.(1)见解析
(2)见解析
【分析】(1)根据平行线的性质得出,根据已知,可得,进而可得;
(2)根据平行线的性质以及已知条件得出,进而结合图形,即可求解.
【详解】(1)证明:(已知)
(两直线平行,同位角相等)
∵(已知)
∴(等量代换)
∴(内错角相等,两直线平行))
(2)(已知)
(两直线平行,内错角相等)
(已知)
(两直线平行,同位角相等)
(已知)
(等量代换)
,
,
(等式的性质)
【点睛】本题考查了平行线的性质与判定,熟练掌握平行线的性质与判定是解题的关键.
19.(1),理由见解析
(2)的度数为
【点睛】(1)利用已知可得,从而可得,进而可得,然后利用同旁内角互补,两直线平行可得,即可解答;
(2)根据垂直定义可得,再利用(1)的结论可得,从而可得,然后利用(1)的结论可得,再利用角平分线的定义可得,即可解答.
【详解】(1)解:,
理由:∵,
∴,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵平分,
∴,
∴,
∴的度数为.
【点评】本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题的关键.
1.已知是的平分线,是的平分线,.求证:.
2.如图,AF平分,DE平分,.AB与CD有怎样的位置关系?请说明理由.
3.如图,已知点E在直线DC上,射线EF平分,过点E作,G为射线EC上一点,连接BG,且.
(1)试说明:;
(2)若,试判断AB与EF的位置关系,并说明理由.
4.如图,,试说明.
5.如图,点、分别在、上,,分别与相交于、,,,试说明:.
6.如图,在中,点在上,,,垂足分别为,.
(1)请判定与平行吗?并说明理由;
(2)如果,且,求的度数.
7.如图,,.
(1)试说明:;
(2)若是的平分线,,求的度数.
8.已知,点在直线与之间,连接.
(1)如图1,若,求的度数;
(2)如图2,求证∶.
9.如图,点分别在上,于点.
(1)求证∶;
(2)若,求证∶.
10.已知,如图,,是相交于直线、的直线,且,
求证:.
11.如图,在三角形中,,,垂足分别为.为上一点,为上一点, .求证:.
12.如图所示,,,那么吗?说明你的理由.
13.如图,平分,平分,.
(1)与平行吗?为什么?
(2)若,试求的度数.
14.如图,已知,.
(1)求证:;
(2)若平分,平分,且,求的度数.
15.如图,已知中,平分,平分,分别交、于E、F,求证:.
16.如图,E是四边形的边上一点,连接,已知,.求证:.
17.已知:如图,,和相交于点O,E是上一点,F是上一点,且.
(1)求证:;
(2)若,求的度数.
18.如图,已知.求证:
(1)
(2)
19.如图,已知.
(1)问与平行吗?如果平行请说明理由.
(2)若于E,平分,求的度数.
参考答案:
1.
【分析】本题考查了角平分线的意义和平行线的判定,熟练掌握同旁内角互补,两直线平行是解题的关键.先根据角平分线的意义得出,再根据求解即可.
【详解】∵是的平分线,是的平分线,
∴,
∵,
∴,
∴.
2..理由见解析
【详解】解:.理由如下:
因为,所以.
又因为AF平分,DE平分,
所以,,
所以,
所以.
3.(1)见解析
(2).理由见解析
【详解】解:(1)因为,所以,所以.
因为,所以.
(2).理由如下:
因为EF平分,所以.
因为,,
所以,所以,所以.
4.见解析
【分析】根据两直线平行,内错角相等得出,结合已知,得出,再根据同位角相等,两直线平行得到,最后根据两直线平行,同位角相等即可得证.
【详解】证明:,
,
,
,
,
.
【点睛】本题考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
5.见解析
【分析】根据已知得出,进而可得,则,结合已知可得,即可证明.
【详解】证明:∵,
∴,
∴,
∴,
∵,
∴,
∴.
【点睛】本题考查了平行线的性质与判定,熟练掌握平行线的性质与判定是解题的关键.
6.(1)与平行,理由见解答过程
(2)
【分析】(1)根据垂直的意义可得出,据此可得出结论;
(2)首先根据(1)的结论得出,再结合已知条件可得出,进而可判定,然后根据平行线的性质可求出的度数.
【详解】(1)解:与平行,理由如下:
,,
,
∴(垂直于同一条直线的两条直线平行).
(2)由(1)可知: ,
,
,
,
∴,
.
【点睛】此题主要考查了平行线的判定和性质,解答此题的关键是准确识图,熟练掌握平行线的判定及性质:两直线平行同位角相等,两直线平行内错角相等,两直线平行同旁内角互补.
7.(1)见详解
(2)
【分析】(1)利用平行线的性质和判定即可;
(2)结合角平分线的定义以及平行线的性质得出答案.
【详解】(1)证明:,
,
,
,
.
(2)解:,
,
是的平分线,
,
,
.
【点睛】本题考查了平行线的判定与性质,角平分线的定义,熟记平行线的性质与判定方法是解题的关键.
8.(1)
(2)见解析
【分析】(1)过点E作,根据平行线的判定得出,根据平行线的性质及角的和差求解即可;
(2)根据平行线的判定得出AB∥CD∥EF,根据平行线的性质及角的和差求解即可.
【详解】(1)如图1,过点E作,
∴,
∵,,
∴,
∴,
∵,
∴
∵,
∴;
(2)如图2,过点E作,
∴,
∵,
∴,
∴,
∴,
∴.
【点睛】此题考查了平行线的判定与性质,熟记平行线的判定与性质是解题的关键.
9.(1)见解析
(2)见解析
【分析】(1)先证得,由得;
(2)利用平角定义得出,结合可以得出,从而得证.
【详解】(1)∵,
∴,
∴,
∵,
∴,
∴;
(2)∵,
∴,
∵,
∴,
∴.
【点睛】本题主要考查平行线的判定与性质,解题的关键是掌握平行线的判定和性质,并灵活运用.
10.证明见解析
【分析】根据对顶角相等可得,,推得,根据平行线的性质可得,根据平行公理即可证明.
【详解】证明:∵,,
∴,
∴,
又∵,
∴.
【点睛】本题考查了对顶角相等,平行线的判定,平行公理,熟练掌握平行线的判定和平行公理是解题的关键.
11.证明过程见详解
【分析】根据平行线的判定和性质即可求解.
【详解】解:∵,,
∴(垂直于同一条直线的两条直线相互平行),
∴(两直线平行,同位角相等),(两直线平行,同旁内角和互补),
∵,
∴(等了代换),
∴(内错角相等,两直线平行),
∴(两直线平行,同位角相等).
【点睛】本题主要考查平行线的判定和性质,掌握其判定方法及性质的运用是解题的关键.
12.平行,见解析
【分析】先证明,再证明,即可得到答案.
【详解】证明:,
∵,
∴.
即
∵,
∴,
∴,
【点睛】本题主要考查平行线的判定与性质,掌握平行线的性质是解题的关键,
13.(1),理由见解析.
(2)
【分析】(1)根据角平分线的定义,可求得,即可判断与是否平行.
(2)根据平行线的性质,即可求得答案.
【详解】(1),理由如下:
∵平分,平分,
∴,.
∵,
∴.
∴.
(2)解:∵,,
∴
∵,
∴.
【点睛】本题主要考查平行线的判定、角平分线的定义、掌握平行线的性质与判定是解题的关键.
14.(1)见解析
(2)
【分析】(1)利用同旁内角互补,说明;
(2)由得,,由角平分线性质可求得,即可求出答案.
【详解】(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵平分,
∴,
∵,
∴,
∵平分,
∴
∵,
∴,
∴;
【点睛】本题考查了平行线的判定和性质以及角平分线的性质,把角平分线和平行线连接起来,是解决本题的关键.
15.见解析
【分析】根据平行四边形的性质得出,,再根据角平分线的定义得出,进而得出,则,得出四边形是平行四边形,即可求证.
【详解】证明:∵四边形是平行四边形,
∴,,
∵平分,平分,
∴,
∴,
∵,
∴,
∴,
∴,
∴四边形是平行四边形,
∴.
【点睛】本题主要考查了平行四边形的性质和判定,解题的关键是掌握平行四边形对边互相平行且相等,对角相等;两组对边分别平行的四边形是平行四边形.
16.见解析
【分析】根据平行线的性质与判定即可求证.
【详解】证明:∵
∴
∵
∴
∴
∴
∵
∴
∴
∴
【点睛】本题综合考查平行线的判定与性质.掌握平行线的判定与性质定理是解题关键.
17.(1)见解析
(2)
【分析】(1)根据平行线的性质可得,等量代换可得,根据平行线的判定定理即可得证;
(2)过点作,根据平行线的性质与判定可得,,根据即可求解.
【详解】(1)解:,
,
,
,
;
(2)如图,过点作,
,
,,
,
.
【点睛】本题考查了平行线的性质与判定,掌握平行线的性质与判定是解题的关键.
18.(1)见解析
(2)见解析
【分析】(1)根据平行线的性质得出,根据已知,可得,进而可得;
(2)根据平行线的性质以及已知条件得出,进而结合图形,即可求解.
【详解】(1)证明:(已知)
(两直线平行,同位角相等)
∵(已知)
∴(等量代换)
∴(内错角相等,两直线平行))
(2)(已知)
(两直线平行,内错角相等)
(已知)
(两直线平行,同位角相等)
(已知)
(等量代换)
,
,
(等式的性质)
【点睛】本题考查了平行线的性质与判定,熟练掌握平行线的性质与判定是解题的关键.
19.(1),理由见解析
(2)的度数为
【点睛】(1)利用已知可得,从而可得,进而可得,然后利用同旁内角互补,两直线平行可得,即可解答;
(2)根据垂直定义可得,再利用(1)的结论可得,从而可得,然后利用(1)的结论可得,再利用角平分线的定义可得,即可解答.
【详解】(1)解:,
理由:∵,
∴,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵平分,
∴,
∴,
∴的度数为.
【点评】本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题的关键.
