苏教版四年级下册数学第五单元解决问题的策略复习课(课件)(共35张PPT)
文档属性
| 名称 | 苏教版四年级下册数学第五单元解决问题的策略复习课(课件)(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览









文档简介
(共35张PPT)
苏教版 数学 四年级 下册
复习旧知
题型总结
课后作业
解决问题的策略
探索规律
复习课
用画图的策略解决实际问题
复习旧知
第五章你们都学会了哪些知识?
策略一:画线段图
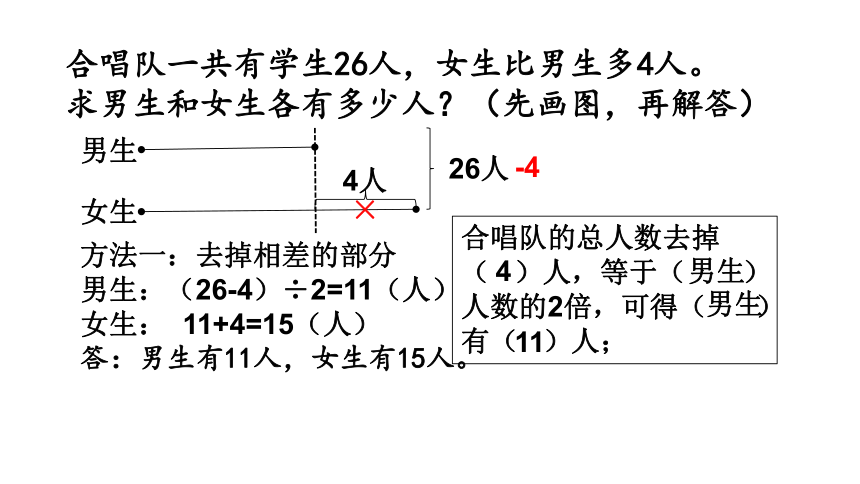
合唱队一共有学生26人,女生比男生多4人。求男生和女生各有多少人?(先画图,再解答)
男生
女生
26人
4人
方法一:去掉相差的部分
男生:(26-4)÷2=11(人)
女生: 11+4=15(人)
答:男生有11人,女生有15人。
合唱队的总人数去掉( )人,等于( )人数的2倍,可得( )有( )人;
4
男生
男生
11
×
-4
合唱队一共有学生26人,女生比男生多4人。求男生和女生各有多少人?(先画图,再解答)
男生
女生
26人
4人
方法二:补上相差的部分
女生:(26+4)÷2=15(人)
男生: 15-4=11(人)
答:男生有11人,女生有15人。
合唱队的总人数添上( )人,等于( )人数的2倍,可得( )有( )人;
4
女生
女生
15
4人
+4人
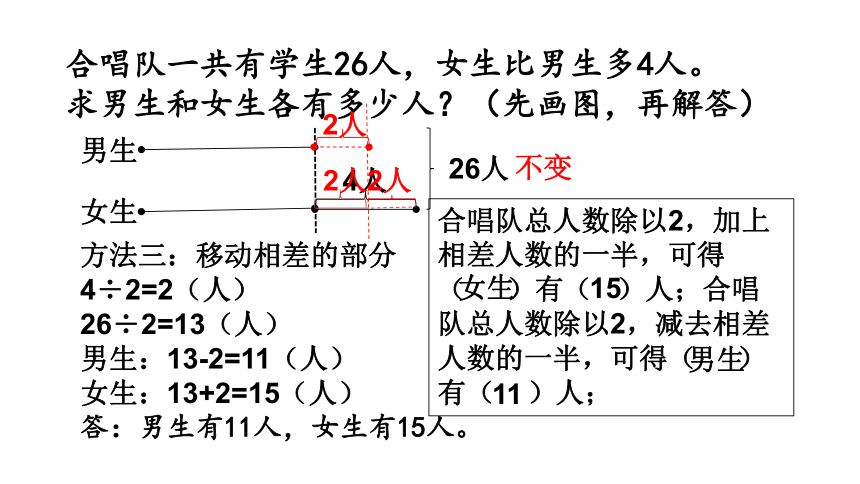
合唱队一共有学生26人,女生比男生多4人。求男生和女生各有多少人?(先画图,再解答)
男生
女生
26人
4人
方法三:移动相差的部分
4÷2=2(人)
26÷2=13(人)
男生:13-2=11(人)
女生:13+2=15(人)
答:男生有11人,女生有15人。
合唱队总人数除以2,加上相差人数的一半,可得( )有( )人;合唱队总人数除以2,减去相差人数的一半,可得( )有( )人;
2人
不变
2人
2人
女生
15
男生
11
同步练习
检验:
11+15=26(人)
15-11=4(人)
规律总结(只有两个量):
1.总和去掉相差的部分,变成两个相同的少(短线段)的量,可先求得少(短线段)的量。
2.总和加上相差的部分,变成两个相同的多(长线段)的量,可先求得多(长线段)的量。
3.总和不变,移动相差的部分,平均分给各个量,使得各个量一样多,再求各个量,多(长线段)的量就是总和平均数加移动部分,少(短线段)的量就是总和平均数减移动部分。
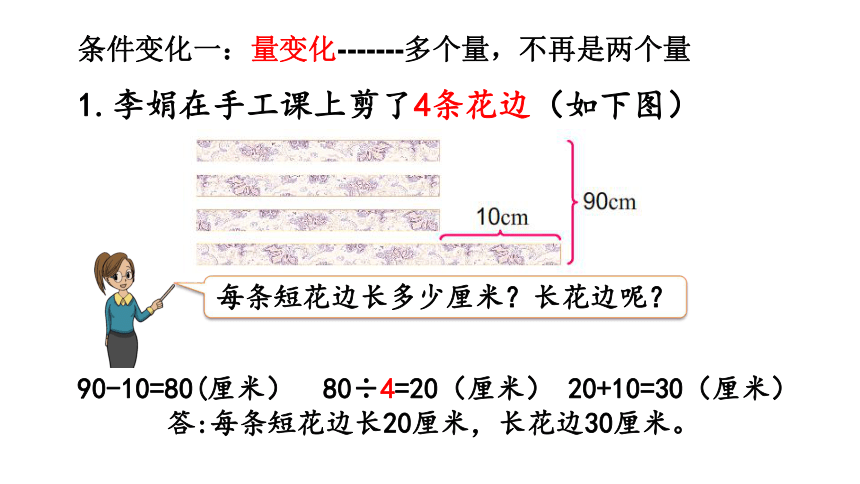
1.李娟在手工课上剪了4条花边(如下图)
每条短花边长多少厘米?长花边呢?
90-10=80(厘米) 80÷4=20(厘米) 20+10=30(厘米)
答:每条短花边长20厘米,长花边30厘米。
条件变化一:量变化-------多个量,不再是两个量
条件变化二:总和表述变化------不直接给出总和,给出总和的倍数或者一半等等
1.有一块长方形菜地,它的周长是76米,长比宽多8米,这块长方形菜地的长、宽各是多少米?(先画图,再解答)
2.小明期末考试时语文和数学的平均分是94分,数学比语文多8分,语文和数学的得分分别是多少分?(先画图,再解答)
长和宽的总和——76÷2
语文和数学的总分——94×2
条件变化三:相差的部分表述变化——相差的部分不直接表述,换形式表述;存在多个相差部分
1.张伟和浩浩一共收集了220枚邮票,如果浩浩再收集30枚邮票则和张伟同样多,原来张伟和浩浩各收集了多少枚邮票?(先画图,再解答)
张伟比浩浩多30枚邮票
2.张伟和浩浩一共收集了220枚邮票,如果张伟给浩浩30枚邮票,则两人同样多,原来张伟和浩浩各收集了多少枚邮票?(先画图,再解答)
张伟比浩浩多60枚邮票
3.小明和小芳共有98本连环画,如果小明给小芳10本,那么小明还比小芳多2本。小明和小芳各有多少本连环画。
小明比小芳多22本
4.甲、乙两个鱼缸里共有金鱼25条,甲鱼缸里重新放入6条,乙鱼缸里取出4条,这时乙鱼缸比甲鱼缸还多5条。甲、乙两个鱼缸原来各有多少条金鱼?
乙鱼缸比甲鱼缸多15条鱼
5.甲、乙两船共有乘客623人,如果甲船增加34人,乙船减少57人,那么两船的乘客同样多,求乙船有乘客多少人?
乙船比甲船多91人
3.某工厂将875元奖金分别给创造发明的三名优秀工人。第一名比第二名多250元,第二名比第三名多得125元,三名优秀工人各得多少元?
第一名:
第二名:
第三名:
875元
250元
125元
?
第一名比第三名多250+125=375元
第三名的钱是[875-(250+125)-125]/3=125元
第二名就是125+125=250元
第一名就是250+125+125=500元
条件变化四:不给出各个量的总和,而是给出各个量之间的倍数关系、数量关系······
1.一个养鸡场,养的公鸡比母鸡少240只,母鸡的只数正好是公鸡的4倍,这个养鸡场养的公鸡和母鸡各有多少只?
2.小建和小西买同样的笔记本,小建买了3本,小西买了5本,小建比小西少花12元。小建和小西各花了多少钱?
问题变化:不直接求问各个量的值
有一块长方形菜地,它的周长是76米,长比宽多8米,这块长方形菜地面积是多少平方米?(先画图,再解答)
题型变化:结合第三单元公式出题······
小建和小西买同样的笔记本,小建买了3本,小西买了5本,小建比小西少花12元。笔记本单价是多少元/本?
总价=单价×数量
甲、乙两地相距495千米,一辆汽车从甲地开往乙地,已经行了3小时,剩下的路程比已经行的多45千米。这辆汽车的平均速度是多少千米/时?
路程=速度×时间
混合变化:各种变化混合一起
1.一个双层书架,上层书的本数是下层的3倍。如果从上层搬60本到下层,那么两层书的本数正好相等。原来上、下层各有图书多少本?(先画图,再解答)
2.甲、乙两箱一共有水果54千克,若从甲箱取出6千克放入乙箱,乙箱的水果恰好是甲箱的2倍。两箱原来各有水果多少千克?(先画图,再解答)
3.甲、乙两个冷藏室共存鸡蛋1260箱,从甲冷藏室运走250箱后,乙冷藏库存的鸡蛋箱数比甲冷藏库剩下的鸡蛋箱数的4倍还多80箱。甲、乙两个冷藏库原来各有鸡蛋多少箱?
策略二:画示意图
1.一个长方形花圃,长8米,如果苗圃的长增加3米,面积就增加18平方米。苗圃原来的面积是多少平方米?
8米
3米
18平方米
?平方米
1.要求原来苗圃的面积,要先算它的( )。
2.原来苗圃的( ),就是新增的小长方形的( )。
3.增加的面积是18平方米,宽是3米,可求得它的长是( )米
宽是多少米
宽
长
6
宽:18÷3=6(米)
原来的面积:6×8=48(平方米)
2.一个长方形花圃,宽6米,如果苗圃的宽减少3米,面积就减少24平方米。苗圃原来的面积是多少平方米?
6米
3米
24平方米
1.要求原来苗圃的面积,要先算它的( )。
2.原来苗圃的( ),就是减少的小长方形的( )。
3.减少的面积是24平方米,宽是3米,可求得它的长是( )米
长是多少米
长
长
8
长:24÷3=8(米)
原来的面积:6×8=48(平方米)
新庄小学的操场原来是一个正方形。扩建校园时,操场的一组对边各增加18米,这样操场的面积就增加了900平方米。原来操场的面积是多少平方米?(先在图上画一画,再解答)
增加900
平方米
18米
900÷18=50(米)
50×50=2500(平方米)
答:原来操场的面积
是2500平方米。
平方米
变化一:图形变化——长方形变为正方形
规律总结:
1.长方形长变化了,原长方形的宽不变
2.长方形宽变化了,原长方形的长不变
3.正方形一组对边变化了,原正方形的另一组对边不变。
一组对边变化,对应原图形的另一组对边不变
??????
1.将一个长方形的长增加5厘米或宽增加3厘米后,面积都增加60平方厘米,原来这个长方形的面积是多少?(先画图整理条件和问题,再解答。)
5厘米
3厘米
60平方厘米
60平方厘米
平方厘米
宽:60÷5=12(厘米)
长:60÷3=20(厘米)
原来长方形面积:12×20=240(平方厘米)
变化二:长和宽的变化都出现在同一题中
2.张庄小学原来有一个长方形操场,长50米,宽40米。扩建校园时,操场的长增加了10米,宽增加了8米。操场
的面积增加了多少平方米?
原操场面积
50米
40米
8米
10米
平方米
平方米
8×(50+10)=480(平方米)
10×40=400(平方米)
480+400=880(平方米)
答:操场的面积增加了880平方米。
思考一下:上述两题如果增加都变为减少,几何图又该如何画?
3.一个正方形,如果它的边长增加5米,得到的正方形比原来正方形的面积多95平方米,原来正方形的边长为多少米?(先画出示意图,再解答)
5米
5米
95平方米
5×5=25(平方米)
95-25=70(平方米)
70÷2=35(平方米)
35÷5=7(米)
1.有一个长60米、宽40米的长方形鱼塘,如果要把它扩建成正方形鱼塘,面积至少增加多少平方米?
60×60-60×40
=3600-2400
=1200(平方米)
答:面积至少增加1200平方米。
变化三:长方形如何变正方形
将长方形的宽增加到和长一样的长度,此时得到的正方形边长即为原长方形的长。
60米
40米
60米
2.王晓芳有一张宽30厘米的长方形彩纸,她从这张彩纸上裁下一个最大的正方形小旗,剩下彩纸的面积是360平方厘米。原来彩纸的面积是多少平方厘米?
30×30+360
=900+360
=1260(平方米)
答:原来彩纸的面积是1260平方厘米。
将长方形的长减少到和宽一样的长度,此时得到的正方形边长即为原长方形的宽。
30厘米
30厘米
360平方厘米
3.有一张长方形彩纸,从这张彩纸上剪下一个最大的正方形后,剩下的彩纸形状如下图,原来这张彩纸的面积可能是多少?
30厘米
20厘米
第一种可能:剪下的最大正方形以20厘米为边长。
(20+30)×20=1000(平方厘米)
第二种可能:剪下的最大正方形以30厘米为边长。
(20+30)×30=1500(平方厘米)
变化四:修路问题——切割成几个规则图形
1.赵大伯家有一块边长为50米的正方形菜地,如果在菜地内修一条宽2米的小路(如下图),修完这条小路后,菜地的面积是多少平方米
2米
4.王大爷家有一个边长是30米的正方形鱼塘。王大爷计划在鱼塘的四周修一条宽2米的小路,这条小路的占地面积是多少平方米?
30米
鱼塘
2米
2米
1.一个长方形菜园,种黄瓜的面积比菜园的一半还要多8平方米,其余的14平方米种番茄,这个菜园有多少平方米
8平方米
14平方米
菜园面积的一半:8+14=22平方米
菜园面积:22×2=44平方米
变化五:菜园子问题——分清楚哪部分是菜园子的一半
2.一块长方形地,种大豆的面积比整块地的一半少300平方米,其余的1200平方米种玉米,这块地的面积是多少平方米?(先画出示意图,再解答)
大豆
玉米
菜园的一半:
(1200-300)=900(平方米)
菜园面积:900×2=1800(平方米)
变化六:问题变化
1.求原来图形的面积:①求出原来图形的长和宽(边长);②现在的面积减增加的面积或者现在的面积加减少的面积。
2.求现在图形的面积:①求出现在图形的长和宽(边长);②原来的面积加增加的面积或者原来的面积减减少的面积。
3.求增加或者减少的面积:①求出增加或者减少部分的规则图形的长和宽(边长);②现在的面积与原来的面积相加减
感谢观看
苏教版 数学 四年级 下册
复习旧知
题型总结
课后作业
解决问题的策略
探索规律
复习课
用画图的策略解决实际问题
复习旧知
第五章你们都学会了哪些知识?
策略一:画线段图
合唱队一共有学生26人,女生比男生多4人。求男生和女生各有多少人?(先画图,再解答)
男生
女生
26人
4人
方法一:去掉相差的部分
男生:(26-4)÷2=11(人)
女生: 11+4=15(人)
答:男生有11人,女生有15人。
合唱队的总人数去掉( )人,等于( )人数的2倍,可得( )有( )人;
4
男生
男生
11
×
-4
合唱队一共有学生26人,女生比男生多4人。求男生和女生各有多少人?(先画图,再解答)
男生
女生
26人
4人
方法二:补上相差的部分
女生:(26+4)÷2=15(人)
男生: 15-4=11(人)
答:男生有11人,女生有15人。
合唱队的总人数添上( )人,等于( )人数的2倍,可得( )有( )人;
4
女生
女生
15
4人
+4人
合唱队一共有学生26人,女生比男生多4人。求男生和女生各有多少人?(先画图,再解答)
男生
女生
26人
4人
方法三:移动相差的部分
4÷2=2(人)
26÷2=13(人)
男生:13-2=11(人)
女生:13+2=15(人)
答:男生有11人,女生有15人。
合唱队总人数除以2,加上相差人数的一半,可得( )有( )人;合唱队总人数除以2,减去相差人数的一半,可得( )有( )人;
2人
不变
2人
2人
女生
15
男生
11
同步练习
检验:
11+15=26(人)
15-11=4(人)
规律总结(只有两个量):
1.总和去掉相差的部分,变成两个相同的少(短线段)的量,可先求得少(短线段)的量。
2.总和加上相差的部分,变成两个相同的多(长线段)的量,可先求得多(长线段)的量。
3.总和不变,移动相差的部分,平均分给各个量,使得各个量一样多,再求各个量,多(长线段)的量就是总和平均数加移动部分,少(短线段)的量就是总和平均数减移动部分。
1.李娟在手工课上剪了4条花边(如下图)
每条短花边长多少厘米?长花边呢?
90-10=80(厘米) 80÷4=20(厘米) 20+10=30(厘米)
答:每条短花边长20厘米,长花边30厘米。
条件变化一:量变化-------多个量,不再是两个量
条件变化二:总和表述变化------不直接给出总和,给出总和的倍数或者一半等等
1.有一块长方形菜地,它的周长是76米,长比宽多8米,这块长方形菜地的长、宽各是多少米?(先画图,再解答)
2.小明期末考试时语文和数学的平均分是94分,数学比语文多8分,语文和数学的得分分别是多少分?(先画图,再解答)
长和宽的总和——76÷2
语文和数学的总分——94×2
条件变化三:相差的部分表述变化——相差的部分不直接表述,换形式表述;存在多个相差部分
1.张伟和浩浩一共收集了220枚邮票,如果浩浩再收集30枚邮票则和张伟同样多,原来张伟和浩浩各收集了多少枚邮票?(先画图,再解答)
张伟比浩浩多30枚邮票
2.张伟和浩浩一共收集了220枚邮票,如果张伟给浩浩30枚邮票,则两人同样多,原来张伟和浩浩各收集了多少枚邮票?(先画图,再解答)
张伟比浩浩多60枚邮票
3.小明和小芳共有98本连环画,如果小明给小芳10本,那么小明还比小芳多2本。小明和小芳各有多少本连环画。
小明比小芳多22本
4.甲、乙两个鱼缸里共有金鱼25条,甲鱼缸里重新放入6条,乙鱼缸里取出4条,这时乙鱼缸比甲鱼缸还多5条。甲、乙两个鱼缸原来各有多少条金鱼?
乙鱼缸比甲鱼缸多15条鱼
5.甲、乙两船共有乘客623人,如果甲船增加34人,乙船减少57人,那么两船的乘客同样多,求乙船有乘客多少人?
乙船比甲船多91人
3.某工厂将875元奖金分别给创造发明的三名优秀工人。第一名比第二名多250元,第二名比第三名多得125元,三名优秀工人各得多少元?
第一名:
第二名:
第三名:
875元
250元
125元
?
第一名比第三名多250+125=375元
第三名的钱是[875-(250+125)-125]/3=125元
第二名就是125+125=250元
第一名就是250+125+125=500元
条件变化四:不给出各个量的总和,而是给出各个量之间的倍数关系、数量关系······
1.一个养鸡场,养的公鸡比母鸡少240只,母鸡的只数正好是公鸡的4倍,这个养鸡场养的公鸡和母鸡各有多少只?
2.小建和小西买同样的笔记本,小建买了3本,小西买了5本,小建比小西少花12元。小建和小西各花了多少钱?
问题变化:不直接求问各个量的值
有一块长方形菜地,它的周长是76米,长比宽多8米,这块长方形菜地面积是多少平方米?(先画图,再解答)
题型变化:结合第三单元公式出题······
小建和小西买同样的笔记本,小建买了3本,小西买了5本,小建比小西少花12元。笔记本单价是多少元/本?
总价=单价×数量
甲、乙两地相距495千米,一辆汽车从甲地开往乙地,已经行了3小时,剩下的路程比已经行的多45千米。这辆汽车的平均速度是多少千米/时?
路程=速度×时间
混合变化:各种变化混合一起
1.一个双层书架,上层书的本数是下层的3倍。如果从上层搬60本到下层,那么两层书的本数正好相等。原来上、下层各有图书多少本?(先画图,再解答)
2.甲、乙两箱一共有水果54千克,若从甲箱取出6千克放入乙箱,乙箱的水果恰好是甲箱的2倍。两箱原来各有水果多少千克?(先画图,再解答)
3.甲、乙两个冷藏室共存鸡蛋1260箱,从甲冷藏室运走250箱后,乙冷藏库存的鸡蛋箱数比甲冷藏库剩下的鸡蛋箱数的4倍还多80箱。甲、乙两个冷藏库原来各有鸡蛋多少箱?
策略二:画示意图
1.一个长方形花圃,长8米,如果苗圃的长增加3米,面积就增加18平方米。苗圃原来的面积是多少平方米?
8米
3米
18平方米
?平方米
1.要求原来苗圃的面积,要先算它的( )。
2.原来苗圃的( ),就是新增的小长方形的( )。
3.增加的面积是18平方米,宽是3米,可求得它的长是( )米
宽是多少米
宽
长
6
宽:18÷3=6(米)
原来的面积:6×8=48(平方米)
2.一个长方形花圃,宽6米,如果苗圃的宽减少3米,面积就减少24平方米。苗圃原来的面积是多少平方米?
6米
3米
24平方米
1.要求原来苗圃的面积,要先算它的( )。
2.原来苗圃的( ),就是减少的小长方形的( )。
3.减少的面积是24平方米,宽是3米,可求得它的长是( )米
长是多少米
长
长
8
长:24÷3=8(米)
原来的面积:6×8=48(平方米)
新庄小学的操场原来是一个正方形。扩建校园时,操场的一组对边各增加18米,这样操场的面积就增加了900平方米。原来操场的面积是多少平方米?(先在图上画一画,再解答)
增加900
平方米
18米
900÷18=50(米)
50×50=2500(平方米)
答:原来操场的面积
是2500平方米。
平方米
变化一:图形变化——长方形变为正方形
规律总结:
1.长方形长变化了,原长方形的宽不变
2.长方形宽变化了,原长方形的长不变
3.正方形一组对边变化了,原正方形的另一组对边不变。
一组对边变化,对应原图形的另一组对边不变
??????
1.将一个长方形的长增加5厘米或宽增加3厘米后,面积都增加60平方厘米,原来这个长方形的面积是多少?(先画图整理条件和问题,再解答。)
5厘米
3厘米
60平方厘米
60平方厘米
平方厘米
宽:60÷5=12(厘米)
长:60÷3=20(厘米)
原来长方形面积:12×20=240(平方厘米)
变化二:长和宽的变化都出现在同一题中
2.张庄小学原来有一个长方形操场,长50米,宽40米。扩建校园时,操场的长增加了10米,宽增加了8米。操场
的面积增加了多少平方米?
原操场面积
50米
40米
8米
10米
平方米
平方米
8×(50+10)=480(平方米)
10×40=400(平方米)
480+400=880(平方米)
答:操场的面积增加了880平方米。
思考一下:上述两题如果增加都变为减少,几何图又该如何画?
3.一个正方形,如果它的边长增加5米,得到的正方形比原来正方形的面积多95平方米,原来正方形的边长为多少米?(先画出示意图,再解答)
5米
5米
95平方米
5×5=25(平方米)
95-25=70(平方米)
70÷2=35(平方米)
35÷5=7(米)
1.有一个长60米、宽40米的长方形鱼塘,如果要把它扩建成正方形鱼塘,面积至少增加多少平方米?
60×60-60×40
=3600-2400
=1200(平方米)
答:面积至少增加1200平方米。
变化三:长方形如何变正方形
将长方形的宽增加到和长一样的长度,此时得到的正方形边长即为原长方形的长。
60米
40米
60米
2.王晓芳有一张宽30厘米的长方形彩纸,她从这张彩纸上裁下一个最大的正方形小旗,剩下彩纸的面积是360平方厘米。原来彩纸的面积是多少平方厘米?
30×30+360
=900+360
=1260(平方米)
答:原来彩纸的面积是1260平方厘米。
将长方形的长减少到和宽一样的长度,此时得到的正方形边长即为原长方形的宽。
30厘米
30厘米
360平方厘米
3.有一张长方形彩纸,从这张彩纸上剪下一个最大的正方形后,剩下的彩纸形状如下图,原来这张彩纸的面积可能是多少?
30厘米
20厘米
第一种可能:剪下的最大正方形以20厘米为边长。
(20+30)×20=1000(平方厘米)
第二种可能:剪下的最大正方形以30厘米为边长。
(20+30)×30=1500(平方厘米)
变化四:修路问题——切割成几个规则图形
1.赵大伯家有一块边长为50米的正方形菜地,如果在菜地内修一条宽2米的小路(如下图),修完这条小路后,菜地的面积是多少平方米
2米
4.王大爷家有一个边长是30米的正方形鱼塘。王大爷计划在鱼塘的四周修一条宽2米的小路,这条小路的占地面积是多少平方米?
30米
鱼塘
2米
2米
1.一个长方形菜园,种黄瓜的面积比菜园的一半还要多8平方米,其余的14平方米种番茄,这个菜园有多少平方米
8平方米
14平方米
菜园面积的一半:8+14=22平方米
菜园面积:22×2=44平方米
变化五:菜园子问题——分清楚哪部分是菜园子的一半
2.一块长方形地,种大豆的面积比整块地的一半少300平方米,其余的1200平方米种玉米,这块地的面积是多少平方米?(先画出示意图,再解答)
大豆
玉米
菜园的一半:
(1200-300)=900(平方米)
菜园面积:900×2=1800(平方米)
变化六:问题变化
1.求原来图形的面积:①求出原来图形的长和宽(边长);②现在的面积减增加的面积或者现在的面积加减少的面积。
2.求现在图形的面积:①求出现在图形的长和宽(边长);②原来的面积加增加的面积或者原来的面积减减少的面积。
3.求增加或者减少的面积:①求出增加或者减少部分的规则图形的长和宽(边长);②现在的面积与原来的面积相加减
感谢观看
