24.1 第1课时 旋转的概念与性质课件(共22张PPT)
文档属性
| 名称 | 24.1 第1课时 旋转的概念与性质课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
沪科版九年级下册 第二十四章
课程讲授
课程导入
习题解析
课堂总结
24.1 旋 转
第一课时 旋转的概念与性质
前 言
1. 掌握旋转的有关概念及基本性质.(重点)
2. 能够根据旋转的基本性质解决实际问题和进行简单作图.(难点)
学习目标及重难点
在日常生活中,我们可以看到很多旋转的现象,如图:
上图中的各种旋转基本上和我们的生活息息相关,那么对于旋转的世界,我们可以研究点什么呢?这就是本章我们要研究的问题.
课程导入
课程导入
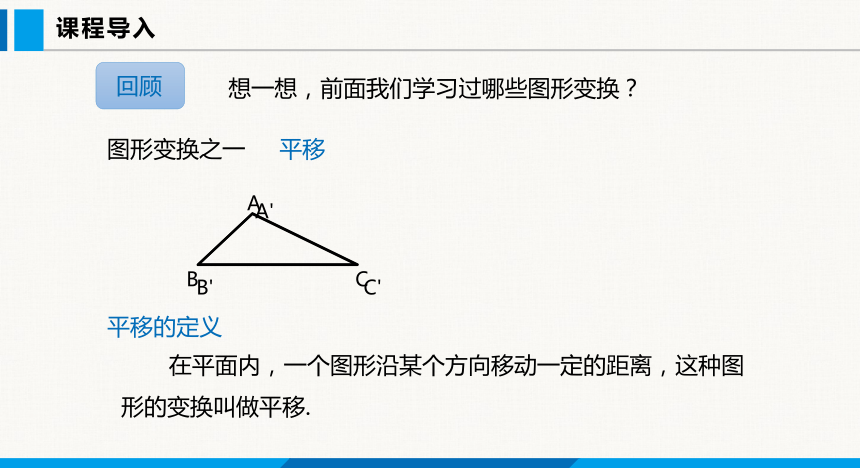
图形变换之一 平移
想一想,前面我们学习过哪些图形变换?
A
B
C
A'
B'
C'
在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
平移的定义
回顾
课程导入
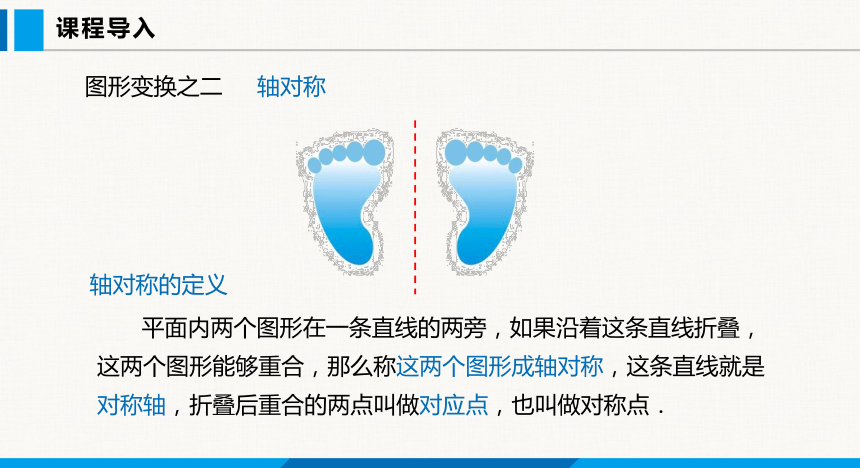
图形变换之二 轴对称
轴对称的定义
平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴,折叠后重合的两点叫做对应点,也叫做对称点.
课程导入
思考:“你能由其中一个花瓣通过平移或轴对称变换得到整个美丽的紫荆花吗?”
不能.
下图是香港特别行政区区旗中央的紫荆花图案.
今天我们来学习 图形变换之三 旋转
看一看:观察下图中图形的运动,试着发现它们的规律.
课程讲授
新课推进
(1) 以上现象有什么共同特点
(2) 钟表的指针、车轮、电扇的风叶在转动过程中,其形状、大小、位置是否发生变化呢?
(物体绕着一个定点运动)
形状、大小不变,位置发生了改变.
课程讲授
新课推进
探索1:旋转的相关概念
在平面内,一个图形(如△ABC)绕着一个定点(如点O),旋转一定的角度(如θ),得到另一个图形(如△A′B′C′)的变换,叫做旋转.定点O叫做旋转中心,θ叫做旋转角.原图形上一点A旋转后成为点A′,这样的两个点叫做对应点.
旋转的三要素:旋转中心、旋转角、旋转方向.
课程讲授
新课推进
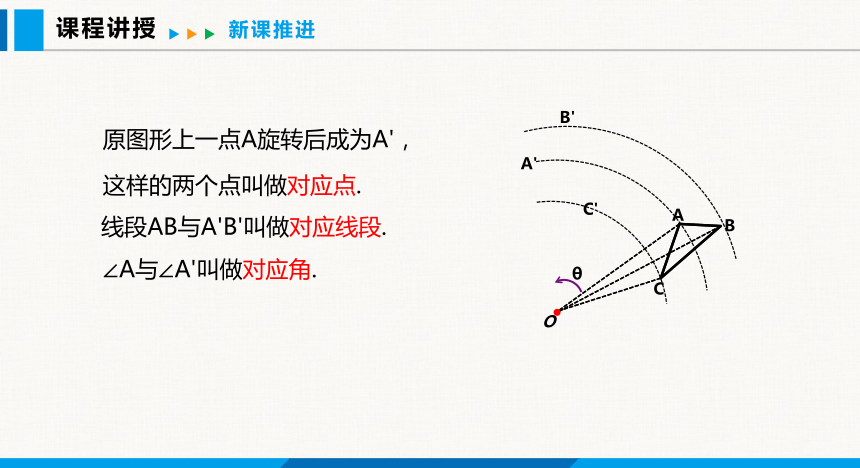
原图形上一点A旋转后成为A',
这样的两个点叫做对应点.
线段AB与A'B'叫做对应线段.
∠A与∠A'叫做对应角.
A
C
B
A
C
B
A
C
B
A
C
B
O
B'
A'
C'
θ
课程讲授
新课推进
如图所示,△ABC是直角三角形,延长AB到D,使
BD=BC,在BC上取BE=AB,连接DE.△ABC旋转后能与△EBD重合,那么:旋转中心是_______;旋转的角度是_______;AC的对应边是______;∠A的对应角是________;点C的对应点是_______.
点B
90°
ED
∠BED
点D
例1
1、下列现象中属于旋转的有 个
①地下水位逐年下降;
②传送带的移动;
③方向盘的转动;
④水龙头开关的转动;
⑤钟摆的运动;
⑥荡秋千运动.
4
√
√
√
√
×
×
课程讲授
新课推进
随堂小练习
课程讲授
新课推进
(3)旋转中心是唯一不动的点.
(3)△ABC ≌△A'B'C'
(2)∠AOA′=∠BOB′=∠COC′.
(1)对应点到旋转中心的距离相等.
(1)OA=OA′,
B
A
B
A
C
C
(2)对应点与旋转中心所连线段的夹角等于旋转角.
OB=OB′,
OC=OC′.
O
探索2:旋转的性质
课程讲授
新课推进
A.30° B.45° C.90° D.135°
1、如图,点A,B,C,D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
C
分析:
对应点与旋转中心的连线的夹角,就是旋转角,由图可知,OB,OD是对应边,∠BOD是旋转角,所以,旋转角为90°.
随堂小练习
课程讲授
新课推进
2、 △A'OB'是△AOB绕点O按逆时针方向旋转得到的. 已知∠AOB=20 °, ∠ A'OB =24°,AB=3,OA=5,则A'B'= ,OA' = ,旋转角等于 .
3
5
44°
课程讲授
新课推进
在平面内,一个图形绕着一个顶点旋转一定的角度θ(0°<θ<360°)后,能够与原图形重合,这样的图形叫做旋转对称图形,这个顶点就是旋转中心.
探索3:旋转对称图形
如图所示的平行四边形ABCD,△COD可以看成是由哪个三角形旋转得到?还能找到几组类似的旋转?
A
B
C
D
O
课程讲授
新课推进
1、如图,要使旋转对称图形通过旋转与自身重合,至少应将它绕旋转中心按逆时针方向旋转( )
A.30° B.60° C.120° D.180°
B
随堂小练习
课程讲授
新课推进
2、下面的图形中既是轴对称图形又是旋转对称图形的是( )
A:是旋转对称图形,但不是轴对称图形
B:是旋转对称图形,也是轴对称图形
D:是旋转对称图形,也是轴对称图形
C:是旋转对称图形,也是轴对称图形
B C D
如图,把△ABC绕点O按顺时针方向旋转60°后得到
△A ′ B ′ C ′ ,则下列等式成立的有( )
①AB=A ′ B ′ ;②OB=OB ′ ;③∠AOA ′ =∠COC ′ ;
④∠COB=∠A ′ OC ′ ;⑤∠AOB=∠BOC ′.
A.2个
B.3个
C.4个
D.5个
B
习题解析
习题1
习题解析
习题2
如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长.
解:∵将△ABC绕点A逆时针旋转得到△ADE,
点C和点E是对应点,
∴ AB=AD=1,∠BAD=∠CAE=90°,
∴ BD=
习题3
习题解析
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,求∠CAB′的度数.
∴∠CAB′=∠C′AB′-∠C′AC=30°.
解: 由旋转的性质可知
AC=AC′,∠C′AB′=∠CAB=70°,
∴∠AC′C=∠ACC′.
∵CC′∥AB,
∴∠ACC′=∠CAB=70°,
∴∠C′AC=40°,
习题解析
K 是正方形 ABCD 内一点,以 AK 为一边作正方形AKLM,使 L、M 在 AK 的同旁,连接 BK 和 DM,试用旋转的思想说明线段BK与DM的数量关系和位置关系.
解:BK=DM,BK ⊥DM.
简要思路:由题意知,△ABK绕点 A逆时针旋转 90°得到△ADM,由旋转性质可知 BK=DM,BK ⊥DM.
A
B
C
D
K
L
M
拓展提升
课程总结
小结
三要素:旋转中心、旋转方向和旋转角度
旋转的概念和性质
性质
①对应点到旋转中心的距离相等;
②两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
③旋转中心是唯一不动的点.
定义
旋转对称图形
沪科版九年级下册 第二十四章
课程讲授
课程导入
习题解析
课堂总结
24.1 旋 转
第一课时 旋转的概念与性质
前 言
1. 掌握旋转的有关概念及基本性质.(重点)
2. 能够根据旋转的基本性质解决实际问题和进行简单作图.(难点)
学习目标及重难点
在日常生活中,我们可以看到很多旋转的现象,如图:
上图中的各种旋转基本上和我们的生活息息相关,那么对于旋转的世界,我们可以研究点什么呢?这就是本章我们要研究的问题.
课程导入
课程导入
图形变换之一 平移
想一想,前面我们学习过哪些图形变换?
A
B
C
A'
B'
C'
在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
平移的定义
回顾
课程导入
图形变换之二 轴对称
轴对称的定义
平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴,折叠后重合的两点叫做对应点,也叫做对称点.
课程导入
思考:“你能由其中一个花瓣通过平移或轴对称变换得到整个美丽的紫荆花吗?”
不能.
下图是香港特别行政区区旗中央的紫荆花图案.
今天我们来学习 图形变换之三 旋转
看一看:观察下图中图形的运动,试着发现它们的规律.
课程讲授
新课推进
(1) 以上现象有什么共同特点
(2) 钟表的指针、车轮、电扇的风叶在转动过程中,其形状、大小、位置是否发生变化呢?
(物体绕着一个定点运动)
形状、大小不变,位置发生了改变.
课程讲授
新课推进
探索1:旋转的相关概念
在平面内,一个图形(如△ABC)绕着一个定点(如点O),旋转一定的角度(如θ),得到另一个图形(如△A′B′C′)的变换,叫做旋转.定点O叫做旋转中心,θ叫做旋转角.原图形上一点A旋转后成为点A′,这样的两个点叫做对应点.
旋转的三要素:旋转中心、旋转角、旋转方向.
课程讲授
新课推进
原图形上一点A旋转后成为A',
这样的两个点叫做对应点.
线段AB与A'B'叫做对应线段.
∠A与∠A'叫做对应角.
A
C
B
A
C
B
A
C
B
A
C
B
O
B'
A'
C'
θ
课程讲授
新课推进
如图所示,△ABC是直角三角形,延长AB到D,使
BD=BC,在BC上取BE=AB,连接DE.△ABC旋转后能与△EBD重合,那么:旋转中心是_______;旋转的角度是_______;AC的对应边是______;∠A的对应角是________;点C的对应点是_______.
点B
90°
ED
∠BED
点D
例1
1、下列现象中属于旋转的有 个
①地下水位逐年下降;
②传送带的移动;
③方向盘的转动;
④水龙头开关的转动;
⑤钟摆的运动;
⑥荡秋千运动.
4
√
√
√
√
×
×
课程讲授
新课推进
随堂小练习
课程讲授
新课推进
(3)旋转中心是唯一不动的点.
(3)△ABC ≌△A'B'C'
(2)∠AOA′=∠BOB′=∠COC′.
(1)对应点到旋转中心的距离相等.
(1)OA=OA′,
B
A
B
A
C
C
(2)对应点与旋转中心所连线段的夹角等于旋转角.
OB=OB′,
OC=OC′.
O
探索2:旋转的性质
课程讲授
新课推进
A.30° B.45° C.90° D.135°
1、如图,点A,B,C,D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
C
分析:
对应点与旋转中心的连线的夹角,就是旋转角,由图可知,OB,OD是对应边,∠BOD是旋转角,所以,旋转角为90°.
随堂小练习
课程讲授
新课推进
2、 △A'OB'是△AOB绕点O按逆时针方向旋转得到的. 已知∠AOB=20 °, ∠ A'OB =24°,AB=3,OA=5,则A'B'= ,OA' = ,旋转角等于 .
3
5
44°
课程讲授
新课推进
在平面内,一个图形绕着一个顶点旋转一定的角度θ(0°<θ<360°)后,能够与原图形重合,这样的图形叫做旋转对称图形,这个顶点就是旋转中心.
探索3:旋转对称图形
如图所示的平行四边形ABCD,△COD可以看成是由哪个三角形旋转得到?还能找到几组类似的旋转?
A
B
C
D
O
课程讲授
新课推进
1、如图,要使旋转对称图形通过旋转与自身重合,至少应将它绕旋转中心按逆时针方向旋转( )
A.30° B.60° C.120° D.180°
B
随堂小练习
课程讲授
新课推进
2、下面的图形中既是轴对称图形又是旋转对称图形的是( )
A:是旋转对称图形,但不是轴对称图形
B:是旋转对称图形,也是轴对称图形
D:是旋转对称图形,也是轴对称图形
C:是旋转对称图形,也是轴对称图形
B C D
如图,把△ABC绕点O按顺时针方向旋转60°后得到
△A ′ B ′ C ′ ,则下列等式成立的有( )
①AB=A ′ B ′ ;②OB=OB ′ ;③∠AOA ′ =∠COC ′ ;
④∠COB=∠A ′ OC ′ ;⑤∠AOB=∠BOC ′.
A.2个
B.3个
C.4个
D.5个
B
习题解析
习题1
习题解析
习题2
如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长.
解:∵将△ABC绕点A逆时针旋转得到△ADE,
点C和点E是对应点,
∴ AB=AD=1,∠BAD=∠CAE=90°,
∴ BD=
习题3
习题解析
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,求∠CAB′的度数.
∴∠CAB′=∠C′AB′-∠C′AC=30°.
解: 由旋转的性质可知
AC=AC′,∠C′AB′=∠CAB=70°,
∴∠AC′C=∠ACC′.
∵CC′∥AB,
∴∠ACC′=∠CAB=70°,
∴∠C′AC=40°,
习题解析
K 是正方形 ABCD 内一点,以 AK 为一边作正方形AKLM,使 L、M 在 AK 的同旁,连接 BK 和 DM,试用旋转的思想说明线段BK与DM的数量关系和位置关系.
解:BK=DM,BK ⊥DM.
简要思路:由题意知,△ABK绕点 A逆时针旋转 90°得到△ADM,由旋转性质可知 BK=DM,BK ⊥DM.
A
B
C
D
K
L
M
拓展提升
课程总结
小结
三要素:旋转中心、旋转方向和旋转角度
旋转的概念和性质
性质
①对应点到旋转中心的距离相等;
②两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
③旋转中心是唯一不动的点.
定义
旋转对称图形
