24.2 第1课时 圆的有关概念、点与圆的位置关系课件(共28张PPT)
文档属性
| 名称 | 24.2 第1课时 圆的有关概念、点与圆的位置关系课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 12:51:23 | ||
图片预览






文档简介
(共28张PPT)
沪科版九年级下册 第二十四章
课程讲授
课程导入
习题解析
课堂总结
24.2 圆的基本性质
第一课时 圆的有关概念、点与圆的位置关系
前 言
1.理解圆的概念及点和圆的三种位置关系,并会利用点到圆心的距离和半径之间的数量关系判定点和圆的位置关系;
2.通过圆的概念及点与圆的位置关系的探究,感受数学知识的内在联系,进一步体会分类讨论和数形结合的思想方法.
学习目标及重难点
课程导入
观察下列生活中的图片,找一找你所熟悉的图形.
课程导入
古希腊的数学家认为,一切立体图形中最美的是球形;一切平面图形中最美的是圆形,它的完美来自于中心对称,无论从哪个位置都具有同一形状,它最协调,最匀称,例如车轮设计成了圆形.
课程导入
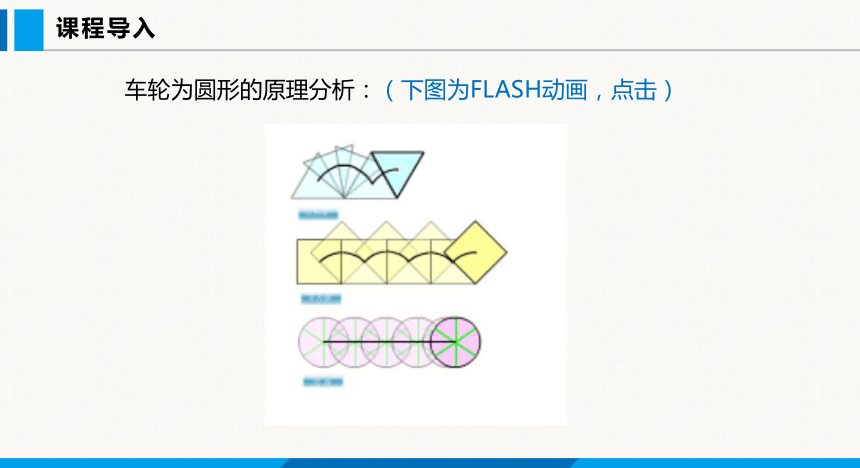
思考:从原理上看车轮为什么做成圆形 做成三角形、正方形可以吗?
课程导入
车轮为圆形的原理分析:(下图为FLASH动画,点击)
课程讲授
新课推进
探索1:探究圆的概念
·
r
O
P
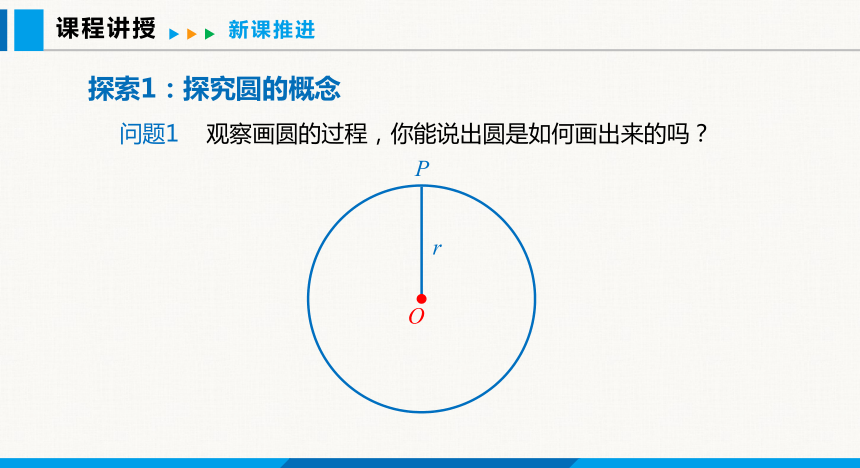
问题1 观察画圆的过程,你能说出圆是如何画出来的吗?
课程讲授
新课推进
(1)动态定义:在平面内,线段 OP 绕着它固定的一个端点 O 旋转一周,另一个端点 P 所形成的封闭曲线叫做圆.固定的端点 O 叫做圆心,线段 OP 的长 r 叫做半径.以点O为圆心的圆,记作“⊙O ” 读作“圆O”.
(2)集合定义:圆也可以看成是所有到定点(圆心)的距离等于定长(半径)的点的集合.
O
·
A
C
E
r
r
r
r
r
D
B
课程讲授
新课推进
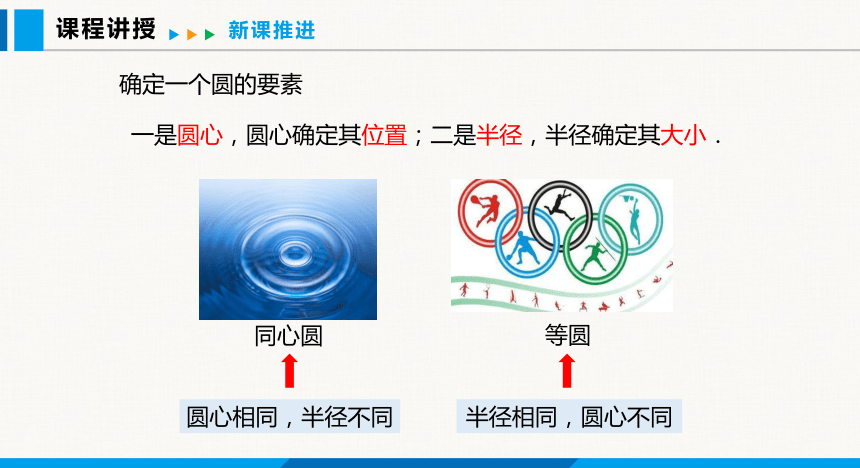
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
已知:如图AB,CD为⊙O 的直径. 求证:AD∥CB.
证明:连接AC,DB.
∵ AB,CD为⊙O的直径,
∴ OA = OB,
OC = OD.
∴ 四边形ADBC为平行四边形,
∴ AD∥CB.
A
B
C
D
O
课程讲授
新课推进
例1
课程讲授
新课推进
下列说法中,错误的有( )
(1)经过点P的圆有无数个;
(2)以点P为圆心的圆有无数个;
(3)半径为3 cm且经过点P的圆有无数个;
(4)以点P为圆心,3 cm为半径的圆有无数个.
A.1个 B.2个 C.3个 D.4个
A
随堂小练习
课程讲授
新课推进
在同一个平面内,点与圆有三种位置关系:
点在圆外、点在圆上和点在圆内.
点P与☉O的位置关系如图所示.
探索2:点和圆的位置关系
P
P
P
点P在⊙O内
点P在⊙O上
点P在⊙O外
课程讲授
新课推进
r
P
O
P
r
O
P
r
O
点P在⊙O外 OP>r;
点P在⊙O上 OP=r;
点P在⊙O内 OP数形结合:
位置关系
数量关系
符号“ ”读作“等价于”,
它表示从符号“ ”的左
端可以推出右端,从右
端也可以推出左端.
如图,已知矩形 ABCD 的边 AB=3,AD=4.
(1)以 A 为圆心,4 为半径作⊙A,则点 B、C、D 与
⊙A的位置关系如何?
解:∵AB = 3cm<4cm,
∴ 点 B 在⊙A 内.
∵ AD = 4cm,
∴ 点 D 在 ⊙A 上.
∵ >4cm,
∴ 点 C 在 ⊙A 外.
课程讲授
新课推进
例2
课程讲授
新课推进
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一 点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围.
解:由题意得,点B一定在圆内,点C一定在圆外,∴3cm<r<5cm.
课程讲授
新课推进
弧:
圆上任意两点间的部分叫做圆弧,简称弧,用符号“ ”表示. 如图,以 A,B 为端点的弧记作 AB ,读作“弧AB”.
(
(
探索3:圆的相关概念
·
C
O
A
B
弦:
连接圆上任意两点的线段(如图中的AB,AC)叫做弦.
经过圆心的弦(如图中的AB)叫
做直径.
·
C
O
A
B
注意:1. 弦和直径都是线段.
2. 直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
课程讲授
新课推进
课程讲授
新课推进
半圆、优弧及劣弧:
圆的任意一条直径的两个端点分圆
成两条弧,每一条弧都叫做半圆.
劣弧与优弧
半圆
大于半圆的弧(如图中的ABC,一般用三个字母表示)叫做优弧;小于半圆的弧(如图中的AC)叫做劣弧.
(
(
·
C
O
A
B
半圆是弧,弧不一定是半圆
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
只有同圆或等圆中才可能有等弧,等弧长度一定相等,但长度相等的弧不一定是等弧
课程讲授
新课推进
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,
记作
劣弧AC,记作
O′
半径OO′
课程讲授
新课推进
课程讲授
新课推进
随堂小练习
1. 下列关于圆的叙述中正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.平面上到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
B
2. 以下命题:①半圆是弧,但弧不一定是半圆;
②过圆上任意一点只能作一条弦,且这条弦是直径;
③弦是直径;④直径是圆中最长的弦;⑤直径不是弦;⑥优弧大于劣弧; ⑦以O为圆心可以画无数个圆.
正确的个数为( )
A.1 B.2 C.3 D.4
C
课程讲授
新课推进
习题解析
习题1
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CP,CM分别是AB边上的高和中线,如果⊙A是以点A为圆心,半径为2的圆,那么下列判断正确的是( )
A.点P,M均在⊙A内
B.点P,M均在⊙A外
C.点P在⊙A内,点M在⊙A外
D.点P在⊙A外,点M在⊙A内
C
习题解析
习题2
1. 如图所示,AB是圆的直径,则图中的弦有 条,分别
是 ,劣弧有 条,分别是 .
2
弦CD,弦AB
5
(
(
(
(
(
AC,CD,DB,AD,BC
2.已知☉O的半径为3,点A在☉O外,OA的取值范围是 ;
点B在☉O上,OB= ;点C(不与点O重合)在☉O内,则OC的取值范围是 .
OA>3
3
0习题3
习题解析
如图,OA、OB是⊙O的半径,点C、D分别为OA、OB的中点,求证:AD=BC.
证明:∵OA、OB是⊙O的半径,∴OA=OB.
∵点C、D分别为OA、OB的中点,
∴OC= OA,OD= OB,
∴OC=OD.又∵∠O=∠O,
∴△AOD≌△BOC(SAS).
∴BC=AD.
习题解析
在Rt△ABC中,∠A=30°,∠C=90°,BC=2,以点A为圆心 r为半径画圆,使点C在⊙A内而点B在⊙A外,则r的取值范围为___ ___.
解析:利用锐角三角函数与勾股定理,求得AB=4,AC= ,则r的取值范围为AC<r<AB,即 .
习题4
习题解析
如图,点O处有一灯塔,警示⊙O内部为危险区,一渔船误入危险区点P处,该渔船应该按什么方向航行 才能尽快离开危险区?试说明理由.
A
D
P
解:渔船应沿着灯塔O过点P的射线OP方向航行才能尽快离开危险区.理由如下:设射线OP交⊙O于点A,过点P任意作一条弦CD,连接OD,在△ODP中,OD-OP<PD,又∵OD=OA,∴OA-OP<PD,∴PA<PD,即渔船沿射线OP方向航行才能尽快离开危险区.
C
O
拓展提升
课程总结
小结
旋转:要画一个确定的圆,关键是确定圆心和半径
圆
有关概念
弦(直径)
定义
集合:同圆半径相等
弧
直径是圆中最长的弦
劣弧
半圆
优弧
半圆是特殊的弧
同圆
等圆
同心圆
沪科版九年级下册 第二十四章
课程讲授
课程导入
习题解析
课堂总结
24.2 圆的基本性质
第一课时 圆的有关概念、点与圆的位置关系
前 言
1.理解圆的概念及点和圆的三种位置关系,并会利用点到圆心的距离和半径之间的数量关系判定点和圆的位置关系;
2.通过圆的概念及点与圆的位置关系的探究,感受数学知识的内在联系,进一步体会分类讨论和数形结合的思想方法.
学习目标及重难点
课程导入
观察下列生活中的图片,找一找你所熟悉的图形.
课程导入
古希腊的数学家认为,一切立体图形中最美的是球形;一切平面图形中最美的是圆形,它的完美来自于中心对称,无论从哪个位置都具有同一形状,它最协调,最匀称,例如车轮设计成了圆形.
课程导入
思考:从原理上看车轮为什么做成圆形 做成三角形、正方形可以吗?
课程导入
车轮为圆形的原理分析:(下图为FLASH动画,点击)
课程讲授
新课推进
探索1:探究圆的概念
·
r
O
P
问题1 观察画圆的过程,你能说出圆是如何画出来的吗?
课程讲授
新课推进
(1)动态定义:在平面内,线段 OP 绕着它固定的一个端点 O 旋转一周,另一个端点 P 所形成的封闭曲线叫做圆.固定的端点 O 叫做圆心,线段 OP 的长 r 叫做半径.以点O为圆心的圆,记作“⊙O ” 读作“圆O”.
(2)集合定义:圆也可以看成是所有到定点(圆心)的距离等于定长(半径)的点的集合.
O
·
A
C
E
r
r
r
r
r
D
B
课程讲授
新课推进
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
已知:如图AB,CD为⊙O 的直径. 求证:AD∥CB.
证明:连接AC,DB.
∵ AB,CD为⊙O的直径,
∴ OA = OB,
OC = OD.
∴ 四边形ADBC为平行四边形,
∴ AD∥CB.
A
B
C
D
O
课程讲授
新课推进
例1
课程讲授
新课推进
下列说法中,错误的有( )
(1)经过点P的圆有无数个;
(2)以点P为圆心的圆有无数个;
(3)半径为3 cm且经过点P的圆有无数个;
(4)以点P为圆心,3 cm为半径的圆有无数个.
A.1个 B.2个 C.3个 D.4个
A
随堂小练习
课程讲授
新课推进
在同一个平面内,点与圆有三种位置关系:
点在圆外、点在圆上和点在圆内.
点P与☉O的位置关系如图所示.
探索2:点和圆的位置关系
P
P
P
点P在⊙O内
点P在⊙O上
点P在⊙O外
课程讲授
新课推进
r
P
O
P
r
O
P
r
O
点P在⊙O外 OP>r;
点P在⊙O上 OP=r;
点P在⊙O内 OP
位置关系
数量关系
符号“ ”读作“等价于”,
它表示从符号“ ”的左
端可以推出右端,从右
端也可以推出左端.
如图,已知矩形 ABCD 的边 AB=3,AD=4.
(1)以 A 为圆心,4 为半径作⊙A,则点 B、C、D 与
⊙A的位置关系如何?
解:∵AB = 3cm<4cm,
∴ 点 B 在⊙A 内.
∵ AD = 4cm,
∴ 点 D 在 ⊙A 上.
∵ >4cm,
∴ 点 C 在 ⊙A 外.
课程讲授
新课推进
例2
课程讲授
新课推进
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一 点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围.
解:由题意得,点B一定在圆内,点C一定在圆外,∴3cm<r<5cm.
课程讲授
新课推进
弧:
圆上任意两点间的部分叫做圆弧,简称弧,用符号“ ”表示. 如图,以 A,B 为端点的弧记作 AB ,读作“弧AB”.
(
(
探索3:圆的相关概念
·
C
O
A
B
弦:
连接圆上任意两点的线段(如图中的AB,AC)叫做弦.
经过圆心的弦(如图中的AB)叫
做直径.
·
C
O
A
B
注意:1. 弦和直径都是线段.
2. 直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
课程讲授
新课推进
课程讲授
新课推进
半圆、优弧及劣弧:
圆的任意一条直径的两个端点分圆
成两条弧,每一条弧都叫做半圆.
劣弧与优弧
半圆
大于半圆的弧(如图中的ABC,一般用三个字母表示)叫做优弧;小于半圆的弧(如图中的AC)叫做劣弧.
(
(
·
C
O
A
B
半圆是弧,弧不一定是半圆
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
只有同圆或等圆中才可能有等弧,等弧长度一定相等,但长度相等的弧不一定是等弧
课程讲授
新课推进
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,
记作
劣弧AC,记作
O′
半径OO′
课程讲授
新课推进
课程讲授
新课推进
随堂小练习
1. 下列关于圆的叙述中正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.平面上到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
B
2. 以下命题:①半圆是弧,但弧不一定是半圆;
②过圆上任意一点只能作一条弦,且这条弦是直径;
③弦是直径;④直径是圆中最长的弦;⑤直径不是弦;⑥优弧大于劣弧; ⑦以O为圆心可以画无数个圆.
正确的个数为( )
A.1 B.2 C.3 D.4
C
课程讲授
新课推进
习题解析
习题1
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CP,CM分别是AB边上的高和中线,如果⊙A是以点A为圆心,半径为2的圆,那么下列判断正确的是( )
A.点P,M均在⊙A内
B.点P,M均在⊙A外
C.点P在⊙A内,点M在⊙A外
D.点P在⊙A外,点M在⊙A内
C
习题解析
习题2
1. 如图所示,AB是圆的直径,则图中的弦有 条,分别
是 ,劣弧有 条,分别是 .
2
弦CD,弦AB
5
(
(
(
(
(
AC,CD,DB,AD,BC
2.已知☉O的半径为3,点A在☉O外,OA的取值范围是 ;
点B在☉O上,OB= ;点C(不与点O重合)在☉O内,则OC的取值范围是 .
OA>3
3
0
习题解析
如图,OA、OB是⊙O的半径,点C、D分别为OA、OB的中点,求证:AD=BC.
证明:∵OA、OB是⊙O的半径,∴OA=OB.
∵点C、D分别为OA、OB的中点,
∴OC= OA,OD= OB,
∴OC=OD.又∵∠O=∠O,
∴△AOD≌△BOC(SAS).
∴BC=AD.
习题解析
在Rt△ABC中,∠A=30°,∠C=90°,BC=2,以点A为圆心 r为半径画圆,使点C在⊙A内而点B在⊙A外,则r的取值范围为___ ___.
解析:利用锐角三角函数与勾股定理,求得AB=4,AC= ,则r的取值范围为AC<r<AB,即 .
习题4
习题解析
如图,点O处有一灯塔,警示⊙O内部为危险区,一渔船误入危险区点P处,该渔船应该按什么方向航行 才能尽快离开危险区?试说明理由.
A
D
P
解:渔船应沿着灯塔O过点P的射线OP方向航行才能尽快离开危险区.理由如下:设射线OP交⊙O于点A,过点P任意作一条弦CD,连接OD,在△ODP中,OD-OP<PD,又∵OD=OA,∴OA-OP<PD,∴PA<PD,即渔船沿射线OP方向航行才能尽快离开危险区.
C
O
拓展提升
课程总结
小结
旋转:要画一个确定的圆,关键是确定圆心和半径
圆
有关概念
弦(直径)
定义
集合:同圆半径相等
弧
直径是圆中最长的弦
劣弧
半圆
优弧
半圆是特殊的弧
同圆
等圆
同心圆
