24.2 第3课时 圆心角、弧、弦、弦心距间关系课件(共22张PPT)
文档属性
| 名称 | 24.2 第3课时 圆心角、弧、弦、弦心距间关系课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
沪科版九年级下册 第二十四章
课程讲授
课程导入
习题解析
课堂总结
24.2 圆的基本性质
第三课时 圆心角、弧、弦、弦心距间关系
前 言
1. 结合图形了解圆心角的概念,掌握圆心角的相关性质.
2. 能够发现圆心角、弧、弦、弦心距间关系,并会初步运用这些关系解决有关问题 (重点、难点).
学习目标及重难点
课程导入
飞镖靶、闹钟以及被均分的蛋糕等圆形中,都存在着角,那么这些角有什么共同的特征呢?
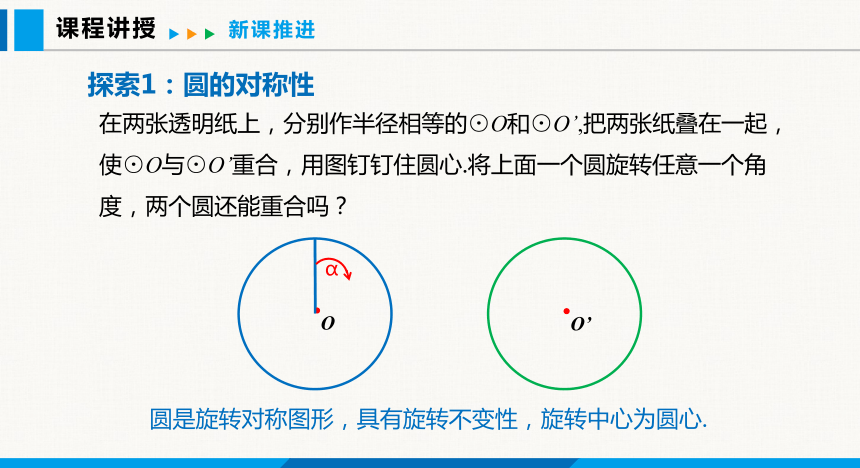
在两张透明纸上,分别作半径相等的⊙O和⊙O’,把两张纸叠在一起,使⊙O与⊙O’重合,用图钉钉住圆心.将上面一个圆旋转任意一个角度,两个圆还能重合吗?
O’
O
α
圆是旋转对称图形,具有旋转不变性,旋转中心为圆心.
课程讲授
新课推进
探索1:圆的对称性
课程讲授
新课推进
探索2:圆心角
O
A
B
M
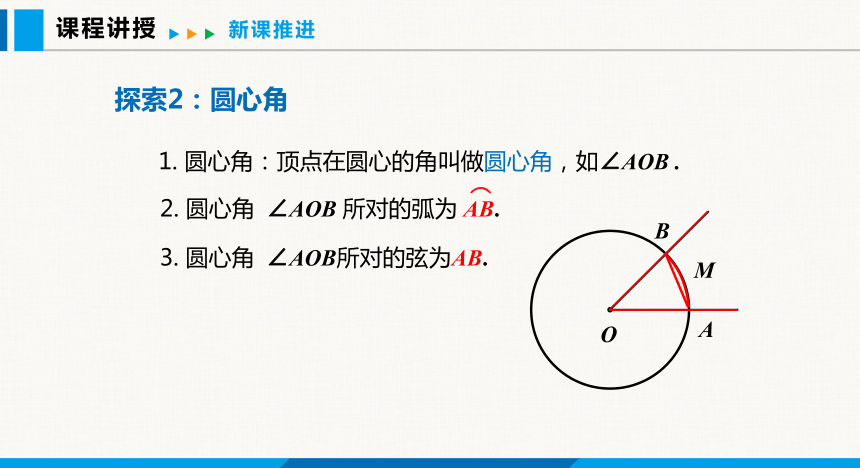
1. 圆心角:顶点在圆心的角叫做圆心角,如∠AOB .
3. 圆心角 ∠AOB所对的弦为AB.
2. 圆心角 ∠AOB 所对的弧为 AB.
⌒
课程讲授
新课推进
例1
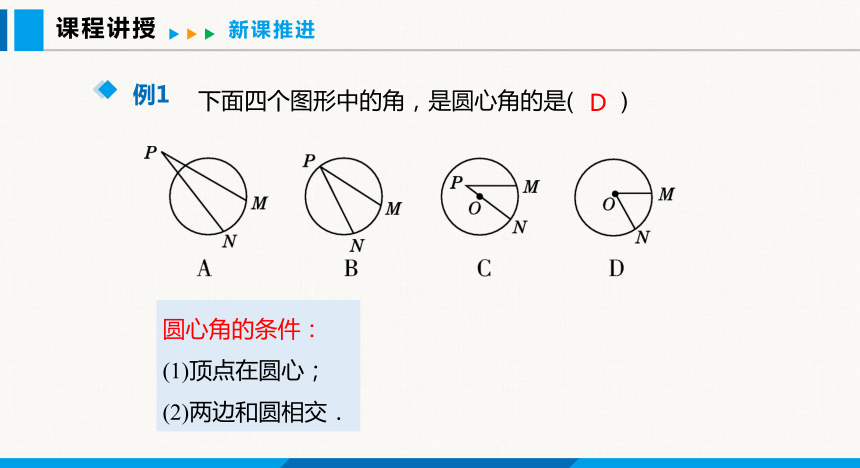
下面四个图形中的角,是圆心角的是( )
D
圆心角的条件:
(1)顶点在圆心;
(2)两边和圆相交.
课程讲授
新课推进
1.在同圆中探究
在☉O中,如果∠AOB= ∠COD,那么AB与CD,弦AB与弦CD,弦心距OE与OF有怎样的数量关系?
⌒
⌒
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么,AB=CD,弦AB=弦CD,OE=OF
⌒
⌒
·
O
A
B
C
D
E
F
探索3:圆心角、弧、弦、弦心距间的关系
课程讲授
新课推进
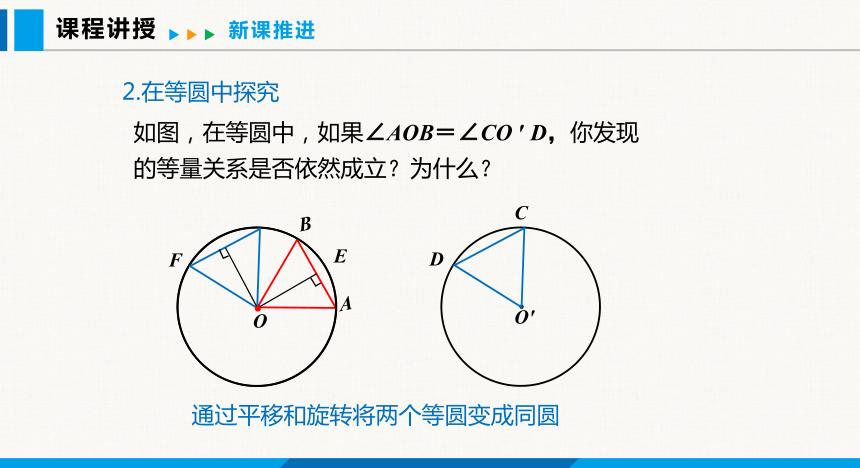
2.在等圆中探究
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关系是否依然成立?为什么?
O
C
·
O'
D
通过平移和旋转将两个等圆变成同圆
·
A
B
┐
E
F
·
┐
课程讲授
新课推进
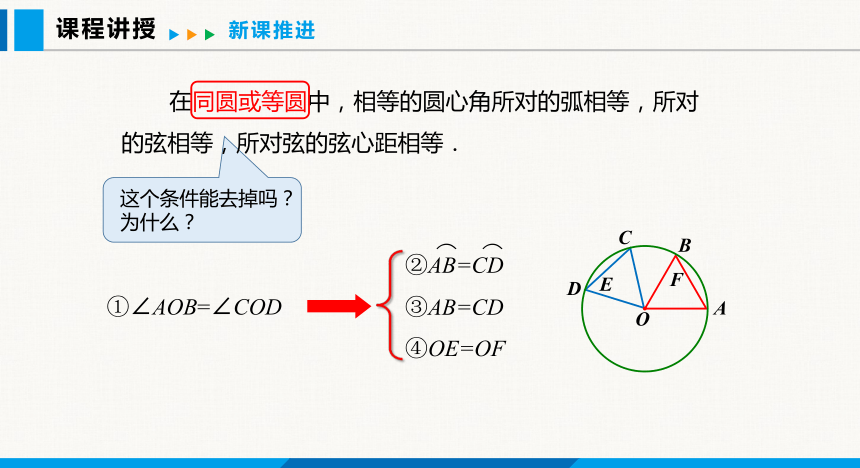
这个条件能去掉吗?为什么?
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
A
B
O
D
C
E
F
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
④OE=OF
课程讲授
新课推进
在同圆或等圆中,如果两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距中,有一组量相等,那么其余各组量都分别相等.
圆心角相等
弧相等
弦相等
弦心距相等
课程讲授
新课推进
已知:如图,等边三角形ABC的三个顶点都在⊙O上.
求证: ∠ AOB= ∠ BOC = ∠ COA =120°.
A
B
C
O
证明:连接OA,OB,OC,如图.
∵ AB=BC=CA,
∴∠AOB =∠BOC =∠COA
弦相等
圆心角相等
例2
课程讲授
新课推进
已知:如图,点O是∠A平分线上的一点,
⊙O分别交∠A两边于点C,D和点 E,F.
求证:CD=EF.
证明:过点O作OK ⊥ CD、OK ′ ⊥EF,
垂足分别为K,K ′ .
O
A
D
E
F
C
K ′
K
∴ OK = OK ′ (角平分线性质),
∴ CD =EF.
弦心距相等
弦相等
例3
课程讲授
新课推进
解:连接OE,如图.
∴ ∠COE=40°,
∵CE∥AB,
∴∠BOD=∠C=70°.
∵ CE为40°,
⌒
⌒
如图,AB,CD为⊙O的两条直径,CE为⊙O的弦,且CE // AB,CE为40°,求∠ BOD的度数.
O
C
E
A
B
D
例4
课程讲授
新课推进
1. 如果两个圆心角相等,那么( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
D
随堂小练习
课程讲授
新课推进
2. 在同圆中,圆心角∠AOB=2∠COD,则 AB 与CD
的关系是( )
⌒ ⌒
A. AB=2CD
⌒ ⌒
B. AB >CD
⌒ ⌒
C. AB⌒ ⌒
D. 不能确定
A
习题解析
习题1
如图,已知 AB、CD 为 ☉O 的两条弦, .
求证:AB=CD.
C
A
B
D
O
证明:连接AO,BO,CO,DO.
即
∵ AD=BC,
⌒
⌒
习题解析
习题2
如图,AB是☉O的直径,点C在☉上,∠AOC=40°,D是BC的中点,求∠OCD的度数.
⌒
解:连接OD.
∵ AB是☉O的直径,∠AOC=40°,
∴ ∠BOC=140°.
∵ D是BC的中点,
∴ ∠COD=∠BOD= ∠BOC=70°,
∵ OC=OD,
∴ ∠OCD=∠ODC= (180°-∠COD)=55°
⌒
习题3
习题解析
如图,在⊙O中,AD,BC相交于点E,OE平分∠AEC.
(1)求证:AB=CD;
(2)如果⊙O的半径为5,AD⊥CB,DE=1,求AD的长.
习题解析
解:(1)证明:
过点O作OM⊥AD,ON⊥BC,垂足分别为M,N,
∵ OE平分∠AEC,
∴ OM=ON,
∴ AD=BC ,
∴ AD-BD =BC -BD ,
即 AB=CD ,
∴ AB=CD
︵
︵
︵
︵
︵
︵
︵
︵
习题解析
(2)连接OD
∵ OM⊥AD,∴ AM=DM
∵AD⊥CB,OE平分∠AEC
∴∠OEM=45°,∴∠EOM=45°
∴∠OEM=∠EOM,∴OM=ME=DM-1
在 Rt△DOM 中,OD2=OM 2+DM 2,
即 25=(DM-1)2+DM 2,
解得 DM=4 或 DM=-3(舍去).
∴ AD=2DM=8,即AD的长为8.
习题解析
拓展提升
如图,在☉O中,2∠AOB =∠COD,那么CD = 2AB
成立吗?CD = 2AB呢?如果成立,请说明理由;如
不成立,那它们之间的关系又是什么?
⌒ ⌒
A
B
C
D
E
O
解:CD =2AB 成立,CD =2AB 不成立.理由如下:
取 CD 的中点 E,连接 OE,CE,DE ,
那么∠AOB=∠COE =∠DOE,
所以 AB = CE = DE ,CD =2 AB ,
弦AB = CE = DE,
在△CDE中,CE+DE > CD,即 CD < 2AB.
⌒ ⌒
⌒
⌒
⌒
⌒
⌒
⌒
课程总结
小结
顶点在圆心的角,叫圆心角.
圆心角、弧、弦、弦心距
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
圆心角
在同圆或等圆中,如果两条弧相等,那么它们所对应的圆心角相等,所对的弦相等.
在同圆或等圆中,如果两条弦相等,那么它们所对应的圆心角相等,所对的优弧和劣弧分别相等.
圆心角、弧、弦、弦心距间关系
沪科版九年级下册 第二十四章
课程讲授
课程导入
习题解析
课堂总结
24.2 圆的基本性质
第三课时 圆心角、弧、弦、弦心距间关系
前 言
1. 结合图形了解圆心角的概念,掌握圆心角的相关性质.
2. 能够发现圆心角、弧、弦、弦心距间关系,并会初步运用这些关系解决有关问题 (重点、难点).
学习目标及重难点
课程导入
飞镖靶、闹钟以及被均分的蛋糕等圆形中,都存在着角,那么这些角有什么共同的特征呢?
在两张透明纸上,分别作半径相等的⊙O和⊙O’,把两张纸叠在一起,使⊙O与⊙O’重合,用图钉钉住圆心.将上面一个圆旋转任意一个角度,两个圆还能重合吗?
O’
O
α
圆是旋转对称图形,具有旋转不变性,旋转中心为圆心.
课程讲授
新课推进
探索1:圆的对称性
课程讲授
新课推进
探索2:圆心角
O
A
B
M
1. 圆心角:顶点在圆心的角叫做圆心角,如∠AOB .
3. 圆心角 ∠AOB所对的弦为AB.
2. 圆心角 ∠AOB 所对的弧为 AB.
⌒
课程讲授
新课推进
例1
下面四个图形中的角,是圆心角的是( )
D
圆心角的条件:
(1)顶点在圆心;
(2)两边和圆相交.
课程讲授
新课推进
1.在同圆中探究
在☉O中,如果∠AOB= ∠COD,那么AB与CD,弦AB与弦CD,弦心距OE与OF有怎样的数量关系?
⌒
⌒
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么,AB=CD,弦AB=弦CD,OE=OF
⌒
⌒
·
O
A
B
C
D
E
F
探索3:圆心角、弧、弦、弦心距间的关系
课程讲授
新课推进
2.在等圆中探究
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关系是否依然成立?为什么?
O
C
·
O'
D
通过平移和旋转将两个等圆变成同圆
·
A
B
┐
E
F
·
┐
课程讲授
新课推进
这个条件能去掉吗?为什么?
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
A
B
O
D
C
E
F
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
④OE=OF
课程讲授
新课推进
在同圆或等圆中,如果两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距中,有一组量相等,那么其余各组量都分别相等.
圆心角相等
弧相等
弦相等
弦心距相等
课程讲授
新课推进
已知:如图,等边三角形ABC的三个顶点都在⊙O上.
求证: ∠ AOB= ∠ BOC = ∠ COA =120°.
A
B
C
O
证明:连接OA,OB,OC,如图.
∵ AB=BC=CA,
∴∠AOB =∠BOC =∠COA
弦相等
圆心角相等
例2
课程讲授
新课推进
已知:如图,点O是∠A平分线上的一点,
⊙O分别交∠A两边于点C,D和点 E,F.
求证:CD=EF.
证明:过点O作OK ⊥ CD、OK ′ ⊥EF,
垂足分别为K,K ′ .
O
A
D
E
F
C
K ′
K
∴ OK = OK ′ (角平分线性质),
∴ CD =EF.
弦心距相等
弦相等
例3
课程讲授
新课推进
解:连接OE,如图.
∴ ∠COE=40°,
∵CE∥AB,
∴∠BOD=∠C=70°.
∵ CE为40°,
⌒
⌒
如图,AB,CD为⊙O的两条直径,CE为⊙O的弦,且CE // AB,CE为40°,求∠ BOD的度数.
O
C
E
A
B
D
例4
课程讲授
新课推进
1. 如果两个圆心角相等,那么( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
D
随堂小练习
课程讲授
新课推进
2. 在同圆中,圆心角∠AOB=2∠COD,则 AB 与CD
的关系是( )
⌒ ⌒
A. AB=2CD
⌒ ⌒
B. AB >CD
⌒ ⌒
C. AB
D. 不能确定
A
习题解析
习题1
如图,已知 AB、CD 为 ☉O 的两条弦, .
求证:AB=CD.
C
A
B
D
O
证明:连接AO,BO,CO,DO.
即
∵ AD=BC,
⌒
⌒
习题解析
习题2
如图,AB是☉O的直径,点C在☉上,∠AOC=40°,D是BC的中点,求∠OCD的度数.
⌒
解:连接OD.
∵ AB是☉O的直径,∠AOC=40°,
∴ ∠BOC=140°.
∵ D是BC的中点,
∴ ∠COD=∠BOD= ∠BOC=70°,
∵ OC=OD,
∴ ∠OCD=∠ODC= (180°-∠COD)=55°
⌒
习题3
习题解析
如图,在⊙O中,AD,BC相交于点E,OE平分∠AEC.
(1)求证:AB=CD;
(2)如果⊙O的半径为5,AD⊥CB,DE=1,求AD的长.
习题解析
解:(1)证明:
过点O作OM⊥AD,ON⊥BC,垂足分别为M,N,
∵ OE平分∠AEC,
∴ OM=ON,
∴ AD=BC ,
∴ AD-BD =BC -BD ,
即 AB=CD ,
∴ AB=CD
︵
︵
︵
︵
︵
︵
︵
︵
习题解析
(2)连接OD
∵ OM⊥AD,∴ AM=DM
∵AD⊥CB,OE平分∠AEC
∴∠OEM=45°,∴∠EOM=45°
∴∠OEM=∠EOM,∴OM=ME=DM-1
在 Rt△DOM 中,OD2=OM 2+DM 2,
即 25=(DM-1)2+DM 2,
解得 DM=4 或 DM=-3(舍去).
∴ AD=2DM=8,即AD的长为8.
习题解析
拓展提升
如图,在☉O中,2∠AOB =∠COD,那么CD = 2AB
成立吗?CD = 2AB呢?如果成立,请说明理由;如
不成立,那它们之间的关系又是什么?
⌒ ⌒
A
B
C
D
E
O
解:CD =2AB 成立,CD =2AB 不成立.理由如下:
取 CD 的中点 E,连接 OE,CE,DE ,
那么∠AOB=∠COE =∠DOE,
所以 AB = CE = DE ,CD =2 AB ,
弦AB = CE = DE,
在△CDE中,CE+DE > CD,即 CD < 2AB.
⌒ ⌒
⌒
⌒
⌒
⌒
⌒
⌒
课程总结
小结
顶点在圆心的角,叫圆心角.
圆心角、弧、弦、弦心距
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
圆心角
在同圆或等圆中,如果两条弧相等,那么它们所对应的圆心角相等,所对的弦相等.
在同圆或等圆中,如果两条弦相等,那么它们所对应的圆心角相等,所对的优弧和劣弧分别相等.
圆心角、弧、弦、弦心距间关系
