新课标A版选修4-4普通方程与参数方程的转化
文档属性
| 名称 | 新课标A版选修4-4普通方程与参数方程的转化 |

|
|
| 格式 | rar | ||
| 文件大小 | 68.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-25 00:00:00 | ||
图片预览






文档简介
课件18张PPT。4.4.2 参数方程和普通方程的互化
高二(1)班
教师:张青娄思考:1. 思考普通方程与参数方程的异同点。
2.列举我们学习过的曲线的标准方程。
3.曲线的参数方程 表示什么曲线?
参数方程与普通方程: 一般地, 在平面直角坐标系中,如果曲线上任意一点的坐标x, y都是某个变数t的函数
并且对于t的每一个允许值, 由方程组(2) 所确定的点M(x,y)都在这条曲线上, 那么方程(2) 就叫做这条曲线的参数方程, 联系变数x,y的变数t叫做参变数, 简称参数.(2) 相对于参数方程而言,直接给出点的坐标间关系的方程 叫做普通方程。 引例:⑴把参数方程 化为普通方程。1.代入消元法:利用解方程的技巧求出参数t,然后代入消去参数参数方程化为普通方程变式1:把下列参数方程化为普通方程,并说明表示什么曲线?
(1)
(2)
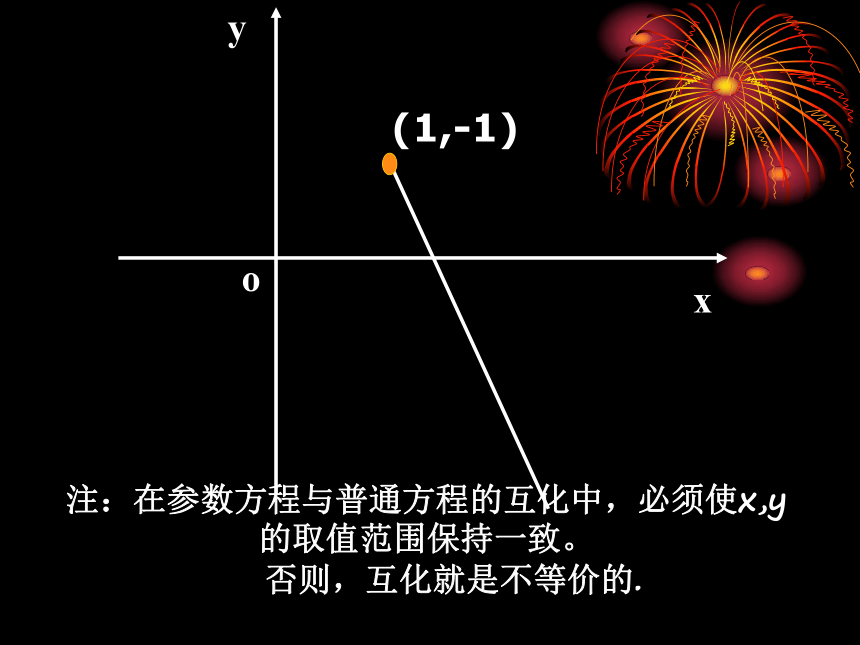
这是以(1,1)为端点的一条射线(包括端点)(1,-1)注:在参数方程与普通方程的互化中,必须使x,y的取值范围保持一致。
否则,互化就是不等价的. 2.三角法:利用三角恒等式消去参数引例:参数方程 ( 为参
数)化为普通方程分析:由 可得变式2:把下列参数方程化为普通方程(1)
(2)变式3.把参数方程化为普通方程,并说明表示什么图形x3.整体消元法:根据参数方程本身的结构特征,从整体上消去。 例:步骤:
1、消掉参数(代入消元,三角变形,配 方消元)
2、写出定义域(x的范围)参数方程化为普通方程的步骤在参数方程与普通方程的互化中,必须使x,y前后的取值范围保持一致。注意:小结: 参数方程化为普通方程的过程就是消参过程常见方法有三种:1.代入法:利用解方程的技巧求出参数t,然后代入消
去参数
2.三角法:利用三角恒等式消去参数
3.整体消元法:根据参数方程本身的结构特征,从
整体上消去。化参数方程为普通方程为F(x,y)=0:在消参过程中注意变量x、y取值范围的一致性,必须根据参数的取值范围,确定f(t)和g(t)值域得x、y的取值范围。普通方程转化为参数方程
教师:张青娄思考:1. 思考普通方程与参数方程的异同点。
2.列举我们学习过的曲线的标准方程。
3.曲线的参数方程 表示什么曲线?
参数方程与普通方程: 一般地, 在平面直角坐标系中,如果曲线上任意一点的坐标x, y都是某个变数t的函数
并且对于t的每一个允许值, 由方程组(2) 所确定的点M(x,y)都在这条曲线上, 那么方程(2) 就叫做这条曲线的参数方程, 联系变数x,y的变数t叫做参变数, 简称参数.(2) 相对于参数方程而言,直接给出点的坐标间关系的方程 叫做普通方程。 引例:⑴把参数方程 化为普通方程。1.代入消元法:利用解方程的技巧求出参数t,然后代入消去参数参数方程化为普通方程变式1:把下列参数方程化为普通方程,并说明表示什么曲线?
(1)
(2)
这是以(1,1)为端点的一条射线(包括端点)(1,-1)注:在参数方程与普通方程的互化中,必须使x,y的取值范围保持一致。
否则,互化就是不等价的. 2.三角法:利用三角恒等式消去参数引例:参数方程 ( 为参
数)化为普通方程分析:由 可得变式2:把下列参数方程化为普通方程(1)
(2)变式3.把参数方程化为普通方程,并说明表示什么图形x3.整体消元法:根据参数方程本身的结构特征,从整体上消去。 例:步骤:
1、消掉参数(代入消元,三角变形,配 方消元)
2、写出定义域(x的范围)参数方程化为普通方程的步骤在参数方程与普通方程的互化中,必须使x,y前后的取值范围保持一致。注意:小结: 参数方程化为普通方程的过程就是消参过程常见方法有三种:1.代入法:利用解方程的技巧求出参数t,然后代入消
去参数
2.三角法:利用三角恒等式消去参数
3.整体消元法:根据参数方程本身的结构特征,从
整体上消去。化参数方程为普通方程为F(x,y)=0:在消参过程中注意变量x、y取值范围的一致性,必须根据参数的取值范围,确定f(t)和g(t)值域得x、y的取值范围。普通方程转化为参数方程
