北师大版七年级数学上册第四章基本平面图形 单元复习题(含解析)
文档属性
| 名称 | 北师大版七年级数学上册第四章基本平面图形 单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 218.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览




文档简介
北师大版七年级数学上册第四章基本平面图形单元复习题
一、单选题
1.如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形的是( )
A. B.
C. D.
2.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是( )
A.以点C为圆心,OD为半径的弧 B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧 D.以点E为圆心,DM为半径的弧
3.如图,点 是 的中点,点 是 的中点,则下列等式中正确的有( )
①②③④
A.4个 B.3个 C.2个 D.1个
4. 把一副三角板按如图所示拼在一起,则等于( )
A. B. C. D.
5.若一个n边形从一个顶点最多能引出5条对角线,则n是( )
A.5 B.8 C.9 D.10
6.下列说法中正确的是( )
A.两个半圆是等弧
B.过圆内一点仅可以作出1条圆的最长弦
C.相等的圆心角所对的弧相等
D.同圆中优弧与半圆的差必是劣弧
7.数轴上表示﹣1的点到表示x的距离为3,则x表示的数为( )
A.2 B.﹣2 C.﹣4 D.2或﹣4
8.如图,O为直线AB上一点,OE、OF分别是∠AOC、∠BOC的平分线,则∠EOF的度数是( )
A.60° B.80° C.90° D.100°
9.如图,已知线段AB=10cm,M是AB中点,点N在AB上,MN=3cm,那么线段NB的长为( )
A.2cm B.3cm C.5cm D.8cm
10.以下说法正确的是( ).
A.直线l上有两个端点 B.经过A,B两点的线段只有一条
C.延长线段AB到C,使AC=BC D.反向延长线段BC至A,使AB=BC
二、填空题
11.时钟在14点30分时,这时刻钟面上时针与分针夹角的度数为 .
12.要把一根木条在墙上钉牢,至少需要 枚钉子.其中的道理是
13.直线l上的线段分别长,M、N分别是的中点,则 .
14.如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 度.
三、解答题
15.已知线段AB,延长AB到C,使BC=AB,再反向延长AB到D,使AD=AB.若CD=26cm,求线段AB的长.
16.已知线段AC和BC在一条直线上,如果AC=5.6cm,BC=2.4cm,E为AC的中点,F为BC的中点,求EF的长.
17.已知一条射线OA,如果从点O再引两条射线OB和OC,使∠AOB=60°,∠BOC=20°,求∠AOC的度数.
18. 如图,已知点C在线段AB上,M,N分别是AC,BC的中点.
(1)若线段AC=12,BC=8,求线段MN的长度.
(2)设AB=a,求线段MN的长度.
(3)解决问题:已知线段DE,延长DE到F,使EF= DE;延长ED到G,使DG=2DE,P,Q分别是EF,DG的中点.若PQ=18 cm,求DE的长.
四、作图题
19.如图,平面上有四个点A,B,C,D.
(1)根据下列语句画图:
①射线BA;
②直线AD,BC相交于点E;
③在线段DC的延长线上取一点F,使CF=BC,连接EF.
(2)图中以E为顶点的角中,小于平角的角共有 个.
20.已知线段AB,反向延长线段AB到C,使 ,D为BC的中点,E为BD的中点.
(1)补全图形;
(2)若 ,求AE的长度.
21.如图所示,已知∠BOC=2∠AOC,OD平分∠AOB,
(1)若∠COD=18°,求∠AOC的度数.
(2)若∠COD=α,试用α表示∠AOC.
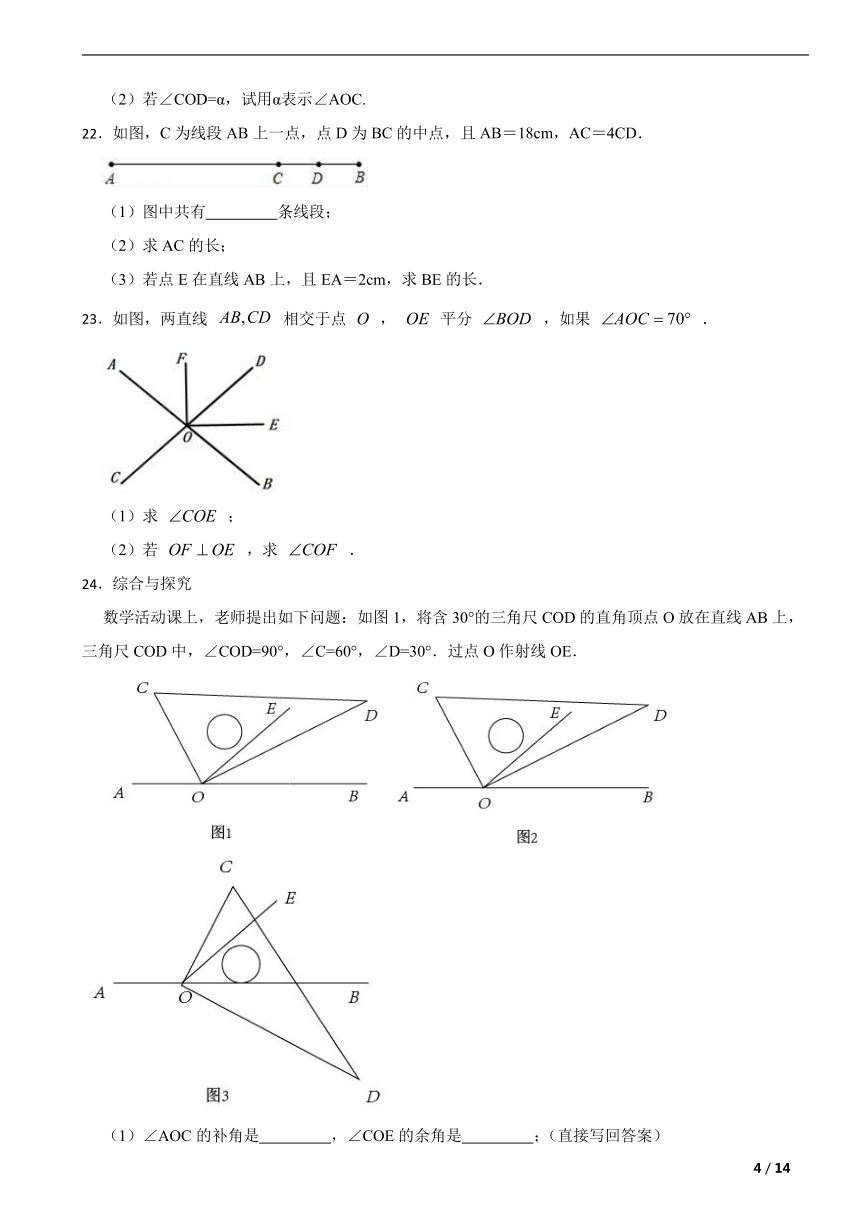
22.如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
23.如图,两直线 相交于点 , 平分 ,如果 .
(1)求 ;
(2)若 ,求 .
24.综合与探究
数学活动课上,老师提出如下问题:如图1,将含30°的三角尺COD的直角顶点O放在直线AB上,三角尺COD中,∠COD=90°,∠C=60°,∠D=30°.过点O作射线OE.
(1)∠AOC的补角是 ,∠COE的余角是 ;(直接写回答案)
(2)如图2,“启航”小组根据学习几何积累的活动经验:特殊的位置可以得到特殊的结论,在图1的基础上继续展开探究,他们提出的问题是:调整三角尺的位置,当OD平分∠BOE时,OC平分∠AOE.请你证明启航小组提出的问题;
(3)如图3,受到“启航”小组的启发,“睿智”小组提出的问题是:在图2的基础上,继续调整三角尺的位置,当OE平分∠BOC时,∠AOC与∠DOE有怎样的数量关系?请说明理由.
答案解析部分
1.【答案】D
【解析】【解答】解:A、以O为顶点的角不止一个,不能用∠O表示,故A选项不符合题意;
B、以O为顶点的角不止一个,不能用∠O表示,故B选项不符合题意;
C、以O为顶点的角不止一个,不能用∠O表示,故C选项不符合题意;
D、能用∠1,∠AOB,∠O三种方法表示同一个角,故D选项符合题意.
故答案为:D.
【分析】根据角的四种表示方法和具体要求回答即可.
2.【答案】D
【解析】【解答】解:根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧
故答案为:D
【分析】根据尺规作图,作一个角等于已知角可知弧FG是以点E为圆心,DM为半径的弧.
3.【答案】C
【解析】【解答】∵点 是 的中点,点 是 的中点,
∴AC=BC,CD=BD,
∵CD=CB-BD=AC-BD,
∴①符合题意,
∵AD-BC=AC+CD-BC=CD,
∴②符合题意,
∵2AD-AB=2AC+2CD-AB=2CD=2BD ,
∴③不符合题意,
∵CD= BC, BC= AB,即CD= AB,
∴④不符合题意,
综上只有两个是正确的,
故答案为:C.
【分析】根据线段的中点,即可找到线段之间的数量关系.
4.【答案】D
【解析】【解答】解:三角板的六个角分别为:90°,45°,45°,90°,60°,30°
如图拼接,可得∠ABC=30°+90°=120°
故答案为:D
【分析】本题考查三角形角度的计算,熟悉三角板的角度是关键。
5.【答案】B
【解析】【解答】解:根据题意可得:n-3=5,
解得:n=8.
故答案为:B.
【分析】从n边形的一个顶点作对角线的条数为(n-3)条,据此求解.
6.【答案】D
【解析】【解答】解:A、在同圆或等圆中,两个半圆是等弧,故原题说法错误;
B、过圆内一点(此点不是圆心)仅可以作出1条圆的最长弦,故原题说法错误;
C、在同圆或等圆中,相等的圆心角所对的弧相等,故原题说法错误;
D、同圆中优弧与半圆的差必是劣弧,说法正确;
故选:D.
【分析】根据圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆,大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧,连接圆上任意两点的线段叫弦的相关定义分别进行分析即可.
7.【答案】D
【解析】【解答】解:由题意得:|x﹣(﹣1)|=3,
∴|x+1|=3,
∴x+1=±3,
∴x=2或﹣4.
故答案为:D.
【分析】数轴上任意两点间的距离等于这两点所表示数差的绝对值,据此列出方程,求解即可.
8.【答案】C
【解析】【解答】解:∵OE、OF分别是∠AOC、∠BOC的平分线,
∴∠AOE=∠COE,∠COF=∠BOF,
∵∠AOC+∠COB=∠AOE+∠COE+∠COF+∠FOB=180°,
∴2(∠COE+∠COF)=180°,即∠COE+∠COF=90°,
则∠EOF=∠COE+∠COF=90°.
故选C.
【分析】由OE与OF为角平分线,利用角平分线定义得到两对角相等,由平角的定义及等式的性质即可求出所求角的度数.
9.【答案】A
【解析】【解答】解:∵AB=10cm,M是AB中点,
∴AM=BM=5cm
∵MN=3cm,
∴NB=MB-MN=5-3=2cm
故答案为:A.
【分析】首先根据线段中点的性质,得出AM=BM,然后根据MN,即可得出NB.
10.【答案】D
【解析】【解答】解:A选项,直线上不存在端点,不符合题意,选项错误;
B选项,经过A,B两点的线段不只一条,不符合题意,选项错误;
C选项,延长线段AB到C,则AC≠BC,不符合题意,选项错误;
D选项,反向延长线段BC到A,使得AB=BC,符合题意,选项正确。
故答案为:D。
【分析】依据直线、射线以及线段的相关概念进行解答即可。
11.【答案】105°
【解析】【解答】解:14点30分时即下午2点30分时,时针和分针中间相差3.5大格.
∵钟表12个数,每相邻两个数字之间的夹角为30°,
∴2点30分时分针与时针的夹角是3.5×30°=105°.
故答案是:105°.
【分析】本题注意,钟表上12个数字,每相邻两个数字之间的夹角为30°,14点30分时时针和分针中间相差3.5大格
12.【答案】两;两点确定一条直线
【解析】【解答】解:把一根木条钉牢在墙上,至少需要两枚钉子,其中的道理是:两点确定一条直线.
故答案为:两,两点确定一条直线.
【分析】根据两点确定一条直线解答.
13.【答案】2或6
【解析】【解答】解:①当点C在线段延长线上时,N与A点重合,
∵M、N分别是的中点,线段分别长,
∴,
∴;
②当点C在线段延长线上时,
∵M、N分别是的中点,线段分别长,
∴,
∴,
∴的值为或.
故答案为:2或6.
【分析】①当点C在线段BA延长线上时,N与A点重合,根据中点的概念可得AM=AB=2,BN=BC=4,然后根据MN=BN-AM进行计算;②当点C在线段AB延长线上时,根据中点的概念可得AM=AB=2,BN=BC=4,然后根据MN=AM+BN进行计算.
14.【答案】180
【解析】【解答】解:如右图所示,
∵∠AOD+∠COD=90°,∠COD+∠BOC=90°,∠BOD=∠COD+∠BOC,∠AOD+∠BOD=∠AOB,
∴∠AOD+∠COD+∠COD+∠BOC=180°,
∴∠AOD+2∠COD+∠BOC=180°,
∴∠AOB+∠COD=180°.
故答案是180.
【分析】先利用∠AOD+∠COD=90°,∠COD+∠BOC=90°,可得∠AOD+∠COD+∠COD+∠BOC=180°,而∠BOD=∠COD+∠BOC,∠AOD+∠BOD=∠AOB,于是有∠AOB+∠COD=180°.
15.【答案】解:设AB=6x,则BC=3x,AD=4x,
∵AD+AB+BC=DC,
∴4x+6x+3x=26,
解得x=2,
∴AB=12.
【解析】【分析】由于延长AB到C,反向延长AB到D,则AD+AB+BC=DC,再设AB=6x,则BC=3x,AD=4x,然后列方程4x+6x+3x=26,求出x即可得到线段AB的长.
16.【答案】解:∵AC=5.6cm,BC=2.4cm
∴AB=AC+BC=5.6+2.4=8
∵E为AC的中点,F为BC的中点,
∴AE=AC=×5.6=2.8,BF=BC=×2.4=1.2
∴EF=AB-AE-BF=8-2.8-1.2=4
答:EF的长为4cm.
【解析】【分析】根据已知线段的长求出AB的长,再根据线段中点的定义分别求出AE、BF的长,然后根据EF=AB-AE-BF,就可求出EF的长。
17.【答案】解:①如图1,射线OC在∠AOB的外部时,
∵∠AOB=60°,∠BOC=20°,
∴∠AOC=∠AOB+∠BOC=60°+20°=80°;
②射线OC在∠AOB的内部时,
∵∠AOB=60°,∠BOC=20°,
∴∠AOC=∠AOB﹣∠BOC=60°﹣20°=40°.
综上所示,∠AOC的度数为:80°或40°.
故答案为:80°或40°.
【解析】【分析】因为射线OC的位置不明确,所以分①射线OC在∠AOB的外部,②射线OC在∠AOB的内部两种情况进行讨论求解.
18.【答案】(1)∵AC=12,BC=8,M,N 分别是AC,BC的中点,
∴MC= AC,NC= BC,
∴MN= AC+ BC= ×12+ ×8=10.
(2)由(1)可知MN= AC+ BC= (AC+BC)= AB,
∵AB=a,
∴MN= a.
(3)设DE=x cm,则EF= DE= x cm,
EP= EF= x cm,DG=2x cm,DQ= DG=xcm.
∵PQ=18 cm,可得x+x+x=18,
解得x=8,
则DE=8 cm.
【解析】【分析】(1)由线段的中点可得MC= AC,NC= BC,由MN= AC+ BC即可求解;
(2)由(1)可知MN= AC+ BC= (AC+BC)= AB,继而得解;
(3)设DE=x cm,则EF= DE= x cm,EP= EF= x cm,DG=2x cm,DQ= DG=xcm.根据PQ=18 cm建立方程并解之即可.
19.【答案】(1)解:①如图所示;②如图所示;③如图所示;
(2)8
【解析】【解答】解:(2)以E为顶点的角中,小于平角的角有∠FEB,∠FED,∠FEG,∠FEH,∠CED,∠CEG,∠DEH,∠HEG,共8个.
故答案为:8.
【分析】(1)根据题意作图即可;
(2)根据平角的定义,再结合图形求解即可。
20.【答案】(1)解:如图:补全图形如下:
(2)解:∵线段AB=4,反向延长线段AB到C,使 ,
∴BC=10,
∵D是BC的中点,
∴BD= BC=5,
∵点E是BD的中点,
∴BE= BD= .
∴AE=AB BE=4 = ,
【解析】【分析】(1)由尺规作图画出符合题意的图,即可求解;
(2)根据线段的中点,线段的和差倍分计算出AE的长为 ,进行作答即可。
21.【答案】(1)解:设∠AOC的度数为x,则∠BOC的度数为2x,∠AOB的度数为3x,∠AOD的度数为
根据∠AOD-∠AOC=∠COD,得到方程 -x=18°,解得x=36°,
∴∠AOC的度数为36°。
(2)解:在(1)中方法可得∠AOC=2α
【解析】【分析】(1)可设∠AOC为x,即可表示出图中其余的角,根据∠COD的度数为18°,即可求得∠AOC的度数。
(2)根据(1)的证明方法同理可用α表示∠AOC。
22.【答案】(1)6
(2)解:由点D为BC的中点,得
BC=2CD=2BD,
由线段的和差,得
AB=AC+BC,即4CD+2CD=18,
解得CD=3,
AC=4CD=4×3=12cm;
(3)解:①当点E在线段AB上时,由线段的和差,得
BE=AB﹣AE=18﹣2=16cm,
②当点E在线段BA的延长线上,由线段的和差,得
BE=AB+AE=18+2=20cm.
综上所述:BE的长为16cm或20cm.
【解析】【解答】(1)图中有四个点,线段有=6.
故答案为6;
【分析】(1)求出=6即可作答;
(2)先求出 BC=2CD=2BD, 再求出CD=3,最后求出AC的值即可;
(3)分类讨论,根据 EA=2cm求解即可。
23.【答案】(1)解: ,OE平分 ,
,
(2)解:∵ ,
∴∠EOF=90°,
∵ ,
∴∠DOF=90°-35°=55°,
∴∠COF=180°-55°=125°.
【解析】【分析】(1)根据对顶角相等的性质和角平分线的定义可得∠DOE的度数,再根据邻补角的定义求解即可;
(2)根据垂直的定义和(1)题求得的∠DOE可得∠DOF的度数,然后根据领补角的定义求解即可。
24.【答案】(1)∠BOC;∠EOD
(2)证明:∵∠COD=90°,
∴∠COE+∠EOD=90°,
∴∠AOC+∠BOD=180°-∠COD=90°,
∵OD平分∠BOE,
∴∠EOD=∠BOD,
∴∠COE=∠AOC,
∴OC平分∠AOE
(3)解:∠AOC=2∠DOE.理由如下:
∵OE平分∠BOC,
∴∠BOC=2∠COE,
又∵∠AOC=180°-∠BOC,
∴∠AOC=180°-2∠COE,
∵∠COD=90°,
∴∠DOE+∠COE=90°,
∴∠DOE=90°-∠COE,
∴2∠DOE=180°-2∠COE,
∴∠AOC=2∠DOE.
【解析】【解答】(1)解:∵∠AOC+∠BOC=180°,
∴∠AOC的补角是∠BOC;
∵∠COD=90°,
∴∠COE+∠EOD=90°,
∴∠COE的余角是∠EOD;
故答案为:∠BOC,∠EOD;
【分析】(1)根据互为余角、互为补角的意义,即可得出结论;
(2)根据角平分线的性质即可得出结论;
(3)根据角平分线的性质即可得出结论。
1 / 1
一、单选题
1.如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形的是( )
A. B.
C. D.
2.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是( )
A.以点C为圆心,OD为半径的弧 B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧 D.以点E为圆心,DM为半径的弧
3.如图,点 是 的中点,点 是 的中点,则下列等式中正确的有( )
①②③④
A.4个 B.3个 C.2个 D.1个
4. 把一副三角板按如图所示拼在一起,则等于( )
A. B. C. D.
5.若一个n边形从一个顶点最多能引出5条对角线,则n是( )
A.5 B.8 C.9 D.10
6.下列说法中正确的是( )
A.两个半圆是等弧
B.过圆内一点仅可以作出1条圆的最长弦
C.相等的圆心角所对的弧相等
D.同圆中优弧与半圆的差必是劣弧
7.数轴上表示﹣1的点到表示x的距离为3,则x表示的数为( )
A.2 B.﹣2 C.﹣4 D.2或﹣4
8.如图,O为直线AB上一点,OE、OF分别是∠AOC、∠BOC的平分线,则∠EOF的度数是( )
A.60° B.80° C.90° D.100°
9.如图,已知线段AB=10cm,M是AB中点,点N在AB上,MN=3cm,那么线段NB的长为( )
A.2cm B.3cm C.5cm D.8cm
10.以下说法正确的是( ).
A.直线l上有两个端点 B.经过A,B两点的线段只有一条
C.延长线段AB到C,使AC=BC D.反向延长线段BC至A,使AB=BC
二、填空题
11.时钟在14点30分时,这时刻钟面上时针与分针夹角的度数为 .
12.要把一根木条在墙上钉牢,至少需要 枚钉子.其中的道理是
13.直线l上的线段分别长,M、N分别是的中点,则 .
14.如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 度.
三、解答题
15.已知线段AB,延长AB到C,使BC=AB,再反向延长AB到D,使AD=AB.若CD=26cm,求线段AB的长.
16.已知线段AC和BC在一条直线上,如果AC=5.6cm,BC=2.4cm,E为AC的中点,F为BC的中点,求EF的长.
17.已知一条射线OA,如果从点O再引两条射线OB和OC,使∠AOB=60°,∠BOC=20°,求∠AOC的度数.
18. 如图,已知点C在线段AB上,M,N分别是AC,BC的中点.
(1)若线段AC=12,BC=8,求线段MN的长度.
(2)设AB=a,求线段MN的长度.
(3)解决问题:已知线段DE,延长DE到F,使EF= DE;延长ED到G,使DG=2DE,P,Q分别是EF,DG的中点.若PQ=18 cm,求DE的长.
四、作图题
19.如图,平面上有四个点A,B,C,D.
(1)根据下列语句画图:
①射线BA;
②直线AD,BC相交于点E;
③在线段DC的延长线上取一点F,使CF=BC,连接EF.
(2)图中以E为顶点的角中,小于平角的角共有 个.
20.已知线段AB,反向延长线段AB到C,使 ,D为BC的中点,E为BD的中点.
(1)补全图形;
(2)若 ,求AE的长度.
21.如图所示,已知∠BOC=2∠AOC,OD平分∠AOB,
(1)若∠COD=18°,求∠AOC的度数.
(2)若∠COD=α,试用α表示∠AOC.
22.如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
23.如图,两直线 相交于点 , 平分 ,如果 .
(1)求 ;
(2)若 ,求 .
24.综合与探究
数学活动课上,老师提出如下问题:如图1,将含30°的三角尺COD的直角顶点O放在直线AB上,三角尺COD中,∠COD=90°,∠C=60°,∠D=30°.过点O作射线OE.
(1)∠AOC的补角是 ,∠COE的余角是 ;(直接写回答案)
(2)如图2,“启航”小组根据学习几何积累的活动经验:特殊的位置可以得到特殊的结论,在图1的基础上继续展开探究,他们提出的问题是:调整三角尺的位置,当OD平分∠BOE时,OC平分∠AOE.请你证明启航小组提出的问题;
(3)如图3,受到“启航”小组的启发,“睿智”小组提出的问题是:在图2的基础上,继续调整三角尺的位置,当OE平分∠BOC时,∠AOC与∠DOE有怎样的数量关系?请说明理由.
答案解析部分
1.【答案】D
【解析】【解答】解:A、以O为顶点的角不止一个,不能用∠O表示,故A选项不符合题意;
B、以O为顶点的角不止一个,不能用∠O表示,故B选项不符合题意;
C、以O为顶点的角不止一个,不能用∠O表示,故C选项不符合题意;
D、能用∠1,∠AOB,∠O三种方法表示同一个角,故D选项符合题意.
故答案为:D.
【分析】根据角的四种表示方法和具体要求回答即可.
2.【答案】D
【解析】【解答】解:根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧
故答案为:D
【分析】根据尺规作图,作一个角等于已知角可知弧FG是以点E为圆心,DM为半径的弧.
3.【答案】C
【解析】【解答】∵点 是 的中点,点 是 的中点,
∴AC=BC,CD=BD,
∵CD=CB-BD=AC-BD,
∴①符合题意,
∵AD-BC=AC+CD-BC=CD,
∴②符合题意,
∵2AD-AB=2AC+2CD-AB=2CD=2BD ,
∴③不符合题意,
∵CD= BC, BC= AB,即CD= AB,
∴④不符合题意,
综上只有两个是正确的,
故答案为:C.
【分析】根据线段的中点,即可找到线段之间的数量关系.
4.【答案】D
【解析】【解答】解:三角板的六个角分别为:90°,45°,45°,90°,60°,30°
如图拼接,可得∠ABC=30°+90°=120°
故答案为:D
【分析】本题考查三角形角度的计算,熟悉三角板的角度是关键。
5.【答案】B
【解析】【解答】解:根据题意可得:n-3=5,
解得:n=8.
故答案为:B.
【分析】从n边形的一个顶点作对角线的条数为(n-3)条,据此求解.
6.【答案】D
【解析】【解答】解:A、在同圆或等圆中,两个半圆是等弧,故原题说法错误;
B、过圆内一点(此点不是圆心)仅可以作出1条圆的最长弦,故原题说法错误;
C、在同圆或等圆中,相等的圆心角所对的弧相等,故原题说法错误;
D、同圆中优弧与半圆的差必是劣弧,说法正确;
故选:D.
【分析】根据圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆,大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧,连接圆上任意两点的线段叫弦的相关定义分别进行分析即可.
7.【答案】D
【解析】【解答】解:由题意得:|x﹣(﹣1)|=3,
∴|x+1|=3,
∴x+1=±3,
∴x=2或﹣4.
故答案为:D.
【分析】数轴上任意两点间的距离等于这两点所表示数差的绝对值,据此列出方程,求解即可.
8.【答案】C
【解析】【解答】解:∵OE、OF分别是∠AOC、∠BOC的平分线,
∴∠AOE=∠COE,∠COF=∠BOF,
∵∠AOC+∠COB=∠AOE+∠COE+∠COF+∠FOB=180°,
∴2(∠COE+∠COF)=180°,即∠COE+∠COF=90°,
则∠EOF=∠COE+∠COF=90°.
故选C.
【分析】由OE与OF为角平分线,利用角平分线定义得到两对角相等,由平角的定义及等式的性质即可求出所求角的度数.
9.【答案】A
【解析】【解答】解:∵AB=10cm,M是AB中点,
∴AM=BM=5cm
∵MN=3cm,
∴NB=MB-MN=5-3=2cm
故答案为:A.
【分析】首先根据线段中点的性质,得出AM=BM,然后根据MN,即可得出NB.
10.【答案】D
【解析】【解答】解:A选项,直线上不存在端点,不符合题意,选项错误;
B选项,经过A,B两点的线段不只一条,不符合题意,选项错误;
C选项,延长线段AB到C,则AC≠BC,不符合题意,选项错误;
D选项,反向延长线段BC到A,使得AB=BC,符合题意,选项正确。
故答案为:D。
【分析】依据直线、射线以及线段的相关概念进行解答即可。
11.【答案】105°
【解析】【解答】解:14点30分时即下午2点30分时,时针和分针中间相差3.5大格.
∵钟表12个数,每相邻两个数字之间的夹角为30°,
∴2点30分时分针与时针的夹角是3.5×30°=105°.
故答案是:105°.
【分析】本题注意,钟表上12个数字,每相邻两个数字之间的夹角为30°,14点30分时时针和分针中间相差3.5大格
12.【答案】两;两点确定一条直线
【解析】【解答】解:把一根木条钉牢在墙上,至少需要两枚钉子,其中的道理是:两点确定一条直线.
故答案为:两,两点确定一条直线.
【分析】根据两点确定一条直线解答.
13.【答案】2或6
【解析】【解答】解:①当点C在线段延长线上时,N与A点重合,
∵M、N分别是的中点,线段分别长,
∴,
∴;
②当点C在线段延长线上时,
∵M、N分别是的中点,线段分别长,
∴,
∴,
∴的值为或.
故答案为:2或6.
【分析】①当点C在线段BA延长线上时,N与A点重合,根据中点的概念可得AM=AB=2,BN=BC=4,然后根据MN=BN-AM进行计算;②当点C在线段AB延长线上时,根据中点的概念可得AM=AB=2,BN=BC=4,然后根据MN=AM+BN进行计算.
14.【答案】180
【解析】【解答】解:如右图所示,
∵∠AOD+∠COD=90°,∠COD+∠BOC=90°,∠BOD=∠COD+∠BOC,∠AOD+∠BOD=∠AOB,
∴∠AOD+∠COD+∠COD+∠BOC=180°,
∴∠AOD+2∠COD+∠BOC=180°,
∴∠AOB+∠COD=180°.
故答案是180.
【分析】先利用∠AOD+∠COD=90°,∠COD+∠BOC=90°,可得∠AOD+∠COD+∠COD+∠BOC=180°,而∠BOD=∠COD+∠BOC,∠AOD+∠BOD=∠AOB,于是有∠AOB+∠COD=180°.
15.【答案】解:设AB=6x,则BC=3x,AD=4x,
∵AD+AB+BC=DC,
∴4x+6x+3x=26,
解得x=2,
∴AB=12.
【解析】【分析】由于延长AB到C,反向延长AB到D,则AD+AB+BC=DC,再设AB=6x,则BC=3x,AD=4x,然后列方程4x+6x+3x=26,求出x即可得到线段AB的长.
16.【答案】解:∵AC=5.6cm,BC=2.4cm
∴AB=AC+BC=5.6+2.4=8
∵E为AC的中点,F为BC的中点,
∴AE=AC=×5.6=2.8,BF=BC=×2.4=1.2
∴EF=AB-AE-BF=8-2.8-1.2=4
答:EF的长为4cm.
【解析】【分析】根据已知线段的长求出AB的长,再根据线段中点的定义分别求出AE、BF的长,然后根据EF=AB-AE-BF,就可求出EF的长。
17.【答案】解:①如图1,射线OC在∠AOB的外部时,
∵∠AOB=60°,∠BOC=20°,
∴∠AOC=∠AOB+∠BOC=60°+20°=80°;
②射线OC在∠AOB的内部时,
∵∠AOB=60°,∠BOC=20°,
∴∠AOC=∠AOB﹣∠BOC=60°﹣20°=40°.
综上所示,∠AOC的度数为:80°或40°.
故答案为:80°或40°.
【解析】【分析】因为射线OC的位置不明确,所以分①射线OC在∠AOB的外部,②射线OC在∠AOB的内部两种情况进行讨论求解.
18.【答案】(1)∵AC=12,BC=8,M,N 分别是AC,BC的中点,
∴MC= AC,NC= BC,
∴MN= AC+ BC= ×12+ ×8=10.
(2)由(1)可知MN= AC+ BC= (AC+BC)= AB,
∵AB=a,
∴MN= a.
(3)设DE=x cm,则EF= DE= x cm,
EP= EF= x cm,DG=2x cm,DQ= DG=xcm.
∵PQ=18 cm,可得x+x+x=18,
解得x=8,
则DE=8 cm.
【解析】【分析】(1)由线段的中点可得MC= AC,NC= BC,由MN= AC+ BC即可求解;
(2)由(1)可知MN= AC+ BC= (AC+BC)= AB,继而得解;
(3)设DE=x cm,则EF= DE= x cm,EP= EF= x cm,DG=2x cm,DQ= DG=xcm.根据PQ=18 cm建立方程并解之即可.
19.【答案】(1)解:①如图所示;②如图所示;③如图所示;
(2)8
【解析】【解答】解:(2)以E为顶点的角中,小于平角的角有∠FEB,∠FED,∠FEG,∠FEH,∠CED,∠CEG,∠DEH,∠HEG,共8个.
故答案为:8.
【分析】(1)根据题意作图即可;
(2)根据平角的定义,再结合图形求解即可。
20.【答案】(1)解:如图:补全图形如下:
(2)解:∵线段AB=4,反向延长线段AB到C,使 ,
∴BC=10,
∵D是BC的中点,
∴BD= BC=5,
∵点E是BD的中点,
∴BE= BD= .
∴AE=AB BE=4 = ,
【解析】【分析】(1)由尺规作图画出符合题意的图,即可求解;
(2)根据线段的中点,线段的和差倍分计算出AE的长为 ,进行作答即可。
21.【答案】(1)解:设∠AOC的度数为x,则∠BOC的度数为2x,∠AOB的度数为3x,∠AOD的度数为
根据∠AOD-∠AOC=∠COD,得到方程 -x=18°,解得x=36°,
∴∠AOC的度数为36°。
(2)解:在(1)中方法可得∠AOC=2α
【解析】【分析】(1)可设∠AOC为x,即可表示出图中其余的角,根据∠COD的度数为18°,即可求得∠AOC的度数。
(2)根据(1)的证明方法同理可用α表示∠AOC。
22.【答案】(1)6
(2)解:由点D为BC的中点,得
BC=2CD=2BD,
由线段的和差,得
AB=AC+BC,即4CD+2CD=18,
解得CD=3,
AC=4CD=4×3=12cm;
(3)解:①当点E在线段AB上时,由线段的和差,得
BE=AB﹣AE=18﹣2=16cm,
②当点E在线段BA的延长线上,由线段的和差,得
BE=AB+AE=18+2=20cm.
综上所述:BE的长为16cm或20cm.
【解析】【解答】(1)图中有四个点,线段有=6.
故答案为6;
【分析】(1)求出=6即可作答;
(2)先求出 BC=2CD=2BD, 再求出CD=3,最后求出AC的值即可;
(3)分类讨论,根据 EA=2cm求解即可。
23.【答案】(1)解: ,OE平分 ,
,
(2)解:∵ ,
∴∠EOF=90°,
∵ ,
∴∠DOF=90°-35°=55°,
∴∠COF=180°-55°=125°.
【解析】【分析】(1)根据对顶角相等的性质和角平分线的定义可得∠DOE的度数,再根据邻补角的定义求解即可;
(2)根据垂直的定义和(1)题求得的∠DOE可得∠DOF的度数,然后根据领补角的定义求解即可。
24.【答案】(1)∠BOC;∠EOD
(2)证明:∵∠COD=90°,
∴∠COE+∠EOD=90°,
∴∠AOC+∠BOD=180°-∠COD=90°,
∵OD平分∠BOE,
∴∠EOD=∠BOD,
∴∠COE=∠AOC,
∴OC平分∠AOE
(3)解:∠AOC=2∠DOE.理由如下:
∵OE平分∠BOC,
∴∠BOC=2∠COE,
又∵∠AOC=180°-∠BOC,
∴∠AOC=180°-2∠COE,
∵∠COD=90°,
∴∠DOE+∠COE=90°,
∴∠DOE=90°-∠COE,
∴2∠DOE=180°-2∠COE,
∴∠AOC=2∠DOE.
【解析】【解答】(1)解:∵∠AOC+∠BOC=180°,
∴∠AOC的补角是∠BOC;
∵∠COD=90°,
∴∠COE+∠EOD=90°,
∴∠COE的余角是∠EOD;
故答案为:∠BOC,∠EOD;
【分析】(1)根据互为余角、互为补角的意义,即可得出结论;
(2)根据角平分线的性质即可得出结论;
(3)根据角平分线的性质即可得出结论。
1 / 1
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
