京改版八年级数学下册第十二章三角形 单元复习题(含解析)
文档属性
| 名称 | 京改版八年级数学下册第十二章三角形 单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 774.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览


文档简介
京改版八年级数学下册第十二章三角形单元复习题
一、单选题
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.下列各组数中能作为直角三角形的三边长的是( )
A.6,7,8 B.5,6,7 C.4.5,6,7.5 D.4,5,6
3.如图,点A,E,F,D在同一直线上,若AB∥CD,AB=CD,AE=FD,则图中的全等三角形有 ( )
A.1对 B.2对 C.3对 D.4对
4.下图所示的五角星是用螺栓将两端打有孔的5根木条连接构成的图形,它的形状不稳定。如果在木条交叉点打孔加装螺栓的办法使其形状稳定,那么至少需要添加( )个螺栓。
A.1 B.2 C.3 D.4 。
5.下列各组数可以是一个三角形的三边长的是( )
A.1,1,2 B.3,4,5 C.5,7,12 D.10,11,22
6.在Rt△ABC中,CD是斜边AB上的中线,则以下判断正确的是( )
A.BC=2CD B.CD=2AB C.AC=2CD D.CD=BD
7.如图,在△ABC中,AC=AB,∠BAC=90°,BD平分∠ABC,与AC相交于点F,CD⊥BD,垂足为D,交BA的延长线于点E,AH⊥BC交BD于点M,交BC于点H,下列选项不正确的是( )
A.∠E=67.5° B.∠AMF=∠AFM
C.BF=2CD D.BD=AB+AF
8.如图,在已知的△ABC中,按以下步骤作图:
①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
A.50° B.45° C.30° D.25°
9.如图,在△ABC中,∠C=90°,AD是△ABC的一条角平分线.若AC=6,AB=10,则点D到AB边的距离为( )
A.2 B.2.5 C.3 D.4
10.如图所示,在等边三角形ABC中,D,E分别在边AB,BC上,且,AE与CD交于点F,,垂足为点G.下列结论:①;②;③是等边三角形;④,其中正确结论的个数是( )
A.3 B.2 C.1 D.0
11.如图,直角△ADB中,∠D=90°,C为AD上一点,且∠ACB的度数为 ,则 的值可能是( )
A.10 B.20 C.30 D.40
二、填空题
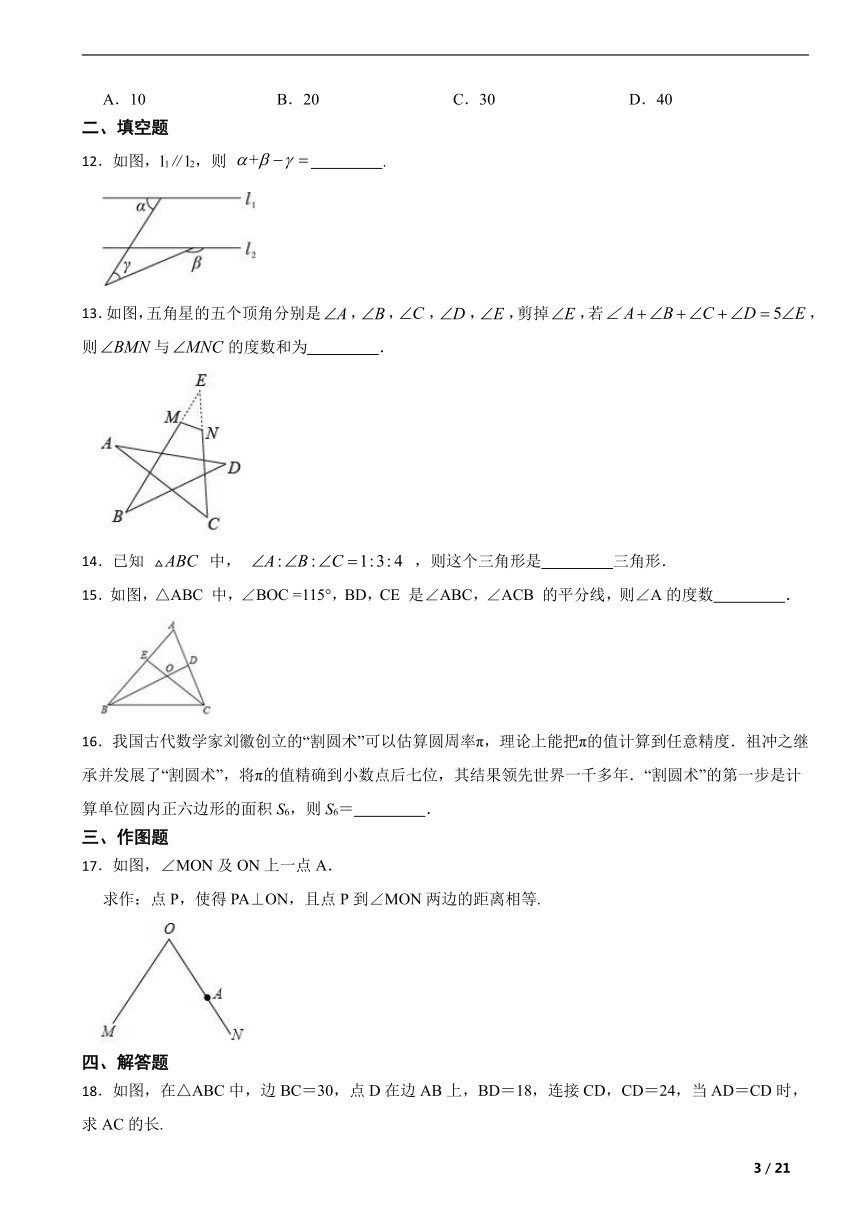
12.如图,l1∥l2,则 .
13.如图,五角星的五个顶角分别是,,,,,剪掉,若,则与的度数和为 .
14.已知 中, ,则这个三角形是 三角形.
15.如图,△ABC
中,∠BOC =115°,BD,CE 是∠ABC,∠ACB 的平分线,则∠A的度数 .
16.我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内正六边形的面积S6,则S6= .
三、作图题
17.如图,∠MON及ON上一点A.
求作:点P,使得PA⊥ON,且点P到∠MON两边的距离相等.
四、解答题
18.如图,在△ABC中,边BC=30,点D在边AB上,BD=18,连接CD,CD=24,当AD=CD时,求AC的长.
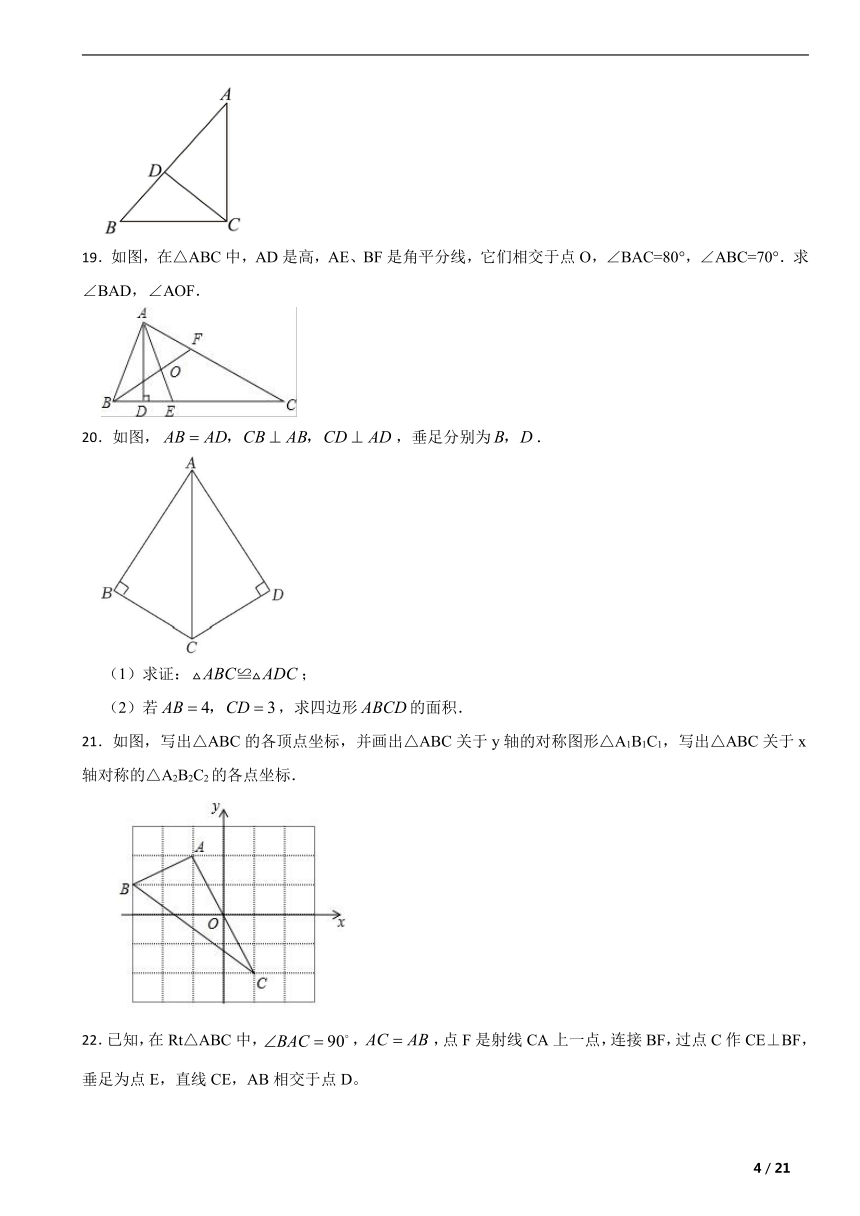
19.如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=80°,∠ABC=70°.求∠BAD,∠AOF.
20.如图,,垂足分别为.
(1)求证:;
(2)若,求四边形的面积.
21.如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴的对称图形△A1B1C1,写出△ABC关于x轴对称的△A2B2C2的各点坐标.
22.已知,在Rt△ABC中,,,点F是射线CA上一点,连接BF,过点C作CE⊥BF,垂足为点E,直线CE,AB相交于点D。
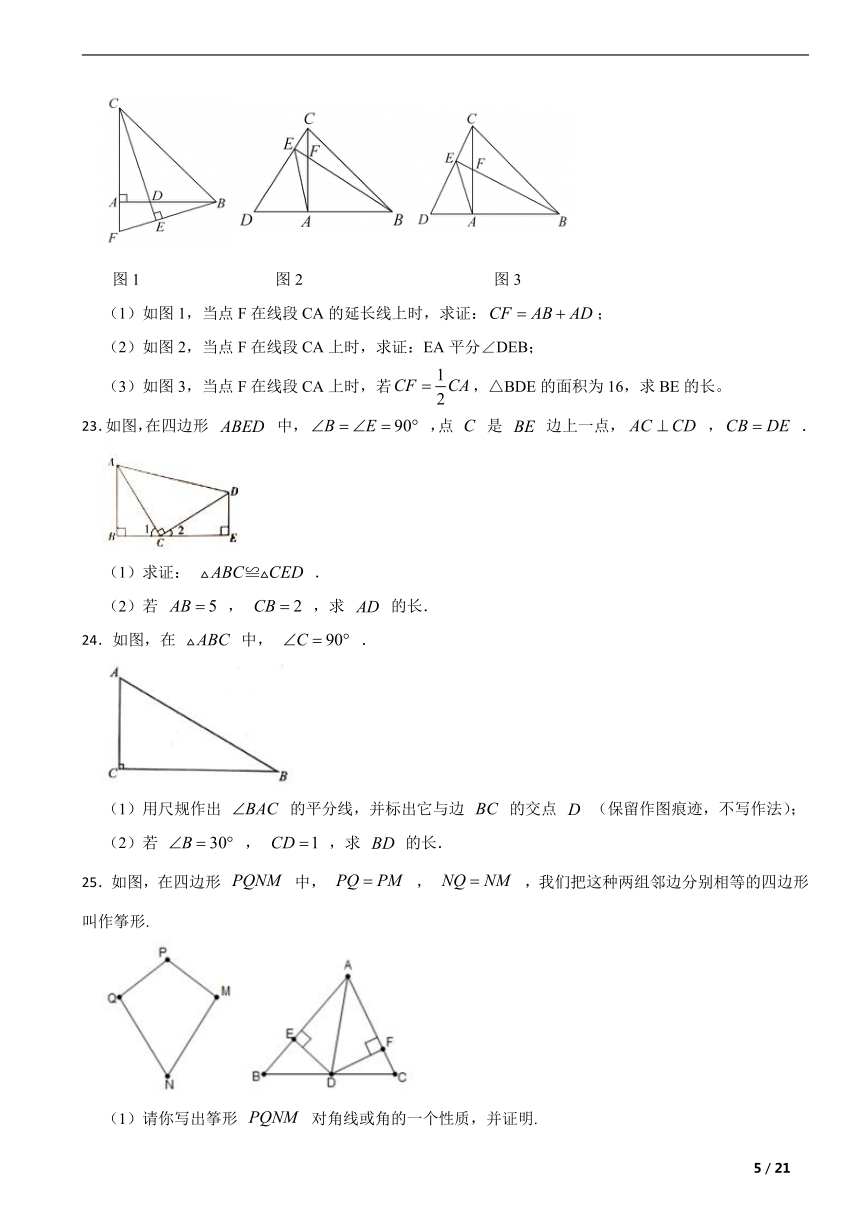
图1 图2 图3
(1)如图1,当点F在线段CA的延长线上时,求证:;
(2)如图2,当点F在线段CA上时,求证:EA平分∠DEB;
(3)如图3,当点F在线段CA上时,若,△BDE的面积为16,求BE的长。
23.如图,在四边形 中, ,点 是 边上一点, , .
(1)求证: .
(2)若 , ,求 的长.
24.如图,在 中, .
(1)用尺规作出 的平分线,并标出它与边 的交点 (保留作图痕迹,不写作法);
(2)若 , ,求 的长.
25.如图,在四边形 中, , ,我们把这种两组邻边分别相等的四边形叫作筝形.
(1)请你写出筝形 对角线或角的一个性质,并证明.
(2)如图, 是 的角平分线, , ,垂足分别为 , .请判断四边形 是否为筝形,证明你的结论.
26.在中,平分,平分,和交于点,其中令,.
(1)【计算求值】如图,如果,则 ;
如果,则 .
(2)【猜想证明】如图2请你根据(1)中【计算求值】的心得猜想写出与的关系式为 ,并请你说明你的猜想的正确性.
(3)【解决问题】如图3,某校园内有一个如图2所示的三角形的小花园,花园中有两条小路,和为三角形的角平分线,交点为点,在处建有一个自动浇水器,需要在边取一处接水口,经过测量得知,米,米,请你求出水管至少要多长?结果取整数
答案解析部分
1.【答案】A
【解析】【解答】A、不是轴对称图形,故本选项符合题意;
B、是轴对称图形,故本选项不符合题意;
C、是轴对称图形,故本选项不符合题意;
D、是轴对称图形,故本选项不符合题意.
故答案为:A.
【分析】根据轴对称图形的定义逐项判断即可。
2.【答案】C
【解析】【解答】解:A、
,不符合题意;
B、
,不符合题意;
C、
,符合题意;
D、
,不符合题意;
故答案为:C.
【分析】根据勾股定理的逆定理逐项判断即可。
3.【答案】C
【解析】【解答】解:∵AE=DF,
∴AE+EF=DF+EF,
∴AF=DE,
∵AB∥CD,
∴∠A=∠D,
在△BAF和△CDE中,
,
∴△BAF≌△CDE(SAS),
在△BAE和△CDF中,
,
∴△BAE≌△CDF(SAS),
∴BE=CF,∠AEB=∠DFC,
∴∠BEF=∠CFE,
在△BEF和△CFE中,
,
∴△BEF≌△CFE(SAS),
即全等三角形有3对,
故C符合题意.
故答案为:C.
【分析】根据题意可得出AF=DE,∠A=∠D,利用SAS分别得出△BAF≌△CDE和△BAE≌△CDF,再由全等三角形的性质证得∠BEF=∠CFE,利用SAS证得△BEF≌△CFE,从而得到答案.
4.【答案】A
【解析】【解答】解 :
A点加上了螺栓后,根据三角形的稳定性,原不稳定的五角星就具有稳定性了。
故应选 :A.
【分析】根据三角形的稳定性,在A处打上螺栓,五角星的各边就固定了。
5.【答案】B
【解析】【解答】解: A、∵1+1=2 , 不能组成三角形,故A选项不符合题意;
B、 , 能组成三角形,故B选项符合题意;
C、 , 不能组成三角形,故C选项不符合题意;
D、 , 能组成三角形,故D选项不符合题意.
故答案为:B.
【分析】根据三角形三边关系,只需要判断较小两边的和是否大于较大边长即可.
6.【答案】D
【解析】【解答】解:∵CD是斜边AB的中线,
∴AB=2CD,故A、B、C不符合题意;
∴CD=BD,故D符合题意;
故答案为:D.
【分析】利用直角三角形斜边上的中线等于斜边的一半,可得到AB=2CD,CD=BD=AD,由此可得到正确结论的选项.
7.【答案】D
【解析】【解答】解:A、∵AC=AB,∠BAC=90°,∴∠B=45°,∴∠DBE=22.5°,
∴∠E=90°-∠DBE=90°-22.5°=67.5°,正确,不符合题意;
B、∵∠B=45°,∴∠BAH=∠ACB=90°-∠B=45°,∴∠AMF=∠ABM+∠BAM
=22.5°+45°=67.5°,∠AFM=∠ACB+∠CBF=45°+22.5°=67.5°,正确,符合题意;
CD、∵AB=AC,∠BAC=∠EAC=90°,∠AFB=∠CFD,∴∠ABF=∠FCD,∴△ABF≌△ACE(ASA),∴AF=AE,∴AB+AF=AB+AE=BE>BD,D错误,符合题意;∵BD平分∠ABC,BD⊥EC,∴△ABC是等腰三角形,∴ED=CD,∴EC=2CD,∵△ABF≌△ACE,∴BF=EC,∴BF=2CD,∴C正确,不符合题意.
故答案为:D.
【分析】根据等腰三角形的性质,结合三角形外角的性质可求∠E、∠AMF和∠AFM的度数;利用角边角定理可证△ABF≌△ACE,得出对应边相等,再结合直角三角形斜边最大可得BD8.【答案】D
【解析】【解答】解:∵根据题意得出MN是线段BC的垂直平分线,
∴CD=BD,即∠B=∠BCD.
∵CD=AC,
∴∠CDA=∠A=50°,
∵∠B+∠BCD=∠CAD,
∴∠B= ∠CDA=25°.
故答案为:D.
【分析】由作图痕迹可知MN是线段BC的垂直平分线,然后利用中垂线的性质和等腰三角形的性质求得∠B=∠BCD,∠CDA=∠A=50°,最后利用三角形外角的性质求解.
9.【答案】C
【解析】【解答】解:作DE⊥AB于E,如图,
在Rt△ABC中,BC= =8,
∵AD是△ABC的一条角平分线,DC⊥AC,DE⊥AB,
∴DE=DC,
设DE=DC=x,
S△ABD= DE AB= AC BD,
即10x=6(8﹣x),解得x=3,
即点D到AB边的距离为3.
故答案为C.
【分析】作DE⊥AB于E,由勾股定理计算出可求BC=8,再利用角平分线的性质得到DE=DC,设DE=DC=x,利用等等面积法列方程、解方程即可解答.
10.【答案】A
【解析】【解答】解:∵等边,
∴,,
∵,
∴,
∴,①正确;
∴,
∴,
在中,
,②正确;
∵,,
∴,
∴不是等腰三角形,③错误;
∵,,
∴,
∴,
∴,④正确,
综上所述,正确的有①②④.
故答案为:A
【分析】先根据等边三角形的性质得到,,进而运用三角形全等的判定与性质证明即可判断①;进而根据题意进行角的运算即可判断②;从而结合等腰三角形的判定即可判断③;再结合题意进行角的运算,运用含30°角的直角三角形的性质即可判断④。
11.【答案】C
【解析】【解答】∠ACB=∠90°+∠CBD
∴(5x 10)°=∠90°+∠CBD
化简得:x=20+ ∠DBC
∵0°<∠DBC<90°
∴20°故答案为:C
【分析】根据三角形的外角性质和三角形内角∠DBC的取值范围得出x的范围。
12.【答案】180°
【解析】【解答】如图:
∵l1∥l2,∴ ,
∵ 是三角形的一个外角,∴ ,
∵ 与 是邻补角,∴ ,
∴ ,即:
∴
故答案为:
【分析】根据两直线平行同位角相等、三角形外角定理以及邻补角的概念列式计算即可;
13.【答案】
【解析】【解答】如图,
∵∠1=∠B+∠D,∠2=∠A+∠C,
∴∠1+∠2=
∵∠1+∠2+
=180°
∴6
=180°
∴=30°
∵∠BMN+∠MNC
=∠4+∠E+∠3+∠E
=180°+∠E
=180°+30°
=210°.
故答案为:
.
【分析】根据三角形外角和性质:∠1+∠2=
,根据三角形内角定理:∠1+∠2+
=180°,求得
,再根据∠BMN+∠MNC=∠4+∠E+∠3+∠E可得。
14.【答案】直角
【解析】【解答】解:设∠A、∠B、∠C分别为α、3α、4α,
则α+3α+4α=180°,
解得α=22.5°,
所以,∠C=4×22.5°=90°,
这个三角形是直角三角形.
故答案为:直角.
【分析】根据比设∠A、∠B、∠C分别为α、3α、4α,然后根据三角形的内角和等于180°列式求出∠C,作出判断即可.
15.【答案】50°
【解析】【解答】解:∵∠BOC =115°,
∴∠OBC+∠OCB=180°-115°=65°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC= ∠ABC,∠OCB= ∠ACB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=130°,
∴∠A=180°-130°=50°,
故答案为:50°.
【分析】利用角平分线的性质得到角的关系,再利用三角形的内角和求解即可。
16.【答案】
【解析】【解答】解:如图所示,
单位圆的半径为1,则其内接正六边形ABCDEF中,
△AOB是边长为1的正三角形,
所以正六边形ABCDEF的面积为
S6=6× ×1×1×sin60°= .
故答案为: .
【分析】根据题意画出图形,结合图形求出单位圆的内接正六边形的面积.
17.【答案】解:如图所示,点P即为所求.
【解析】【分析】过点A作AP⊥ON,交∠MON 的平分线于点P.
18.【答案】解:
为直角三角形,
在中
【解析】【分析】由勾股定理逆定理知△BCD为直角三角形,且∠BDC=90°,由题意可得AD=CD=24,然后在Rt△ADC中,利用勾股定理计算即可.
19.【答案】解:∵AD是高,∠ABC=70°,
∴∠BAD=90°﹣70°=20°,
∵AE、BF是角平分线,∠BAC=80°,∠ABC=70°,
∴∠ABO=35°,∠BAO=40°,
∴∠AOF=∠ABO+∠BAO=75°
【解析】【分析】在直角三角形中,根据两锐角互余即可得到∠BAD=20°,根据角平分线的性质可求出∠BAO和∠ABO,最后由三角形外角的性质求得∠AOF=75°.
20.【答案】(1)证明:在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC(HL);
(2)解:由(1)知:△ABC≌△ADC,
∴BC=CD=3,S△ABC=S△ADC,
∴S△ABC=AB BC=×4×3=6,
∴S△ADC=6,
∴S四边形ABCD=S△ABC+S△ADC=12,
答:四边形ABCD的面积是12.
【解析】【分析】(1)根据三角形全等的判定证明Rt△ABC≌Rt△ADC(HL)即可求解;
(2)根据三角形全等的性质得到BC=CD=3,S△ABC=S△ADC,进而结合题意运用S四边形ABCD=S△ABC+S△ADC即可求解。
21.【答案】解:△ABC的各顶点坐标:A(﹣1,2),B(﹣3,1),C(1,﹣2);
△A1B1C1如图所示:
△ABC关于x轴对称的△A2B2C2的各点坐标:A2(﹣1,-2),B2(﹣3,﹣1),C2(1,2).
【解析】【分析】根据平面直角坐标系写出点A、B、C的坐标即可;
先找出点A、B、C关于y轴的对称点A1、B1、C1的位置,然后顺次连接即可;
根据关于x轴对称的点的横坐标不变,纵坐标互为相反数解答.
22.【答案】(1)证明:∵CE⊥BF,
∴∠CEB=90°,
∴∠CEB=∠BAC=90°,
∴∠ACD+∠CDA=∠ABF+∠EDB.
∵∠CDA=∠EDB,
∴∠ACD=∠ABF.
∵∠ACD=∠ABF,AC=AB,∠CAD=∠BAF,
∴△ACD≌△ABF(ASA),
∴AF=AD,
∴CF=AC+AF=AC+AD=AB+AD.
(2)证明:过A作AM⊥CD于点M,AN⊥BE于点N,则∠CMA=∠ANB=90°.
∵∠CEF=∠CAB=90°,∠CFE=∠BFA,
∴∠MCA=∠NBA.
∵∠MCA=∠NBA,∠CMA=∠ANB,AC=AB,
∴△ACM≌△ABN(AAS),
∴AM=AN,
∴EA平分∠DEB.
(3)解:∵ ∠CEB=∠CAB=90°,∠CFE=∠AFB,
∴△ECF=∠FBA.
∵∠CAD=∠BED=90°,AC=BC,∠DCA=∠FBA,
∴△ABF≌△ACD(ASA),
∴AF=AD.
∵CF=CA,
∴CF=AF=AD=AC=AB.
过E作EG⊥BD于点G,
∵S△ABE=AB·EG,S△ADE=AD·EG,
∴S△ABE=2S△ADE.
∵S△BDE=16,
∴S△ABE=,S△ADE=.
过A作AM⊥CD于点M,AN⊥BE于点N,
∴S△ADE=AM·DE,S△ABE=AN·BE.
由(2)得AM=AN,
∴BE=2DE.
设DE=x,则BE=2x.
∵S△BDE=16,
∴DE·BE=16,
∴x·2x=16,
∴x=4,
∴BE=8.
【解析】【分析】(1)由垂直的定义可得∠CEB=∠BAC=90°,由等角的余角相等可得∠ACD=∠ABF,利用ASA证明△ACD≌△ABF,得到AF=AD,据此解答;
(2)过A作AM⊥CD于点M,AN⊥BE于点N,则∠CMA=∠ANB=90°,同理证明△ACM≌△ABN,得到AM=AN,据此证明;
(3)利用ASA证明△ABF≌△ACD,得到AF=AD,结合已知条件可得CF=AF=AD=AC=AB,过E作EG⊥BD于点G,由三角形的面积公式可得S△ABE=2S△ADE,进而推出BE=2DE,设DE=x,则BE=2x,根据S△BDE=DE·BE=16可得x的值,进而可求出BE的长.
23.【答案】(1)证明:∵ ,
∴ .
∵ ,
∴ ,
∴ .
在 和 中,
.
(2)解:∵ ,
∴ , .
∵ ,
∴在 中, ,
∵ ,
∴在 中, .
【解析】【分析】(1)根据“∠B=90°,AC⊥CD”得出∠2=∠BAC,即可得出答案;(2)由(1)可得AC=CD,并根据勾股定理求出AC的值,再次利用勾股定理求出AD的值,即可得出答案.
24.【答案】(1)解:如图所示:
(2)解:过点 作 ,垂足为 .
为 的平分线, .
.
在 中, ,
.
【解析】【分析】(1)利用尺规作出角CAB的角平分线即可;
(2)证明 .即可求出 .
25.【答案】(1)解:筝形 的性质: ,
如图,连接PN,
在 和 中,
,
∴ ,
∴
(2)解:四边形 是筝形,
证明:∵ 平分 , , ,
∴ ,
在 和 中,
,
∴ ,
∴ ,
∴四边形 是筝形.
【解析】【分析】(1)连接PN,易证△PQN≌△PMN,然后根据全等三角形的性质进行解答;
(2)由角平分线的性质可得DE=DF,证明△AED≌△AFD,得到AE=AF,据此判断.
26.【答案】(1)115°;80°
(2)解:,理由如下:
如图:
,
,
平分,平分,
,,
,
,
即,
故答案为:;
(3)解:在上取点和,使,,如图:
,是的角平分线,
,,
又,,
≌,≌,
,,,,
,
,
,,
,
,
米,
米,
米,即米
,
米,
答:出水管至少要71米.
【解析】【解答】解:(1)如图:
,即,
,
平分,平分,
,,
,
,
即,
故答案为:;
②若,即,
,
平分,平分,
,,
,
,
即
故答案为:;
【分析】(1)①由内角和定理可得∠ABC+∠ACB=130°,结合角平分线的概念可得∠DBC+∠ECB=(∠ABC+∠ACB)=65°,然后利用内角和定理进行计算;
②由内角和定理得∠OBC+∠OCB=50°,结合角平分线得∠ABC+∠ACB=2(∠OBC+∠OCB)=100°,然后利用内角和定理进行计算;
(2)由三角形的内角和定理可得∠ABC+∠ACB=180°-x,根据角平分线的概念可得∠DBC=∠ABC,∠ECB=∠ACB,则∠DBC+∠ECB=(∠ABC+∠ACB)=90°-x,再利用内角和定理进行解答即可;
(3)在BC上取点G和H,使BG=BE,CH=DC,易得∠EBO=∠GBO,∠DCO=∠HCO,用SAS证明△BEO≌△BGO,△ODC≌△OHC,得到∠BOG=∠BOE,∠HOC=∠DOC,OG=OE,OH=OD,易得∠OBC+∠OCB=30°,则∠BOE=∠DOC=30°,∠BOC=150°,∠BOG=∠HOC=30°,∠GOH=90°,然后利用三角形的面积公式进行计算.
1 / 1
一、单选题
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.下列各组数中能作为直角三角形的三边长的是( )
A.6,7,8 B.5,6,7 C.4.5,6,7.5 D.4,5,6
3.如图,点A,E,F,D在同一直线上,若AB∥CD,AB=CD,AE=FD,则图中的全等三角形有 ( )
A.1对 B.2对 C.3对 D.4对
4.下图所示的五角星是用螺栓将两端打有孔的5根木条连接构成的图形,它的形状不稳定。如果在木条交叉点打孔加装螺栓的办法使其形状稳定,那么至少需要添加( )个螺栓。
A.1 B.2 C.3 D.4 。
5.下列各组数可以是一个三角形的三边长的是( )
A.1,1,2 B.3,4,5 C.5,7,12 D.10,11,22
6.在Rt△ABC中,CD是斜边AB上的中线,则以下判断正确的是( )
A.BC=2CD B.CD=2AB C.AC=2CD D.CD=BD
7.如图,在△ABC中,AC=AB,∠BAC=90°,BD平分∠ABC,与AC相交于点F,CD⊥BD,垂足为D,交BA的延长线于点E,AH⊥BC交BD于点M,交BC于点H,下列选项不正确的是( )
A.∠E=67.5° B.∠AMF=∠AFM
C.BF=2CD D.BD=AB+AF
8.如图,在已知的△ABC中,按以下步骤作图:
①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
A.50° B.45° C.30° D.25°
9.如图,在△ABC中,∠C=90°,AD是△ABC的一条角平分线.若AC=6,AB=10,则点D到AB边的距离为( )
A.2 B.2.5 C.3 D.4
10.如图所示,在等边三角形ABC中,D,E分别在边AB,BC上,且,AE与CD交于点F,,垂足为点G.下列结论:①;②;③是等边三角形;④,其中正确结论的个数是( )
A.3 B.2 C.1 D.0
11.如图,直角△ADB中,∠D=90°,C为AD上一点,且∠ACB的度数为 ,则 的值可能是( )
A.10 B.20 C.30 D.40
二、填空题
12.如图,l1∥l2,则 .
13.如图,五角星的五个顶角分别是,,,,,剪掉,若,则与的度数和为 .
14.已知 中, ,则这个三角形是 三角形.
15.如图,△ABC
中,∠BOC =115°,BD,CE 是∠ABC,∠ACB 的平分线,则∠A的度数 .
16.我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内正六边形的面积S6,则S6= .
三、作图题
17.如图,∠MON及ON上一点A.
求作:点P,使得PA⊥ON,且点P到∠MON两边的距离相等.
四、解答题
18.如图,在△ABC中,边BC=30,点D在边AB上,BD=18,连接CD,CD=24,当AD=CD时,求AC的长.
19.如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=80°,∠ABC=70°.求∠BAD,∠AOF.
20.如图,,垂足分别为.
(1)求证:;
(2)若,求四边形的面积.
21.如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴的对称图形△A1B1C1,写出△ABC关于x轴对称的△A2B2C2的各点坐标.
22.已知,在Rt△ABC中,,,点F是射线CA上一点,连接BF,过点C作CE⊥BF,垂足为点E,直线CE,AB相交于点D。
图1 图2 图3
(1)如图1,当点F在线段CA的延长线上时,求证:;
(2)如图2,当点F在线段CA上时,求证:EA平分∠DEB;
(3)如图3,当点F在线段CA上时,若,△BDE的面积为16,求BE的长。
23.如图,在四边形 中, ,点 是 边上一点, , .
(1)求证: .
(2)若 , ,求 的长.
24.如图,在 中, .
(1)用尺规作出 的平分线,并标出它与边 的交点 (保留作图痕迹,不写作法);
(2)若 , ,求 的长.
25.如图,在四边形 中, , ,我们把这种两组邻边分别相等的四边形叫作筝形.
(1)请你写出筝形 对角线或角的一个性质,并证明.
(2)如图, 是 的角平分线, , ,垂足分别为 , .请判断四边形 是否为筝形,证明你的结论.
26.在中,平分,平分,和交于点,其中令,.
(1)【计算求值】如图,如果,则 ;
如果,则 .
(2)【猜想证明】如图2请你根据(1)中【计算求值】的心得猜想写出与的关系式为 ,并请你说明你的猜想的正确性.
(3)【解决问题】如图3,某校园内有一个如图2所示的三角形的小花园,花园中有两条小路,和为三角形的角平分线,交点为点,在处建有一个自动浇水器,需要在边取一处接水口,经过测量得知,米,米,请你求出水管至少要多长?结果取整数
答案解析部分
1.【答案】A
【解析】【解答】A、不是轴对称图形,故本选项符合题意;
B、是轴对称图形,故本选项不符合题意;
C、是轴对称图形,故本选项不符合题意;
D、是轴对称图形,故本选项不符合题意.
故答案为:A.
【分析】根据轴对称图形的定义逐项判断即可。
2.【答案】C
【解析】【解答】解:A、
,不符合题意;
B、
,不符合题意;
C、
,符合题意;
D、
,不符合题意;
故答案为:C.
【分析】根据勾股定理的逆定理逐项判断即可。
3.【答案】C
【解析】【解答】解:∵AE=DF,
∴AE+EF=DF+EF,
∴AF=DE,
∵AB∥CD,
∴∠A=∠D,
在△BAF和△CDE中,
,
∴△BAF≌△CDE(SAS),
在△BAE和△CDF中,
,
∴△BAE≌△CDF(SAS),
∴BE=CF,∠AEB=∠DFC,
∴∠BEF=∠CFE,
在△BEF和△CFE中,
,
∴△BEF≌△CFE(SAS),
即全等三角形有3对,
故C符合题意.
故答案为:C.
【分析】根据题意可得出AF=DE,∠A=∠D,利用SAS分别得出△BAF≌△CDE和△BAE≌△CDF,再由全等三角形的性质证得∠BEF=∠CFE,利用SAS证得△BEF≌△CFE,从而得到答案.
4.【答案】A
【解析】【解答】解 :
A点加上了螺栓后,根据三角形的稳定性,原不稳定的五角星就具有稳定性了。
故应选 :A.
【分析】根据三角形的稳定性,在A处打上螺栓,五角星的各边就固定了。
5.【答案】B
【解析】【解答】解: A、∵1+1=2 , 不能组成三角形,故A选项不符合题意;
B、 , 能组成三角形,故B选项符合题意;
C、 , 不能组成三角形,故C选项不符合题意;
D、 , 能组成三角形,故D选项不符合题意.
故答案为:B.
【分析】根据三角形三边关系,只需要判断较小两边的和是否大于较大边长即可.
6.【答案】D
【解析】【解答】解:∵CD是斜边AB的中线,
∴AB=2CD,故A、B、C不符合题意;
∴CD=BD,故D符合题意;
故答案为:D.
【分析】利用直角三角形斜边上的中线等于斜边的一半,可得到AB=2CD,CD=BD=AD,由此可得到正确结论的选项.
7.【答案】D
【解析】【解答】解:A、∵AC=AB,∠BAC=90°,∴∠B=45°,∴∠DBE=22.5°,
∴∠E=90°-∠DBE=90°-22.5°=67.5°,正确,不符合题意;
B、∵∠B=45°,∴∠BAH=∠ACB=90°-∠B=45°,∴∠AMF=∠ABM+∠BAM
=22.5°+45°=67.5°,∠AFM=∠ACB+∠CBF=45°+22.5°=67.5°,正确,符合题意;
CD、∵AB=AC,∠BAC=∠EAC=90°,∠AFB=∠CFD,∴∠ABF=∠FCD,∴△ABF≌△ACE(ASA),∴AF=AE,∴AB+AF=AB+AE=BE>BD,D错误,符合题意;∵BD平分∠ABC,BD⊥EC,∴△ABC是等腰三角形,∴ED=CD,∴EC=2CD,∵△ABF≌△ACE,∴BF=EC,∴BF=2CD,∴C正确,不符合题意.
故答案为:D.
【分析】根据等腰三角形的性质,结合三角形外角的性质可求∠E、∠AMF和∠AFM的度数;利用角边角定理可证△ABF≌△ACE,得出对应边相等,再结合直角三角形斜边最大可得BD
【解析】【解答】解:∵根据题意得出MN是线段BC的垂直平分线,
∴CD=BD,即∠B=∠BCD.
∵CD=AC,
∴∠CDA=∠A=50°,
∵∠B+∠BCD=∠CAD,
∴∠B= ∠CDA=25°.
故答案为:D.
【分析】由作图痕迹可知MN是线段BC的垂直平分线,然后利用中垂线的性质和等腰三角形的性质求得∠B=∠BCD,∠CDA=∠A=50°,最后利用三角形外角的性质求解.
9.【答案】C
【解析】【解答】解:作DE⊥AB于E,如图,
在Rt△ABC中,BC= =8,
∵AD是△ABC的一条角平分线,DC⊥AC,DE⊥AB,
∴DE=DC,
设DE=DC=x,
S△ABD= DE AB= AC BD,
即10x=6(8﹣x),解得x=3,
即点D到AB边的距离为3.
故答案为C.
【分析】作DE⊥AB于E,由勾股定理计算出可求BC=8,再利用角平分线的性质得到DE=DC,设DE=DC=x,利用等等面积法列方程、解方程即可解答.
10.【答案】A
【解析】【解答】解:∵等边,
∴,,
∵,
∴,
∴,①正确;
∴,
∴,
在中,
,②正确;
∵,,
∴,
∴不是等腰三角形,③错误;
∵,,
∴,
∴,
∴,④正确,
综上所述,正确的有①②④.
故答案为:A
【分析】先根据等边三角形的性质得到,,进而运用三角形全等的判定与性质证明即可判断①;进而根据题意进行角的运算即可判断②;从而结合等腰三角形的判定即可判断③;再结合题意进行角的运算,运用含30°角的直角三角形的性质即可判断④。
11.【答案】C
【解析】【解答】∠ACB=∠90°+∠CBD
∴(5x 10)°=∠90°+∠CBD
化简得:x=20+ ∠DBC
∵0°<∠DBC<90°
∴20°
【分析】根据三角形的外角性质和三角形内角∠DBC的取值范围得出x的范围。
12.【答案】180°
【解析】【解答】如图:
∵l1∥l2,∴ ,
∵ 是三角形的一个外角,∴ ,
∵ 与 是邻补角,∴ ,
∴ ,即:
∴
故答案为:
【分析】根据两直线平行同位角相等、三角形外角定理以及邻补角的概念列式计算即可;
13.【答案】
【解析】【解答】如图,
∵∠1=∠B+∠D,∠2=∠A+∠C,
∴∠1+∠2=
∵∠1+∠2+
=180°
∴6
=180°
∴=30°
∵∠BMN+∠MNC
=∠4+∠E+∠3+∠E
=180°+∠E
=180°+30°
=210°.
故答案为:
.
【分析】根据三角形外角和性质:∠1+∠2=
,根据三角形内角定理:∠1+∠2+
=180°,求得
,再根据∠BMN+∠MNC=∠4+∠E+∠3+∠E可得。
14.【答案】直角
【解析】【解答】解:设∠A、∠B、∠C分别为α、3α、4α,
则α+3α+4α=180°,
解得α=22.5°,
所以,∠C=4×22.5°=90°,
这个三角形是直角三角形.
故答案为:直角.
【分析】根据比设∠A、∠B、∠C分别为α、3α、4α,然后根据三角形的内角和等于180°列式求出∠C,作出判断即可.
15.【答案】50°
【解析】【解答】解:∵∠BOC =115°,
∴∠OBC+∠OCB=180°-115°=65°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC= ∠ABC,∠OCB= ∠ACB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=130°,
∴∠A=180°-130°=50°,
故答案为:50°.
【分析】利用角平分线的性质得到角的关系,再利用三角形的内角和求解即可。
16.【答案】
【解析】【解答】解:如图所示,
单位圆的半径为1,则其内接正六边形ABCDEF中,
△AOB是边长为1的正三角形,
所以正六边形ABCDEF的面积为
S6=6× ×1×1×sin60°= .
故答案为: .
【分析】根据题意画出图形,结合图形求出单位圆的内接正六边形的面积.
17.【答案】解:如图所示,点P即为所求.
【解析】【分析】过点A作AP⊥ON,交∠MON 的平分线于点P.
18.【答案】解:
为直角三角形,
在中
【解析】【分析】由勾股定理逆定理知△BCD为直角三角形,且∠BDC=90°,由题意可得AD=CD=24,然后在Rt△ADC中,利用勾股定理计算即可.
19.【答案】解:∵AD是高,∠ABC=70°,
∴∠BAD=90°﹣70°=20°,
∵AE、BF是角平分线,∠BAC=80°,∠ABC=70°,
∴∠ABO=35°,∠BAO=40°,
∴∠AOF=∠ABO+∠BAO=75°
【解析】【分析】在直角三角形中,根据两锐角互余即可得到∠BAD=20°,根据角平分线的性质可求出∠BAO和∠ABO,最后由三角形外角的性质求得∠AOF=75°.
20.【答案】(1)证明:在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC(HL);
(2)解:由(1)知:△ABC≌△ADC,
∴BC=CD=3,S△ABC=S△ADC,
∴S△ABC=AB BC=×4×3=6,
∴S△ADC=6,
∴S四边形ABCD=S△ABC+S△ADC=12,
答:四边形ABCD的面积是12.
【解析】【分析】(1)根据三角形全等的判定证明Rt△ABC≌Rt△ADC(HL)即可求解;
(2)根据三角形全等的性质得到BC=CD=3,S△ABC=S△ADC,进而结合题意运用S四边形ABCD=S△ABC+S△ADC即可求解。
21.【答案】解:△ABC的各顶点坐标:A(﹣1,2),B(﹣3,1),C(1,﹣2);
△A1B1C1如图所示:
△ABC关于x轴对称的△A2B2C2的各点坐标:A2(﹣1,-2),B2(﹣3,﹣1),C2(1,2).
【解析】【分析】根据平面直角坐标系写出点A、B、C的坐标即可;
先找出点A、B、C关于y轴的对称点A1、B1、C1的位置,然后顺次连接即可;
根据关于x轴对称的点的横坐标不变,纵坐标互为相反数解答.
22.【答案】(1)证明:∵CE⊥BF,
∴∠CEB=90°,
∴∠CEB=∠BAC=90°,
∴∠ACD+∠CDA=∠ABF+∠EDB.
∵∠CDA=∠EDB,
∴∠ACD=∠ABF.
∵∠ACD=∠ABF,AC=AB,∠CAD=∠BAF,
∴△ACD≌△ABF(ASA),
∴AF=AD,
∴CF=AC+AF=AC+AD=AB+AD.
(2)证明:过A作AM⊥CD于点M,AN⊥BE于点N,则∠CMA=∠ANB=90°.
∵∠CEF=∠CAB=90°,∠CFE=∠BFA,
∴∠MCA=∠NBA.
∵∠MCA=∠NBA,∠CMA=∠ANB,AC=AB,
∴△ACM≌△ABN(AAS),
∴AM=AN,
∴EA平分∠DEB.
(3)解:∵ ∠CEB=∠CAB=90°,∠CFE=∠AFB,
∴△ECF=∠FBA.
∵∠CAD=∠BED=90°,AC=BC,∠DCA=∠FBA,
∴△ABF≌△ACD(ASA),
∴AF=AD.
∵CF=CA,
∴CF=AF=AD=AC=AB.
过E作EG⊥BD于点G,
∵S△ABE=AB·EG,S△ADE=AD·EG,
∴S△ABE=2S△ADE.
∵S△BDE=16,
∴S△ABE=,S△ADE=.
过A作AM⊥CD于点M,AN⊥BE于点N,
∴S△ADE=AM·DE,S△ABE=AN·BE.
由(2)得AM=AN,
∴BE=2DE.
设DE=x,则BE=2x.
∵S△BDE=16,
∴DE·BE=16,
∴x·2x=16,
∴x=4,
∴BE=8.
【解析】【分析】(1)由垂直的定义可得∠CEB=∠BAC=90°,由等角的余角相等可得∠ACD=∠ABF,利用ASA证明△ACD≌△ABF,得到AF=AD,据此解答;
(2)过A作AM⊥CD于点M,AN⊥BE于点N,则∠CMA=∠ANB=90°,同理证明△ACM≌△ABN,得到AM=AN,据此证明;
(3)利用ASA证明△ABF≌△ACD,得到AF=AD,结合已知条件可得CF=AF=AD=AC=AB,过E作EG⊥BD于点G,由三角形的面积公式可得S△ABE=2S△ADE,进而推出BE=2DE,设DE=x,则BE=2x,根据S△BDE=DE·BE=16可得x的值,进而可求出BE的长.
23.【答案】(1)证明:∵ ,
∴ .
∵ ,
∴ ,
∴ .
在 和 中,
.
(2)解:∵ ,
∴ , .
∵ ,
∴在 中, ,
∵ ,
∴在 中, .
【解析】【分析】(1)根据“∠B=90°,AC⊥CD”得出∠2=∠BAC,即可得出答案;(2)由(1)可得AC=CD,并根据勾股定理求出AC的值,再次利用勾股定理求出AD的值,即可得出答案.
24.【答案】(1)解:如图所示:
(2)解:过点 作 ,垂足为 .
为 的平分线, .
.
在 中, ,
.
【解析】【分析】(1)利用尺规作出角CAB的角平分线即可;
(2)证明 .即可求出 .
25.【答案】(1)解:筝形 的性质: ,
如图,连接PN,
在 和 中,
,
∴ ,
∴
(2)解:四边形 是筝形,
证明:∵ 平分 , , ,
∴ ,
在 和 中,
,
∴ ,
∴ ,
∴四边形 是筝形.
【解析】【分析】(1)连接PN,易证△PQN≌△PMN,然后根据全等三角形的性质进行解答;
(2)由角平分线的性质可得DE=DF,证明△AED≌△AFD,得到AE=AF,据此判断.
26.【答案】(1)115°;80°
(2)解:,理由如下:
如图:
,
,
平分,平分,
,,
,
,
即,
故答案为:;
(3)解:在上取点和,使,,如图:
,是的角平分线,
,,
又,,
≌,≌,
,,,,
,
,
,,
,
,
米,
米,
米,即米
,
米,
答:出水管至少要71米.
【解析】【解答】解:(1)如图:
,即,
,
平分,平分,
,,
,
,
即,
故答案为:;
②若,即,
,
平分,平分,
,,
,
,
即
故答案为:;
【分析】(1)①由内角和定理可得∠ABC+∠ACB=130°,结合角平分线的概念可得∠DBC+∠ECB=(∠ABC+∠ACB)=65°,然后利用内角和定理进行计算;
②由内角和定理得∠OBC+∠OCB=50°,结合角平分线得∠ABC+∠ACB=2(∠OBC+∠OCB)=100°,然后利用内角和定理进行计算;
(2)由三角形的内角和定理可得∠ABC+∠ACB=180°-x,根据角平分线的概念可得∠DBC=∠ABC,∠ECB=∠ACB,则∠DBC+∠ECB=(∠ABC+∠ACB)=90°-x,再利用内角和定理进行解答即可;
(3)在BC上取点G和H,使BG=BE,CH=DC,易得∠EBO=∠GBO,∠DCO=∠HCO,用SAS证明△BEO≌△BGO,△ODC≌△OHC,得到∠BOG=∠BOE,∠HOC=∠DOC,OG=OE,OH=OD,易得∠OBC+∠OCB=30°,则∠BOE=∠DOC=30°,∠BOC=150°,∠BOG=∠HOC=30°,∠GOH=90°,然后利用三角形的面积公式进行计算.
1 / 1
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
