京改版九年级数学上册第十八章相似形单元复习题(含解析)
文档属性
| 名称 | 京改版九年级数学上册第十八章相似形单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 519.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览



文档简介
京改版九年级数学上册第十八章相似形单元复习题
一、单选题
1.如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD︰AB=3︰4,AE=6,则AC等于( )
A.3 B.4 C.6 D.8
2.已知 ,那么 ( ).
A. B. C. D.
3.如图,,则的长为( )
A.4 B.3 C.2.5 D.2
4.小明按照以下步骤画线段AB的三等分点:
画法 图形
1.以A为端点画一条射线; 2.用圆规在射线上依次截取3条等长线段AC、CD、DE,连接BE; 3.过点C、D分别画BE的平行线,交线段AB于点M、N,M、N就是线段AB的三等分点.
这一画图过程体现的数学依据是( )
A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例
5.如图,在△ABC中,DE∥BC,AD=4,AE=3,CE=6,那么BD的值是( )
A.4 B.6 C.8 D.12
6.如图,在△ABC中,点D,E分别是AB,C的中点,则S△ADE:S△ABC=( )
A.1:2 B.1:3 C.1:4 D.1:5
7.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S△ABC=2S△ABF.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
8.如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,若EF:AF=2:5,则S△DEF:S四边形EFBC为( )
A.2:5 B.4:25 C.4:31 D.4:35
9.如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
A.18 B. C. D.
10.如图,在2×2的正方形网格中有9个格点,已经取定点A,B,C,在余下的6个点中任取一点P,满足△ABP与△ABC相似的概率是( )
A. B. C. D.
二、填空题
11.如果点P是线段AB的黄金分割点(AP>BP),那么 的值是 .
12.在比例尺为1:400000的地图上,量得线段AB两地距离是24cm,则AB两地实际距离为 km.
13.若线段a=3 cm,b=12 cm,则a、b的比例中项c= cm.
14.如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=2,AD=1,则DB=
15.工人师傅在修茸一人字架屋顶BAC时需要加固,计划焊接三根钢条AD,DE,FG.在如图所示的△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E,F,G分别是AB,BD,AC上的点,连接DE,GF,交于点H,GF与AD交于点M,当H为FM的中点,BF∶CF=1∶5,AG:AE=5:7时,△AGM的面积为 .
三、解答题
16.已知:如图,AE2=AD·AB,且∠ABE=∠ACB,求证:DE∥BC.
17.如图,若 , 和 相交于点 ,和 相交于点 , , , ,求 .
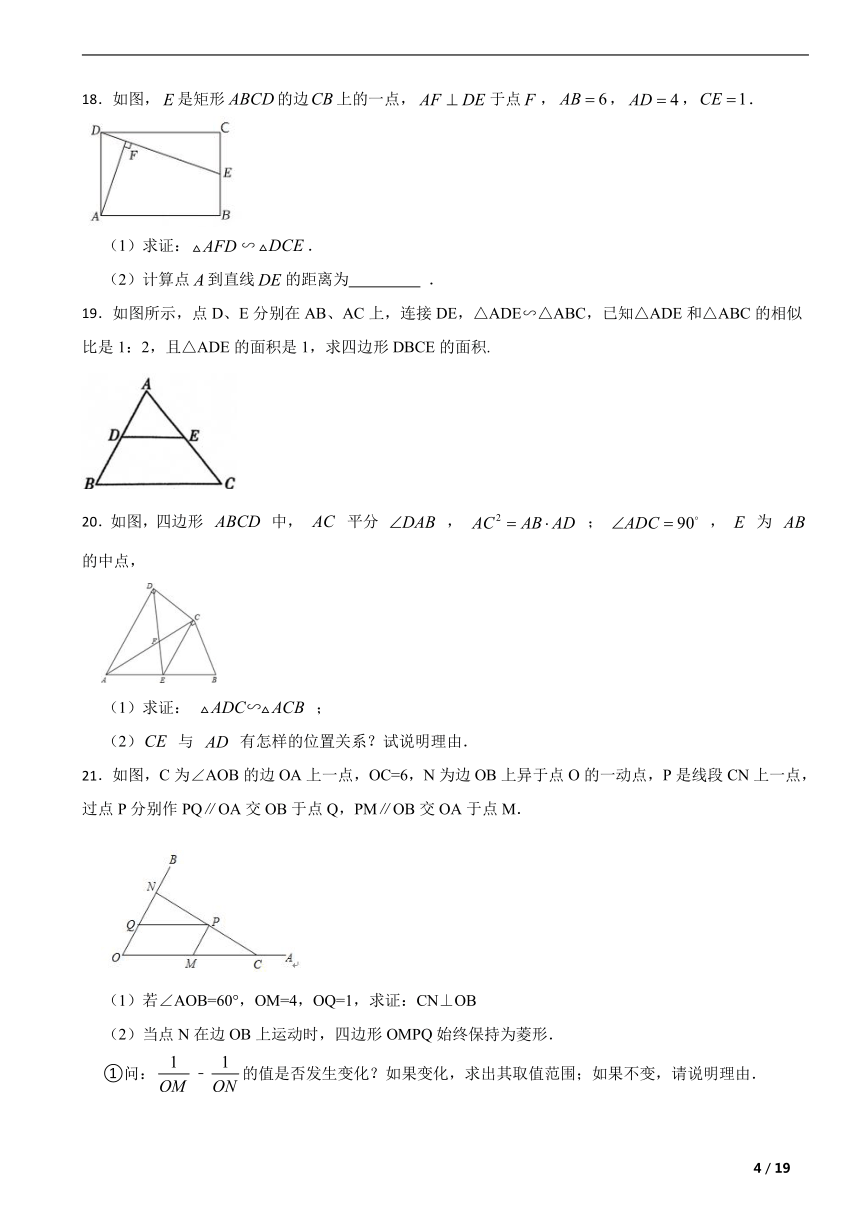
18.如图,是矩形的边上的一点,于点,,,.
(1)求证:∽.
(2)计算点到直线的距离为 .
19.如图所示,点D、E分别在AB、AC上,连接DE,△ADE∽△ABC,已知△ADE和△ABC的相似比是1:2,且△ADE的面积是1,求四边形DBCE的面积.
20.如图,四边形 中, 平分 , ; , 为 的中点,
(1)求证: ;
(2) 与 有怎样的位置关系?试说明理由.
21.如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60°,OM=4,OQ=1,求证:CN⊥OB
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问:﹣的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
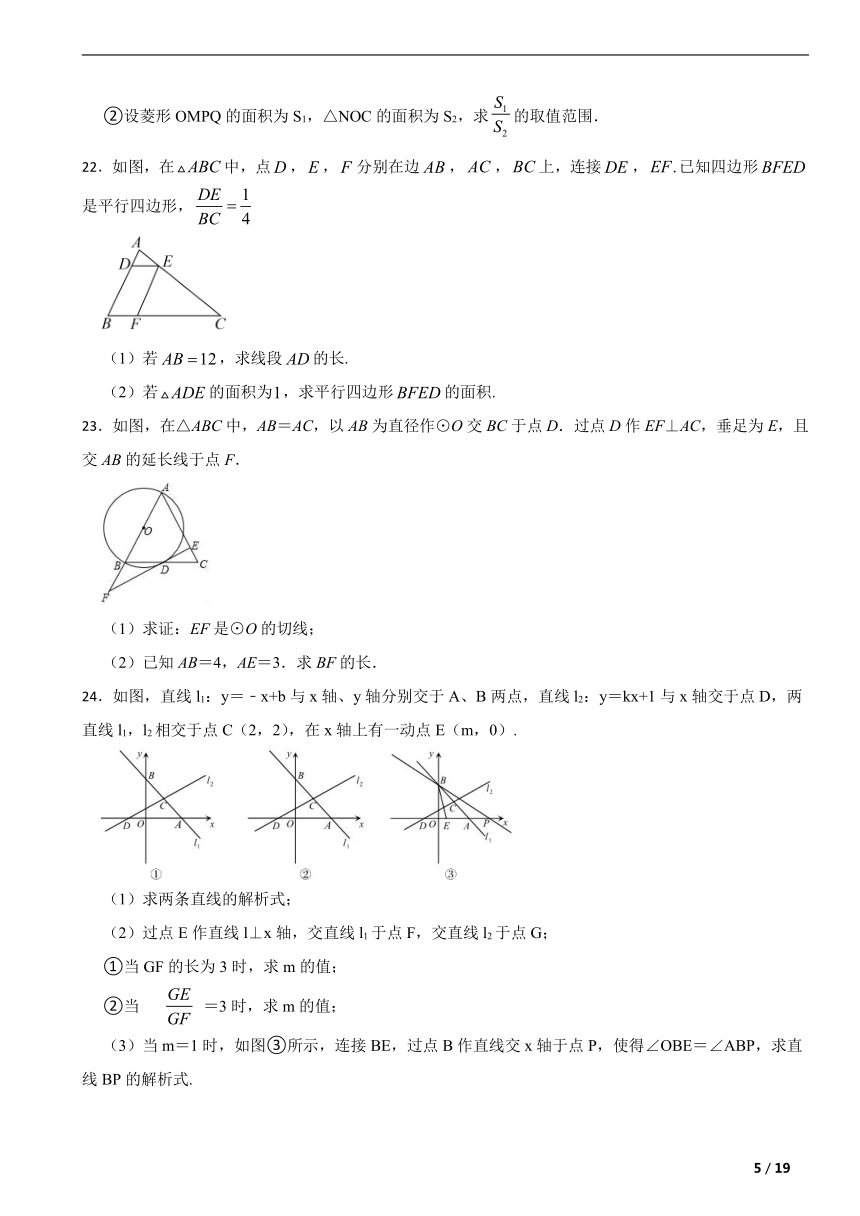
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求的取值范围.
22.如图,在中,点,,分别在边,,上,连接,已知四边形是平行四边形,
(1)若,求线段的长.
(2)若的面积为,求平行四边形的面积.
23.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)已知AB=4,AE=3.求BF的长.
24.如图,直线l1:y=﹣x+b与x轴、y轴分别交于A、B两点,直线l2:y=kx+1与x轴交于点D,两直线l1,l2相交于点C(2,2),在x轴上有一动点E(m,0).
(1)求两条直线的解析式;
(2)过点E作直线l⊥x轴,交直线l1于点F,交直线l2于点G;
①当GF的长为3时,求m的值;
②当
=3时,求m的值;
(3)当m=1时,如图③所示,连接BE,过点B作直线交x轴于点P,使得∠OBE=∠ABP,求直线BP的解析式.
答案解析部分
1.【答案】D
【解析】【解答】∵DE∥BC,∴,即,∴AC=8.
故答案为:D.
【分析】根据平行线分线段成比例进行解答即可.
2.【答案】A
【解析】【解答】 ,
∴可设 ,
.
故答案为:A.
【分析】由比例的性质可设a=2k,b=3k,代入所求代数式计算即可求解.
3.【答案】B
【解析】【解答】解:,
,即,
.
故答案为:B.
【分析】根据平行线分线段成比例定理进行解答即可.
4.【答案】D
【解析】【解答】解:∵CM∥DN∥BE,
∴AC∶CD∶DE=AM∶MN∶BN,
∵AC=CD=DE,
∴AM=MN=NB,
∴这一画图过程体现的数学依据是: 两条直线被一组平行线所截,所得的对应线段成比例.
故答案为:D.
【分析】根据两条直线被一组平行线所截,所得的对应线段成比例 ,即可作答.
5.【答案】C
【解析】【解答】∵DE∥BC,
∴ ,
∵AD=4,AE=3,CE=6,
∴ ,
∴BD=8,
故答案为:C.
【分析】根据平行线分线段成比例得,然后利用比例性质即可求出BD的长。
6.【答案】C
【解析】【解答】解:∵点D、E分别是AB、C的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE= BC,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=( )2= ;
故选:C.
【分析】证出DE是△ABC的中位线,由三角形中位线定理得出DE∥BC,DE= BC,证出△ADE∽△ABC,由相似三角形的面积比等于相似比的平方即可得出结论.
7.【答案】B
【解析】【解答】解:如图,过D作DM∥BE交AC于N,交BC于M,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∴∠EAC=∠ACB,
∵BE⊥AC于点F,
∴∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴ = ,
∵AE= AD= BC,
∴ = ,
∴CF=2AF,故②正确;
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE= BC,
∴BM=CM,CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DN垂直平分CF,
∴DF=DC,故③正确;
∵CF=2AF,
∴S△ABC=3S△ABF.
∴④不正确;
其中正确的结论有3个,
故选:B.
【分析】①根据四边形ABCD是矩形,BE⊥AC,可得∠ABC=∠AFB=90°,又∠BAF=∠CAB,于是△AEF∽△CAB,故①正确;
②根据点E是AD边的中点,以及AD∥BC,得出△AEF∽△CBF,根据相似三角形对应边成比例,可得CF=2AF,故②正确;
③过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE= BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故③正确;
④根据CF=2AF,即可得出结论④错误;即可得出结论.
8.【答案】C
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴CD∥AB,
∴△DEF∽△BAF,
∴==,
∴=()2=,==
设S△DEF=S,则S△ABF=S,S△ADF=S,
∴S△ABD=S△ADF+S△ABF=S+S=S,
∵四边形ABCD为平行四边形,
∴S△ABD=S△DBC=S,
∴S四边形EFBC=S△BDC﹣S△DEF=S﹣S=S,
∴S△DEF:S四边形EFBC=4:31.
故选C.
【分析】由平行四边形的性质可证明△DEF∽△BAF,可求得△DEF和△AFE、△ABF的面积之间的关系,从而可求得△DEF和△BCD的面积之间的关系,可求得答案.
9.【答案】B
【解析】【解答】∵四边形ABCD是正方形,
即 解得:
即 解得:
故答案为:B.
【分析】利用正方形的性质及已知求出MC的长,可证∠B=∠C,∠BAM=∠CMG,利用有两组角对应相等的两三角形相似,可证得△AMB∽△MCG,利用相似三角形的性质,得出对应边成比例,求出CG,DG,再根据AE∥BC证明△MCG∽△EDG,得出对应边成比例,从而可求出DE的长。
10.【答案】A
【解析】【解答】解:满足△ABP与△ABC相似的点有3个,
所以满足△ABP与△ABC相似的概率是 .
故选A.
【分析】找到可以使△ABP与△ABC相似的点,根据概率公式解答即可.
11.【答案】
【解析】【解答】解:∵点P是线段AB的黄金分割点(AP>BP),
∴
故答案为:
【分析】根据黄金分割的定义可知, 黄金比即值为 .
12.【答案】96
【解析】【解答】设AB两地实际距离为
根据题意得:
解得: (cm)
∴AB两地实际距离为
故填:96.
【分析】先设AB两地实际距离为 ,根据比例尺的性质列出方程求解即可.
13.【答案】6
【解析】【解答】由c是线段a,b的比例中项可得:c2=ab=12×3=36,因为c>0,所以c=6cm.故答案为6cm.
【分析】根据c是线段a,b的比例中项,可得c2=ab,把a=3,b=12代入计算,求出c的值,即可求解.
14.【答案】3
【解析】【解答】∵∠ACD=∠ABC,∠A=∠A,
∴△ABC∽△ACD,
∴,
∵AC=2,AD=1,
∴ ,
解得DB=3.
【分析】由题意,在△ABC中,点D在边AB上,满足∠ACD=∠ABC,可证△ABC∽△ACD,再根据相似三角形对应边成比例来解答.
15.【答案】
【解析】【解答】解:过点G作GN∥BC交AD于点N,
∵AB=AC,AD⊥BC,
∴NG∥BC,NG⊥AD,
∴∠B=∠C,BD=DC=6,∠ADF=90°,∠EAD=∠MAG,
∴;
∵BF:CF=1:5,BC=12,
∴BF+CF=12,
解之:BF=2,CF=10,
在Rt△MDF中,点H是MF的中点,
∴DH=HF=MH,
∴∠BDE=∠CFG,∠ADE=∠FMD=∠AMG,
∵∠BDE=∠CFG,∠B=∠C,
∴△BDE∽△CFG,
∴,
∵∠EAD=∠MAG,∠AMG=∠ADE,
∴△ADE∽△AMG,
∴;
解得:,
设AG=5m,则AE=7m,
∴BE=AB-AE=10-7m,CG=AC-AG=10-5m,
∴,
解得:m=1,
经检验,m=1符合题意,
∴AG=5,
∵NG∥BC,
∴△ANG∽△ADC,
∴ , 即
解之:NG=3.
∴.
故答案为:.
【分析】过点G作GN∥BC交AD于点N,则∠B=∠C,BD=DC=6,∠ADF=90°,∠EAD=∠MAG,利用勾股定理可得AD,由BF:CF=1:5结合BC的值可得BF=2,CF=10,由直角三角形斜边上中线的性质可得DH=HF=MH,结合等腰三角形的性质可得∠BDE=∠CFG,∠ADE=∠FMD=∠AMG,证明△BDE∽△CFG,△ADE∽△AMG,设AG=5m,则AE=7m,BE=10-7m,CG=10-5m,根据相似三角形的性质可得m的值,证明△ANG∽△ADC,根据相似三角形的性质可得NG,然后根据三角形的面积公式进行计算.
16.【答案】证明:∵ ,
∴ ,
∵∠A=∠A(公共角),
∴ ∽ ,
∴∠AED=∠ABE,
又∵∠ABE=∠ACB,
∴∠AED=∠ACB,
∴DE∥BC.
【解析】【分析】先证明 ∽ ,再利用相似三角形的性质及已知条件可证明∠AED=∠ACB,从而证明结论.
17.【答案】解:∵ ,
∴ ,
∴ ,
解得
【解析】【分析】根据相似三角形的面积的比等于相似比的平方可求解。
18.【答案】(1)证明:四边形是矩形,
,,,
,
,
,
,
,
∽,
(2)
【解析】【解答】解:(2)∵矩形ABCD,,
∴DC=AB=6,
在Rt△CDE中,由勾股定理可得:,
∵∽,
∴,
∴,
∴,
故答案为:.
【分析】(1)利用角的运算和等量代换可得,再结合,即可得到∽;
(2)先利用勾股定理求出DE的长,再利用相似三角形的性质可得,再将数据代入求出AF的长即可.
19.【答案】解:∵△ADE和△ABC的相似比是1:2,
又∵△ADE的面积是1,
∴S四边形
【解析】【分析】利用相似三角形的面积比等于相似比的平方,利用△ADE的面积,可求出△ABC的面积,再利用四边形DBCE的面积等于△ABC的面积减去△ADE的面积,代入计算可求出结果.
20.【答案】(1)解:∵ 平分 ,
∴ ,
∵ ,
∴ .
(2)解: ;
∵ 是 的中点,
∴ ,
∴ .
∵ 平分 ,
∴ ,
∴ ,
∴ .
【解析】【分析】(1)证明∠DAC=∠CAB,∠ADC=∠ACB=90°,即可解决问题;(2)根据直角三角形的性质,可得CE与AE的关系,根据等腰三角形的性质,可得∠EAC=∠ECA,根据角平分线的定义,可得∠CAD=∠CAB,根据平行线的判定,可得答案.
21.【答案】(1)解:(1)过P作PE⊥OA于E,
∵PQ∥OA,PM∥OB,
∴四边形OMPQ为平行四边形,
∴PM=OQ=1,∠PME=∠AOB=60°,
∴PE=PM sin60°=,ME=,
∴CE=OC﹣OM﹣ME=,
∴tan∠PCE==,
∴∠PCE=30°,
∴∠CPM=90°,
又∵PM∥OB,
∴∠CNO=∠CPM=90°,
则CN⊥OB
(2)解:①﹣的值不发生变化,理由如下:设OM=x,ON=y,∵四边形OMPQ为菱形,∴OQ=QP=OM=x,NQ=y﹣x,∵PQ∥OA,∴∠NQP=∠O,又∵∠QNP=∠ONC,∴△NQP∽△NOC,∴=,即=,
∴6y﹣6x=xy.两边都除以6xy,得﹣=,即﹣=.
②过P作PE⊥OA于E,过N作NF⊥OA于F,则S1=OM PE,S2=OC NF,∴=.∵PM∥OB,∴∠PMC=∠O,又∵∠PCM=∠NCO,∴△CPM∽△CNO,∴==,∴==﹣(x﹣3)2+,∵0<x<6,则根据二次函数的图象可知,0<≤.
【解析】【分析】(1)过P作PE⊥OA于E,利用两组对边平行的四边形为平行四边形得到OMPQ为平行四边形,利用平行四边形的对边相等,对角相等得到PM=OQ=1,∠PME=∠AOB=60°,进而求出PE与ME的长,得到CE的长,求出tan∠PCE的值,利用特殊角的三角函数值求出∠PCE的度数,得到PM于NC垂直,而PM与ON平行,即可得到CN与OB垂直;
(2)﹣的值不发生变化,理由如下:设OM=x,ON=y,根据OMPQ为菱形,得到PM=PQ=OQ=x,QN=y﹣x,根据平行得到三角形NQP与三角形NOC相似,由相似得比例即可确定出所求式子的值;
②过P作PE⊥OA于E,过N作NF⊥OA于F,表示出菱形OMPQ的面积为S1,△NOC的面积为S2,得到,由PM与OB平行,得到三角形CPM与三角形CNO相似,由相似得比例求出所求式子 的范围即可.
22.【答案】(1)解:四边形是平行四边形,
,
,
,
,
,
;
(2)解:∽,
,
的面积为,
的面积是,
四边形是平行四边形,
,
,
,
的面积,
平行四边形的面积.
【解析】【分析】(1)根据平行四边形的性质可得DE∥BF,证明△ADE∽△ABC,然后根据相似三角形的对应边成比例进行计算;
(2)根据相似三角形的面积比等于相似比的平方可得 ,则△ABC的面积是16,由平行四边形的性质可得EF∥AB,证明△EFC∽△ABC,根据相似三角形的面积比等于相似比的平方可得△EFC的面积,据此求解.
23.【答案】(1)证明:连接OD,AD, ∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴BD=CD, ∵OA=OB,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)解:∵OD∥AE, ∴△ODF∽△AEF, ∴ ,
∵AB=4,AE=3,
∴ , ∴BF=2.
【解析】【分析】(1)作辅助线,根据等腰三角形三线合一得BD=CD,根据三角形的中位线可得OD∥AC,所以得OD⊥EF,从而得结论;(2)证明△ODF∽△AEF,列比例式可得结论.
24.【答案】(1)解:将点C(2,2)代入直线l1:y=﹣x+b中,得-2+b=2,
解得b=4,
∴直线l1:y=﹣x+4;
将点C(2,2)代入直线l2:y=kx+1中,得2k+1=2,
解得k= ,
∴直线l2:y= x+1;
(2)解:①∵l⊥x轴,E(m,0).
∴点F( ),G( ),
当m<2时, ,解得m=0;
当m>2时, ,解得m=4;
∴当GF的长为3时,m的值为0或4;
.
②∵ =3,
∴GE=3GF,
当m<2时, ,解得 ;
当m>2时, ,解得 ;
∴ 或 ;
(3)解:过点P作PH⊥AB于H,
∵y=﹣x+4,
∴A(4,0),B(0,4),
∴OA=OB=4,
∴∠BAO=∠ABO= , ,
∴∠HAP=∠HPA= ,
∴AH=PH,
设PH=a,
∵∠OBE=∠ABP,∠BOE=∠BHP= ,
∴△BHP∽△BOE,
∴ ,
∴ ,
解得 ,
∴ ,
∴P( ),
设直线BP的解析式为y=nk+b,
∴ ,解得 ,
∴ .
.
【解析】【分析】(1)将C(2,2)代入y=-x+b中可得b的值,进而可得直线l1的解析式,将C(2,2)代入y=kx+1中求出k的值,进而可得直线l2的解析式;
(2)①易得F(m,-m+4),G(m,
m+1),表示出GF,然后根据GF=3求解即可;
②由已知条件可得GE=3GF,然后分别表示出GE、GF,根据GE=3GF求解即可;
(3)过点P作PH⊥AB于点H,易得A(4,0),B(0,4),则OA=OB=4,利用勾股定理求出AB,设PH=a,证明△BHP∽△BOE,根据相似三角形的性质求出a,进而可得AP,求出点P的坐标,设直线BP的解析式为y=kx+b,然后将点B、P的坐标代入求出k、b,据此可得直线BP的解析式.
1 / 1
一、单选题
1.如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD︰AB=3︰4,AE=6,则AC等于( )
A.3 B.4 C.6 D.8
2.已知 ,那么 ( ).
A. B. C. D.
3.如图,,则的长为( )
A.4 B.3 C.2.5 D.2
4.小明按照以下步骤画线段AB的三等分点:
画法 图形
1.以A为端点画一条射线; 2.用圆规在射线上依次截取3条等长线段AC、CD、DE,连接BE; 3.过点C、D分别画BE的平行线,交线段AB于点M、N,M、N就是线段AB的三等分点.
这一画图过程体现的数学依据是( )
A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例
5.如图,在△ABC中,DE∥BC,AD=4,AE=3,CE=6,那么BD的值是( )
A.4 B.6 C.8 D.12
6.如图,在△ABC中,点D,E分别是AB,C的中点,则S△ADE:S△ABC=( )
A.1:2 B.1:3 C.1:4 D.1:5
7.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S△ABC=2S△ABF.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
8.如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,若EF:AF=2:5,则S△DEF:S四边形EFBC为( )
A.2:5 B.4:25 C.4:31 D.4:35
9.如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
A.18 B. C. D.
10.如图,在2×2的正方形网格中有9个格点,已经取定点A,B,C,在余下的6个点中任取一点P,满足△ABP与△ABC相似的概率是( )
A. B. C. D.
二、填空题
11.如果点P是线段AB的黄金分割点(AP>BP),那么 的值是 .
12.在比例尺为1:400000的地图上,量得线段AB两地距离是24cm,则AB两地实际距离为 km.
13.若线段a=3 cm,b=12 cm,则a、b的比例中项c= cm.
14.如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=2,AD=1,则DB=
15.工人师傅在修茸一人字架屋顶BAC时需要加固,计划焊接三根钢条AD,DE,FG.在如图所示的△ABC中,AB=AC=10,BC=12,AD⊥BC于点D,点E,F,G分别是AB,BD,AC上的点,连接DE,GF,交于点H,GF与AD交于点M,当H为FM的中点,BF∶CF=1∶5,AG:AE=5:7时,△AGM的面积为 .
三、解答题
16.已知:如图,AE2=AD·AB,且∠ABE=∠ACB,求证:DE∥BC.
17.如图,若 , 和 相交于点 ,和 相交于点 , , , ,求 .
18.如图,是矩形的边上的一点,于点,,,.
(1)求证:∽.
(2)计算点到直线的距离为 .
19.如图所示,点D、E分别在AB、AC上,连接DE,△ADE∽△ABC,已知△ADE和△ABC的相似比是1:2,且△ADE的面积是1,求四边形DBCE的面积.
20.如图,四边形 中, 平分 , ; , 为 的中点,
(1)求证: ;
(2) 与 有怎样的位置关系?试说明理由.
21.如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60°,OM=4,OQ=1,求证:CN⊥OB
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问:﹣的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求的取值范围.
22.如图,在中,点,,分别在边,,上,连接,已知四边形是平行四边形,
(1)若,求线段的长.
(2)若的面积为,求平行四边形的面积.
23.如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)已知AB=4,AE=3.求BF的长.
24.如图,直线l1:y=﹣x+b与x轴、y轴分别交于A、B两点,直线l2:y=kx+1与x轴交于点D,两直线l1,l2相交于点C(2,2),在x轴上有一动点E(m,0).
(1)求两条直线的解析式;
(2)过点E作直线l⊥x轴,交直线l1于点F,交直线l2于点G;
①当GF的长为3时,求m的值;
②当
=3时,求m的值;
(3)当m=1时,如图③所示,连接BE,过点B作直线交x轴于点P,使得∠OBE=∠ABP,求直线BP的解析式.
答案解析部分
1.【答案】D
【解析】【解答】∵DE∥BC,∴,即,∴AC=8.
故答案为:D.
【分析】根据平行线分线段成比例进行解答即可.
2.【答案】A
【解析】【解答】 ,
∴可设 ,
.
故答案为:A.
【分析】由比例的性质可设a=2k,b=3k,代入所求代数式计算即可求解.
3.【答案】B
【解析】【解答】解:,
,即,
.
故答案为:B.
【分析】根据平行线分线段成比例定理进行解答即可.
4.【答案】D
【解析】【解答】解:∵CM∥DN∥BE,
∴AC∶CD∶DE=AM∶MN∶BN,
∵AC=CD=DE,
∴AM=MN=NB,
∴这一画图过程体现的数学依据是: 两条直线被一组平行线所截,所得的对应线段成比例.
故答案为:D.
【分析】根据两条直线被一组平行线所截,所得的对应线段成比例 ,即可作答.
5.【答案】C
【解析】【解答】∵DE∥BC,
∴ ,
∵AD=4,AE=3,CE=6,
∴ ,
∴BD=8,
故答案为:C.
【分析】根据平行线分线段成比例得,然后利用比例性质即可求出BD的长。
6.【答案】C
【解析】【解答】解:∵点D、E分别是AB、C的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE= BC,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=( )2= ;
故选:C.
【分析】证出DE是△ABC的中位线,由三角形中位线定理得出DE∥BC,DE= BC,证出△ADE∽△ABC,由相似三角形的面积比等于相似比的平方即可得出结论.
7.【答案】B
【解析】【解答】解:如图,过D作DM∥BE交AC于N,交BC于M,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∴∠EAC=∠ACB,
∵BE⊥AC于点F,
∴∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴ = ,
∵AE= AD= BC,
∴ = ,
∴CF=2AF,故②正确;
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE= BC,
∴BM=CM,CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DN垂直平分CF,
∴DF=DC,故③正确;
∵CF=2AF,
∴S△ABC=3S△ABF.
∴④不正确;
其中正确的结论有3个,
故选:B.
【分析】①根据四边形ABCD是矩形,BE⊥AC,可得∠ABC=∠AFB=90°,又∠BAF=∠CAB,于是△AEF∽△CAB,故①正确;
②根据点E是AD边的中点,以及AD∥BC,得出△AEF∽△CBF,根据相似三角形对应边成比例,可得CF=2AF,故②正确;
③过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE= BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故③正确;
④根据CF=2AF,即可得出结论④错误;即可得出结论.
8.【答案】C
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴CD∥AB,
∴△DEF∽△BAF,
∴==,
∴=()2=,==
设S△DEF=S,则S△ABF=S,S△ADF=S,
∴S△ABD=S△ADF+S△ABF=S+S=S,
∵四边形ABCD为平行四边形,
∴S△ABD=S△DBC=S,
∴S四边形EFBC=S△BDC﹣S△DEF=S﹣S=S,
∴S△DEF:S四边形EFBC=4:31.
故选C.
【分析】由平行四边形的性质可证明△DEF∽△BAF,可求得△DEF和△AFE、△ABF的面积之间的关系,从而可求得△DEF和△BCD的面积之间的关系,可求得答案.
9.【答案】B
【解析】【解答】∵四边形ABCD是正方形,
即 解得:
即 解得:
故答案为:B.
【分析】利用正方形的性质及已知求出MC的长,可证∠B=∠C,∠BAM=∠CMG,利用有两组角对应相等的两三角形相似,可证得△AMB∽△MCG,利用相似三角形的性质,得出对应边成比例,求出CG,DG,再根据AE∥BC证明△MCG∽△EDG,得出对应边成比例,从而可求出DE的长。
10.【答案】A
【解析】【解答】解:满足△ABP与△ABC相似的点有3个,
所以满足△ABP与△ABC相似的概率是 .
故选A.
【分析】找到可以使△ABP与△ABC相似的点,根据概率公式解答即可.
11.【答案】
【解析】【解答】解:∵点P是线段AB的黄金分割点(AP>BP),
∴
故答案为:
【分析】根据黄金分割的定义可知, 黄金比即值为 .
12.【答案】96
【解析】【解答】设AB两地实际距离为
根据题意得:
解得: (cm)
∴AB两地实际距离为
故填:96.
【分析】先设AB两地实际距离为 ,根据比例尺的性质列出方程求解即可.
13.【答案】6
【解析】【解答】由c是线段a,b的比例中项可得:c2=ab=12×3=36,因为c>0,所以c=6cm.故答案为6cm.
【分析】根据c是线段a,b的比例中项,可得c2=ab,把a=3,b=12代入计算,求出c的值,即可求解.
14.【答案】3
【解析】【解答】∵∠ACD=∠ABC,∠A=∠A,
∴△ABC∽△ACD,
∴,
∵AC=2,AD=1,
∴ ,
解得DB=3.
【分析】由题意,在△ABC中,点D在边AB上,满足∠ACD=∠ABC,可证△ABC∽△ACD,再根据相似三角形对应边成比例来解答.
15.【答案】
【解析】【解答】解:过点G作GN∥BC交AD于点N,
∵AB=AC,AD⊥BC,
∴NG∥BC,NG⊥AD,
∴∠B=∠C,BD=DC=6,∠ADF=90°,∠EAD=∠MAG,
∴;
∵BF:CF=1:5,BC=12,
∴BF+CF=12,
解之:BF=2,CF=10,
在Rt△MDF中,点H是MF的中点,
∴DH=HF=MH,
∴∠BDE=∠CFG,∠ADE=∠FMD=∠AMG,
∵∠BDE=∠CFG,∠B=∠C,
∴△BDE∽△CFG,
∴,
∵∠EAD=∠MAG,∠AMG=∠ADE,
∴△ADE∽△AMG,
∴;
解得:,
设AG=5m,则AE=7m,
∴BE=AB-AE=10-7m,CG=AC-AG=10-5m,
∴,
解得:m=1,
经检验,m=1符合题意,
∴AG=5,
∵NG∥BC,
∴△ANG∽△ADC,
∴ , 即
解之:NG=3.
∴.
故答案为:.
【分析】过点G作GN∥BC交AD于点N,则∠B=∠C,BD=DC=6,∠ADF=90°,∠EAD=∠MAG,利用勾股定理可得AD,由BF:CF=1:5结合BC的值可得BF=2,CF=10,由直角三角形斜边上中线的性质可得DH=HF=MH,结合等腰三角形的性质可得∠BDE=∠CFG,∠ADE=∠FMD=∠AMG,证明△BDE∽△CFG,△ADE∽△AMG,设AG=5m,则AE=7m,BE=10-7m,CG=10-5m,根据相似三角形的性质可得m的值,证明△ANG∽△ADC,根据相似三角形的性质可得NG,然后根据三角形的面积公式进行计算.
16.【答案】证明:∵ ,
∴ ,
∵∠A=∠A(公共角),
∴ ∽ ,
∴∠AED=∠ABE,
又∵∠ABE=∠ACB,
∴∠AED=∠ACB,
∴DE∥BC.
【解析】【分析】先证明 ∽ ,再利用相似三角形的性质及已知条件可证明∠AED=∠ACB,从而证明结论.
17.【答案】解:∵ ,
∴ ,
∴ ,
解得
【解析】【分析】根据相似三角形的面积的比等于相似比的平方可求解。
18.【答案】(1)证明:四边形是矩形,
,,,
,
,
,
,
,
∽,
(2)
【解析】【解答】解:(2)∵矩形ABCD,,
∴DC=AB=6,
在Rt△CDE中,由勾股定理可得:,
∵∽,
∴,
∴,
∴,
故答案为:.
【分析】(1)利用角的运算和等量代换可得,再结合,即可得到∽;
(2)先利用勾股定理求出DE的长,再利用相似三角形的性质可得,再将数据代入求出AF的长即可.
19.【答案】解:∵△ADE和△ABC的相似比是1:2,
又∵△ADE的面积是1,
∴S四边形
【解析】【分析】利用相似三角形的面积比等于相似比的平方,利用△ADE的面积,可求出△ABC的面积,再利用四边形DBCE的面积等于△ABC的面积减去△ADE的面积,代入计算可求出结果.
20.【答案】(1)解:∵ 平分 ,
∴ ,
∵ ,
∴ .
(2)解: ;
∵ 是 的中点,
∴ ,
∴ .
∵ 平分 ,
∴ ,
∴ ,
∴ .
【解析】【分析】(1)证明∠DAC=∠CAB,∠ADC=∠ACB=90°,即可解决问题;(2)根据直角三角形的性质,可得CE与AE的关系,根据等腰三角形的性质,可得∠EAC=∠ECA,根据角平分线的定义,可得∠CAD=∠CAB,根据平行线的判定,可得答案.
21.【答案】(1)解:(1)过P作PE⊥OA于E,
∵PQ∥OA,PM∥OB,
∴四边形OMPQ为平行四边形,
∴PM=OQ=1,∠PME=∠AOB=60°,
∴PE=PM sin60°=,ME=,
∴CE=OC﹣OM﹣ME=,
∴tan∠PCE==,
∴∠PCE=30°,
∴∠CPM=90°,
又∵PM∥OB,
∴∠CNO=∠CPM=90°,
则CN⊥OB
(2)解:①﹣的值不发生变化,理由如下:设OM=x,ON=y,∵四边形OMPQ为菱形,∴OQ=QP=OM=x,NQ=y﹣x,∵PQ∥OA,∴∠NQP=∠O,又∵∠QNP=∠ONC,∴△NQP∽△NOC,∴=,即=,
∴6y﹣6x=xy.两边都除以6xy,得﹣=,即﹣=.
②过P作PE⊥OA于E,过N作NF⊥OA于F,则S1=OM PE,S2=OC NF,∴=.∵PM∥OB,∴∠PMC=∠O,又∵∠PCM=∠NCO,∴△CPM∽△CNO,∴==,∴==﹣(x﹣3)2+,∵0<x<6,则根据二次函数的图象可知,0<≤.
【解析】【分析】(1)过P作PE⊥OA于E,利用两组对边平行的四边形为平行四边形得到OMPQ为平行四边形,利用平行四边形的对边相等,对角相等得到PM=OQ=1,∠PME=∠AOB=60°,进而求出PE与ME的长,得到CE的长,求出tan∠PCE的值,利用特殊角的三角函数值求出∠PCE的度数,得到PM于NC垂直,而PM与ON平行,即可得到CN与OB垂直;
(2)﹣的值不发生变化,理由如下:设OM=x,ON=y,根据OMPQ为菱形,得到PM=PQ=OQ=x,QN=y﹣x,根据平行得到三角形NQP与三角形NOC相似,由相似得比例即可确定出所求式子的值;
②过P作PE⊥OA于E,过N作NF⊥OA于F,表示出菱形OMPQ的面积为S1,△NOC的面积为S2,得到,由PM与OB平行,得到三角形CPM与三角形CNO相似,由相似得比例求出所求式子 的范围即可.
22.【答案】(1)解:四边形是平行四边形,
,
,
,
,
,
;
(2)解:∽,
,
的面积为,
的面积是,
四边形是平行四边形,
,
,
,
的面积,
平行四边形的面积.
【解析】【分析】(1)根据平行四边形的性质可得DE∥BF,证明△ADE∽△ABC,然后根据相似三角形的对应边成比例进行计算;
(2)根据相似三角形的面积比等于相似比的平方可得 ,则△ABC的面积是16,由平行四边形的性质可得EF∥AB,证明△EFC∽△ABC,根据相似三角形的面积比等于相似比的平方可得△EFC的面积,据此求解.
23.【答案】(1)证明:连接OD,AD, ∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴BD=CD, ∵OA=OB,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)解:∵OD∥AE, ∴△ODF∽△AEF, ∴ ,
∵AB=4,AE=3,
∴ , ∴BF=2.
【解析】【分析】(1)作辅助线,根据等腰三角形三线合一得BD=CD,根据三角形的中位线可得OD∥AC,所以得OD⊥EF,从而得结论;(2)证明△ODF∽△AEF,列比例式可得结论.
24.【答案】(1)解:将点C(2,2)代入直线l1:y=﹣x+b中,得-2+b=2,
解得b=4,
∴直线l1:y=﹣x+4;
将点C(2,2)代入直线l2:y=kx+1中,得2k+1=2,
解得k= ,
∴直线l2:y= x+1;
(2)解:①∵l⊥x轴,E(m,0).
∴点F( ),G( ),
当m<2时, ,解得m=0;
当m>2时, ,解得m=4;
∴当GF的长为3时,m的值为0或4;
.
②∵ =3,
∴GE=3GF,
当m<2时, ,解得 ;
当m>2时, ,解得 ;
∴ 或 ;
(3)解:过点P作PH⊥AB于H,
∵y=﹣x+4,
∴A(4,0),B(0,4),
∴OA=OB=4,
∴∠BAO=∠ABO= , ,
∴∠HAP=∠HPA= ,
∴AH=PH,
设PH=a,
∵∠OBE=∠ABP,∠BOE=∠BHP= ,
∴△BHP∽△BOE,
∴ ,
∴ ,
解得 ,
∴ ,
∴P( ),
设直线BP的解析式为y=nk+b,
∴ ,解得 ,
∴ .
.
【解析】【分析】(1)将C(2,2)代入y=-x+b中可得b的值,进而可得直线l1的解析式,将C(2,2)代入y=kx+1中求出k的值,进而可得直线l2的解析式;
(2)①易得F(m,-m+4),G(m,
m+1),表示出GF,然后根据GF=3求解即可;
②由已知条件可得GE=3GF,然后分别表示出GE、GF,根据GE=3GF求解即可;
(3)过点P作PH⊥AB于点H,易得A(4,0),B(0,4),则OA=OB=4,利用勾股定理求出AB,设PH=a,证明△BHP∽△BOE,根据相似三角形的性质求出a,进而可得AP,求出点P的坐标,设直线BP的解析式为y=kx+b,然后将点B、P的坐标代入求出k、b,据此可得直线BP的解析式.
1 / 1
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
