京改版九年级数学上册第十九章二次函数与反比例函数 单元复习题(含解析)
文档属性
| 名称 | 京改版九年级数学上册第十九章二次函数与反比例函数 单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 527.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 11:04:23 | ||
图片预览


文档简介
京改版九年级数学上册第十九章二次函数与反比例函数单元复习题
一、单选题
1.已知矩形的长为,宽为,面积为,则与之间的函数关系用图象表示大致是( )
A. B. C. D.
2.函数y=x2+x﹣2的图象与y轴的交点坐标是( )
A.(﹣2,0) B.(1,0) C.(0,﹣2) D.(0,2)
3.下列函数是二次函数的是( )
A.y=3x+1 B.y=ax2+bx+c
C.y=x2+3 D.y=(x﹣1)2﹣x2
4.二次函数y=2x2的图象可以看做抛物线y=2( x-1)2+3怎样平移得到的( )
A.向左平移1个单位,再向下平移3个单位
B.向左平移1个单位,再向上平移3个单位
C.向右平移1个单位,再向上平移3个单位
D.向右平移1个单位,再向下平移3个单位
5.将二次函数y=2x2﹣4x﹣1的图象向右平移3个单位,则平移后的二次函数的顶点是( )
A.(﹣2,﹣3) B.(4,3)
C.(4,﹣3) D.(1,0)
6.如图,菱形OABC的顶点C的坐标为(3,4).顶点A在x轴的正半轴上,反比例函数y= (x>0)的图象经过顶点B,则k的值为( )
A.12 B.20 C.24 D.32
7.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③3a+c<0;④当y>0时,x的取值范围是﹣1≤x<3;⑤当x<0时,y随x增大而增大,其中结论正确的个数是( )
A.5个 B.4个 C.3个 D.2个
8.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),与y轴的交点B在点(0,2)与点(0,3)之间(不包括这两点),对称轴为直线x=2.有以下结论:①abc<0;②5a+3b+c>0;③-<a<-;④若点M(-9a,y1),N(a,y2)在抛物线上,则y1<y2.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
9.点A在反比例函数y= 图象上,且位于第二象限,过点A作AB⊥y轴于点B,已知△ABO面积为3,则k的值是 .
10.如图,直线y =mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是 .
11.如图,已知双曲线 , ,点P为双曲线 上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 于D、C两点,则△PCD的面积为 .
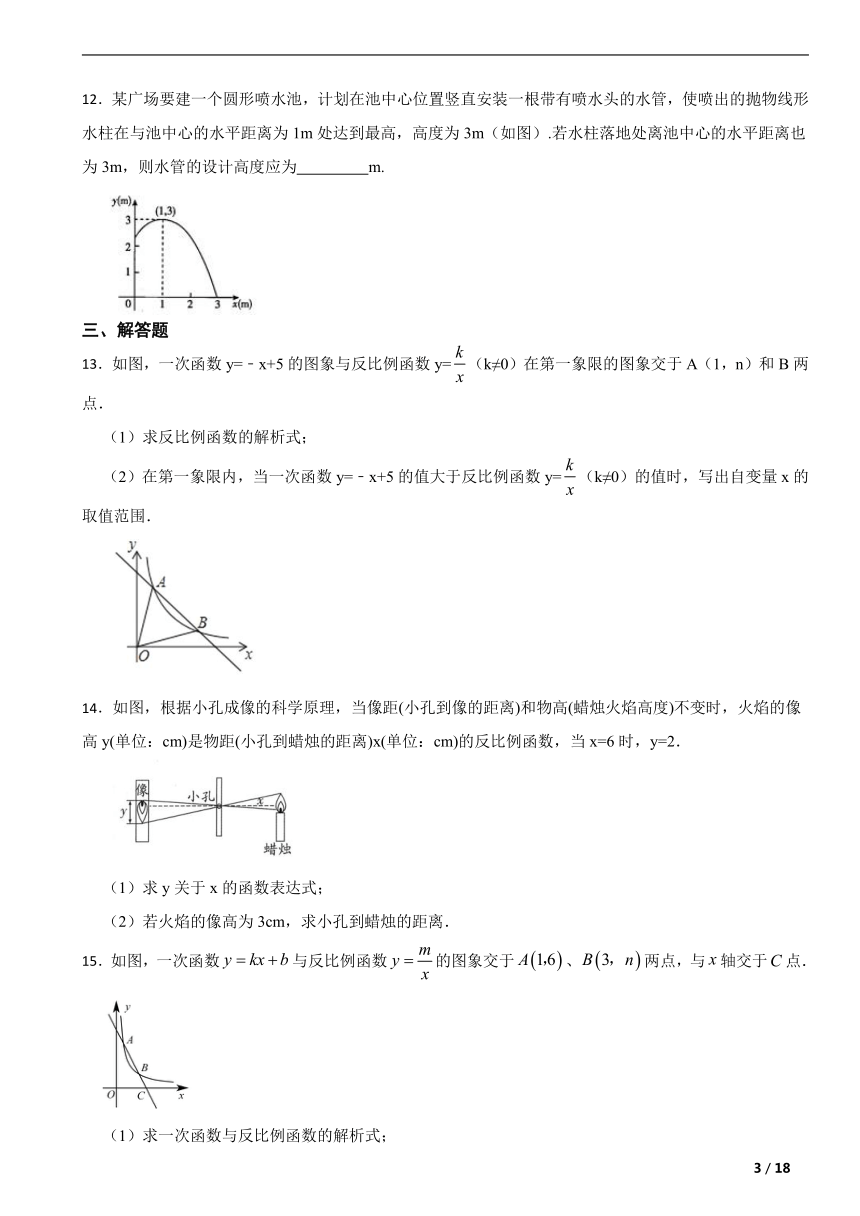
12.某广场要建一个圆形喷水池,计划在池中心位置竖直安装一根带有喷水头的水管,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m(如图).若水柱落地处离池中心的水平距离也为3m,则水管的设计高度应为 m.
三、解答题
13.如图,一次函数y=﹣x+5的图象与反比例函数y=(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式;
(2)在第一象限内,当一次函数y=﹣x+5的值大于反比例函数y=(k≠0)的值时,写出自变量x的取值范围.
14.如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2.
(1)求y关于x的函数表达式;
(2)若火焰的像高为3cm,求小孔到蜡烛的距离.
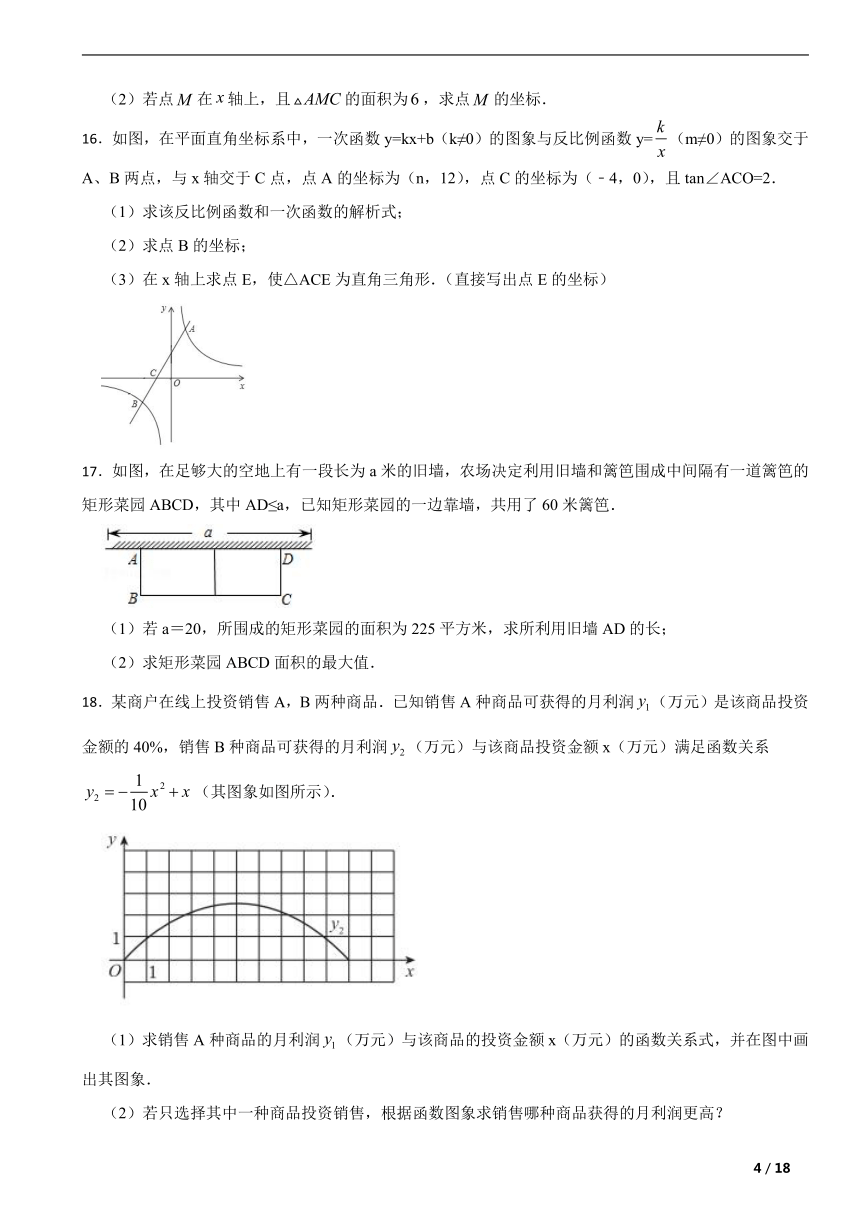
15.如图,一次函数与反比例函数的图象交于、两点,与轴交于点.
(1)求一次函数与反比例函数的解析式;
(2)若点在轴上,且的面积为,求点的坐标.
16.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(﹣4,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
17.如图,在足够大的空地上有一段长为a米的旧墙,农场决定利用旧墙和篱笆围成中间隔有一道篱笆的矩形菜园ABCD,其中AD≤a,已知矩形菜园的一边靠墙,共用了60米篱笆.
(1)若a=20,所围成的矩形菜园的面积为225平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
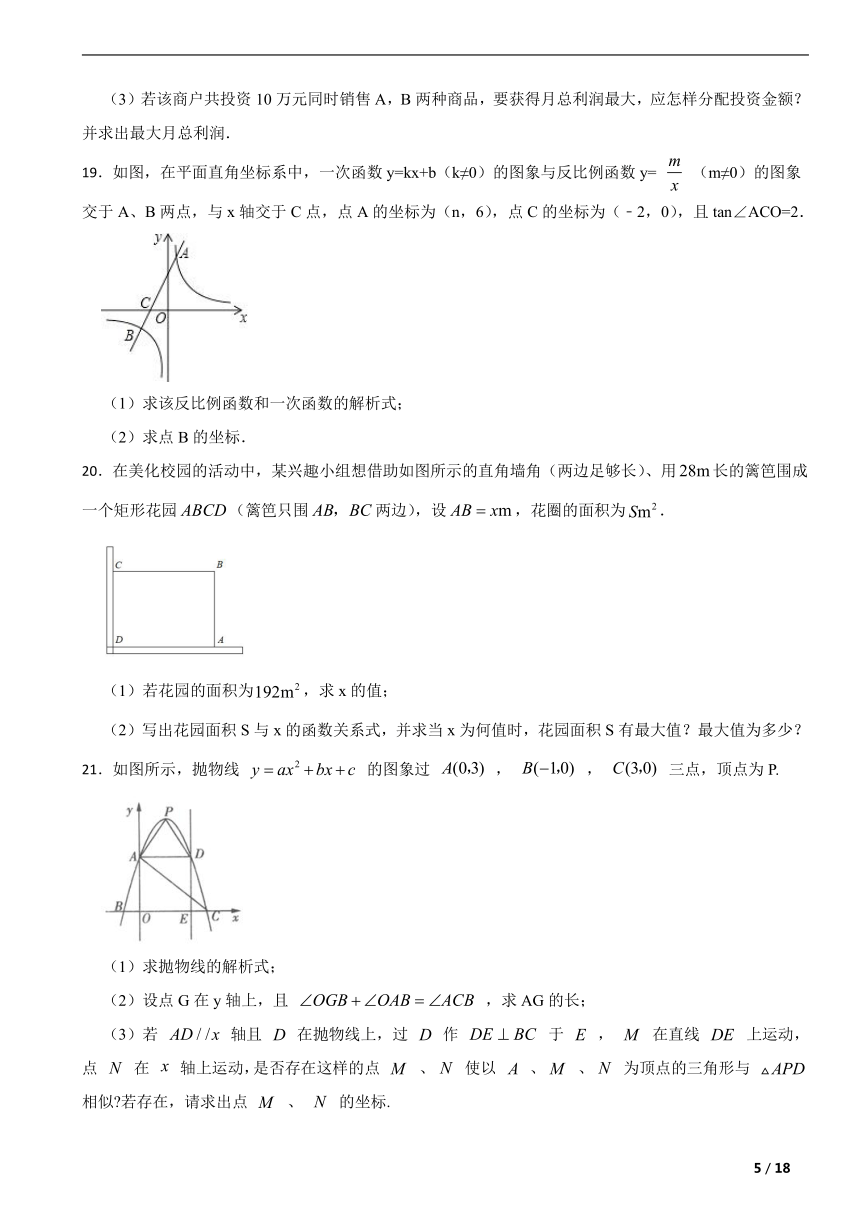
18.某商户在线上投资销售A,B两种商品.已知销售A种商品可获得的月利润(万元)是该商品投资金额的40%,销售B种商品可获得的月利润(万元)与该商品投资金额x(万元)满足函数关系(其图象如图所示).
(1)求销售A种商品的月利润(万元)与该商品的投资金额x(万元)的函数关系式,并在图中画出其图象.
(2)若只选择其中一种商品投资销售,根据函数图象求销售哪种商品获得的月利润更高?
(3)若该商户共投资10万元同时销售A,B两种商品,要获得月总利润最大,应怎样分配投资金额?并求出最大月总利润.
19.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.
20.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长)、用长的篱笆围成一个矩形花园(篱笆只围两边),设,花圈的面积为.
(1)若花园的面积为,求x的值;
(2)写出花园面积S与x的函数关系式,并求当x为何值时,花园面积S有最大值?最大值为多少?
21.如图所示,抛物线 的图象过 , , 三点,顶点为P.
(1)求抛物线的解析式;
(2)设点G在y轴上,且 ,求AG的长;
(3)若 轴且 在抛物线上,过 作 于 , 在直线 上运动,点 在 轴上运动,是否存在这样的点 、 使以 、 、 为顶点的三角形与 相似 若存在,请求出点 、 的坐标.
答案解析部分
1.【答案】A
【解析】【解答】解:由题意知:(x>0,y>0),因为k=9>0,反比例函数图象在第一、三象限,根据实际情况可知,该函数图象只能在第一象限,故A选项正确.
故答案为:A.
【分析】反比函数(k≠0)当k>0时,函数图象在第一、三象限;当k<0时,函数图象在第二、四象限,此题目是实际应用的题目,x、y均大于零,故其图象在第一象限.
2.【答案】C
【解析】【解答】解:令x=0,
y=x2+x﹣2=-2
即函数y=x2+x﹣2的图象与y轴的交点坐标是(0,-2)
故答案为:C.
【分析】将x=0代入y=x2+x﹣2求解即可。
3.【答案】C
【解析】【解答】解:A. 是一次函数,故该选项不符合题意;
B.当 时, 不是二次函数,故该选项不符合题意;
C. 是二次函数,故该选项符合题意;
D. 可整理为 ,是一次函数,故该选项不符合题意.
故答案选C.
【分析】根据二次函数的定义对每个选项进行判断即可。
4.【答案】A
【解析】【解答】可以由二次函数y=2( x-1)2+3先向左平移1个单位,再向下平移3个单位得到.
故答案为:A.
【分析】按照“左加右减,上加下减”的规律,可以由二次函数y=2( x-1)2+3先向左平移1个单位,再向下平移3个单位得到 。
5.【答案】C
【解析】【解答】解:∵y=2x2﹣4x﹣1=2(x2﹣2x)﹣1=2(x﹣1)2﹣3;
∴图象向右平移3个单位长度后,得出:y=2(x﹣1﹣3)2﹣3,即y=2(x﹣4)2﹣3
得到顶点坐标为(4,﹣3).
故选C.
【分析】用配方法可将抛物线一般式转化为顶点式,再利用平移规律求平移后的顶点坐标.
6.【答案】D
【解析】【解答】解:过C点作CD⊥x轴,垂足为D,
∵点C的坐标为(3,4),
∴OD=3,CD=4,
∴OC= = =5,
∴OC=BC=5,
∴点B坐标为(8,4),
∵反比例函数y= (x>0)的图象经过顶点B,
∴k=32,
故选:D.
【分析】过C点作CD⊥x轴,垂足为D,根据点C坐标求出OD、CD、BC的值,进而求出B点的坐标,即可求出k的值.
7.【答案】C
【解析】【解答】∵抛物线与x轴有两个交点,
∴ >0,
∴结论①符合题意;
∵对称轴x= =1,
∴b= -2a,
∵抛物线x轴的一个交点坐标为(﹣1,0),
∴a-b+c=0,
∴3a+c=0,
∴结论②符合题意,
∴结论③不符合题意;
根据图像,可知,当满足-1<x<3时,y>0,
∴结论④不符合题意;
∵当x<1时,y随x增大而增大,
∴当x<0时,y随x增大而增大,
∴结论⑤是正确的;
故答案为:C.
【分析】根据抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0), 再结合函数图象一一判断即可。
8.【答案】C
【解析】【解答】解:①由开口可知:a﹤0,
∵对称轴
∴b﹥0,
由抛物线与y轴的交点可知:c﹥0,
∴abc﹤0,故①符合题意;
②对称轴x=,
∴ b=-4a,
∴5a+3b+c=5a- 12a+c=-7a+c,
∵a﹤0,c﹥0,
∴-7a+c﹥0,
∴5a+3b+c﹥ 0,故②符合题意;
③∵x=-1,y=0,
∴a-b+c=0,
∴ b=-4a,
∴c=-5a,
∵2﹤c﹤3,
∴2﹤-5a﹤3,
∴﹤a﹤,故③符合题意;
④点M(-9a,y1),N(,y2) 在抛物线上,
则
当时,y1﹥y2
当-时,y1﹤y2
故④不符合题意.
故答案为: C.
【分析】利用二次函数的图象与性质,对每个结论一一判断即可。
9.【答案】-6
【解析】【解答】解:∵AB⊥y轴,
∴S△OAB= |k|,
∴ |k|=3,
∵k<0,
∴k=﹣6.
故答案为:﹣6.
【分析】根据反比例函数k的几何意义可得S△OAB=可求解.
10.【答案】x<-1或x>4
【解析】【解答】观察函数图象可知:当x<-1或x>4时,直线y=mx+n在抛物线y=ax2+bx+c的上方,
∴不等式mx+n>ax2+bx+c的解集为x<-1或x>4.
故答案为x<-1或x>4.
【分析】求关于x的不等式mx+n>ax2+bx+c的解集 ,就是求直线 y =mx+n的图像在抛物线y=ax2+bx+c 的图像的上方的时候相应的自变量的取值,根据图像即可直接得出答案。
11.【答案】
【解析】【解答】解:作CE⊥AO于E,DF⊥CE于F,
∵双曲线 , ,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 于D、C两点,
∴矩形BCEO的面积为:xy=1,
∵BC×BO=1,BP×BO=4,
∴BC= BP,
∵AO×AD=1,AO×AP=4,
∴AD= AP,
∵PA PB=4,
∴ PB× PA= PA PB=CP×DP= ×4= ,
∴△PCD的面积为: .
故答案为: .
【分析】根据BC×BO=1,BP×BO=4,得出BC= BP,再利用AO×AD=1,AO×AP=4,得出AD= AP,进而求出 PB× PA=CP×DP= ,即可得出答案.
12.【答案】
【解析】【解答】 解:由题意设喷出的抛物线形水柱高度y(单位:m)与水平距离x(单位:m)满足关系式y=a(x-1)2+3,
当x=3时,y=a(3-1)2+3 =0,求得a= ,
令x=0,可得y=(0-1)2+3 =,
水管的设计高度应为.
故答案为:.
【分析】根据题意设喷出的抛物线形水柱关系式为y=a(x-1)2+3,代入(3,0)求出a的值,进而令x=0,求水管的设计高度.
13.【答案】解:(1)∵一次函数y=﹣x+5的图象过点A(1,n),
∴n=﹣1+5,
∴n=4,
∴点A坐标为(1,4),
∵反比例函数y=(k≠0)过点A(1,4),
∴k=4,
∴反比例函数的解析式为y=;
(2)联立 ,
解得 或,
即点B的坐标(4,1),
若一次函数y=﹣x+5的值大于反比例函数y=(k≠0)的值,
则1<x<4.
【解析】【分析】(1)首先求出点A的坐标,进而即可求出反比例函数系数k的值;
(2)联立反比例函数和一次函数解析式,求出交点B的坐标,结合图形即可求出x的取值范围.
14.【答案】(1)由题意设y= ,把x=6,y=2代人,得k= 6×2= 12,
∴ y关于x的函数表达式为y=
(2)把y=3代人y=,得x=4,∴小孔到蜡烛的距离为4 cm.
15.【答案】(1)解:把代入得:,
∴反比例函数的解析式为,
把代入得:,
∴的坐标为,
∴,解得,
∴一次函数的解析式为
(2)解:把代入中,得,
∴点的坐标为
∵点的纵坐标等于6,
∴,
∴,
∴点的坐标为或.
【解析】【分析】(1)本题考查函数的交点和求函数解析式。点在函数上,则点的横纵坐标满足函数解析式,利用A(1,6)可得出反比例的解析式,根据B(3,n)在反比例函数,可求出n值,根据A、B两点坐标,待定系数法求出一次函数解析式。(2)求出C的坐标,根据的面积为和点A的纵坐标,可计算出CM=2,则M在C左侧右侧两个坐标。
16.【答案】解:(1)过点A作AD⊥x轴于D,∵C的坐标为(﹣4,0),A的坐标为(n,12),∴AD=12,CD=n+4,∵tan∠ACO=2,∴==2,解得:n=2,∴A(2,12),把A(2,12)代入y=,得m=2×12=24,∴反比例函数表达式为:y=,又∵点A(2,12),C(﹣4,0)在直线y=kx+b上,∴2k+b=12,﹣4k+b=0,解得:k=2,b=8,∴一次函数的表达式为:y=2x+8;(2)由方程组 ,解得: , ,∵A(2,12),∴B(﹣6,﹣4);(3)分两种情况:①当AE⊥x轴时,即点E与点D重合,此时E1(2,0);②当EA⊥AC时,此时△ADE∽△CDA,则=,DE==24,又∵D的坐标为(2,0),∴E2(26,0).综上所述,所求点E的坐标为E1(2,0),E2(26,0).
【解析】【分析】(1)过点A作AD⊥x轴于D,根据A、C的坐标求出AD=12,CD=n+4,已知tan∠ACO=2,可求出n的值,把点的坐标代入解析式即可求得反比例函数和一次函数解析式;
(2)将反比例函数和一次函数的解析式联立,解方程组即可求得点B的坐标;
(3)分两种情况:①AE⊥x轴,②EA⊥AC,分别写出E的坐标即可.
17.【答案】(1)解:设AD=xm,则AB=m,
根据题意得x =225,
解得x1=15,x2=45,
∵AD≤a=20,
∴AD=15,
答:AD的长为15m;
(2)解:设AD=xm.
∴S=x =﹣(x2﹣60x)=﹣(x﹣30)2+300,
当a≥30时,则x=30时取S最大值,最大值为300平方米,
当0<a<30时,则当0<x≤a时,S随x的增大而增大,当x=a时,S的最大值为﹣a2+20a,
综上所述,当a≥30时,矩形菜园ABCD面积的最大值为300m2;当0<a<30时,矩形菜园ABCD面积的最大值为﹣a2+20a.
【解析】【分析】(1)设AD=xm,观察图形,利用矩形菜园的一边靠墙,共用了60米篱笆,可表示出AB的长,再利用矩形的面积等于长×宽,可得到关于x的方程,解方程求出x的值,再根据AD≤a可得到AD的长;
(2)设AD=xm,矩形的面积为S,利用矩形的面积公式可得到S与x之间的函数解析式,利用二次函数的性质,分情况讨论:当a≥30时;当0<a<30时,可得到矩形的最大面积.
18.【答案】(1)解:由题意知,
∴函数关系式为;
图象如下:
(2)解:令,则
解得,
∴当时,两种产品的月利润相同;
由图象可知,当时,,此时销售B种商品月利润更高;
当时,,此时销售A种商品月利润更高;
∴当时,选择B种商品;当时,均可;当时,选择A种商品.
(3)解:设投资销售B商品为a万元,A商品为万元,月总利润为w
由题意知,
∵
∴时,w最大,值为4.9万元
∴应投资销售B商品为3万元,则A商品为7万元,月总利润为4.9万元.
【解析】【分析】(1)由已知直接得出;再画出图象即可;
(2)由图象直接得出答案;
(3)设投资销售B商品为a万元,A商品为万元,月总利润为w,由题意知,,根据二次函数性质即可得出答案。
19.【答案】(1)解:过点A作AD⊥x轴,垂足为D
由A(n,6),C(﹣2,0)可得,
OD=n,AD=6,CO=2
∵tan∠ACO=2
∴ =2,即 =2
∴n=1
∴A(1,6)
将A(1,6)代入反比例函数,得m=1×6=6
∴反比例函数的解析式为
将A(1,6),C(﹣2,0)代入一次函数y=kx+b,可得
解得
∴一次函数的解析式为y=2x+4
(2)解:由 可得
解得x1=1,x2=﹣3
∵当x=﹣3时,y=﹣2
∴点B坐标为(﹣3,﹣2)
【解析】【分析】本题主要考查了反比例函数与一次函数的交点问题,解决问题的关键是掌握待定系数法求函数解析式.求反比例函数与一次函数的交点坐标时,把两个函数关系式联立成方程组求解,若方程组有解,则两者有交点,若方程组无解,则两者无交点.(1)先过点A作AD⊥x轴,根据tan∠ACO=2,求得点A的坐标,进而根据待定系数法计算两个函数解析式;(2)先联立两个函数解析式,再通过解方程求得交点B的坐标即可.
20.【答案】(1)解:由题意得,,
整理得,
解得,
所以,x的值为12或16
(2)解:由题意得,,
化成顶点式为,
所以,当x为时,花园面积S有最大值,最大值为.
【解析】【分析】(1)根据题意列出方程,再求出x的值即可;
(2)根据题意列出函数解析式,再利用二次函数的性质求解即可。
21.【答案】(1)解:由 可另设解析式为 .
把 代入,得 ,
,
;
(2)解: ,
.
过 作 交 延长线于 .
是等腰直角三角形, .
又 ,
.
.
又 ,
,
同理,当点G在y轴正半轴时,可得AG=1,
或5;
(3)解:由题意得:顶点 .
为等腰直角三角形.
∴只要 也是等腰直角三角形,两个三角形就相似.
①如图1所示, ,
可得 .
.
;
②如图2所示, ,
可得 .
,
;
③如图3所示, ,
可得 .
,
;
④如图4所示,若 ,
则 ,但 ,
∴不存在,
综上,存在三组 点:① 或② 或③ .
【解析】【分析】(1)利用待定系数法求函数解析式;
(2)根据AO=CO=3得到∠OGB+∠OAB=45°,过 作 交 延长线于 ,证得△BHG是等腰直角三角形, ,再证明 求出 , ,即可求出AG;
(3)根据点A、P、D的坐标得到△PAD为等腰直角三角形,分∠AMN、∠ANM、∠MAN是直角,夹直角的两边相等,分别求出点M、N的坐标即可.
1 / 1
一、单选题
1.已知矩形的长为,宽为,面积为,则与之间的函数关系用图象表示大致是( )
A. B. C. D.
2.函数y=x2+x﹣2的图象与y轴的交点坐标是( )
A.(﹣2,0) B.(1,0) C.(0,﹣2) D.(0,2)
3.下列函数是二次函数的是( )
A.y=3x+1 B.y=ax2+bx+c
C.y=x2+3 D.y=(x﹣1)2﹣x2
4.二次函数y=2x2的图象可以看做抛物线y=2( x-1)2+3怎样平移得到的( )
A.向左平移1个单位,再向下平移3个单位
B.向左平移1个单位,再向上平移3个单位
C.向右平移1个单位,再向上平移3个单位
D.向右平移1个单位,再向下平移3个单位
5.将二次函数y=2x2﹣4x﹣1的图象向右平移3个单位,则平移后的二次函数的顶点是( )
A.(﹣2,﹣3) B.(4,3)
C.(4,﹣3) D.(1,0)
6.如图,菱形OABC的顶点C的坐标为(3,4).顶点A在x轴的正半轴上,反比例函数y= (x>0)的图象经过顶点B,则k的值为( )
A.12 B.20 C.24 D.32
7.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③3a+c<0;④当y>0时,x的取值范围是﹣1≤x<3;⑤当x<0时,y随x增大而增大,其中结论正确的个数是( )
A.5个 B.4个 C.3个 D.2个
8.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),与y轴的交点B在点(0,2)与点(0,3)之间(不包括这两点),对称轴为直线x=2.有以下结论:①abc<0;②5a+3b+c>0;③-<a<-;④若点M(-9a,y1),N(a,y2)在抛物线上,则y1<y2.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题
9.点A在反比例函数y= 图象上,且位于第二象限,过点A作AB⊥y轴于点B,已知△ABO面积为3,则k的值是 .
10.如图,直线y =mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是 .
11.如图,已知双曲线 , ,点P为双曲线 上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 于D、C两点,则△PCD的面积为 .
12.某广场要建一个圆形喷水池,计划在池中心位置竖直安装一根带有喷水头的水管,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m(如图).若水柱落地处离池中心的水平距离也为3m,则水管的设计高度应为 m.
三、解答题
13.如图,一次函数y=﹣x+5的图象与反比例函数y=(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式;
(2)在第一象限内,当一次函数y=﹣x+5的值大于反比例函数y=(k≠0)的值时,写出自变量x的取值范围.
14.如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2.
(1)求y关于x的函数表达式;
(2)若火焰的像高为3cm,求小孔到蜡烛的距离.
15.如图,一次函数与反比例函数的图象交于、两点,与轴交于点.
(1)求一次函数与反比例函数的解析式;
(2)若点在轴上,且的面积为,求点的坐标.
16.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(﹣4,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
17.如图,在足够大的空地上有一段长为a米的旧墙,农场决定利用旧墙和篱笆围成中间隔有一道篱笆的矩形菜园ABCD,其中AD≤a,已知矩形菜园的一边靠墙,共用了60米篱笆.
(1)若a=20,所围成的矩形菜园的面积为225平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
18.某商户在线上投资销售A,B两种商品.已知销售A种商品可获得的月利润(万元)是该商品投资金额的40%,销售B种商品可获得的月利润(万元)与该商品投资金额x(万元)满足函数关系(其图象如图所示).
(1)求销售A种商品的月利润(万元)与该商品的投资金额x(万元)的函数关系式,并在图中画出其图象.
(2)若只选择其中一种商品投资销售,根据函数图象求销售哪种商品获得的月利润更高?
(3)若该商户共投资10万元同时销售A,B两种商品,要获得月总利润最大,应怎样分配投资金额?并求出最大月总利润.
19.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.
20.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长)、用长的篱笆围成一个矩形花园(篱笆只围两边),设,花圈的面积为.
(1)若花园的面积为,求x的值;
(2)写出花园面积S与x的函数关系式,并求当x为何值时,花园面积S有最大值?最大值为多少?
21.如图所示,抛物线 的图象过 , , 三点,顶点为P.
(1)求抛物线的解析式;
(2)设点G在y轴上,且 ,求AG的长;
(3)若 轴且 在抛物线上,过 作 于 , 在直线 上运动,点 在 轴上运动,是否存在这样的点 、 使以 、 、 为顶点的三角形与 相似 若存在,请求出点 、 的坐标.
答案解析部分
1.【答案】A
【解析】【解答】解:由题意知:(x>0,y>0),因为k=9>0,反比例函数图象在第一、三象限,根据实际情况可知,该函数图象只能在第一象限,故A选项正确.
故答案为:A.
【分析】反比函数(k≠0)当k>0时,函数图象在第一、三象限;当k<0时,函数图象在第二、四象限,此题目是实际应用的题目,x、y均大于零,故其图象在第一象限.
2.【答案】C
【解析】【解答】解:令x=0,
y=x2+x﹣2=-2
即函数y=x2+x﹣2的图象与y轴的交点坐标是(0,-2)
故答案为:C.
【分析】将x=0代入y=x2+x﹣2求解即可。
3.【答案】C
【解析】【解答】解:A. 是一次函数,故该选项不符合题意;
B.当 时, 不是二次函数,故该选项不符合题意;
C. 是二次函数,故该选项符合题意;
D. 可整理为 ,是一次函数,故该选项不符合题意.
故答案选C.
【分析】根据二次函数的定义对每个选项进行判断即可。
4.【答案】A
【解析】【解答】可以由二次函数y=2( x-1)2+3先向左平移1个单位,再向下平移3个单位得到.
故答案为:A.
【分析】按照“左加右减,上加下减”的规律,可以由二次函数y=2( x-1)2+3先向左平移1个单位,再向下平移3个单位得到 。
5.【答案】C
【解析】【解答】解:∵y=2x2﹣4x﹣1=2(x2﹣2x)﹣1=2(x﹣1)2﹣3;
∴图象向右平移3个单位长度后,得出:y=2(x﹣1﹣3)2﹣3,即y=2(x﹣4)2﹣3
得到顶点坐标为(4,﹣3).
故选C.
【分析】用配方法可将抛物线一般式转化为顶点式,再利用平移规律求平移后的顶点坐标.
6.【答案】D
【解析】【解答】解:过C点作CD⊥x轴,垂足为D,
∵点C的坐标为(3,4),
∴OD=3,CD=4,
∴OC= = =5,
∴OC=BC=5,
∴点B坐标为(8,4),
∵反比例函数y= (x>0)的图象经过顶点B,
∴k=32,
故选:D.
【分析】过C点作CD⊥x轴,垂足为D,根据点C坐标求出OD、CD、BC的值,进而求出B点的坐标,即可求出k的值.
7.【答案】C
【解析】【解答】∵抛物线与x轴有两个交点,
∴ >0,
∴结论①符合题意;
∵对称轴x= =1,
∴b= -2a,
∵抛物线x轴的一个交点坐标为(﹣1,0),
∴a-b+c=0,
∴3a+c=0,
∴结论②符合题意,
∴结论③不符合题意;
根据图像,可知,当满足-1<x<3时,y>0,
∴结论④不符合题意;
∵当x<1时,y随x增大而增大,
∴当x<0时,y随x增大而增大,
∴结论⑤是正确的;
故答案为:C.
【分析】根据抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0), 再结合函数图象一一判断即可。
8.【答案】C
【解析】【解答】解:①由开口可知:a﹤0,
∵对称轴
∴b﹥0,
由抛物线与y轴的交点可知:c﹥0,
∴abc﹤0,故①符合题意;
②对称轴x=,
∴ b=-4a,
∴5a+3b+c=5a- 12a+c=-7a+c,
∵a﹤0,c﹥0,
∴-7a+c﹥0,
∴5a+3b+c﹥ 0,故②符合题意;
③∵x=-1,y=0,
∴a-b+c=0,
∴ b=-4a,
∴c=-5a,
∵2﹤c﹤3,
∴2﹤-5a﹤3,
∴﹤a﹤,故③符合题意;
④点M(-9a,y1),N(,y2) 在抛物线上,
则
当时,y1﹥y2
当-时,y1﹤y2
故④不符合题意.
故答案为: C.
【分析】利用二次函数的图象与性质,对每个结论一一判断即可。
9.【答案】-6
【解析】【解答】解:∵AB⊥y轴,
∴S△OAB= |k|,
∴ |k|=3,
∵k<0,
∴k=﹣6.
故答案为:﹣6.
【分析】根据反比例函数k的几何意义可得S△OAB=可求解.
10.【答案】x<-1或x>4
【解析】【解答】观察函数图象可知:当x<-1或x>4时,直线y=mx+n在抛物线y=ax2+bx+c的上方,
∴不等式mx+n>ax2+bx+c的解集为x<-1或x>4.
故答案为x<-1或x>4.
【分析】求关于x的不等式mx+n>ax2+bx+c的解集 ,就是求直线 y =mx+n的图像在抛物线y=ax2+bx+c 的图像的上方的时候相应的自变量的取值,根据图像即可直接得出答案。
11.【答案】
【解析】【解答】解:作CE⊥AO于E,DF⊥CE于F,
∵双曲线 , ,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 于D、C两点,
∴矩形BCEO的面积为:xy=1,
∵BC×BO=1,BP×BO=4,
∴BC= BP,
∵AO×AD=1,AO×AP=4,
∴AD= AP,
∵PA PB=4,
∴ PB× PA= PA PB=CP×DP= ×4= ,
∴△PCD的面积为: .
故答案为: .
【分析】根据BC×BO=1,BP×BO=4,得出BC= BP,再利用AO×AD=1,AO×AP=4,得出AD= AP,进而求出 PB× PA=CP×DP= ,即可得出答案.
12.【答案】
【解析】【解答】 解:由题意设喷出的抛物线形水柱高度y(单位:m)与水平距离x(单位:m)满足关系式y=a(x-1)2+3,
当x=3时,y=a(3-1)2+3 =0,求得a= ,
令x=0,可得y=(0-1)2+3 =,
水管的设计高度应为.
故答案为:.
【分析】根据题意设喷出的抛物线形水柱关系式为y=a(x-1)2+3,代入(3,0)求出a的值,进而令x=0,求水管的设计高度.
13.【答案】解:(1)∵一次函数y=﹣x+5的图象过点A(1,n),
∴n=﹣1+5,
∴n=4,
∴点A坐标为(1,4),
∵反比例函数y=(k≠0)过点A(1,4),
∴k=4,
∴反比例函数的解析式为y=;
(2)联立 ,
解得 或,
即点B的坐标(4,1),
若一次函数y=﹣x+5的值大于反比例函数y=(k≠0)的值,
则1<x<4.
【解析】【分析】(1)首先求出点A的坐标,进而即可求出反比例函数系数k的值;
(2)联立反比例函数和一次函数解析式,求出交点B的坐标,结合图形即可求出x的取值范围.
14.【答案】(1)由题意设y= ,把x=6,y=2代人,得k= 6×2= 12,
∴ y关于x的函数表达式为y=
(2)把y=3代人y=,得x=4,∴小孔到蜡烛的距离为4 cm.
15.【答案】(1)解:把代入得:,
∴反比例函数的解析式为,
把代入得:,
∴的坐标为,
∴,解得,
∴一次函数的解析式为
(2)解:把代入中,得,
∴点的坐标为
∵点的纵坐标等于6,
∴,
∴,
∴点的坐标为或.
【解析】【分析】(1)本题考查函数的交点和求函数解析式。点在函数上,则点的横纵坐标满足函数解析式,利用A(1,6)可得出反比例的解析式,根据B(3,n)在反比例函数,可求出n值,根据A、B两点坐标,待定系数法求出一次函数解析式。(2)求出C的坐标,根据的面积为和点A的纵坐标,可计算出CM=2,则M在C左侧右侧两个坐标。
16.【答案】解:(1)过点A作AD⊥x轴于D,∵C的坐标为(﹣4,0),A的坐标为(n,12),∴AD=12,CD=n+4,∵tan∠ACO=2,∴==2,解得:n=2,∴A(2,12),把A(2,12)代入y=,得m=2×12=24,∴反比例函数表达式为:y=,又∵点A(2,12),C(﹣4,0)在直线y=kx+b上,∴2k+b=12,﹣4k+b=0,解得:k=2,b=8,∴一次函数的表达式为:y=2x+8;(2)由方程组 ,解得: , ,∵A(2,12),∴B(﹣6,﹣4);(3)分两种情况:①当AE⊥x轴时,即点E与点D重合,此时E1(2,0);②当EA⊥AC时,此时△ADE∽△CDA,则=,DE==24,又∵D的坐标为(2,0),∴E2(26,0).综上所述,所求点E的坐标为E1(2,0),E2(26,0).
【解析】【分析】(1)过点A作AD⊥x轴于D,根据A、C的坐标求出AD=12,CD=n+4,已知tan∠ACO=2,可求出n的值,把点的坐标代入解析式即可求得反比例函数和一次函数解析式;
(2)将反比例函数和一次函数的解析式联立,解方程组即可求得点B的坐标;
(3)分两种情况:①AE⊥x轴,②EA⊥AC,分别写出E的坐标即可.
17.【答案】(1)解:设AD=xm,则AB=m,
根据题意得x =225,
解得x1=15,x2=45,
∵AD≤a=20,
∴AD=15,
答:AD的长为15m;
(2)解:设AD=xm.
∴S=x =﹣(x2﹣60x)=﹣(x﹣30)2+300,
当a≥30时,则x=30时取S最大值,最大值为300平方米,
当0<a<30时,则当0<x≤a时,S随x的增大而增大,当x=a时,S的最大值为﹣a2+20a,
综上所述,当a≥30时,矩形菜园ABCD面积的最大值为300m2;当0<a<30时,矩形菜园ABCD面积的最大值为﹣a2+20a.
【解析】【分析】(1)设AD=xm,观察图形,利用矩形菜园的一边靠墙,共用了60米篱笆,可表示出AB的长,再利用矩形的面积等于长×宽,可得到关于x的方程,解方程求出x的值,再根据AD≤a可得到AD的长;
(2)设AD=xm,矩形的面积为S,利用矩形的面积公式可得到S与x之间的函数解析式,利用二次函数的性质,分情况讨论:当a≥30时;当0<a<30时,可得到矩形的最大面积.
18.【答案】(1)解:由题意知,
∴函数关系式为;
图象如下:
(2)解:令,则
解得,
∴当时,两种产品的月利润相同;
由图象可知,当时,,此时销售B种商品月利润更高;
当时,,此时销售A种商品月利润更高;
∴当时,选择B种商品;当时,均可;当时,选择A种商品.
(3)解:设投资销售B商品为a万元,A商品为万元,月总利润为w
由题意知,
∵
∴时,w最大,值为4.9万元
∴应投资销售B商品为3万元,则A商品为7万元,月总利润为4.9万元.
【解析】【分析】(1)由已知直接得出;再画出图象即可;
(2)由图象直接得出答案;
(3)设投资销售B商品为a万元,A商品为万元,月总利润为w,由题意知,,根据二次函数性质即可得出答案。
19.【答案】(1)解:过点A作AD⊥x轴,垂足为D
由A(n,6),C(﹣2,0)可得,
OD=n,AD=6,CO=2
∵tan∠ACO=2
∴ =2,即 =2
∴n=1
∴A(1,6)
将A(1,6)代入反比例函数,得m=1×6=6
∴反比例函数的解析式为
将A(1,6),C(﹣2,0)代入一次函数y=kx+b,可得
解得
∴一次函数的解析式为y=2x+4
(2)解:由 可得
解得x1=1,x2=﹣3
∵当x=﹣3时,y=﹣2
∴点B坐标为(﹣3,﹣2)
【解析】【分析】本题主要考查了反比例函数与一次函数的交点问题,解决问题的关键是掌握待定系数法求函数解析式.求反比例函数与一次函数的交点坐标时,把两个函数关系式联立成方程组求解,若方程组有解,则两者有交点,若方程组无解,则两者无交点.(1)先过点A作AD⊥x轴,根据tan∠ACO=2,求得点A的坐标,进而根据待定系数法计算两个函数解析式;(2)先联立两个函数解析式,再通过解方程求得交点B的坐标即可.
20.【答案】(1)解:由题意得,,
整理得,
解得,
所以,x的值为12或16
(2)解:由题意得,,
化成顶点式为,
所以,当x为时,花园面积S有最大值,最大值为.
【解析】【分析】(1)根据题意列出方程,再求出x的值即可;
(2)根据题意列出函数解析式,再利用二次函数的性质求解即可。
21.【答案】(1)解:由 可另设解析式为 .
把 代入,得 ,
,
;
(2)解: ,
.
过 作 交 延长线于 .
是等腰直角三角形, .
又 ,
.
.
又 ,
,
同理,当点G在y轴正半轴时,可得AG=1,
或5;
(3)解:由题意得:顶点 .
为等腰直角三角形.
∴只要 也是等腰直角三角形,两个三角形就相似.
①如图1所示, ,
可得 .
.
;
②如图2所示, ,
可得 .
,
;
③如图3所示, ,
可得 .
,
;
④如图4所示,若 ,
则 ,但 ,
∴不存在,
综上,存在三组 点:① 或② 或③ .
【解析】【分析】(1)利用待定系数法求函数解析式;
(2)根据AO=CO=3得到∠OGB+∠OAB=45°,过 作 交 延长线于 ,证得△BHG是等腰直角三角形, ,再证明 求出 , ,即可求出AG;
(3)根据点A、P、D的坐标得到△PAD为等腰直角三角形,分∠AMN、∠ANM、∠MAN是直角,夹直角的两边相等,分别求出点M、N的坐标即可.
1 / 1
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
