江苏省沭阳高级中学2008-2009学年度第二学期高二单元测试-空间向量
文档属性
| 名称 | 江苏省沭阳高级中学2008-2009学年度第二学期高二单元测试-空间向量 |
|
|
| 格式 | zip | ||
| 文件大小 | 187.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-25 00:00:00 | ||
图片预览

文档简介
江苏省沭阳高级中学2008-2009学年度第二学期高二单元测试
空间向量
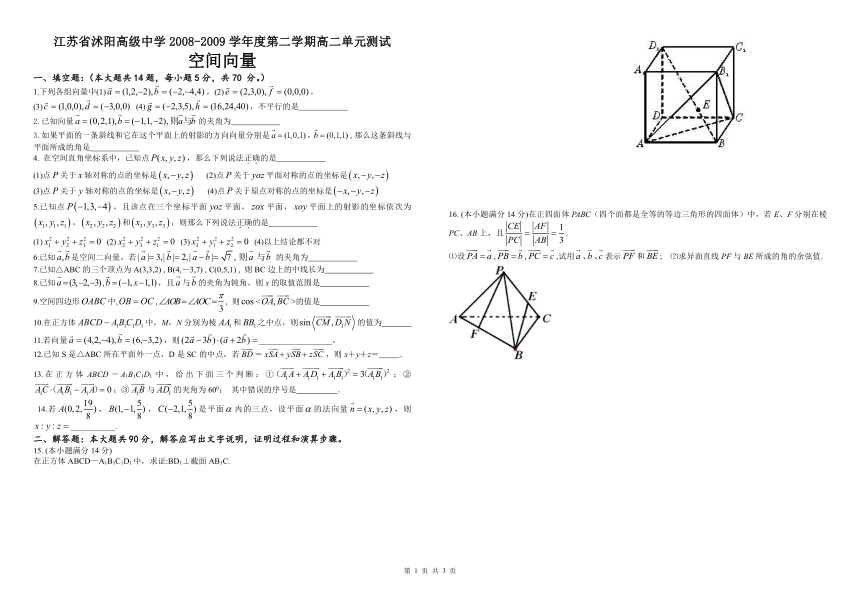
一、填空题:(本大题共14题,每小题5分,共70 分。)
1.下列各组向量中(1),(2),
(3) (4),不平行的是
2.已知向量的夹角为
3.如果平面的一条斜线和它在这个平面上的射影的方向向量分别是,,那么这条斜线与平面所成的角是
4. 在空间直角坐标系中,已知点,那么下列说法正确的是
(1)点关于轴对称的点的坐标是 (2)点关于平面对称的点的坐标是
(3)点关于轴对称的点的坐标是 (4)点关于原点对称的点的坐标是
5.已知点,且该点在三个坐标平面平面,平面,平面上的射影的坐标依次为,和,则那么下列说法正确的是
(1) (2) (3) (4)以上结论都不对
6.已知是空间二向量,若的夹角为
7.已知△ABC的三个顶点为A(3,3,2) , B(4,-3,7) , C(0,5,1) , 则BC边上的中线长为
8.已知,,且与的夹角为钝角,则x的取值范围是
9.空间四边形中,,, 则<>的值是
10.在正方体中,M,N分别为棱和之中点,则的值为
11.若向量,则__________________。
12.已知S是△ABC所在平面外一点,D是SC的中点,若=,则x+y+z= .
13.在正方体ABCD-A1B1C1D1中,给出下面三个判断:①;②;③与的夹角为600; 其中错误的序号是 .
14.若,,是平面内的三点,设平面的法向量,则___________.
二、解答题:本大题共90分,解答应写出文字说明,证明过程和演算步骤。
15. (本小题满分14分)
在正方体ABCD—A1B1C1D1中,求证:BD1⊥截面AB1C.
16. (本小题满分14分)在正四面体PABC(四个面都是全等的等边三角形的四面体)中,若E、F分别在棱PC、AB上,且.
⑴设,,,试用表示和; ⑵求异面直线PF与BE所成的角的余弦值.
17. (本小题满分14分)
如图,直三棱柱ABC—A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点,(1)求(2)求(3)(14分)
18(本小题满分16分)
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(Ⅰ)证明AB⊥平面VAD.
(Ⅱ)求面VAD与面VDB所成的二面角的大小.
19. (本小题满分16分)已知是空间的一个单位正交基底,设
⑴证明:也是空间的一个基底;
⑵若向量在基底下的坐标为,求向量在基底下的坐标.
20.(本小题满分16分)
如图,在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AD上移动.
(1)证明:D1E⊥A1D;
(2)AE等于何值时,二面角D1—EC—D的大小为.
江苏省沭阳高级中学2008-2009学年度第二学期高二单元测试
空间向量参考答案
一、填空题:(本大题共14题,每小题5分,共70 分。)
1、(4) 2、90°3、60° 4、4 5、1 6、60°7、3 8、(-2,)∪(,+∞) 9、 10、
11. 12. 13.③ 14.
二、解答题:本大题共90分,解答应写出文字说明,证明过程和演算步骤。
15. (本小题满分14分)
.法一:综合法证明:连结, ∵,,∴.
又∵,,∴
∴,同理BD1⊥AB1,∵∴BD1⊥面ACB1.
法二: 坐标法证明:先证明BD1⊥AC
∵=++,=+∴ =(+ +) (+)= + = - =||2-||2=0
∴BD1⊥AC,同理可证BD1⊥AB1,∵ 于是BD1⊥平面ACB1
16. . (本小题满分14分)
⑴====,
==
⑵不妨设棱长为1,则,
∴=,,易知
∴异面直线PF与BE所成的角的余弦值为
17. (本小题满分14分)
解:(1)以射线建立坐标系,则B(0,1,0)
18.. (本小题满分16分)
证明:(Ⅰ)作AD的中点O,则VO⊥底面ABCD.建立如图空间直角坐标系,并设正方形边长为1,
则A(,0,0),B(,1,0),C(-,1,0),D(-,0,0),V(0,0,),
∴
由 又AB∩AV=A∴AB⊥平面VAD
(Ⅱ)由(Ⅰ)得是面VAD的法向量,设是面VDB的法向量,则
∴,
又由题意知,面VAD与面VDB所成的二面角,所以其大小为
19. . (本小题满分16分)⑴假设共面,则存在实数使∴,
∴∵∴这不可能.
∴不共面∴也是空间的一个基底.
⑵
20. . (本小题满分16分)解:以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0)C(0,2,0)
(1)
(2)因为E为AB的中点,则E(1,1,0),从而,
,设平面ACD1的法向量为,则
也即,得,从而,所以点E到平面AD1C的距离为
(3)设平面D1EC的法向量,∴
由 令b=1, ∴c=2,a=2-x,
∴
依题意
∴(不合,舍去), .∴AE=时,二面角D1—EC—D的大小为.
PAGE
第 1 页 共 3 页
空间向量
一、填空题:(本大题共14题,每小题5分,共70 分。)
1.下列各组向量中(1),(2),
(3) (4),不平行的是
2.已知向量的夹角为
3.如果平面的一条斜线和它在这个平面上的射影的方向向量分别是,,那么这条斜线与平面所成的角是
4. 在空间直角坐标系中,已知点,那么下列说法正确的是
(1)点关于轴对称的点的坐标是 (2)点关于平面对称的点的坐标是
(3)点关于轴对称的点的坐标是 (4)点关于原点对称的点的坐标是
5.已知点,且该点在三个坐标平面平面,平面,平面上的射影的坐标依次为,和,则那么下列说法正确的是
(1) (2) (3) (4)以上结论都不对
6.已知是空间二向量,若的夹角为
7.已知△ABC的三个顶点为A(3,3,2) , B(4,-3,7) , C(0,5,1) , 则BC边上的中线长为
8.已知,,且与的夹角为钝角,则x的取值范围是
9.空间四边形中,,, 则<>的值是
10.在正方体中,M,N分别为棱和之中点,则的值为
11.若向量,则__________________。
12.已知S是△ABC所在平面外一点,D是SC的中点,若=,则x+y+z= .
13.在正方体ABCD-A1B1C1D1中,给出下面三个判断:①;②;③与的夹角为600; 其中错误的序号是 .
14.若,,是平面内的三点,设平面的法向量,则___________.
二、解答题:本大题共90分,解答应写出文字说明,证明过程和演算步骤。
15. (本小题满分14分)
在正方体ABCD—A1B1C1D1中,求证:BD1⊥截面AB1C.
16. (本小题满分14分)在正四面体PABC(四个面都是全等的等边三角形的四面体)中,若E、F分别在棱PC、AB上,且.
⑴设,,,试用表示和; ⑵求异面直线PF与BE所成的角的余弦值.
17. (本小题满分14分)
如图,直三棱柱ABC—A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点,(1)求(2)求(3)(14分)
18(本小题满分16分)
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(Ⅰ)证明AB⊥平面VAD.
(Ⅱ)求面VAD与面VDB所成的二面角的大小.
19. (本小题满分16分)已知是空间的一个单位正交基底,设
⑴证明:也是空间的一个基底;
⑵若向量在基底下的坐标为,求向量在基底下的坐标.
20.(本小题满分16分)
如图,在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AD上移动.
(1)证明:D1E⊥A1D;
(2)AE等于何值时,二面角D1—EC—D的大小为.
江苏省沭阳高级中学2008-2009学年度第二学期高二单元测试
空间向量参考答案
一、填空题:(本大题共14题,每小题5分,共70 分。)
1、(4) 2、90°3、60° 4、4 5、1 6、60°7、3 8、(-2,)∪(,+∞) 9、 10、
11. 12. 13.③ 14.
二、解答题:本大题共90分,解答应写出文字说明,证明过程和演算步骤。
15. (本小题满分14分)
.法一:综合法证明:连结, ∵,,∴.
又∵,,∴
∴,同理BD1⊥AB1,∵∴BD1⊥面ACB1.
法二: 坐标法证明:先证明BD1⊥AC
∵=++,=+∴ =(+ +) (+)= + = - =||2-||2=0
∴BD1⊥AC,同理可证BD1⊥AB1,∵ 于是BD1⊥平面ACB1
16. . (本小题满分14分)
⑴====,
==
⑵不妨设棱长为1,则,
∴=,,易知
∴异面直线PF与BE所成的角的余弦值为
17. (本小题满分14分)
解:(1)以射线建立坐标系,则B(0,1,0)
18.. (本小题满分16分)
证明:(Ⅰ)作AD的中点O,则VO⊥底面ABCD.建立如图空间直角坐标系,并设正方形边长为1,
则A(,0,0),B(,1,0),C(-,1,0),D(-,0,0),V(0,0,),
∴
由 又AB∩AV=A∴AB⊥平面VAD
(Ⅱ)由(Ⅰ)得是面VAD的法向量,设是面VDB的法向量,则
∴,
又由题意知,面VAD与面VDB所成的二面角,所以其大小为
19. . (本小题满分16分)⑴假设共面,则存在实数使∴,
∴∵∴这不可能.
∴不共面∴也是空间的一个基底.
⑵
20. . (本小题满分16分)解:以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0)C(0,2,0)
(1)
(2)因为E为AB的中点,则E(1,1,0),从而,
,设平面ACD1的法向量为,则
也即,得,从而,所以点E到平面AD1C的距离为
(3)设平面D1EC的法向量,∴
由 令b=1, ∴c=2,a=2-x,
∴
依题意
∴(不合,舍去), .∴AE=时,二面角D1—EC—D的大小为.
PAGE
第 1 页 共 3 页
