【大单元教学】小学数学六下 2.4 圆锥的体积 教案(苏教版)
文档属性
| 名称 | 【大单元教学】小学数学六下 2.4 圆锥的体积 教案(苏教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 570.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《圆柱和圆锥》单元整体教学设计
单元名称 苏教版六年级下册第二单元:《圆柱和圆锥》
课程标准分析 《圆柱与圆锥》单元是图形与几何领域第三学段“图形与几何”中的重要内容。《课程标准》在“内容要求”提出了: 1.通过实例了解圆柱、圆锥体积 (或容积)的意义,知道圆柱、圆锥体积(或容积)的度量单位,能进行单位之间的换算;体验不规则物体体积的测量方法 2.认识圆柱和圆锥,了解圆柱的展开图,探索并掌握圆柱的体积和表面积的计算公式,探索圆锥体积的计算公式,能用这些公式解决生活中的实际问题。 《课程标准》在“学业要求”中指出:认识圆柱和圆锥,能说出圆柱和圆锥的特征,能辨认这些圆柱的展开图,会计算圆柱的体积和表面积;会计算圆锥的体积;能用相应公式解决生活中实际问题。
内容分析 圆柱和圆锥都是平面与曲面围成的立体图形,是在圆的知识与长方体、正方体知识的基础上编排的,通过认识圆柱和圆锥的特征,理解圆柱侧面积和表面积的含义及计算方法,探索并应用圆柱和圆锥的体积计算公式,进一步发展空间观念和思维能力。
单元目标 一、单元目标拟定 1.认识圆柱和圆锥,掌握其特征和几个部分的名称与特点,建立几何模型。 2.认识圆柱的侧面及其展开图,并掌握侧面展开的长方形与圆柱相对应部分的关系。 3.熟练掌握圆柱表面积、圆柱体积、圆锥体积的计算公式,理解圆柱表面积、圆柱、体积、圆锥体积的知识在日常生活中的应用。感受数学知识与实际生活的密切联系,体会学习数学的乐趣。 二、关键内容确定 (一)教学重点 圆柱的表面积、体积的计算;圆锥体积的计算。 (二)教学难点 圆柱的表面积和体积的计算公式的推导;圆锥体积的计算公式的推导;圆柱与圆锥的体积之间的关系。
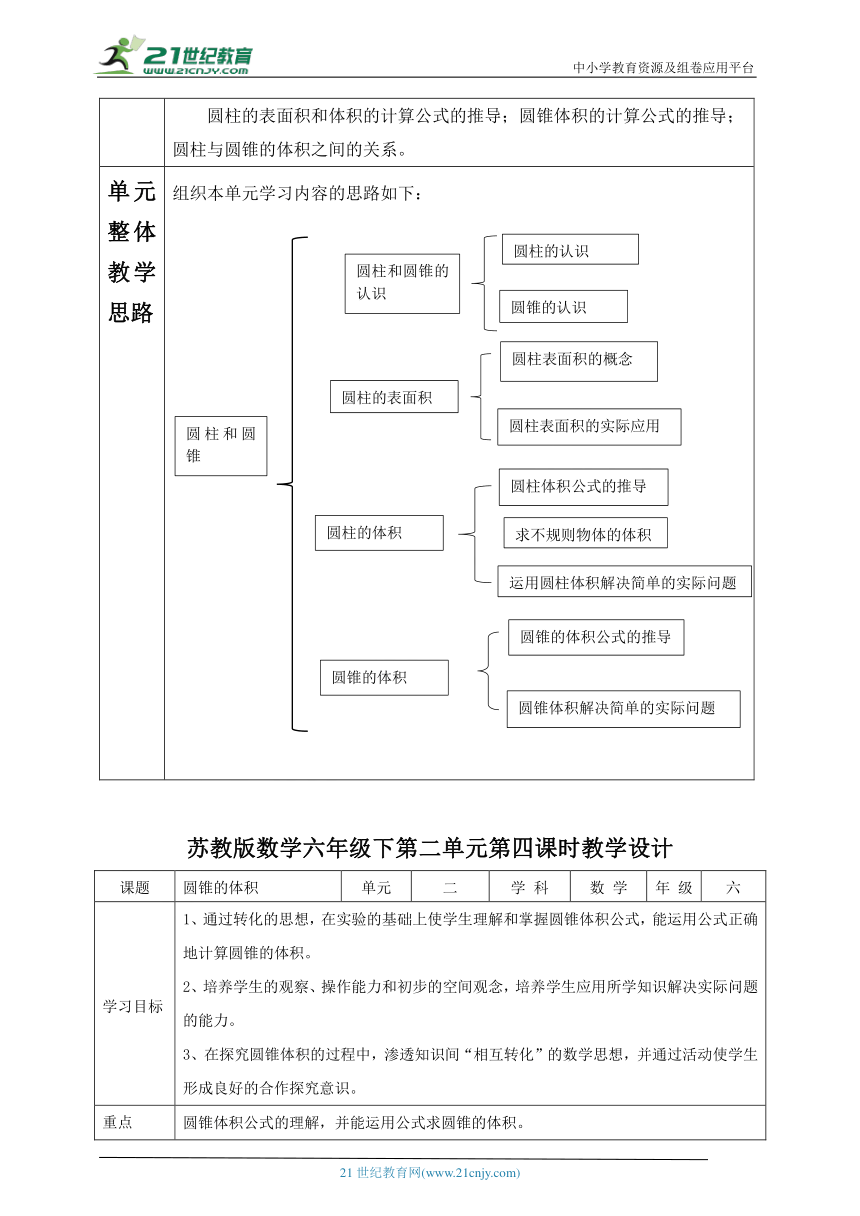
单元整体教学思路 组织本单元学习内容的思路如下:
苏教版数学六年级下第二单元第四课时教学设计
课题 圆锥的体积 单元 二 学 科 数 学 年 级 六
学习目标 1、通过转化的思想,在实验的基础上使学生理解和掌握圆锥体积公式,能运用公式正确地计算圆锥的体积。 2、培养学生的观察、操作能力和初步的空间观念,培养学生应用所学知识解决实际问题的能力。 3、在探究圆锥体积的过程中,渗透知识间“相互转化”的数学思想,并通过活动使学生形成良好的合作探究意识。
重点 圆锥体积公式的理解,并能运用公式求圆锥的体积。
难点 圆锥体积公式的推导。
学情分析 学生以前学习了长方体、正方体,圆柱,对圆锥的特征也有了一定的掌握,且经历了圆柱体积公式的推导过程,初步掌握了“转换”这一数学探究方法,因此在对圆锥的体积探究中,依然让学生多动手操作,进行实践探究,才能有效得出圆锥的体积计算方法。本节中圆锥和以前立体图形的体积不同,以学生现有的知识,无法通过拼割的方法转化成已学过的立体图形,所以引导学生通过实验,利用等底等高这一联系点得出结论成为最主要的方法。
核心素养 发展学生的问题意识,促进数学思维的发展。
教学过程
教学环节 教师活动 学生活动 设计意图
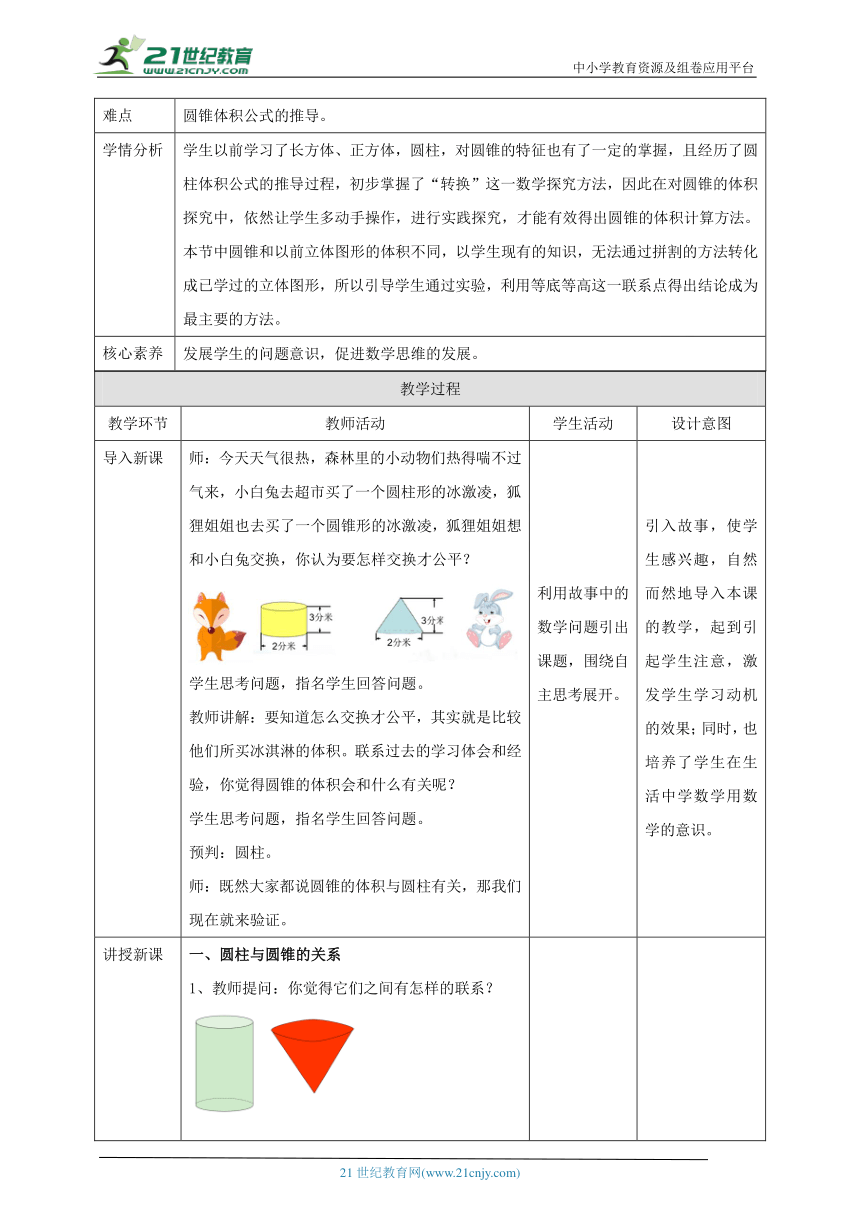
导入新课 师:今天天气很热,森林里的小动物们热得喘不过气来,小白兔去超市买了一个圆柱形的冰激凌,狐狸姐姐也去买了一个圆锥形的冰激凌,狐狸姐姐想和小白兔交换,你认为要怎样交换才公平? 学生思考问题,指名学生回答问题。 教师讲解:要知道怎么交换才公平,其实就是比较他们所买冰淇淋的体积。联系过去的学习体会和经验,你觉得圆锥的体积会和什么有关呢? 学生思考问题,指名学生回答问题。 预判:圆柱。 师:既然大家都说圆锥的体积与圆柱有关,那我们现在就来验证。 利用故事中的数学问题引出课题,围绕自主思考展开。 引入故事,使学生感兴趣,自然而然地导入本课的教学,起到引起学生注意,激发学生学习动机的效果;同时,也培养了学生在生活中学数学用数学的意识。
讲授新课 一、圆柱与圆锥的关系 1、教师提问:你觉得它们之间有怎样的联系? 指名学生回答问题。 预判:不好比较。 教师提问:那你们觉得圆锥的体积该与怎样的圆柱有关呢? 指名学生回答问题。 教师总结:等底等高。 二、验证圆柱与圆锥之间的关系 1、教师提问:下面的圆柱和圆锥底面积相等,高也相等。你能估计出这个圆锥的体积是圆柱的几分之几吗? 学生自主思考,指名学生回答问题。 2、教师提问:你有什么比较好的验证方法吗? 学生自主思考,提出检验的方法。 教师讲解:大家提出了很多可行的方法,我们现在就选择其中的一种方法来进行实验,用倒沙子的方法试一试,看看能得到怎样的结果。 播放幻灯片。 3、完成实验报告 学生自主思考并做题。教师巡视。 邀请学生回答问题。 教师总结: 圆锥的体积V等于和它等底等高的圆柱体积的。 教师提问:计算圆锥的体积所必须的条件可以是什么? 学生自主思考,邀请学生回答问题。 教师讲解: 例题精析 师:通过刚才的学习我们已经知道了计算圆锥体积的计算公式,现在我们一起结合具体的问题,试一试解答计算圆锥的体积吧! 1、一个圆锥形零件,底面积是170平方厘米,高是12厘米。这个零件的体积是多少立方厘米? 学生自主完成题目,并和同桌交流你为什么这么做。教师巡视。 指名学生回答问题。 教师讲解:利用今天所学的公式我们就可以得到我们想要的答案: V=Sh,代入×170×12=680(cm2) 四、课堂练习 1. 一个圆柱和一个圆锥的底面半径的比是1:3,高的比也是1:3,它们的体积之比是( )。 A.1:9 B.1:3 C.9:1 2.把一段底面半径是8分米、高是4分米的圆柱形钢材锻压成底面半径是4分米的圆锥形钢材,它的高是( )分米。 A.48 B.12 C.8 3.有等底等高的圆锥形和圆柱形容器各一个,将圆柱形容器装满水倒入圆锥形容器,当水全部倒完时,从圆锥形容器内溢出36.2 mL水。这时,圆锥形容器内有( )mL水。 A.36.2 B.54.3 C.18.1 4、判断题 (1)圆锥的底面半径扩大3倍,高缩小3 倍后,圆锥的体积不变。( ) (2)求长方体、正方体、圆柱、圆锥的体积,都可以用“底面积×高”来计算。 ( ) (3)一个圆柱形橡皮泥可以做成三个和它等底等高的圆锥。( ) (4)圆锥的高是圆柱的3倍,它们的体积一定相等。( ) (5)一个圆柱形容器中盛满30升水,倒入一个和它等底等高的圆锥形钢材,容器中还剩10升水。( ) 5.求下面组合图形的体积。(单位:厘米,π取3.14) 学生根据老师的问题,进行自主思考。指名学生回答问题。 学生自主思考,指明学生回答问题。 教师讲解,学生认真听讲。 学生完成实验报告,教师巡视。指名学生回答问题,教师总结,学生认真听讲。 教师提问并引导学生思考问题。指明学生回答问题。教师讲解,学生认真听讲。 学生自主完成题目,并和同桌交流。培养团队合作能力。教师总结。学生认真听讲。 通过教师提问,学生自主思考和做题,有利于培养学生的自主思考能力。 运用多媒体技术,形象生动地展示圆柱与圆锥之间的关系。发展了学生的空间观念。 通过自主完成报告,思考和同桌交流。有利于提高思考做题能力以及团队合作能力。教师总结,有利于学生知识的归纳。 教师设疑,有利于引导学生思考。教师总结,有利于学生归纳知识点。
课堂小结 这节课我们学会了什么? 1、圆锥的体积是与它等底等高的圆柱的体积的。 2、圆锥的体积=底面积×高×。 3、已知圆锥的底面积和高,可以利用公式V=Sh直接代入数据计算出圆锥的体积。
板书 圆锥的体积 探究等底等高的圆锥的体积是圆柱体积的几分之几? 1、圆锥的体积是与它等底等高的圆柱的体积的。 2、圆锥的体积=底面积×高×。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《圆柱和圆锥》单元整体教学设计
单元名称 苏教版六年级下册第二单元:《圆柱和圆锥》
课程标准分析 《圆柱与圆锥》单元是图形与几何领域第三学段“图形与几何”中的重要内容。《课程标准》在“内容要求”提出了: 1.通过实例了解圆柱、圆锥体积 (或容积)的意义,知道圆柱、圆锥体积(或容积)的度量单位,能进行单位之间的换算;体验不规则物体体积的测量方法 2.认识圆柱和圆锥,了解圆柱的展开图,探索并掌握圆柱的体积和表面积的计算公式,探索圆锥体积的计算公式,能用这些公式解决生活中的实际问题。 《课程标准》在“学业要求”中指出:认识圆柱和圆锥,能说出圆柱和圆锥的特征,能辨认这些圆柱的展开图,会计算圆柱的体积和表面积;会计算圆锥的体积;能用相应公式解决生活中实际问题。
内容分析 圆柱和圆锥都是平面与曲面围成的立体图形,是在圆的知识与长方体、正方体知识的基础上编排的,通过认识圆柱和圆锥的特征,理解圆柱侧面积和表面积的含义及计算方法,探索并应用圆柱和圆锥的体积计算公式,进一步发展空间观念和思维能力。
单元目标 一、单元目标拟定 1.认识圆柱和圆锥,掌握其特征和几个部分的名称与特点,建立几何模型。 2.认识圆柱的侧面及其展开图,并掌握侧面展开的长方形与圆柱相对应部分的关系。 3.熟练掌握圆柱表面积、圆柱体积、圆锥体积的计算公式,理解圆柱表面积、圆柱、体积、圆锥体积的知识在日常生活中的应用。感受数学知识与实际生活的密切联系,体会学习数学的乐趣。 二、关键内容确定 (一)教学重点 圆柱的表面积、体积的计算;圆锥体积的计算。 (二)教学难点 圆柱的表面积和体积的计算公式的推导;圆锥体积的计算公式的推导;圆柱与圆锥的体积之间的关系。
单元整体教学思路 组织本单元学习内容的思路如下:
苏教版数学六年级下第二单元第四课时教学设计
课题 圆锥的体积 单元 二 学 科 数 学 年 级 六
学习目标 1、通过转化的思想,在实验的基础上使学生理解和掌握圆锥体积公式,能运用公式正确地计算圆锥的体积。 2、培养学生的观察、操作能力和初步的空间观念,培养学生应用所学知识解决实际问题的能力。 3、在探究圆锥体积的过程中,渗透知识间“相互转化”的数学思想,并通过活动使学生形成良好的合作探究意识。
重点 圆锥体积公式的理解,并能运用公式求圆锥的体积。
难点 圆锥体积公式的推导。
学情分析 学生以前学习了长方体、正方体,圆柱,对圆锥的特征也有了一定的掌握,且经历了圆柱体积公式的推导过程,初步掌握了“转换”这一数学探究方法,因此在对圆锥的体积探究中,依然让学生多动手操作,进行实践探究,才能有效得出圆锥的体积计算方法。本节中圆锥和以前立体图形的体积不同,以学生现有的知识,无法通过拼割的方法转化成已学过的立体图形,所以引导学生通过实验,利用等底等高这一联系点得出结论成为最主要的方法。
核心素养 发展学生的问题意识,促进数学思维的发展。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 师:今天天气很热,森林里的小动物们热得喘不过气来,小白兔去超市买了一个圆柱形的冰激凌,狐狸姐姐也去买了一个圆锥形的冰激凌,狐狸姐姐想和小白兔交换,你认为要怎样交换才公平? 学生思考问题,指名学生回答问题。 教师讲解:要知道怎么交换才公平,其实就是比较他们所买冰淇淋的体积。联系过去的学习体会和经验,你觉得圆锥的体积会和什么有关呢? 学生思考问题,指名学生回答问题。 预判:圆柱。 师:既然大家都说圆锥的体积与圆柱有关,那我们现在就来验证。 利用故事中的数学问题引出课题,围绕自主思考展开。 引入故事,使学生感兴趣,自然而然地导入本课的教学,起到引起学生注意,激发学生学习动机的效果;同时,也培养了学生在生活中学数学用数学的意识。
讲授新课 一、圆柱与圆锥的关系 1、教师提问:你觉得它们之间有怎样的联系? 指名学生回答问题。 预判:不好比较。 教师提问:那你们觉得圆锥的体积该与怎样的圆柱有关呢? 指名学生回答问题。 教师总结:等底等高。 二、验证圆柱与圆锥之间的关系 1、教师提问:下面的圆柱和圆锥底面积相等,高也相等。你能估计出这个圆锥的体积是圆柱的几分之几吗? 学生自主思考,指名学生回答问题。 2、教师提问:你有什么比较好的验证方法吗? 学生自主思考,提出检验的方法。 教师讲解:大家提出了很多可行的方法,我们现在就选择其中的一种方法来进行实验,用倒沙子的方法试一试,看看能得到怎样的结果。 播放幻灯片。 3、完成实验报告 学生自主思考并做题。教师巡视。 邀请学生回答问题。 教师总结: 圆锥的体积V等于和它等底等高的圆柱体积的。 教师提问:计算圆锥的体积所必须的条件可以是什么? 学生自主思考,邀请学生回答问题。 教师讲解: 例题精析 师:通过刚才的学习我们已经知道了计算圆锥体积的计算公式,现在我们一起结合具体的问题,试一试解答计算圆锥的体积吧! 1、一个圆锥形零件,底面积是170平方厘米,高是12厘米。这个零件的体积是多少立方厘米? 学生自主完成题目,并和同桌交流你为什么这么做。教师巡视。 指名学生回答问题。 教师讲解:利用今天所学的公式我们就可以得到我们想要的答案: V=Sh,代入×170×12=680(cm2) 四、课堂练习 1. 一个圆柱和一个圆锥的底面半径的比是1:3,高的比也是1:3,它们的体积之比是( )。 A.1:9 B.1:3 C.9:1 2.把一段底面半径是8分米、高是4分米的圆柱形钢材锻压成底面半径是4分米的圆锥形钢材,它的高是( )分米。 A.48 B.12 C.8 3.有等底等高的圆锥形和圆柱形容器各一个,将圆柱形容器装满水倒入圆锥形容器,当水全部倒完时,从圆锥形容器内溢出36.2 mL水。这时,圆锥形容器内有( )mL水。 A.36.2 B.54.3 C.18.1 4、判断题 (1)圆锥的底面半径扩大3倍,高缩小3 倍后,圆锥的体积不变。( ) (2)求长方体、正方体、圆柱、圆锥的体积,都可以用“底面积×高”来计算。 ( ) (3)一个圆柱形橡皮泥可以做成三个和它等底等高的圆锥。( ) (4)圆锥的高是圆柱的3倍,它们的体积一定相等。( ) (5)一个圆柱形容器中盛满30升水,倒入一个和它等底等高的圆锥形钢材,容器中还剩10升水。( ) 5.求下面组合图形的体积。(单位:厘米,π取3.14) 学生根据老师的问题,进行自主思考。指名学生回答问题。 学生自主思考,指明学生回答问题。 教师讲解,学生认真听讲。 学生完成实验报告,教师巡视。指名学生回答问题,教师总结,学生认真听讲。 教师提问并引导学生思考问题。指明学生回答问题。教师讲解,学生认真听讲。 学生自主完成题目,并和同桌交流。培养团队合作能力。教师总结。学生认真听讲。 通过教师提问,学生自主思考和做题,有利于培养学生的自主思考能力。 运用多媒体技术,形象生动地展示圆柱与圆锥之间的关系。发展了学生的空间观念。 通过自主完成报告,思考和同桌交流。有利于提高思考做题能力以及团队合作能力。教师总结,有利于学生知识的归纳。 教师设疑,有利于引导学生思考。教师总结,有利于学生归纳知识点。
课堂小结 这节课我们学会了什么? 1、圆锥的体积是与它等底等高的圆柱的体积的。 2、圆锥的体积=底面积×高×。 3、已知圆锥的底面积和高,可以利用公式V=Sh直接代入数据计算出圆锥的体积。
板书 圆锥的体积 探究等底等高的圆锥的体积是圆柱体积的几分之几? 1、圆锥的体积是与它等底等高的圆柱的体积的。 2、圆锥的体积=底面积×高×。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
