北师大版数学必修2 第一章 立体几何初步 综合能力检测
文档属性
| 名称 | 北师大版数学必修2 第一章 立体几何初步 综合能力检测 |  | |
| 格式 | zip | ||
| 文件大小 | 318.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-27 07:01:48 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第一章综合能力检测
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)【来源:21·世纪·教育·网】
1. 若P是平面α外一点,则下列命题正确的是( )
A.过P只能作一条直线与平面α相交
B.过P可作无数条直线与平面α垂直
C.过P只能作一条直线与平面α平行
D.过P可作无数条直线与平面α平行
[答案] D
[解析] 过P点平行于α的平面内任一直线都与平面α平行.
2.一条直线若同时平行于两个相交平面,那么这条直线与这两个平面的交线的位置关系是( )
A.异面 B.相交
C.平行 D.不能确定
[答案] C
[解析] 如图所示,设α∩β=l,a∥α,a∥β,过直线a作与α,β都相交的平面γ.
记α∩γ=b,β∩γ=c,
则a∥b,且a∥c,
所以b∥c,b∥β.
又b?α,α∩β=l,
所以b∥l,a∥l.
3.(广东高考)设l为直线,α,β是两个不同的平面.下列命题中正确的是( )
A.若l∥α,l∥β,则α∥β
B.若l⊥α,l⊥β,则α∥β
C.若l⊥α,l∥β,则α∥β
D.若l⊥β,l∥α,则l⊥β
[答案] B
[解析] 本题考查了空间线面关系.
若α∩β=m,l∥m,lα,lβ,则A错.
垂直于同一直线的两平面平行,B正确.
当l⊥α,l∥β时α⊥β,C错.
若α⊥β,l∥α,则l与β关系不确定,D错.
4.两个半径为1的小铁球,熔化后铸成一个大球,这个大球的半径为( )
A.2 B.
C. D.
[答案] B
[解析] 熔化后铸成的大球的体积等于两个小铁球的体积之和.设大球的半径为R,则πR3=2×π×13,所以R=.故选B.2-1-c-n-j-y
5.某三棱锥的左视图、俯视图如图所示,则该三棱锥的体积是( )
(锥体体积公式:V=Sh,其中S为底面面积,h为高)
A.3 B.2
C. D.1
[答案] D
[解析] 本题考查了三视图及体积计算公式 ( http: / / www.21cnjy.com )等.由图知平面PAB⊥平面ABC,PD⊥AB,PD⊥平面ABC,底面是边长为2的正三角形,∴V=Sh=××=1.由三视图找出垂直关系是关键.【来源:21cnj*y.co*m】
6.(2015·山东高考)在梯形ABCD中 ( http: / / www.21cnjy.com ),∠ABC=,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A. B.
C. D.2π
[答案] C
[解析] 梯形ABCD绕AD所在直线旋转一 ( http: / / www.21cnjy.com )周所形成的曲面所围成的几何体是一个底面半径为1,高为2的圆柱挖去一个底面半径为1,高为1的圆锥所得的组合体;所以该组合体的体积为V=V圆柱-V圆锥=π×12×2-π×12×1=2π-=.故选C.
7.平面α与平面β平行的条件可以是( )
A.α内有无穷多条直线与β平行
B.直线a∥α,a∥β
C.直线a?α,直线b?β,且a∥β,b∥α
D.α内的任何直线都与β平行
[答案] D
[解析] 选项A有可能平行,也有可能相交;选项B、C,平面α与平面β可能相交;选项D正确.
8.如图,BCDE是一个正方形,AB⊥平面BCDE,则图中(侧面,底面)互相垂直的平面共有( )
A.4组 B.5组
C.6组 D.7组
[答案] B
[解析] 与平面BCDE垂 ( http: / / www.21cnjy.com )直的平面有2个,与平面ABC垂直的平面有2个,(含平面ABE,不含平面BCDE).与平面ABE垂直的平面有2个(含平面ABC,不含平面BCDE),∴2+2+2-1=5.【出处:21教育名师】
9.有相等表面积的球及正方体,它们的体积记为V球和V正,球的直径为d,正方体的棱长为a,则( )
A.d>a,V球>V正 B.d>a,V球C.dV正 D.d[答案] A
[解析] S球面=4πr2=6a2=S正方体,
∴=,=>1,∴d>a.
V球︰V正=πr3︰a3=πd3︰6a3=d︰a,
∴V球>V正.
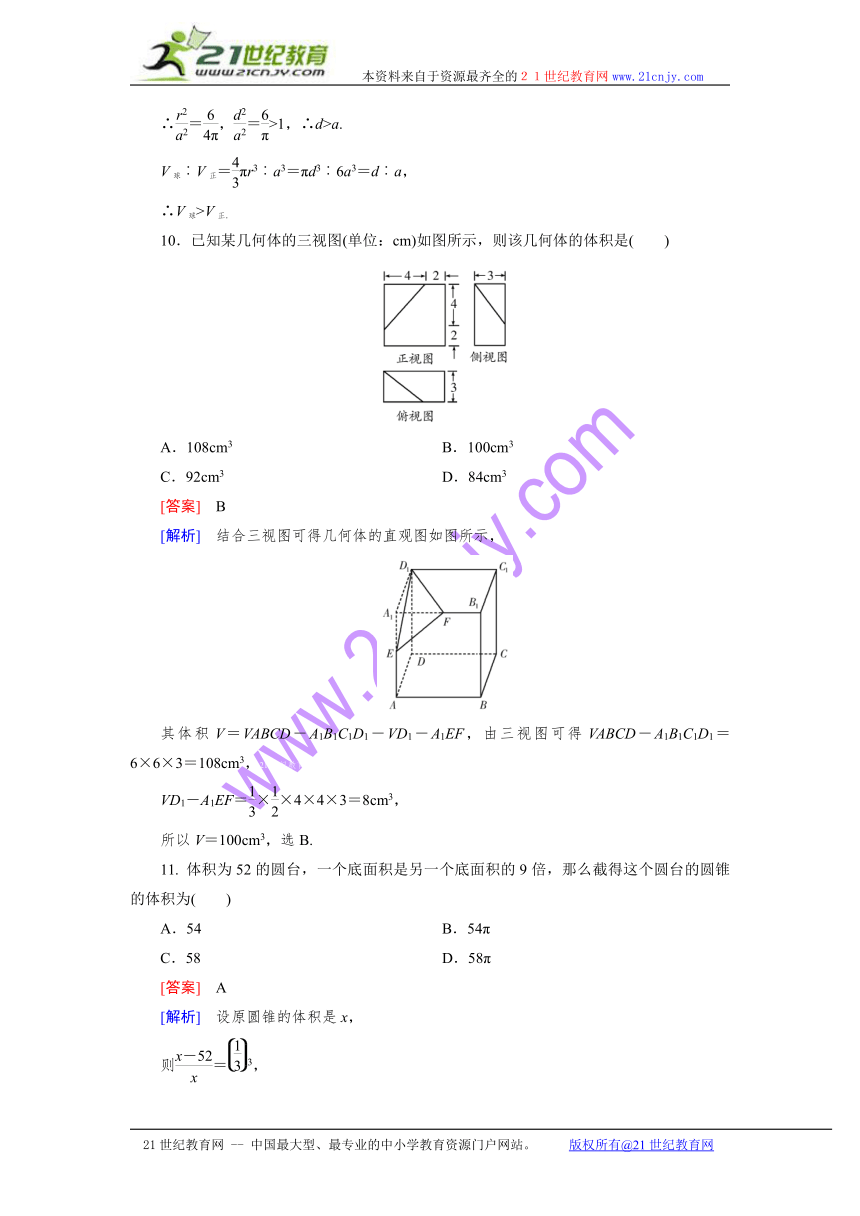
10.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
A.108cm3 B.100cm3
C.92cm3 D.84cm3
[答案] B
[解析] 结合三视图可得几何体的直观图如图所示,
其体积V=VABCD-A1B1C1D1-VD1-A1EF,由三视图可得VABCD-A1B1C1D1=6×6×3=108cm3,21世纪教育网版权所有
VD1-A1EF=××4×4×3=8cm3,
所以V=100cm3,选B.
11. 体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积为( )
A.54 B.54π
C.58 D.58π
[答案] A
[解析] 设原圆锥的体积是x,
则=3,
∴x=54.
12.如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=,则下列结论中错误的是( )21cnjy.com
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
[答案] D
[解析] 本题主要考查线线垂直、线面平行、三棱锥的体积等知识,考查学生的推理论证能力.
对于选项A,由正方体ABCD-A1B1C1D1得B1B⊥面AC,∴AC⊥B1B,
又∵AC⊥BD,
∴AC⊥面BDD1B1,BE?面BDD1B1,
∴AC⊥BE.
对于选项B,由正方体ABCD-A1B1C1D1得B1D1∥BD,
B1D1面ABCD,BD?面ABCD,
∴B1D1∥面ABCD,∴EF∥面ABCD.
对于选项C,VA-BEF=×××1×=.
∴三棱锥A-BEF的体积为定值.
对于选项D,因线段B1D1上两个动点E,F,且EF=,
在E,F移动时,A到EF的距离与B到EF的距离不相等
∴△AEF的面积与△BEF的面积不相等.
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在题中横线上)
13.如下图中的三个直角三角形是一个体积20cm3的几何体的三视图,则h=________ cm.
[答案] 4
[解析] 该几何体是一个底面是直角三角形,一条侧棱垂直于底面的三棱锥如图,V=××h=20,∴h=4 cm.21教育网
14.若圆锥的侧面积为2π,底面面积为π,则该圆锥的体积为________.
[答案]
[解析] 设圆锥的母线为l,底面半径为r,高为h,由得所以h==.于是,圆锥的体积为V=πr2h=.21·cn·jy·com
15.如图所示,正三棱柱ABC—A1B1C1的底面边长为2,侧棱长为4,E,F分别是AB,A1C1的中点,则EF的长等于________.21·世纪*教育网
[答案]
[解析] 取A1B1的中点H,连接EH,FH,则EH=4,FH=1.
由正三棱柱的性质知△EFH为直角三角形.
所以EF==.
16.若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则________(写出所有正确结论的编号). 21*cnjy*com
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等;
③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°;
④连接四面体ABCD每组对棱中点的线段相互垂直平分;
⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.
[答案] ②④⑤
[解析] 本题考查了空间几何体中点线面的位置关系.
依题意,该四面体可看作是一个长方体截掉 ( http: / / www.21cnjy.com )四个顶角后剩余部分,所以可以确定②④⑤正确.对于①,只有四面体ABCD是正四面体时才成立.对于③,取特例正四面体知夹角和为60°+60°+60°=180°知③错.【版权所有:21教育】
三、解答题(本大题共6个小题,满分70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)如图是一个几何体的主视图和俯视图.
(1)试判断这个几何体是什么几何体;
(2)请画出它的左视图,并求该左视图的面积.
[解析] (1)由题图中的主视图和俯视图知该几何体是正六棱锥.
(2)该几何体的左视图如图所示.
其中两腰为斜高,底边长为a,三角形的高即为正六棱锥的高,且长为a.
所以该左视图的面积为a·a=a2.
18.(本小题满分12分)如图,棱柱ABC-A1B1C1的侧面BCC1B1是菱形,B1C⊥A1B.
(1)证明:平面AB1C⊥平面A1BC1;
(2)设D是A1C1上的点,且A1B∥平面B1CD,求A1D︰DC1的值.
[解析] (1)∵侧面BCC1B1是菱形,∴B1C⊥BC1,
又∵B1C⊥A1B,且A1B∩BC1=B,
∴B1C⊥平面A1BC1,
又B1C?平面AB1C
∴平面AB1C⊥平面A1BC1 .
(2)设BC1交B1C于点E,连接DE,
则DE是平面A1BC1与平面B1CD的交线.
∵A1B∥平面B1CD,A1B?平面A1BC1,
平面A1BC1∩平面B1CD=DE,∴A1B∥DE.
又E是BC1的中点,∴D为A1C1的中点.
即A1D︰DC1=1.
19.(本小题满分12分)(201 ( http: / / www.21cnjy.com )5·广东高考)如图所示,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.21教育名师原创作品
(1)证明:BC∥平面PDA;
(2)证明:BC⊥PD;
(3)求点C到平面PDA的距离.
[解析] (1)因为四边形ABCD是长方形,所以BC∥AD,因为BC平面PDA,AD?平面PDA,所以BC∥平面PDA.21*cnjy*com
(2)因为四边形ABCD是长方形,
所以BC⊥CD,
因为平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,BC?平面ABCD,
所以BC⊥平面PDC,
因为PD?平面PDC,
所以BC⊥PD.
(3)取CD的中点E,连接AE和PE,
因为PD=PC,所以PE⊥CD,
在Rt△PED中,PE===,
因为平面PDC⊥平面ABCD,平面 ( http: / / www.21cnjy.com )PDC∩平面ABCD=CD,PE?平面PDC,所以PE⊥平面ABCD,由(2)知:BC⊥平面PDC,由(1)知:BC∥AD,
所以AD⊥平面PDC,
因为PD?平面PDC,所以AD⊥PD,
设点C到平面PDA的距离为h,因为V三棱锥C-PDA=V三棱锥P-ACD,所以S△PDA·h=S△ACD·PE,即h===,
所以点C到平面PDA的距离是.
20.(本小题满分12分)如图,四棱锥P-A ( http: / / www.21cnjy.com )BCD的底面边长为8的正方形,四条侧棱长均为2.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
(1)证明: GH∥EF;
(2)若EB=2,求四边形GEFH的面积.
[解析] (1)∵BC∥平面GEFH,BC?平面PBC,且平面PBC∩平面GEFH=GH,
∴GH∥BC.
同理可证EF∥BC,∴GH∥EF.
(2)连接AC,BD交于一点O,BD交EF于K,连接OP、GK.
因为PA=PC,O是AC的中点,所以PO⊥AC,
同理可证PO⊥BD,
又∵BD∩AC=O,且AC,BD都在底面内,
∴PO⊥平面ABCD,
又∵平面GEFH⊥平面ABCD,PO 平面GEFH,
∴PO∥平面GEFH.
又∵平面GEFH∩平面PBD=GK,
∴PO∥GK,且GK⊥平面ABCD,
∴GK⊥EF,
所以GK是梯形GEFH的高.
∵AB=8,EB=2,
∴EB︰AB=KB︰DB=1︰4,
∴KB=DB=OB,即K为OB的中点,
又∵PO∥GK,
∴GK=PO,即G是PB的中点,且GH=BC=4.
又由已知得OB=4,PO===6.
∴GK=3.
∴四边形GEFH的面积S=·GK=×3=18.
21.(本小题满分12分) ( http: / / www.21cnjy.com )(北京高考)如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD、PC的中点,求证:
(1)PA⊥底面ABCD;
(2)BE∥平面PAD;
(3)平面BEF⊥平面PCD.
[解析] (1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.
(2)因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE.
所以四边形ABED为平行四边形.所以BE∥AD.
又因为BE平面PAD,AD?平面PAD,
所以BE∥平面PAD.
(3)因为AB⊥AD,而且ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD.所以PA⊥CD.
所以CD⊥平面PAD.所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PD∥EF.所以CD⊥EF,
又因为CD⊥BE,BE∩EF=E,
所以CD⊥平面BEF. 所以平面BEF⊥平面PCD.
22.(本小题满分12分)正三棱锥高为1,底面边长为2,内有一球与四个面都相切.
(1)求棱锥的全面积;
(2)求球的半径及表面积.
[解析] (1)设底面中心为O,D为AB中点,则VD为斜高,OD=AB=,在Rt△VOD中,VO=1,VD==.www.21-cn-jy.com
∴S全=(2)2+3×2××=6+9.
(2)解法一:设球的半径为R,由△VO1E∽△VDO有= = R=-2,
故S球=4πR2=4π(-2)2=8(5-2)π.
解法二:VV-ABC=S△ABC·h=(S△ABC+S△VAB+S△VCB+S△VAC)R,而S△ABC=·(2)2=6.2·1·c·n·j·y
S△VAB+S△VCB+S△VAC=3S△VAB=3··2·=9.故6·1=(6+9)R R=-2,www-2-1-cnjy-com
故S球=4πR2=4π(-2)2=8(5-2)π.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第一章综合能力检测
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)【来源:21·世纪·教育·网】
1. 若P是平面α外一点,则下列命题正确的是( )
A.过P只能作一条直线与平面α相交
B.过P可作无数条直线与平面α垂直
C.过P只能作一条直线与平面α平行
D.过P可作无数条直线与平面α平行
[答案] D
[解析] 过P点平行于α的平面内任一直线都与平面α平行.
2.一条直线若同时平行于两个相交平面,那么这条直线与这两个平面的交线的位置关系是( )
A.异面 B.相交
C.平行 D.不能确定
[答案] C
[解析] 如图所示,设α∩β=l,a∥α,a∥β,过直线a作与α,β都相交的平面γ.
记α∩γ=b,β∩γ=c,
则a∥b,且a∥c,
所以b∥c,b∥β.
又b?α,α∩β=l,
所以b∥l,a∥l.
3.(广东高考)设l为直线,α,β是两个不同的平面.下列命题中正确的是( )
A.若l∥α,l∥β,则α∥β
B.若l⊥α,l⊥β,则α∥β
C.若l⊥α,l∥β,则α∥β
D.若l⊥β,l∥α,则l⊥β
[答案] B
[解析] 本题考查了空间线面关系.
若α∩β=m,l∥m,lα,lβ,则A错.
垂直于同一直线的两平面平行,B正确.
当l⊥α,l∥β时α⊥β,C错.
若α⊥β,l∥α,则l与β关系不确定,D错.
4.两个半径为1的小铁球,熔化后铸成一个大球,这个大球的半径为( )
A.2 B.
C. D.
[答案] B
[解析] 熔化后铸成的大球的体积等于两个小铁球的体积之和.设大球的半径为R,则πR3=2×π×13,所以R=.故选B.2-1-c-n-j-y
5.某三棱锥的左视图、俯视图如图所示,则该三棱锥的体积是( )
(锥体体积公式:V=Sh,其中S为底面面积,h为高)
A.3 B.2
C. D.1
[答案] D
[解析] 本题考查了三视图及体积计算公式 ( http: / / www.21cnjy.com )等.由图知平面PAB⊥平面ABC,PD⊥AB,PD⊥平面ABC,底面是边长为2的正三角形,∴V=Sh=××=1.由三视图找出垂直关系是关键.【来源:21cnj*y.co*m】
6.(2015·山东高考)在梯形ABCD中 ( http: / / www.21cnjy.com ),∠ABC=,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A. B.
C. D.2π
[答案] C
[解析] 梯形ABCD绕AD所在直线旋转一 ( http: / / www.21cnjy.com )周所形成的曲面所围成的几何体是一个底面半径为1,高为2的圆柱挖去一个底面半径为1,高为1的圆锥所得的组合体;所以该组合体的体积为V=V圆柱-V圆锥=π×12×2-π×12×1=2π-=.故选C.
7.平面α与平面β平行的条件可以是( )
A.α内有无穷多条直线与β平行
B.直线a∥α,a∥β
C.直线a?α,直线b?β,且a∥β,b∥α
D.α内的任何直线都与β平行
[答案] D
[解析] 选项A有可能平行,也有可能相交;选项B、C,平面α与平面β可能相交;选项D正确.
8.如图,BCDE是一个正方形,AB⊥平面BCDE,则图中(侧面,底面)互相垂直的平面共有( )
A.4组 B.5组
C.6组 D.7组
[答案] B
[解析] 与平面BCDE垂 ( http: / / www.21cnjy.com )直的平面有2个,与平面ABC垂直的平面有2个,(含平面ABE,不含平面BCDE).与平面ABE垂直的平面有2个(含平面ABC,不含平面BCDE),∴2+2+2-1=5.【出处:21教育名师】
9.有相等表面积的球及正方体,它们的体积记为V球和V正,球的直径为d,正方体的棱长为a,则( )
A.d>a,V球>V正 B.d>a,V球
[解析] S球面=4πr2=6a2=S正方体,
∴=,=>1,∴d>a.
V球︰V正=πr3︰a3=πd3︰6a3=d︰a,
∴V球>V正.
10.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
A.108cm3 B.100cm3
C.92cm3 D.84cm3
[答案] B
[解析] 结合三视图可得几何体的直观图如图所示,
其体积V=VABCD-A1B1C1D1-VD1-A1EF,由三视图可得VABCD-A1B1C1D1=6×6×3=108cm3,21世纪教育网版权所有
VD1-A1EF=××4×4×3=8cm3,
所以V=100cm3,选B.
11. 体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积为( )
A.54 B.54π
C.58 D.58π
[答案] A
[解析] 设原圆锥的体积是x,
则=3,
∴x=54.
12.如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=,则下列结论中错误的是( )21cnjy.com
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.△AEF的面积与△BEF的面积相等
[答案] D
[解析] 本题主要考查线线垂直、线面平行、三棱锥的体积等知识,考查学生的推理论证能力.
对于选项A,由正方体ABCD-A1B1C1D1得B1B⊥面AC,∴AC⊥B1B,
又∵AC⊥BD,
∴AC⊥面BDD1B1,BE?面BDD1B1,
∴AC⊥BE.
对于选项B,由正方体ABCD-A1B1C1D1得B1D1∥BD,
B1D1面ABCD,BD?面ABCD,
∴B1D1∥面ABCD,∴EF∥面ABCD.
对于选项C,VA-BEF=×××1×=.
∴三棱锥A-BEF的体积为定值.
对于选项D,因线段B1D1上两个动点E,F,且EF=,
在E,F移动时,A到EF的距离与B到EF的距离不相等
∴△AEF的面积与△BEF的面积不相等.
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在题中横线上)
13.如下图中的三个直角三角形是一个体积20cm3的几何体的三视图,则h=________ cm.
[答案] 4
[解析] 该几何体是一个底面是直角三角形,一条侧棱垂直于底面的三棱锥如图,V=××h=20,∴h=4 cm.21教育网
14.若圆锥的侧面积为2π,底面面积为π,则该圆锥的体积为________.
[答案]
[解析] 设圆锥的母线为l,底面半径为r,高为h,由得所以h==.于是,圆锥的体积为V=πr2h=.21·cn·jy·com
15.如图所示,正三棱柱ABC—A1B1C1的底面边长为2,侧棱长为4,E,F分别是AB,A1C1的中点,则EF的长等于________.21·世纪*教育网
[答案]
[解析] 取A1B1的中点H,连接EH,FH,则EH=4,FH=1.
由正三棱柱的性质知△EFH为直角三角形.
所以EF==.
16.若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则________(写出所有正确结论的编号). 21*cnjy*com
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等;
③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°;
④连接四面体ABCD每组对棱中点的线段相互垂直平分;
⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.
[答案] ②④⑤
[解析] 本题考查了空间几何体中点线面的位置关系.
依题意,该四面体可看作是一个长方体截掉 ( http: / / www.21cnjy.com )四个顶角后剩余部分,所以可以确定②④⑤正确.对于①,只有四面体ABCD是正四面体时才成立.对于③,取特例正四面体知夹角和为60°+60°+60°=180°知③错.【版权所有:21教育】
三、解答题(本大题共6个小题,满分70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)如图是一个几何体的主视图和俯视图.
(1)试判断这个几何体是什么几何体;
(2)请画出它的左视图,并求该左视图的面积.
[解析] (1)由题图中的主视图和俯视图知该几何体是正六棱锥.
(2)该几何体的左视图如图所示.
其中两腰为斜高,底边长为a,三角形的高即为正六棱锥的高,且长为a.
所以该左视图的面积为a·a=a2.
18.(本小题满分12分)如图,棱柱ABC-A1B1C1的侧面BCC1B1是菱形,B1C⊥A1B.
(1)证明:平面AB1C⊥平面A1BC1;
(2)设D是A1C1上的点,且A1B∥平面B1CD,求A1D︰DC1的值.
[解析] (1)∵侧面BCC1B1是菱形,∴B1C⊥BC1,
又∵B1C⊥A1B,且A1B∩BC1=B,
∴B1C⊥平面A1BC1,
又B1C?平面AB1C
∴平面AB1C⊥平面A1BC1 .
(2)设BC1交B1C于点E,连接DE,
则DE是平面A1BC1与平面B1CD的交线.
∵A1B∥平面B1CD,A1B?平面A1BC1,
平面A1BC1∩平面B1CD=DE,∴A1B∥DE.
又E是BC1的中点,∴D为A1C1的中点.
即A1D︰DC1=1.
19.(本小题满分12分)(201 ( http: / / www.21cnjy.com )5·广东高考)如图所示,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.21教育名师原创作品
(1)证明:BC∥平面PDA;
(2)证明:BC⊥PD;
(3)求点C到平面PDA的距离.
[解析] (1)因为四边形ABCD是长方形,所以BC∥AD,因为BC平面PDA,AD?平面PDA,所以BC∥平面PDA.21*cnjy*com
(2)因为四边形ABCD是长方形,
所以BC⊥CD,
因为平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,BC?平面ABCD,
所以BC⊥平面PDC,
因为PD?平面PDC,
所以BC⊥PD.
(3)取CD的中点E,连接AE和PE,
因为PD=PC,所以PE⊥CD,
在Rt△PED中,PE===,
因为平面PDC⊥平面ABCD,平面 ( http: / / www.21cnjy.com )PDC∩平面ABCD=CD,PE?平面PDC,所以PE⊥平面ABCD,由(2)知:BC⊥平面PDC,由(1)知:BC∥AD,
所以AD⊥平面PDC,
因为PD?平面PDC,所以AD⊥PD,
设点C到平面PDA的距离为h,因为V三棱锥C-PDA=V三棱锥P-ACD,所以S△PDA·h=S△ACD·PE,即h===,
所以点C到平面PDA的距离是.
20.(本小题满分12分)如图,四棱锥P-A ( http: / / www.21cnjy.com )BCD的底面边长为8的正方形,四条侧棱长均为2.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
(1)证明: GH∥EF;
(2)若EB=2,求四边形GEFH的面积.
[解析] (1)∵BC∥平面GEFH,BC?平面PBC,且平面PBC∩平面GEFH=GH,
∴GH∥BC.
同理可证EF∥BC,∴GH∥EF.
(2)连接AC,BD交于一点O,BD交EF于K,连接OP、GK.
因为PA=PC,O是AC的中点,所以PO⊥AC,
同理可证PO⊥BD,
又∵BD∩AC=O,且AC,BD都在底面内,
∴PO⊥平面ABCD,
又∵平面GEFH⊥平面ABCD,PO 平面GEFH,
∴PO∥平面GEFH.
又∵平面GEFH∩平面PBD=GK,
∴PO∥GK,且GK⊥平面ABCD,
∴GK⊥EF,
所以GK是梯形GEFH的高.
∵AB=8,EB=2,
∴EB︰AB=KB︰DB=1︰4,
∴KB=DB=OB,即K为OB的中点,
又∵PO∥GK,
∴GK=PO,即G是PB的中点,且GH=BC=4.
又由已知得OB=4,PO===6.
∴GK=3.
∴四边形GEFH的面积S=·GK=×3=18.
21.(本小题满分12分) ( http: / / www.21cnjy.com )(北京高考)如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD、PC的中点,求证:
(1)PA⊥底面ABCD;
(2)BE∥平面PAD;
(3)平面BEF⊥平面PCD.
[解析] (1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.
(2)因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE.
所以四边形ABED为平行四边形.所以BE∥AD.
又因为BE平面PAD,AD?平面PAD,
所以BE∥平面PAD.
(3)因为AB⊥AD,而且ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD.所以PA⊥CD.
所以CD⊥平面PAD.所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PD∥EF.所以CD⊥EF,
又因为CD⊥BE,BE∩EF=E,
所以CD⊥平面BEF. 所以平面BEF⊥平面PCD.
22.(本小题满分12分)正三棱锥高为1,底面边长为2,内有一球与四个面都相切.
(1)求棱锥的全面积;
(2)求球的半径及表面积.
[解析] (1)设底面中心为O,D为AB中点,则VD为斜高,OD=AB=,在Rt△VOD中,VO=1,VD==.www.21-cn-jy.com
∴S全=(2)2+3×2××=6+9.
(2)解法一:设球的半径为R,由△VO1E∽△VDO有= = R=-2,
故S球=4πR2=4π(-2)2=8(5-2)π.
解法二:VV-ABC=S△ABC·h=(S△ABC+S△VAB+S△VCB+S△VAC)R,而S△ABC=·(2)2=6.2·1·c·n·j·y
S△VAB+S△VCB+S△VAC=3S△VAB=3··2·=9.故6·1=(6+9)R R=-2,www-2-1-cnjy-com
故S球=4πR2=4π(-2)2=8(5-2)π.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
