2015年北师大版数学必修2 综合测试试题(B)
文档属性
| 名称 | 2015年北师大版数学必修2 综合测试试题(B) |

|
|
| 格式 | zip | ||
| 文件大小 | 246.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-27 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
本册综合测试二
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)21教育网
1.若空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2∥l3,l3⊥l4,则下列结论一定正确的是( )21cnjy.com
A.l1⊥l4
B.l1∥l4
C.l1与l4既不垂直也不平行
D.l1与l4的位置关系不确定
[答案] D
[解析] 本题考查空间中的平行关系.
通过作图可知l1与l4的位置关系不确定,选D,动手作试验是解决本题的好方法.
2. 直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,则m的值为( )
A.2 B.-3
C.2或-3 D.-2或-3
[答案] C
[解析] 解法1:l1:2x+(m+1)y+4=0,
l2:mx+3y-2=0,
当m=0时,显然l1不平行于l2;
当m≠0时,若l1∥l2,需=≠.①
由①式有m2+m-6=0,解得m=2,或m=-3.
显然m=2,或m=-3满足①.∴应选C.
解法2:若l1∥l2,需2×3-m(m+1)=0,解得m=-3,或m=2.
当m=-3或2时,A1C2-A2C1=2×(-2)-m·4=-4-4m≠0.
∴m=-3或2为所求.∴应选C.
3. 若a,b是异面直线,b,c是异面直线,则a,c的位置关系为( )
A.相交、平行或异面 B.相交或平行
C.异面 D.平行或异面
[答案] A
[解析] a与c可以相交、平行或异面,分别如下图中的(1),(2),(3).
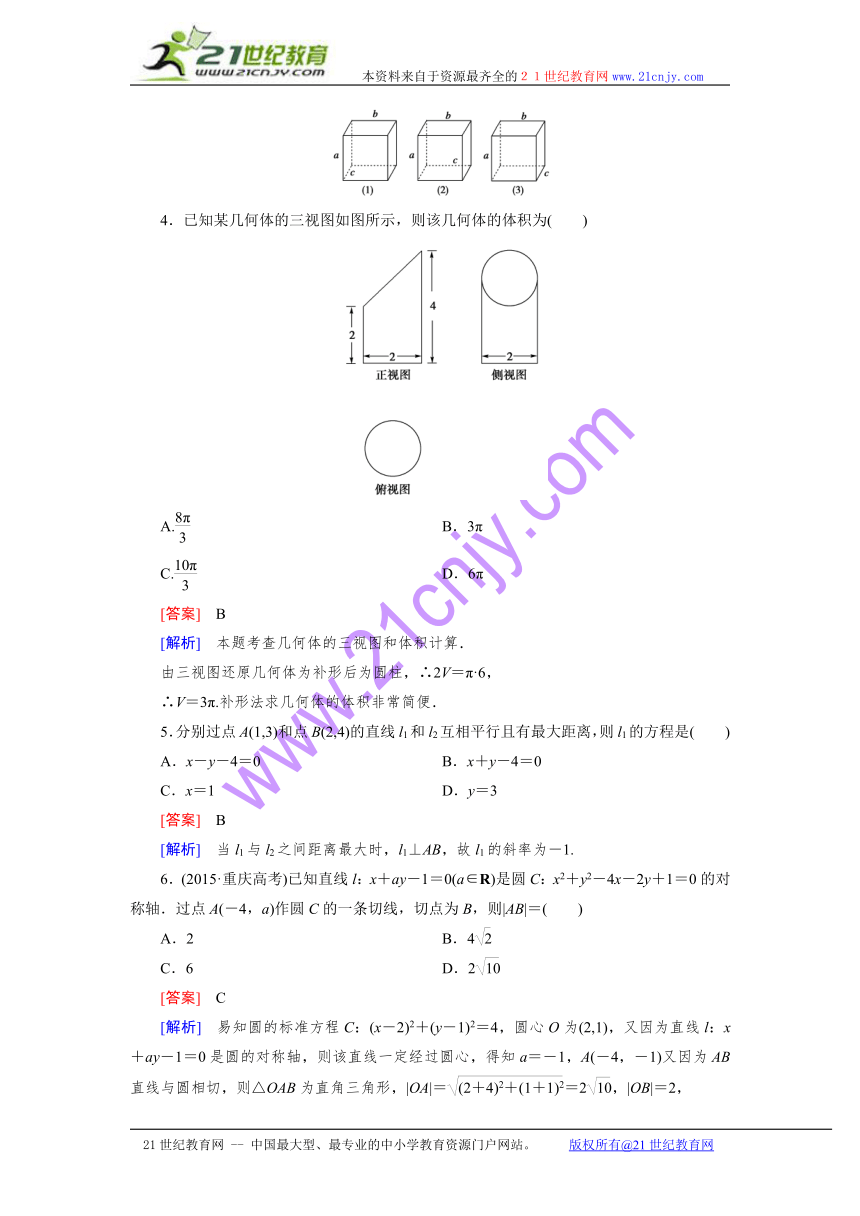
4.已知某几何体的三视图如图所示,则该几何体的体积为( )
A. B.3π
C. D.6π
[答案] B
[解析] 本题考查几何体的三视图和体积计算.
由三视图还原几何体为补形后为圆柱,∴2V=π·6,
∴V=3π.补形法求几何体的体积非常简便.
5.分别过点A(1,3)和点B(2,4)的直线l1和l2互相平行且有最大距离,则l1的方程是( )
A.x-y-4=0 B.x+y-4=0
C.x=1 D.y=3
[答案] B
[解析] 当l1与l2之间距离最大时,l1⊥AB,故l1的斜率为-1.
6.(2015·重庆高考)已知直线l:x ( http: / / www.21cnjy.com )+ay-1=0(a∈R)是圆C:x2+y2-4x-2y+1=0的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|=( )
A.2 B.4
C.6 D.2
[答案] C
[解析] 易知圆的标准方程C:(x-2)2 ( http: / / www.21cnjy.com )+(y-1)2=4,圆心O为(2,1),又因为直线l:x+ay-1=0是圆的对称轴,则该直线一定经过圆心,得知a=-1,A(-4,-1)又因为AB直线与圆相切,则△OAB为直角三角形,|OA|==2,|OB|=2,
|AB|==6.
7.一块石材表示的几何体的三视图如图所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于( )2·1·c·n·j·y
A.1 B.2
C.3 D.4
[答案] B
[解析] 本题考查三视图及球的基础知识.
由图可得该几何体为三棱柱,所以最大球的半径为正视图直角三角形内切圆的半径r,则
r=- r=2,故选B.
直角三角形的内切圆半径为周长的一半减去斜边.
8. 三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=1,PB=PC=,则点P到平面ABC的距离是( )21·世纪*教育网
A. B.
C. D.1
[答案] A
[解析] 取BC中点D,∵PB⊥PC,PB=PC=,
∴PD=DC=BC=1,连AD,则AD⊥BC,且
AD==,∴S△ABC=×2×=.
由VP-ABC=VA-PBC,∴·S△ABC·h=·S△PBC·PA,
∴×h=××2,∴h=.
9.从原点O引圆(x-m)2+(y-2)2=m2+1的切线y=kx,当m变化时,切点P的轨迹方程是( )www-2-1-cnjy-com
A.x2+y2=3
B.(x-1)2+y2=2
C.(x-1)2+(y-1)2=3
D.x2+y2=2
[答案] A
[解析] 设切点P(x,y),圆心C(m, ( http: / / www.21cnjy.com )2),则在直角三角形OPC中,由勾股定理可得m2+4=m2+1+x2+y2,∴切点P的轨迹方程为x2+y2=3.2-1-c-n-j-y
10.如图所示,在酒泉卫星 ( http: / / www.21cnjy.com )发射场某试验区,用四根垂直于地面的立柱支撑着一个平行四边形的太阳能电池板,可测得其中三根立柱AA1、BB1、CC1的长度分别为10 m、15 m、30 m, 21*cnjy*com
则立柱DD1的长度是( )
A.30 m
B.25 m
C.20 m
D.15 m
[答案] B
[解析] 由题意知,CC1-DD1=BB1-AA1=5,
∴DD1=25 m.
11.已知正四棱锥P-ABCD的侧棱长为2a,侧面等腰三角形的顶角为30°,则从点A 出发环绕侧面一周后回到点A的最短距离为( )【来源:21·世纪·教育·网】
A.2a B.4a
C.6a D.12a
[答案] C
[解析] 将四棱锥的侧面展开,如图.所求最短距离为AA′,由AP=A′P=2a,
∠APA′=4×30°=120°,
∴AA′=AP·cos30°×2=2a××2=6a.
12.已知曲线C:x2+y2=2,点A(-2,0)及点B(2,a),如图,从点A观察点B,要使视线不被曲线C挡住,则a的取值范围是( )【来源:21cnj*y.co*m】
A.(-∞,-4)∪(4,+∞)
B.[-4,4]
C.(-∞,-1)∪(1,+∞)
D.(-∞,-2)∪(2,+∞)
[答案] A
[解析] 由题图可以得到切线AB的斜率为±1,∴>1或<-1,解得a<-4或a>4,故选A.
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在题中横线上)
13.已知直线ax+by+c=0与圆:x2+y2=1相交于A、B两点,且|AB|=,则∠AOB=________.【出处:21教育名师】
[答案] 120°
[解析] 如图所示,作OD⊥AB,
Rt△AOD中,OA=1,AD=,∴∠AOD=60°,
∴∠AOB=120°.
14.两圆(x+1)2+(y-1)2= ( http: / / www.21cnjy.com )r2和(x-2)2+(y+2)2=R2相交于P,Q两点,若点P的坐标为(1,2),则点Q的坐标为________.21世纪教育网版权所有
[答案] (-2,-1)
[解析] 两圆的圆心分别为O1(-1,1),O2(2,-2),直线O1O2的方程为y=-x.
由于两圆的交点为P,Q所以P,Q两点关于直线y=-x对称.
又点P的坐标为(1,2),则点Q的坐标为(-2,-1).
15.若正三棱台的上、下底面的边长为2和8,侧棱长为5,则这个棱台的高是________.
[答案]
[解析] 如图,设O1,O分别为上,下底面的中心,
则A1O1=××2=,AO=.
连接O1O,则O1O为高.
所以O1O=
==.
16.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是________.21教育名师原创作品
(1)PB⊥AD;
(2)平面PAB⊥平面PBC;
(3)直线BC∥平面PAE;
(4)∠PDA=45°.
[答案] (4)
[解析] 若PB⊥AD,则AD⊥AB,但AD与AB成60°角,(1)错误;
过A作AG⊥PB,若平面PAB⊥平面PBC,
∴AG⊥BC,
又∵PA⊥BC,
∴BC⊥平面PAB,∴BC⊥AB,矛盾,(2)错误;
BC与AE是相交直线,
∴直线BC一定不与平面PAE平行,(3)错误;
在Rt△PAD中,由于AD=2AB=PA,
∴∠PDA=45° ,(4)正确.
三、解答题(本大题共6个小题,满分70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)已知点A(2,-1),B(5,3),若直线l:kx-y+1=0与线段AB相交,求k的取值范围.
[解析] 解法1:由方程kx-y+1=0可知,
直线l恒过定点P(0,1),如图所示,
连接PA,PB,解得kPA=-1,kPB=.
又∵直线l的斜率为k,
∴k的取值范围为-1≤k≤.
解法2:由两点式求得直线AB的方程为4x-3y-11=0,
联立方程组
解得x=-,满足2≤≤5,
解得-1≤k≤.
18.(本小题满分12分)如图,在 ( http: / / www.21cnjy.com )△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°.www.21-cn-jy.com
(1)证明:平面ADB⊥平面BDC;
(2)若BD=1,求三棱锥D-ABC的表面积.
[解析] (1)∵折起前AD是BC边上的高.
∴当△ABD折起后,AD⊥DC,AD⊥DB,
又DB∩DC=D,
∴AD⊥平面BDC,
∵AD?平面ABD,
∴平面ABD⊥平面BDC.
(2)由(1)知,DA⊥DB,DB⊥DC,DC⊥DA,
∵DB=DA=DC=1,
∴AB=BC=CA=,
从而S△DAB=S△DBC=S△DCA=×1×1=,
S△ABC=×××sin60°=,
∴表面积S=×3+=.
19.(本小题满分12分)(2015·山东高考)如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.【版权所有:21教育】
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
[解析] (1)证法1:连接DG, ( http: / / www.21cnjy.com )CD.设CD∩GF=M,连接MH.在三棱台DEF-ABC中,AB=2DE,G为AC的中点,可得DF∥GC,DF=GC,21*cnjy*com
所以四边形DFCG是平行四边形,
则M为CD的中点,又H是BC的中点,所以HM∥BD,
又HM?平面FGH,BD平面FGH,所以BD∥平面FGH.
证法2:在三棱台DEF-ABC中,
由BC=2EF,H为BC的中点,可得BH∥EF,BH=EF,
所以四边形HBEF为平行四边形,可得BE∥HF.
在△ABC中,G,H分别为AC,BC的中点,
所以GH∥AB,
又GH∩HF=H,
所以平面FGH∥平面ABED,
因为BD?平面ABED,
所以BD∥平面FGH.
(2)连接HE.
因为G,H分别为AC,BC的中点,
所以GH∥AB.
由AB⊥BC,得GH⊥BC,
又H为BC的中点,
所以EF∥HC,EF=HC,
因此四边形EFCH是平行四边形,
所以CF∥HE.
又CF⊥BC,所以HE⊥BC.
又HE,GH?平面EGH,HE∩GH=H,
所以BC⊥平面EGH,
又BC?平面BCD,
所以平面BCD⊥平面EGH.
20.(本小题满分12分)求圆心在2+y2=2上,且与x轴,直线x=-都相切的圆的方程.
[解析] 设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),
则
即
解得a=,b=±1,r=1,
故所求圆的方程为:
2+(y-1)2=1或2+(y+1)2=1.
21.(本小题满分12分)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.
(1)若AC⊥BC,证明:直线BC⊥平面ACC1A1;
(2)设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.21·cn·jy·com
[解析] (1)因为四边形ABB1A1和ACC1A1都是矩形,
所以AA1⊥AB,AA1⊥AC.
因为AB,AC为平面ABC内两条相交直线,
所以AA1⊥平面ABC.
因为直线BC?平面ABC,所以AA1⊥BC.
又由已知,AC⊥BC,AA1,AC为平面ACC1A1内两条相交直线,
所以BC⊥平面ACC1A1.
(2)取线段AB的中点M,连接A1M,MC,A1C,AC1,设O为A1C,AC1的交点.
由已知,O为AC1的中点.
连接MD,OE,则MD,OE分别为△ABC,△ACC1的中位线,
所以,MDAC,OEAC,
因此MDOE.
连接OM,从而四边形MDEO为平行四边形,
则DE∥MO.
因为直线DE平面A1MC,MO?平面A1MC.
所以直线DE∥平面A1MC.
即线段AB上存在一点M(线段AB的中点),使直线DE∥平面A1MC.
22.(本小题满分12分)已知圆C的圆心在直线2x-y-3=0上,且经过点A(5,2),B(3,2),
(1)求圆C的标准方程;
(2)直线l过点P(2,1)且与圆C相交,所得弦长为2,求直线l的方程;
(3)设Q为圆C上一动点,O为坐标原点,试求△OPQ面积的最大值.
[解析] (1)设圆心P(x0,y0),由题意可知,圆心应在线段AB的中垂线上,其方程为x=4.
由得圆心P(4,5),
∴半径r=|PA|=.
∴圆的标准方程为(x-4)2+(y-5)2=10.
(2)当直线的斜率不存在时,直线方程为x=2,此时,圆心到直线的距离为2,符合题意.
当直线的斜率存在时,设直线方程为y-1=k(x-2),整理得kx-y+1-2k=0,
则圆心到直线的距离为d==.
由题意可知,d2+()2=r2,即+6=10,
解得k=.
故所求直线方程为3x-4y-2=0或x=2.
(3)直线OP的方程为y=x,即x-2y=0.
∴圆心到直线的距离为d==.
则圆上的点到直线的最大距离为d+r=+,
又∵|OP|==,
∴△OPQ面积的最大值为|OP|(d+r)=×=3+.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
本册综合测试二
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)21教育网
1.若空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2∥l3,l3⊥l4,则下列结论一定正确的是( )21cnjy.com
A.l1⊥l4
B.l1∥l4
C.l1与l4既不垂直也不平行
D.l1与l4的位置关系不确定
[答案] D
[解析] 本题考查空间中的平行关系.
通过作图可知l1与l4的位置关系不确定,选D,动手作试验是解决本题的好方法.
2. 直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,则m的值为( )
A.2 B.-3
C.2或-3 D.-2或-3
[答案] C
[解析] 解法1:l1:2x+(m+1)y+4=0,
l2:mx+3y-2=0,
当m=0时,显然l1不平行于l2;
当m≠0时,若l1∥l2,需=≠.①
由①式有m2+m-6=0,解得m=2,或m=-3.
显然m=2,或m=-3满足①.∴应选C.
解法2:若l1∥l2,需2×3-m(m+1)=0,解得m=-3,或m=2.
当m=-3或2时,A1C2-A2C1=2×(-2)-m·4=-4-4m≠0.
∴m=-3或2为所求.∴应选C.
3. 若a,b是异面直线,b,c是异面直线,则a,c的位置关系为( )
A.相交、平行或异面 B.相交或平行
C.异面 D.平行或异面
[答案] A
[解析] a与c可以相交、平行或异面,分别如下图中的(1),(2),(3).
4.已知某几何体的三视图如图所示,则该几何体的体积为( )
A. B.3π
C. D.6π
[答案] B
[解析] 本题考查几何体的三视图和体积计算.
由三视图还原几何体为补形后为圆柱,∴2V=π·6,
∴V=3π.补形法求几何体的体积非常简便.
5.分别过点A(1,3)和点B(2,4)的直线l1和l2互相平行且有最大距离,则l1的方程是( )
A.x-y-4=0 B.x+y-4=0
C.x=1 D.y=3
[答案] B
[解析] 当l1与l2之间距离最大时,l1⊥AB,故l1的斜率为-1.
6.(2015·重庆高考)已知直线l:x ( http: / / www.21cnjy.com )+ay-1=0(a∈R)是圆C:x2+y2-4x-2y+1=0的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|=( )
A.2 B.4
C.6 D.2
[答案] C
[解析] 易知圆的标准方程C:(x-2)2 ( http: / / www.21cnjy.com )+(y-1)2=4,圆心O为(2,1),又因为直线l:x+ay-1=0是圆的对称轴,则该直线一定经过圆心,得知a=-1,A(-4,-1)又因为AB直线与圆相切,则△OAB为直角三角形,|OA|==2,|OB|=2,
|AB|==6.
7.一块石材表示的几何体的三视图如图所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于( )2·1·c·n·j·y
A.1 B.2
C.3 D.4
[答案] B
[解析] 本题考查三视图及球的基础知识.
由图可得该几何体为三棱柱,所以最大球的半径为正视图直角三角形内切圆的半径r,则
r=- r=2,故选B.
直角三角形的内切圆半径为周长的一半减去斜边.
8. 三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=1,PB=PC=,则点P到平面ABC的距离是( )21·世纪*教育网
A. B.
C. D.1
[答案] A
[解析] 取BC中点D,∵PB⊥PC,PB=PC=,
∴PD=DC=BC=1,连AD,则AD⊥BC,且
AD==,∴S△ABC=×2×=.
由VP-ABC=VA-PBC,∴·S△ABC·h=·S△PBC·PA,
∴×h=××2,∴h=.
9.从原点O引圆(x-m)2+(y-2)2=m2+1的切线y=kx,当m变化时,切点P的轨迹方程是( )www-2-1-cnjy-com
A.x2+y2=3
B.(x-1)2+y2=2
C.(x-1)2+(y-1)2=3
D.x2+y2=2
[答案] A
[解析] 设切点P(x,y),圆心C(m, ( http: / / www.21cnjy.com )2),则在直角三角形OPC中,由勾股定理可得m2+4=m2+1+x2+y2,∴切点P的轨迹方程为x2+y2=3.2-1-c-n-j-y
10.如图所示,在酒泉卫星 ( http: / / www.21cnjy.com )发射场某试验区,用四根垂直于地面的立柱支撑着一个平行四边形的太阳能电池板,可测得其中三根立柱AA1、BB1、CC1的长度分别为10 m、15 m、30 m, 21*cnjy*com
则立柱DD1的长度是( )
A.30 m
B.25 m
C.20 m
D.15 m
[答案] B
[解析] 由题意知,CC1-DD1=BB1-AA1=5,
∴DD1=25 m.
11.已知正四棱锥P-ABCD的侧棱长为2a,侧面等腰三角形的顶角为30°,则从点A 出发环绕侧面一周后回到点A的最短距离为( )【来源:21·世纪·教育·网】
A.2a B.4a
C.6a D.12a
[答案] C
[解析] 将四棱锥的侧面展开,如图.所求最短距离为AA′,由AP=A′P=2a,
∠APA′=4×30°=120°,
∴AA′=AP·cos30°×2=2a××2=6a.
12.已知曲线C:x2+y2=2,点A(-2,0)及点B(2,a),如图,从点A观察点B,要使视线不被曲线C挡住,则a的取值范围是( )【来源:21cnj*y.co*m】
A.(-∞,-4)∪(4,+∞)
B.[-4,4]
C.(-∞,-1)∪(1,+∞)
D.(-∞,-2)∪(2,+∞)
[答案] A
[解析] 由题图可以得到切线AB的斜率为±1,∴>1或<-1,解得a<-4或a>4,故选A.
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在题中横线上)
13.已知直线ax+by+c=0与圆:x2+y2=1相交于A、B两点,且|AB|=,则∠AOB=________.【出处:21教育名师】
[答案] 120°
[解析] 如图所示,作OD⊥AB,
Rt△AOD中,OA=1,AD=,∴∠AOD=60°,
∴∠AOB=120°.
14.两圆(x+1)2+(y-1)2= ( http: / / www.21cnjy.com )r2和(x-2)2+(y+2)2=R2相交于P,Q两点,若点P的坐标为(1,2),则点Q的坐标为________.21世纪教育网版权所有
[答案] (-2,-1)
[解析] 两圆的圆心分别为O1(-1,1),O2(2,-2),直线O1O2的方程为y=-x.
由于两圆的交点为P,Q所以P,Q两点关于直线y=-x对称.
又点P的坐标为(1,2),则点Q的坐标为(-2,-1).
15.若正三棱台的上、下底面的边长为2和8,侧棱长为5,则这个棱台的高是________.
[答案]
[解析] 如图,设O1,O分别为上,下底面的中心,
则A1O1=××2=,AO=.
连接O1O,则O1O为高.
所以O1O=
==.
16.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是________.21教育名师原创作品
(1)PB⊥AD;
(2)平面PAB⊥平面PBC;
(3)直线BC∥平面PAE;
(4)∠PDA=45°.
[答案] (4)
[解析] 若PB⊥AD,则AD⊥AB,但AD与AB成60°角,(1)错误;
过A作AG⊥PB,若平面PAB⊥平面PBC,
∴AG⊥BC,
又∵PA⊥BC,
∴BC⊥平面PAB,∴BC⊥AB,矛盾,(2)错误;
BC与AE是相交直线,
∴直线BC一定不与平面PAE平行,(3)错误;
在Rt△PAD中,由于AD=2AB=PA,
∴∠PDA=45° ,(4)正确.
三、解答题(本大题共6个小题,满分70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)已知点A(2,-1),B(5,3),若直线l:kx-y+1=0与线段AB相交,求k的取值范围.
[解析] 解法1:由方程kx-y+1=0可知,
直线l恒过定点P(0,1),如图所示,
连接PA,PB,解得kPA=-1,kPB=.
又∵直线l的斜率为k,
∴k的取值范围为-1≤k≤.
解法2:由两点式求得直线AB的方程为4x-3y-11=0,
联立方程组
解得x=-,满足2≤≤5,
解得-1≤k≤.
18.(本小题满分12分)如图,在 ( http: / / www.21cnjy.com )△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°.www.21-cn-jy.com
(1)证明:平面ADB⊥平面BDC;
(2)若BD=1,求三棱锥D-ABC的表面积.
[解析] (1)∵折起前AD是BC边上的高.
∴当△ABD折起后,AD⊥DC,AD⊥DB,
又DB∩DC=D,
∴AD⊥平面BDC,
∵AD?平面ABD,
∴平面ABD⊥平面BDC.
(2)由(1)知,DA⊥DB,DB⊥DC,DC⊥DA,
∵DB=DA=DC=1,
∴AB=BC=CA=,
从而S△DAB=S△DBC=S△DCA=×1×1=,
S△ABC=×××sin60°=,
∴表面积S=×3+=.
19.(本小题满分12分)(2015·山东高考)如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.【版权所有:21教育】
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
[解析] (1)证法1:连接DG, ( http: / / www.21cnjy.com )CD.设CD∩GF=M,连接MH.在三棱台DEF-ABC中,AB=2DE,G为AC的中点,可得DF∥GC,DF=GC,21*cnjy*com
所以四边形DFCG是平行四边形,
则M为CD的中点,又H是BC的中点,所以HM∥BD,
又HM?平面FGH,BD平面FGH,所以BD∥平面FGH.
证法2:在三棱台DEF-ABC中,
由BC=2EF,H为BC的中点,可得BH∥EF,BH=EF,
所以四边形HBEF为平行四边形,可得BE∥HF.
在△ABC中,G,H分别为AC,BC的中点,
所以GH∥AB,
又GH∩HF=H,
所以平面FGH∥平面ABED,
因为BD?平面ABED,
所以BD∥平面FGH.
(2)连接HE.
因为G,H分别为AC,BC的中点,
所以GH∥AB.
由AB⊥BC,得GH⊥BC,
又H为BC的中点,
所以EF∥HC,EF=HC,
因此四边形EFCH是平行四边形,
所以CF∥HE.
又CF⊥BC,所以HE⊥BC.
又HE,GH?平面EGH,HE∩GH=H,
所以BC⊥平面EGH,
又BC?平面BCD,
所以平面BCD⊥平面EGH.
20.(本小题满分12分)求圆心在2+y2=2上,且与x轴,直线x=-都相切的圆的方程.
[解析] 设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),
则
即
解得a=,b=±1,r=1,
故所求圆的方程为:
2+(y-1)2=1或2+(y+1)2=1.
21.(本小题满分12分)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.
(1)若AC⊥BC,证明:直线BC⊥平面ACC1A1;
(2)设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.21·cn·jy·com
[解析] (1)因为四边形ABB1A1和ACC1A1都是矩形,
所以AA1⊥AB,AA1⊥AC.
因为AB,AC为平面ABC内两条相交直线,
所以AA1⊥平面ABC.
因为直线BC?平面ABC,所以AA1⊥BC.
又由已知,AC⊥BC,AA1,AC为平面ACC1A1内两条相交直线,
所以BC⊥平面ACC1A1.
(2)取线段AB的中点M,连接A1M,MC,A1C,AC1,设O为A1C,AC1的交点.
由已知,O为AC1的中点.
连接MD,OE,则MD,OE分别为△ABC,△ACC1的中位线,
所以,MDAC,OEAC,
因此MDOE.
连接OM,从而四边形MDEO为平行四边形,
则DE∥MO.
因为直线DE平面A1MC,MO?平面A1MC.
所以直线DE∥平面A1MC.
即线段AB上存在一点M(线段AB的中点),使直线DE∥平面A1MC.
22.(本小题满分12分)已知圆C的圆心在直线2x-y-3=0上,且经过点A(5,2),B(3,2),
(1)求圆C的标准方程;
(2)直线l过点P(2,1)且与圆C相交,所得弦长为2,求直线l的方程;
(3)设Q为圆C上一动点,O为坐标原点,试求△OPQ面积的最大值.
[解析] (1)设圆心P(x0,y0),由题意可知,圆心应在线段AB的中垂线上,其方程为x=4.
由得圆心P(4,5),
∴半径r=|PA|=.
∴圆的标准方程为(x-4)2+(y-5)2=10.
(2)当直线的斜率不存在时,直线方程为x=2,此时,圆心到直线的距离为2,符合题意.
当直线的斜率存在时,设直线方程为y-1=k(x-2),整理得kx-y+1-2k=0,
则圆心到直线的距离为d==.
由题意可知,d2+()2=r2,即+6=10,
解得k=.
故所求直线方程为3x-4y-2=0或x=2.
(3)直线OP的方程为y=x,即x-2y=0.
∴圆心到直线的距离为d==.
则圆上的点到直线的最大距离为d+r=+,
又∵|OP|==,
∴△OPQ面积的最大值为|OP|(d+r)=×=3+.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
