25.3 相似三角形 分层作业(含答案) 2023-2024学年初中数学冀教版九年级上册
文档属性
| 名称 | 25.3 相似三角形 分层作业(含答案) 2023-2024学年初中数学冀教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 120.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 15:07:02 | ||
图片预览


文档简介
25.3 相似三角形
【练基础】
必备知识1 相似三角形的有关概念
1.如图,△ADE∽△ABC,且AD∶DB=1∶3,则△ADE与△ABC的相似比为 ( )
A.1∶3 B.1∶4 C.3∶1 D.4∶1
2.如图,△ABC∽△DAC,∠B=36°,∠D=117°,则∠BAD的度数为 ( )
A.36° B.117° C.143° D.153°
3.如图,已知△ACD∽△ADB,AC=4,AD=2,则AB的长为 ( )
A.1
B.2
C.3
D.4
4.已知△ABC三边的长分别是2 cm,3 cm,4 cm,与其相似的△DEF的最短边是8 cm,那么它的最长边的边长是 cm.
必备知识2 利用平行线分线段成比例判定两个三角形相似
5.如图,DE∥FG∥BC,则图中相似三角形的对数为 ( )
A.3 B.2 C.1 D.0
6.如图,E是平行四边形ABCD的边BC的延长线上的一点,连接AE交CD于点F,则图中相似三角形共有 ( )
A.1对 B.2对 C.3对 D.4对
7.如图,在△ABC中,点D在BC上,EF∥BC,且分别交AB,AC,AD于点E,F,G,图中共有几对相似三角形 分别是哪几对
8.如图,AB与CD相交于点E,AE=EB,CE=ED,D为线段FB的中点,CF与AB交于点G,若CF=15 cm,求GF的长.
【练能力】
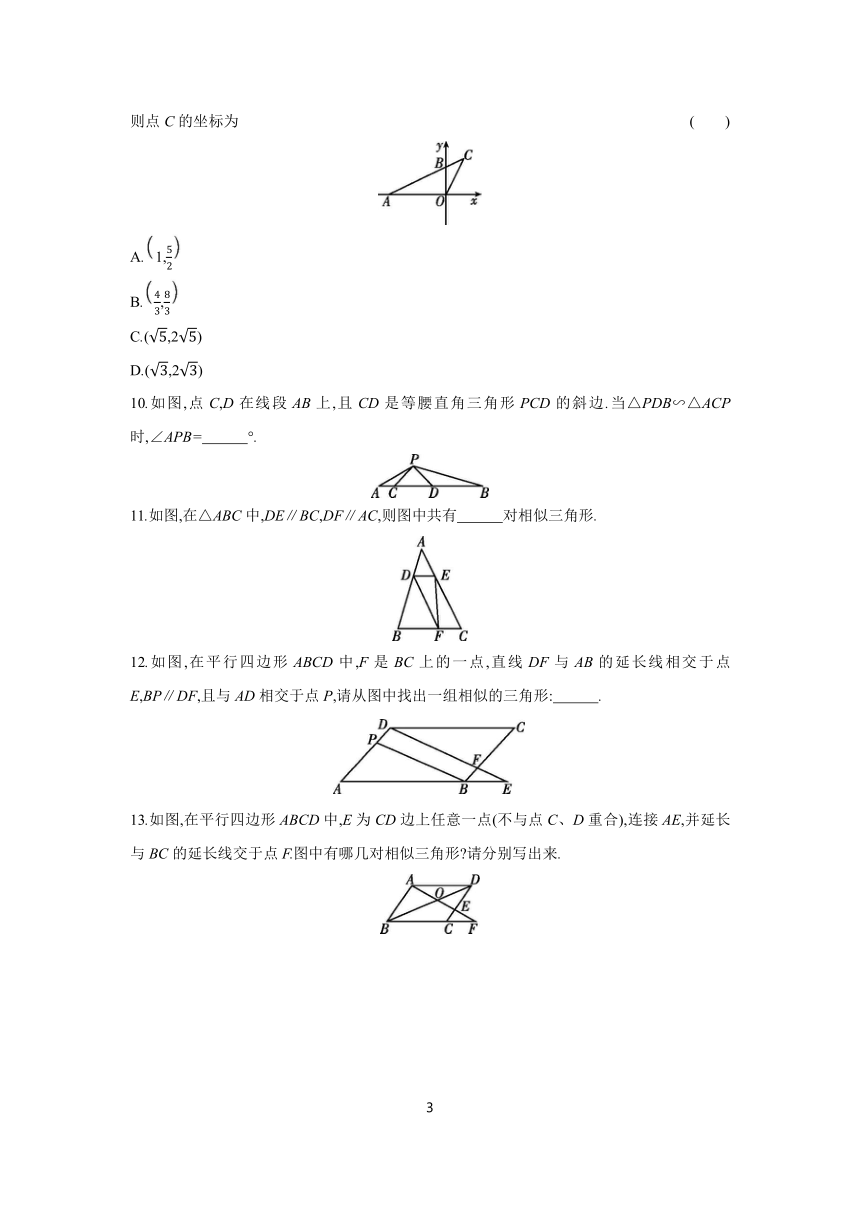
9.如图,在直角坐标系xOy中,A(-4,0),B(0,2),连接AB并延长到点C,连接CO,若△COB∽△CAO,则点C的坐标为 ( )
A.1,
B.,
C.(,2)
D.(,2)
10.如图,点C,D在线段AB上,且CD是等腰直角三角形PCD的斜边.当△PDB∽△ACP时,∠APB= °.
11.如图,在△ABC中,DE∥BC,DF∥AC,则图中共有 对相似三角形.
12.如图,在平行四边形ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出一组相似的三角形: .
13.如图,在平行四边形ABCD中,E为CD边上任意一点(不与点C、D重合),连接AE,并延长与BC的延长线交于点F.图中有哪几对相似三角形 请分别写出来.
14.如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,△ADE和△EFC相似吗 为什么
【练素养】
15.从三角形(不是等腰三角形)一个顶点引一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,已知∠A=48°,CD是△ABC的完美分割线,且AD=CD,则∠ACB= .
(2)如图2,在△ABC中,AC=2,BC=,若CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
参考答案
练基础
1.B 2.D 3.A 4.16 5.A 6.C
7.【解析】共有3对相似三角形,分别是△AEG∽△ABD,△AGF∽△ADC,△AEF∽△ABC.
8.【解析】∵AE=BE,∠AEC=∠BED,CE=DE,∴△AEC≌△BED,
∴∠CAE=∠B,∴AC∥FB,
∴△AGC∽△BGF,∴=.
∵△AEC≌△BED,D为线段FB的中点,
∴AC=BD=FB,∴=,∴==,
又∵CF=15 cm,∴GF=10 cm.
练能力
9.B 10.135 11.4 12.△ABP∽△AED(或△BEF∽△CDF或△EBF∽△EAD等)
13.【解析】图中相似三角形有6对:
△AOD∽△FOB,△ADE∽△FCE,
△AOB∽△EOD,△ABD∽△CDB,
△FCE∽△FBA,△ADE∽△FBA.
14.【解析】△ADE∽△EFC.
∵DE∥BC,
∴△ADE∽△ABC.
∵EF∥AB,
∴△EFC∽△ABC,
∴△ADE∽△EFC.
练素养
15.【解析】(1)当AD=CD时,∠ACD=∠A=48°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∴∠ACB=∠ACD+∠BCD=96°.
(2)∵△BCD∽△BAC,∴=,设BD=x.
∵AC=AD=2,∴()2=x(x+2),
∵x>0,∴x=-1.∵△BCD∽△BAC,
∴=,=,
∴CD=×2=-.
2
【练基础】
必备知识1 相似三角形的有关概念
1.如图,△ADE∽△ABC,且AD∶DB=1∶3,则△ADE与△ABC的相似比为 ( )
A.1∶3 B.1∶4 C.3∶1 D.4∶1
2.如图,△ABC∽△DAC,∠B=36°,∠D=117°,则∠BAD的度数为 ( )
A.36° B.117° C.143° D.153°
3.如图,已知△ACD∽△ADB,AC=4,AD=2,则AB的长为 ( )
A.1
B.2
C.3
D.4
4.已知△ABC三边的长分别是2 cm,3 cm,4 cm,与其相似的△DEF的最短边是8 cm,那么它的最长边的边长是 cm.
必备知识2 利用平行线分线段成比例判定两个三角形相似
5.如图,DE∥FG∥BC,则图中相似三角形的对数为 ( )
A.3 B.2 C.1 D.0
6.如图,E是平行四边形ABCD的边BC的延长线上的一点,连接AE交CD于点F,则图中相似三角形共有 ( )
A.1对 B.2对 C.3对 D.4对
7.如图,在△ABC中,点D在BC上,EF∥BC,且分别交AB,AC,AD于点E,F,G,图中共有几对相似三角形 分别是哪几对
8.如图,AB与CD相交于点E,AE=EB,CE=ED,D为线段FB的中点,CF与AB交于点G,若CF=15 cm,求GF的长.
【练能力】
9.如图,在直角坐标系xOy中,A(-4,0),B(0,2),连接AB并延长到点C,连接CO,若△COB∽△CAO,则点C的坐标为 ( )
A.1,
B.,
C.(,2)
D.(,2)
10.如图,点C,D在线段AB上,且CD是等腰直角三角形PCD的斜边.当△PDB∽△ACP时,∠APB= °.
11.如图,在△ABC中,DE∥BC,DF∥AC,则图中共有 对相似三角形.
12.如图,在平行四边形ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出一组相似的三角形: .
13.如图,在平行四边形ABCD中,E为CD边上任意一点(不与点C、D重合),连接AE,并延长与BC的延长线交于点F.图中有哪几对相似三角形 请分别写出来.
14.如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,△ADE和△EFC相似吗 为什么
【练素养】
15.从三角形(不是等腰三角形)一个顶点引一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,已知∠A=48°,CD是△ABC的完美分割线,且AD=CD,则∠ACB= .
(2)如图2,在△ABC中,AC=2,BC=,若CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
参考答案
练基础
1.B 2.D 3.A 4.16 5.A 6.C
7.【解析】共有3对相似三角形,分别是△AEG∽△ABD,△AGF∽△ADC,△AEF∽△ABC.
8.【解析】∵AE=BE,∠AEC=∠BED,CE=DE,∴△AEC≌△BED,
∴∠CAE=∠B,∴AC∥FB,
∴△AGC∽△BGF,∴=.
∵△AEC≌△BED,D为线段FB的中点,
∴AC=BD=FB,∴=,∴==,
又∵CF=15 cm,∴GF=10 cm.
练能力
9.B 10.135 11.4 12.△ABP∽△AED(或△BEF∽△CDF或△EBF∽△EAD等)
13.【解析】图中相似三角形有6对:
△AOD∽△FOB,△ADE∽△FCE,
△AOB∽△EOD,△ABD∽△CDB,
△FCE∽△FBA,△ADE∽△FBA.
14.【解析】△ADE∽△EFC.
∵DE∥BC,
∴△ADE∽△ABC.
∵EF∥AB,
∴△EFC∽△ABC,
∴△ADE∽△EFC.
练素养
15.【解析】(1)当AD=CD时,∠ACD=∠A=48°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∴∠ACB=∠ACD+∠BCD=96°.
(2)∵△BCD∽△BAC,∴=,设BD=x.
∵AC=AD=2,∴()2=x(x+2),
∵x>0,∴x=-1.∵△BCD∽△BAC,
∴=,=,
∴CD=×2=-.
2
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
