最新人教版七下数学 8.2 加减法 ( 第2课时)26张PPT
文档属性
| 名称 | 最新人教版七下数学 8.2 加减法 ( 第2课时)26张PPT |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 16:52:09 | ||
图片预览








文档简介
(共26张PPT)
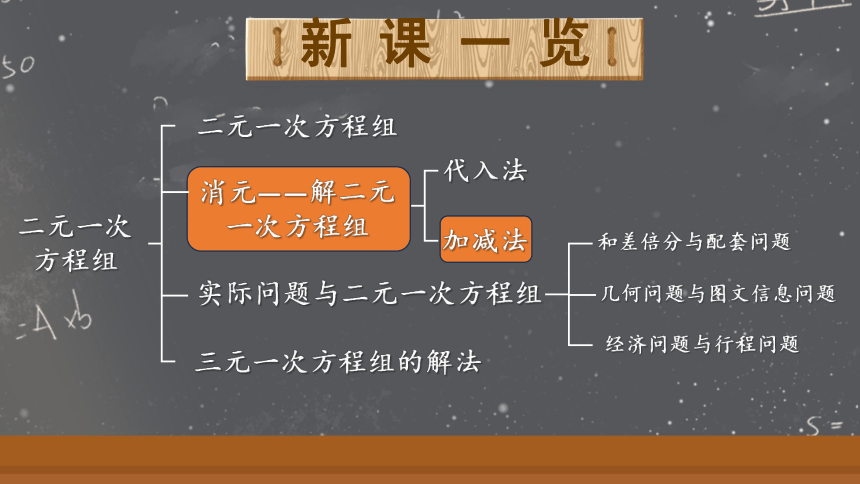
二元一次方程组
消元——解二元一次方程组
实际问题与二元一次方程组
三元一次方程组的解法
二元一次方程组
代入法
加减法
和差倍分与配套问题
几何问题与图文信息问题
经济问题与行程问题
新课一览
消元——解二元一次方程组
第2课时 加减法
人教版·七年级下册
二元一次方程组
8
回顾导入
在前面的课时,我们研究完了用代入法解一元二次方程组,这种方法的基本思想是_______,即把二元一次方程组转化为一元一次方程.
除了用代入法消元外,还有没有其他的方法消元呢?大家看下面3个问题:
①如果a=b,那么a±c=______.
②如果a=b,那么ac=_______.
③如果a=b,c=d,那么a±c=b±d成立吗?为什么?
消元
b±c
bc
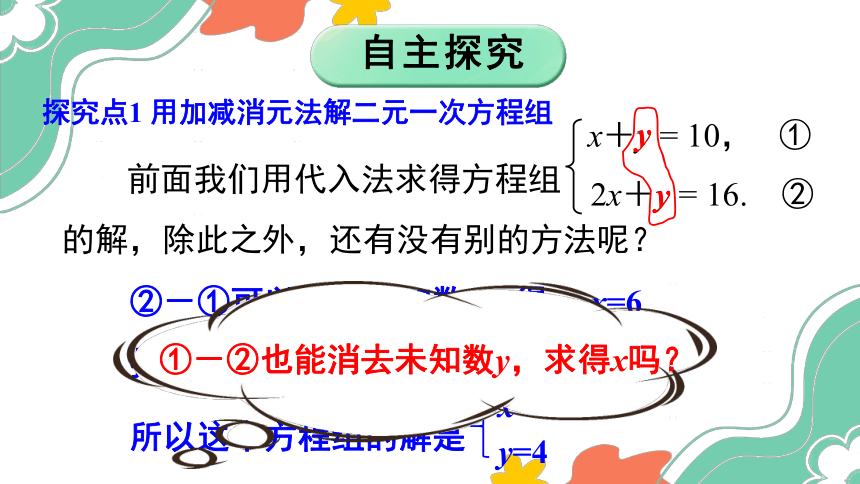
x+y = 10, ①
2x+y = 16. ②
前面我们用代入法求得方程组 的解,除此之外,还有没有别的方法呢?
y
y
②-①可以消去未知数y,得 x=6
把x=6代入①,得 y=4
所以这个方程组的解是
x=6
y=4
①-②也能消去未知数y,求得x吗?
自主探究
探究点1 用加减消元法解二元一次方程组
3x + 10y = 2.8, ①
15x - 10y = 8 . ②
解:将 ① + ② 得 18x=10.8,
x=0.6.
把 x=0.6 代入 ①,得
3×0.6 + 10y=2.8.
解得 y=0.1.
解方程组:
所以这个方程组的解是
x = 0.6,
y = 0.1.
+ 10y
10y
-
当二元一次方程组的两个方程中同一未知数的系数____或____时,把这两个方程的两边分别__________就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法..
相反
相等
相加或相减
例3 用加减法解方程组
3x+4y =16, ①
5x-6y =33. ②
直接加减不能消元,要怎样解这个方程组呢?
自主探究
解:①×3,得9x+12y=48. ③
②×2,得10x-12y=66. ④
………………变形
③+④,得19x=114,
………………加减
3x+4y =16, ①
5x-6y =33. ②
x=6.
………………求解
把x=6代入①,得3×6+4y=16,4y=-2,y=-0.5.
………………回代
……………写解
所以这个方程组的解是
x=6,
y=-0.5.
把x=6代入②可以解得y吗?
3x+4y =16, ①
5x-6y =33. ②
解:①×5,得9x+12y=48. ③
②×3,得10x-12y=66. ④
③-④,得39y=-19,
y=-0.5.
把y=-0.5代入①,得3x-2=16,x=6
所以这个方程组的解是
x=6,
y=-0.5.
如果用加减法消去x应如何解?
解方程组时,先消去哪个未知数都可以,结果是确定的,不会因为先消去哪个未知数而产生变化,一般地,先消去哪个未知数简便就先消去哪个.
x + 3y = 8, ①
5x + 3y = 16. ②
1. 请用加减法解二元一次方程组:
解:②-① 得 4x = 8.
x = 2
解得 y = 2.
所以原方程组的解为
x = 2,
y = 2.
将 x = 2 代入①得 2 + 3y = 8
对应练习
2. 用加减法解方程组:
①
②
①×3 得
所以原方程组的解是
解:
③ - ④ 得 y = 2.
把 y=2 代入 ①,
解得 x=3.
②×2 得
6x + 9y = 36. ③
6x + 8y = 34. ④
加减法求二元一次方程技巧:同一未知数
两式相加/减
找最小公倍数,系数变相同或相反
否
是
系数
相等或相反
例2 2 台大收割机和 5 台小收割机同时工作 2 h 共收割小麦 3.6 hm2,3 台大收割机和 2 台小收割机同时工作 5 h 收割小麦 8 hm2. 1 台大收割机和 1 台小收割机每小时各收割小麦多少公顷?
等量关系:
(1) 2 台大收割机 2 小时的工作量
+ 5 台小收割机 2 小时的工作量=3.6;
(2) 3 台大收割机 5 小时的工作量
+ 2 台小收割机 5 小时的工作量=8.
探究点2 加减消元法解二元一次方程组的简单应用
解:设 1 台大收割机和 1 台小收割机每小时分别收割小麦 x hm2 和 y hm2 .
2(2x + 5y) = 3.6,
5(3x + 2y) = 8.
怎么解这个方程组呢?先试着自己解一解.
2(2x + 5y) = 3.6,
5(3x + 2y) = 8.
去括号,得
4x + 10y = 3.6,
15x + 10y = 8.
①
②
②-①,得11x=4.4.解这个方程,得x=0.4
把x=0.4代入①,得y=0.2.
因此,这个方程组的解是
y=0.2
x=0.4
答:1台大收割机和1台小收割机每小时各收割小麦0.4hm2和0.2hm2.
上面解方程组的过程可以用下面的框图表示:
4x + 10y = 3.6 ①
15x + 10y = 8 ②
一元一次方程11x=4.4
y=0.2
x=0.4
解得y
解得x
②-①
两方程相减,消去未知数y
二元一次方程组
1.用加减法解下列方程组:
x+2y=9
3x-2y=-1
5x+2y=25
3x+4y=15
(1)
(2)
2x+5y=8
3x+2y=5
2x+3y=6
3x-2y=-2
(3)
(4)
课堂练习
【选自教材P96 练习第1题】
x+2y=9
3x-2y=-1
5x+2y=25
3x+4y=15
(1)
(2)
解:②+① 得 4x = 8.
x = 2
解得 y =
将 x = 2 代入①得 2 + 2y = 9
所以原方程组的解为
x = 2,
①
②
①
②
①×2 得
所以原方程组的解是
解:
③ - ② 得 7x=35 解得x = 5.
把 x=5 代入 ①,解得 y=0.
10x + 4y = 50. ③
2x+5y=8
3x+2y=5
2x+3y=6
3x-2y=-2
(3)
(4)
①
②
①×2 得
所以原方程组的解是
解:
④ - ③ 得 11x= 9. 解得
把 代入 ①, 解得 .
②×5 得
4x + 10y = 16. ③
15x + 10y = 25. ④
①
②
①×2 得
所以原方程组的解是
解:
③ + ④得 13x= 6. 解得
把 代入 ①, 解得 .
②×3 得
4x + 6y = 12. ③
9x - 6y = -6. ④
2.一条船顺流航行,每小时行20km;逆流航行,每小时行16km.求轮船在静水中的速度与水的流速.
解:设轮船在静水中的速度为x km/h,水的流速为y km/h.
根据题意,得,
解得,
答:轮船在静水中的速度为18km/h,
水的流速为2km/h.
x+y=20
x-y=16
x=18
y=2
【选自教材P97 练习第2题】
3.运输360 t化肥,装载了6节火车车厢和15辆汽车;
运输440 t化肥,装载了8节火车车厢和10辆汽车,每节火车车厢与每辆汽车平均各装多少吨化肥?
解:设每节火车车厢平均装 x 吨化肥,每辆汽车平均装 y 吨化肥.
依题意,得,
解得,
答:每节火车车厢平均装 50 吨化肥,每辆汽车平
均装 4 吨化肥.
6x+15y=360
8x+10y=440
x=50
y=4
【选自教材P97 练习第3题】
代入消元法和加减消元法是二元一次方程组的两种解法,它们都是通过消元使方程组转化为一元一次方程,只是消元的方法不同,我们应根据方程组的具体情况,选择适合它的解法.
(1)你怎样解下面的方程组?
2x+y=1.5
0.8x+0.6y=1.3
x+2y=3
3x-2y=5
思考
代入法
x=-1
y=3.5
解得,
加减法
x=2
y=0.5
解得,
2.我国古代数学著作《孙子算经》中有“鸡兔同笼”
问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”你能用二元一次方程组表示题中的数量关系吗?试找出问题的解.
解:设笼中有鸡x只,兔子y只.
依题意,得 解得
答:笼中有鸡23只,兔子12只.
x+y=35
2x+4y=94
x=23
y=12
实际问题
二元一次方程组
消元思想
代入消元法
加减消元法
课堂小结
课后作业
1.教材P97习题8.2第3,5,6,7,8,9题.
2.《创优作业》主体本部分相应课时训练.
二元一次方程组
消元——解二元一次方程组
实际问题与二元一次方程组
三元一次方程组的解法
二元一次方程组
代入法
加减法
和差倍分与配套问题
几何问题与图文信息问题
经济问题与行程问题
新课一览
消元——解二元一次方程组
第2课时 加减法
人教版·七年级下册
二元一次方程组
8
回顾导入
在前面的课时,我们研究完了用代入法解一元二次方程组,这种方法的基本思想是_______,即把二元一次方程组转化为一元一次方程.
除了用代入法消元外,还有没有其他的方法消元呢?大家看下面3个问题:
①如果a=b,那么a±c=______.
②如果a=b,那么ac=_______.
③如果a=b,c=d,那么a±c=b±d成立吗?为什么?
消元
b±c
bc
x+y = 10, ①
2x+y = 16. ②
前面我们用代入法求得方程组 的解,除此之外,还有没有别的方法呢?
y
y
②-①可以消去未知数y,得 x=6
把x=6代入①,得 y=4
所以这个方程组的解是
x=6
y=4
①-②也能消去未知数y,求得x吗?
自主探究
探究点1 用加减消元法解二元一次方程组
3x + 10y = 2.8, ①
15x - 10y = 8 . ②
解:将 ① + ② 得 18x=10.8,
x=0.6.
把 x=0.6 代入 ①,得
3×0.6 + 10y=2.8.
解得 y=0.1.
解方程组:
所以这个方程组的解是
x = 0.6,
y = 0.1.
+ 10y
10y
-
当二元一次方程组的两个方程中同一未知数的系数____或____时,把这两个方程的两边分别__________就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法..
相反
相等
相加或相减
例3 用加减法解方程组
3x+4y =16, ①
5x-6y =33. ②
直接加减不能消元,要怎样解这个方程组呢?
自主探究
解:①×3,得9x+12y=48. ③
②×2,得10x-12y=66. ④
………………变形
③+④,得19x=114,
………………加减
3x+4y =16, ①
5x-6y =33. ②
x=6.
………………求解
把x=6代入①,得3×6+4y=16,4y=-2,y=-0.5.
………………回代
……………写解
所以这个方程组的解是
x=6,
y=-0.5.
把x=6代入②可以解得y吗?
3x+4y =16, ①
5x-6y =33. ②
解:①×5,得9x+12y=48. ③
②×3,得10x-12y=66. ④
③-④,得39y=-19,
y=-0.5.
把y=-0.5代入①,得3x-2=16,x=6
所以这个方程组的解是
x=6,
y=-0.5.
如果用加减法消去x应如何解?
解方程组时,先消去哪个未知数都可以,结果是确定的,不会因为先消去哪个未知数而产生变化,一般地,先消去哪个未知数简便就先消去哪个.
x + 3y = 8, ①
5x + 3y = 16. ②
1. 请用加减法解二元一次方程组:
解:②-① 得 4x = 8.
x = 2
解得 y = 2.
所以原方程组的解为
x = 2,
y = 2.
将 x = 2 代入①得 2 + 3y = 8
对应练习
2. 用加减法解方程组:
①
②
①×3 得
所以原方程组的解是
解:
③ - ④ 得 y = 2.
把 y=2 代入 ①,
解得 x=3.
②×2 得
6x + 9y = 36. ③
6x + 8y = 34. ④
加减法求二元一次方程技巧:同一未知数
两式相加/减
找最小公倍数,系数变相同或相反
否
是
系数
相等或相反
例2 2 台大收割机和 5 台小收割机同时工作 2 h 共收割小麦 3.6 hm2,3 台大收割机和 2 台小收割机同时工作 5 h 收割小麦 8 hm2. 1 台大收割机和 1 台小收割机每小时各收割小麦多少公顷?
等量关系:
(1) 2 台大收割机 2 小时的工作量
+ 5 台小收割机 2 小时的工作量=3.6;
(2) 3 台大收割机 5 小时的工作量
+ 2 台小收割机 5 小时的工作量=8.
探究点2 加减消元法解二元一次方程组的简单应用
解:设 1 台大收割机和 1 台小收割机每小时分别收割小麦 x hm2 和 y hm2 .
2(2x + 5y) = 3.6,
5(3x + 2y) = 8.
怎么解这个方程组呢?先试着自己解一解.
2(2x + 5y) = 3.6,
5(3x + 2y) = 8.
去括号,得
4x + 10y = 3.6,
15x + 10y = 8.
①
②
②-①,得11x=4.4.解这个方程,得x=0.4
把x=0.4代入①,得y=0.2.
因此,这个方程组的解是
y=0.2
x=0.4
答:1台大收割机和1台小收割机每小时各收割小麦0.4hm2和0.2hm2.
上面解方程组的过程可以用下面的框图表示:
4x + 10y = 3.6 ①
15x + 10y = 8 ②
一元一次方程11x=4.4
y=0.2
x=0.4
解得y
解得x
②-①
两方程相减,消去未知数y
二元一次方程组
1.用加减法解下列方程组:
x+2y=9
3x-2y=-1
5x+2y=25
3x+4y=15
(1)
(2)
2x+5y=8
3x+2y=5
2x+3y=6
3x-2y=-2
(3)
(4)
课堂练习
【选自教材P96 练习第1题】
x+2y=9
3x-2y=-1
5x+2y=25
3x+4y=15
(1)
(2)
解:②+① 得 4x = 8.
x = 2
解得 y =
将 x = 2 代入①得 2 + 2y = 9
所以原方程组的解为
x = 2,
①
②
①
②
①×2 得
所以原方程组的解是
解:
③ - ② 得 7x=35 解得x = 5.
把 x=5 代入 ①,解得 y=0.
10x + 4y = 50. ③
2x+5y=8
3x+2y=5
2x+3y=6
3x-2y=-2
(3)
(4)
①
②
①×2 得
所以原方程组的解是
解:
④ - ③ 得 11x= 9. 解得
把 代入 ①, 解得 .
②×5 得
4x + 10y = 16. ③
15x + 10y = 25. ④
①
②
①×2 得
所以原方程组的解是
解:
③ + ④得 13x= 6. 解得
把 代入 ①, 解得 .
②×3 得
4x + 6y = 12. ③
9x - 6y = -6. ④
2.一条船顺流航行,每小时行20km;逆流航行,每小时行16km.求轮船在静水中的速度与水的流速.
解:设轮船在静水中的速度为x km/h,水的流速为y km/h.
根据题意,得,
解得,
答:轮船在静水中的速度为18km/h,
水的流速为2km/h.
x+y=20
x-y=16
x=18
y=2
【选自教材P97 练习第2题】
3.运输360 t化肥,装载了6节火车车厢和15辆汽车;
运输440 t化肥,装载了8节火车车厢和10辆汽车,每节火车车厢与每辆汽车平均各装多少吨化肥?
解:设每节火车车厢平均装 x 吨化肥,每辆汽车平均装 y 吨化肥.
依题意,得,
解得,
答:每节火车车厢平均装 50 吨化肥,每辆汽车平
均装 4 吨化肥.
6x+15y=360
8x+10y=440
x=50
y=4
【选自教材P97 练习第3题】
代入消元法和加减消元法是二元一次方程组的两种解法,它们都是通过消元使方程组转化为一元一次方程,只是消元的方法不同,我们应根据方程组的具体情况,选择适合它的解法.
(1)你怎样解下面的方程组?
2x+y=1.5
0.8x+0.6y=1.3
x+2y=3
3x-2y=5
思考
代入法
x=-1
y=3.5
解得,
加减法
x=2
y=0.5
解得,
2.我国古代数学著作《孙子算经》中有“鸡兔同笼”
问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”你能用二元一次方程组表示题中的数量关系吗?试找出问题的解.
解:设笼中有鸡x只,兔子y只.
依题意,得 解得
答:笼中有鸡23只,兔子12只.
x+y=35
2x+4y=94
x=23
y=12
实际问题
二元一次方程组
消元思想
代入消元法
加减消元法
课堂小结
课后作业
1.教材P97习题8.2第3,5,6,7,8,9题.
2.《创优作业》主体本部分相应课时训练.
