最新人教版七下数学 8.3 实际问题与二元一次方程组 第3课时 经济问题与行程问题 课件(共16张PPT)
文档属性
| 名称 | 最新人教版七下数学 8.3 实际问题与二元一次方程组 第3课时 经济问题与行程问题 课件(共16张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
二元一次方程组
消元——解二元一次方程组
实际问题与二元一次方程组
三元一次方程组的解法
二元一次方程组
代入法
加减法
和差倍分与配套问题
几何问题与图文信息问题
经济问题与行程问题
新课一览
二元一次方程组
实际问题与二元一次方程组
8
第3课时 经济问题与行程问题
人教版·七年级下册
回顾导入
填一填:
(1)某工厂去年的总产值是x万元,今年的总产值比去年增加了20%,则今年的总产值是______________万元;
(2)若该厂去年的总支出是y万元,今年的总支出比去年减少了10%,则今年的总支出是______________万元;
(3)若该厂今年的利润比去年增加了50%,则结合(1)(2)可列方程为_________________________________.
(1+20%)x
(1-10%)y
(1+20%)x-(1-10%)y=(1+50%)(x-y)
探究3
如图,长青化工厂与 A,B 两地有公路、铁路相连.这家工厂从 A 地购买一批每吨1000元的原料运回工厂,制成每吨 8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
产品的销售款-(原料款+运输费)=净利润
自主探究
产品 x t 原料 y t 合 计
公路运费(元)
铁路运费(元)
价值(元)
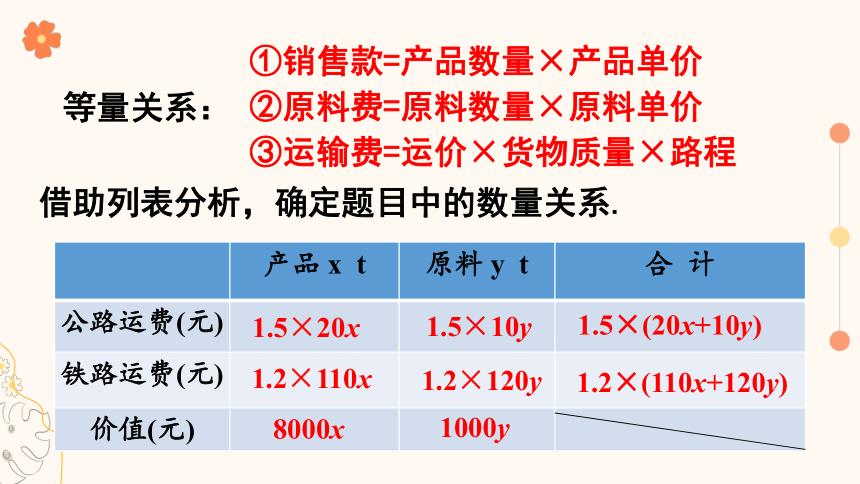
借助列表分析,确定题目中的数量关系.
1.5×20x
1.2×110x
8000x
1.5×10y
1.2×120y
1000y
1.5×(20x+10y)
1.2×(110x+120y)
等量关系:
①销售款=产品数量×产品单价
②原料费=原料数量×原料单价
③运输费=运价×货物质量×路程
根据上表中运费之间的关系,列出方程组,
因此,这批产品的销售款比原料费与运输费的和多_________元.
1887800
1.5×(20x+10y)=15000
1.2×(110x+120y)=97200
整理,得
2x+y=1000
11x+12y=8100
解这个方程组,得
x=300
y=400
8000×300-1000×400-15000-97200=1887800(元)
对于复杂的实际问题,可以通过列表的方法将所有的数量关系进行整理,发现等量关系,列出方程组.
如图,A,B两地由公路和铁路相连,在这条路上有一家食品厂,它到B地的路程是到A地路程的2倍.该食品厂从A地收购一批食材运回食品厂,全部加工成食品(制作过程中有损耗)运到B地销售,两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.已知公路运费为1.5元/(t. km),铁路运费为1元/(t. km).
(1)这家食品厂到A,B两地的路程分别是多少千米?
(2)若这家食品厂此次收购的食材每吨花费5000元,要想该批食品销售完后.工厂共获利863800元,则这批食品每吨的售价应为多少元?(利润=
总售价-总成本-总运费)
对应练习
解:(1)设这家食品厂到A地的路程是xkm,到B地的路程是ykm.
根据题意,得
x+y=20+100+30
y=2x
解这个方程组,得
x=50
y=100
答:这家食品厂到A地的路程是50km,到B地的路程是100km.
(2)食品厂到A地的铁路路程为50-20=30(km),到B地的铁路路程为100-30=70(km).
设这家食品厂此次收购食材m t,销售食品n t.
根据题意,得
解这个方程组,得
m=220
n=200
1.5×(20m+30n)=15600
1×(30m+70n)=20600
这批食品每吨的售价应为
(863800-15600+20600+220×5000)÷200=10000(元)
答:要想该批食品销售完后工厂共获利863800元,则这批食品每吨的售价应为10000元.
例题 小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
家
学校
举一反三
走平路时间 走上(下)坡时间 合 计
从家到学校
从学校到家
10min
15min
解:设小华家到学校平路长x m,坡路长y m.
解:设小华家到学校平路长x m,坡路长y m.
根据相等关系,得
解这个方程组,得
x=300
y=400
小华家到学校的路程为300+400=700(m)
答:小华家离学校700m远.
从甲地到乙地有一段上坡和一段下坡.如果保持上坡每分钟走50m,下坡每分钟走100m,那么从甲地到乙地需要25 min,从乙地到甲地需要20 min.甲地到乙地全程多少米?
解:设甲地到乙地上坡的路程为x m,下坡的路程为y m.
根据相等关系,得
解这个方程组,得
x=1000
y=500
甲地到乙地的路程为1000+500=1500(m)
答:甲地到乙地全程1500m.
对应练习
A 地至 B 地的航线长 9750 km,一架飞机从 A 地顺风飞往 B 地需 12.5 h,它逆风飞行同样的航线需 13 h,求飞机的平均速度与风速.
解:设飞机的平均速度为 x km/h,风速为 y km/h.
由题意,得 化简,得
①+②,得 2x = 1530.解得 x = 765.
把 x = 765 代入①,得 y = 15.
∴这个方程组的解为
答:飞机的平均速度是765km/h,风速是15km/h.
(x+y)×12.5=9750
(x-y)×13=9750
x+y=780 ①
x-y=750 ②
x=765
y=15
实际问题
数学问题
(二元一次方程组)
实际问题的答案
数学问题的解
(二元一次方程组的解)
设未知数、列方程组
转化
检验
解方程组
代入法
加减法
(消元)
课堂小结
二元一次方程组
消元——解二元一次方程组
实际问题与二元一次方程组
三元一次方程组的解法
二元一次方程组
代入法
加减法
和差倍分与配套问题
几何问题与图文信息问题
经济问题与行程问题
新课一览
二元一次方程组
实际问题与二元一次方程组
8
第3课时 经济问题与行程问题
人教版·七年级下册
回顾导入
填一填:
(1)某工厂去年的总产值是x万元,今年的总产值比去年增加了20%,则今年的总产值是______________万元;
(2)若该厂去年的总支出是y万元,今年的总支出比去年减少了10%,则今年的总支出是______________万元;
(3)若该厂今年的利润比去年增加了50%,则结合(1)(2)可列方程为_________________________________.
(1+20%)x
(1-10%)y
(1+20%)x-(1-10%)y=(1+50%)(x-y)
探究3
如图,长青化工厂与 A,B 两地有公路、铁路相连.这家工厂从 A 地购买一批每吨1000元的原料运回工厂,制成每吨 8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
产品的销售款-(原料款+运输费)=净利润
自主探究
产品 x t 原料 y t 合 计
公路运费(元)
铁路运费(元)
价值(元)
借助列表分析,确定题目中的数量关系.
1.5×20x
1.2×110x
8000x
1.5×10y
1.2×120y
1000y
1.5×(20x+10y)
1.2×(110x+120y)
等量关系:
①销售款=产品数量×产品单价
②原料费=原料数量×原料单价
③运输费=运价×货物质量×路程
根据上表中运费之间的关系,列出方程组,
因此,这批产品的销售款比原料费与运输费的和多_________元.
1887800
1.5×(20x+10y)=15000
1.2×(110x+120y)=97200
整理,得
2x+y=1000
11x+12y=8100
解这个方程组,得
x=300
y=400
8000×300-1000×400-15000-97200=1887800(元)
对于复杂的实际问题,可以通过列表的方法将所有的数量关系进行整理,发现等量关系,列出方程组.
如图,A,B两地由公路和铁路相连,在这条路上有一家食品厂,它到B地的路程是到A地路程的2倍.该食品厂从A地收购一批食材运回食品厂,全部加工成食品(制作过程中有损耗)运到B地销售,两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.已知公路运费为1.5元/(t. km),铁路运费为1元/(t. km).
(1)这家食品厂到A,B两地的路程分别是多少千米?
(2)若这家食品厂此次收购的食材每吨花费5000元,要想该批食品销售完后.工厂共获利863800元,则这批食品每吨的售价应为多少元?(利润=
总售价-总成本-总运费)
对应练习
解:(1)设这家食品厂到A地的路程是xkm,到B地的路程是ykm.
根据题意,得
x+y=20+100+30
y=2x
解这个方程组,得
x=50
y=100
答:这家食品厂到A地的路程是50km,到B地的路程是100km.
(2)食品厂到A地的铁路路程为50-20=30(km),到B地的铁路路程为100-30=70(km).
设这家食品厂此次收购食材m t,销售食品n t.
根据题意,得
解这个方程组,得
m=220
n=200
1.5×(20m+30n)=15600
1×(30m+70n)=20600
这批食品每吨的售价应为
(863800-15600+20600+220×5000)÷200=10000(元)
答:要想该批食品销售完后工厂共获利863800元,则这批食品每吨的售价应为10000元.
例题 小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
家
学校
举一反三
走平路时间 走上(下)坡时间 合 计
从家到学校
从学校到家
10min
15min
解:设小华家到学校平路长x m,坡路长y m.
解:设小华家到学校平路长x m,坡路长y m.
根据相等关系,得
解这个方程组,得
x=300
y=400
小华家到学校的路程为300+400=700(m)
答:小华家离学校700m远.
从甲地到乙地有一段上坡和一段下坡.如果保持上坡每分钟走50m,下坡每分钟走100m,那么从甲地到乙地需要25 min,从乙地到甲地需要20 min.甲地到乙地全程多少米?
解:设甲地到乙地上坡的路程为x m,下坡的路程为y m.
根据相等关系,得
解这个方程组,得
x=1000
y=500
甲地到乙地的路程为1000+500=1500(m)
答:甲地到乙地全程1500m.
对应练习
A 地至 B 地的航线长 9750 km,一架飞机从 A 地顺风飞往 B 地需 12.5 h,它逆风飞行同样的航线需 13 h,求飞机的平均速度与风速.
解:设飞机的平均速度为 x km/h,风速为 y km/h.
由题意,得 化简,得
①+②,得 2x = 1530.解得 x = 765.
把 x = 765 代入①,得 y = 15.
∴这个方程组的解为
答:飞机的平均速度是765km/h,风速是15km/h.
(x+y)×12.5=9750
(x-y)×13=9750
x+y=780 ①
x-y=750 ②
x=765
y=15
实际问题
数学问题
(二元一次方程组)
实际问题的答案
数学问题的解
(二元一次方程组的解)
设未知数、列方程组
转化
检验
解方程组
代入法
加减法
(消元)
课堂小结
