最新人教版七下数学 9.1.2 不等式的性质 课件(共27张PPT)
文档属性
| 名称 | 最新人教版七下数学 9.1.2 不等式的性质 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 16:54:29 | ||
图片预览








文档简介
(共27张PPT)
9.1 不等式
9.1.2 不等式的性质
R·七年级数学下册
1.通过类比、猜测、验证发现不等式的性质,并掌握不等式的性质.
2.初步体会不等式与等式的异同.
3.会运用不等式的性质解决简单的问题.
学习目标
复习回顾
回想一下,等式有哪些性质?分别用文字语言和符号语言表示出来.
等式的性质 文字语言 符号语言
性质1 等式两边加(或减)同一个数(或式子),结果仍相等 如果a=b,那么a±c=b±c
性质2 等式两边同时乘一个数,或除以同一个不为0的数,结果仍相等 如果a=b,那么ac=bc,如果a=b(c≠0),那么
不等式有没有类似的性质?
新课探究
探究1 不等式的性质
用“>”或“<”填空,并总结其中的规律:
思考
(1)5 > 3,
① 5+2 ______ 3+2.
② 5 - 2 ______ 3 - 2.
(2)-1 < 3,
① -1+2 ______ 3+2.
② -1-3 ______ 3 - 3.
>
>
<
<
发现:当不等式两边加或减同一个数(正数或负数)时,不等号的方向________.
不变
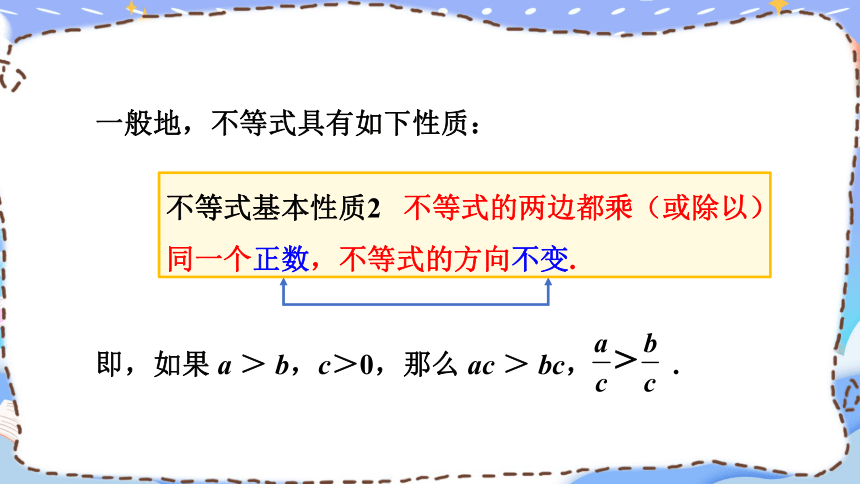
一般地,不等式具有如下性质:
不等式基本性质1 不等式的两边都加上(或都减去)同一个数或(式),不等式的方向不变.
即,如果 a > b,那么 a + c > b + c,且 a – c > b - c.
用“>”或“<”填空,并总结其中的规律:
(3)6 > 3,
① 6×5 ______ 2×5.
② 6÷5 ______ 2÷5.
(4)-2 < 3,
① -2×6 ______ 3×6.
② -2÷6 ______ 3÷6.
>
<
思考
发现:当不等式两边乘(或除以)同一个正数时,不等号的方向________.
不变
>
<
一般地,不等式具有如下性质:
不等式基本性质2 不等式的两边都乘(或除以)同一个正数,不等式的方向不变.
即,如果 a > b,c>0,那么 ac > bc, .
(3)6 > 3,
① 6×5 ______ 2×5.
② 6÷5 ______ 2÷5.
③6×(-5) ______ 2×(-5).
④ 6÷(-5) ______ 2÷(-5).
(4)-2 < 3,
① -2×6 ______ 3×6.
② -2÷6 ______ 3÷6.
③ - 2×(-6) ______ 3×(-6).
④ -2÷(-6) ______ 3÷(-6).
>
<
发现:当不等式两边乘(或除以)同一个负数时,不等号的方向________.
改变
>
<
<
<
>
>
用“>”或“<”填空,并总结其中的规律:
思考
一般地,不等式具有如下性质:
不等式基本性质3 不等式的两边都乘(或除以)同一个负数,不等式的方向改变.
即,如果 a > b,c<0,那么 ac < bc, .
不等式性质2
不等式性质3
不等式两边乘(或除以)同一个正数,不等号方向不变。
不等式两边乘(或除以)同一个负数,不等号方向改变。
如果 a > b,c > 0,那么 ac > bc(或 )
如果 a > b,c < 0,那么 ac < bc(或 )
不等式性质2和不等式性质3有什么区别?
对于乘法(或除法)运算,不等式性质要乘(或除)的数正负不同,结果也不同.
不等式的性质与等式的性质的不同点和相同点:
类别 不同点 相同点
不等式
等式 两边乘(或除以)同一个负数时,大小关系改变
两边乘(或除以)同一个负数时,相等关系不变
1.两边加(或减)同一个数(或式子)时,不等式两边的大小关系和等式两边的相等关系都不变;
2.两边乘(或除以)同一个正数时,不等式两边的大小关系和等式两边的相等关系都不变
<针对训练>
1. 设a>b,用“<”或“>”填空:
(1)a+2_____b+2; (2)a-3_____b-3;
(3)-4a_____-4b; (4)
<
>
>
>
【教材P117 练习】
2. 根据不等式的性质,下列变形正确的是( )
由 a>b 得 ac2>bc2
由 ac2>bc2 得 a>b
由 >2 得 a<2
由 2x+1>x 得 x<-1
B
例1 利用不等式的性质解下列不等式:
(1)x-7>26;(2)3x<2x+1
(3) x>50 (4)-4x>3
【教材P117 例1】
探究2 利用不等式的性质解简单的不等式
解未知数为x的不等式
化为x>a或x<a的形式
目标
思路:
方法:不等式基本性质1~3
(1)x-7>26
x-7+7>26+7
x>33
0
33
用数轴表示为
(不等式的性质1)
(2)3x<2x+1
3x-2x<2x+1-2x
x<1
用数轴表示为
0
1
(不等式的性质1)
(3) x>50
x>75
× x> ×50
0
75
用数轴表示为
(不等式的性质2)
(4)-4x>3
用数轴表示为
0
(不等式的性质3)
下面是某同学根据不等式的性质做的一道题:
在不等式 -4x + 5 > 9 的两边都减去 5,得
-4x > 4.
在不等式 -4x > 4 的两边都除以 -4,得
x > -1.
请问他做对了吗?如果不对,请改正.
x < -1
<针对训练>
符号“≥” 与“>”的意思有什么区别 “≤”与“<”呢
符号“≥”和“≤”分别比“>”和“<”各多了一层相等的含义,它们是不等号与等号的合写形式.
为了表示2011年9月1日北京的最低气温是19 ℃,最高气温是28 ℃,我们可以用t表示这天的气温,t是随时间变化的,但是它有一定的变化范围,即t ≥ 19℃并且t ≤ 28 ℃.
t ≥ 19℃
t ≤ 28 ℃
为了表示2011年9月1日北京的最低气温是19 ℃,最高气温是28 ℃,我们可以用t表示这天的气温,t是随时间变化的,但是它有一定的变化范围,即t ≥ 19℃并且t ≤ 28 ℃.
t ≥ 19℃
t ≤ 28 ℃
符号“≥”读作“大于或等于”,也可说是“不小于”
符号“≤”读作“小于或等于”,也可说是“不大于”
用数轴表示不等式的解集时,实心圆点和空心圆圈有什么区别 不等式的解集中含“≥”“≤”时在数轴上如何表示
实心圆点表示取值范围内包含这个数,而空心圆圈则表示不包含这个数.
不等式的解集 用数轴表示 注意
x ≥ a 端点用实心圆,方向向右
x ≤ a 端点用实心圆,方向向左
a
a
例 2 某长方体形状的容器长 5 cm,宽 3 cm,高 10 cm,容器内原有水的高度为 3 cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出 V 的取值范围.
探究3 利用不等式的性质解决实际问题
【教材P119 例2】
【分析】
V新注入水 + V原有水 ≤ V容器,
体积不能为负数→V新注入水 ≥ 0.
3cm
V新注入水 + V原有水 ≤ V容器,
同时体积不能为负数→V新注入水 ≥ 0.
V新注入水 + 3×5×3 ≤ 3×5×10
3cm
V新注入水 + 45 ≤ 150
V新注入水 ≤ 105
0 ≤
在数轴上怎么表示?
0
105
注意:这是一个包含两端点的区间(闭区间)
<针对训练>
用炸药爆破时,如果导火索燃烧的速度是0.8 cm/s,人跑开的速度是4 m/s,为了让点导火索的战士在爆破时能够跑到100 m以外(不含100 m)的安全区域,这个导火索的长度应大于多少厘米?请将解集在数轴上表示出来.
解:设导火索的长度是x cm.
根据题意,得 ,解得x > 20.
故导火索的长度应大于20 cm.
在数轴上表示x的取值范围如图所示.
0
20
随堂演练
1. 用不等式的性质解下列不等式,并在数轴上表示解集:
【教材P119 练习 第1题】
x>-6
-6
0
用数轴表示为
(不等式的性质1)
x < -5
-5
0
用数轴表示为
(不等式的性质1)
x<6
0
6
用数轴表示为
(不等式的性质3)
用数轴表示为
(不等式的性质2)
x+5-5>-1-5
4x-3x < 3x-5-3x
-8x÷(-8) < 10÷(-8)
0
2. 用不等式表示下列语句并写出解集,并在数轴上表示解集:
【教材P119 练习 第2题】
(1)x的3倍大于或等于1; (2)x与3的和不小于6;
(3)y与1的差不大于0; (4)y的 小于或等于-2.
解:(1)3x ≥ 1
用数轴表示为
0
(2)x+3 ≥ 6
x ≥ 3
用数轴表示为
0
3
2. 用不等式表示下列语句并写出解集,并在数轴上表示解集:
【教材P119 练习 第2题】
(1)x的3倍大于或等于1; (2)x与3的和不小于6;
(3)y与1的差不大于0; (4)y的 小于或等于-2.
(3)y-1 ≤ 0
用数轴表示为
(4)
x ≤ -8
用数轴表示为
y ≤ 1
0
1
0
-8
课堂小结
不等式的基本性质
不等式的基本性质1
不等式的基本性质2
不等式的基本性质3
如果 a>b,那么
a ± c > b ± c
如果 a>b,c > 0, 那么
ac > bc(或 )
如果 a>b, c < 0,那么
ac < bc(或 )
应用
9.1 不等式
9.1.2 不等式的性质
R·七年级数学下册
1.通过类比、猜测、验证发现不等式的性质,并掌握不等式的性质.
2.初步体会不等式与等式的异同.
3.会运用不等式的性质解决简单的问题.
学习目标
复习回顾
回想一下,等式有哪些性质?分别用文字语言和符号语言表示出来.
等式的性质 文字语言 符号语言
性质1 等式两边加(或减)同一个数(或式子),结果仍相等 如果a=b,那么a±c=b±c
性质2 等式两边同时乘一个数,或除以同一个不为0的数,结果仍相等 如果a=b,那么ac=bc,如果a=b(c≠0),那么
不等式有没有类似的性质?
新课探究
探究1 不等式的性质
用“>”或“<”填空,并总结其中的规律:
思考
(1)5 > 3,
① 5+2 ______ 3+2.
② 5 - 2 ______ 3 - 2.
(2)-1 < 3,
① -1+2 ______ 3+2.
② -1-3 ______ 3 - 3.
>
>
<
<
发现:当不等式两边加或减同一个数(正数或负数)时,不等号的方向________.
不变
一般地,不等式具有如下性质:
不等式基本性质1 不等式的两边都加上(或都减去)同一个数或(式),不等式的方向不变.
即,如果 a > b,那么 a + c > b + c,且 a – c > b - c.
用“>”或“<”填空,并总结其中的规律:
(3)6 > 3,
① 6×5 ______ 2×5.
② 6÷5 ______ 2÷5.
(4)-2 < 3,
① -2×6 ______ 3×6.
② -2÷6 ______ 3÷6.
>
<
思考
发现:当不等式两边乘(或除以)同一个正数时,不等号的方向________.
不变
>
<
一般地,不等式具有如下性质:
不等式基本性质2 不等式的两边都乘(或除以)同一个正数,不等式的方向不变.
即,如果 a > b,c>0,那么 ac > bc, .
(3)6 > 3,
① 6×5 ______ 2×5.
② 6÷5 ______ 2÷5.
③6×(-5) ______ 2×(-5).
④ 6÷(-5) ______ 2÷(-5).
(4)-2 < 3,
① -2×6 ______ 3×6.
② -2÷6 ______ 3÷6.
③ - 2×(-6) ______ 3×(-6).
④ -2÷(-6) ______ 3÷(-6).
>
<
发现:当不等式两边乘(或除以)同一个负数时,不等号的方向________.
改变
>
<
<
<
>
>
用“>”或“<”填空,并总结其中的规律:
思考
一般地,不等式具有如下性质:
不等式基本性质3 不等式的两边都乘(或除以)同一个负数,不等式的方向改变.
即,如果 a > b,c<0,那么 ac < bc, .
不等式性质2
不等式性质3
不等式两边乘(或除以)同一个正数,不等号方向不变。
不等式两边乘(或除以)同一个负数,不等号方向改变。
如果 a > b,c > 0,那么 ac > bc(或 )
如果 a > b,c < 0,那么 ac < bc(或 )
不等式性质2和不等式性质3有什么区别?
对于乘法(或除法)运算,不等式性质要乘(或除)的数正负不同,结果也不同.
不等式的性质与等式的性质的不同点和相同点:
类别 不同点 相同点
不等式
等式 两边乘(或除以)同一个负数时,大小关系改变
两边乘(或除以)同一个负数时,相等关系不变
1.两边加(或减)同一个数(或式子)时,不等式两边的大小关系和等式两边的相等关系都不变;
2.两边乘(或除以)同一个正数时,不等式两边的大小关系和等式两边的相等关系都不变
<针对训练>
1. 设a>b,用“<”或“>”填空:
(1)a+2_____b+2; (2)a-3_____b-3;
(3)-4a_____-4b; (4)
<
>
>
>
【教材P117 练习】
2. 根据不等式的性质,下列变形正确的是( )
由 a>b 得 ac2>bc2
由 ac2>bc2 得 a>b
由 >2 得 a<2
由 2x+1>x 得 x<-1
B
例1 利用不等式的性质解下列不等式:
(1)x-7>26;(2)3x<2x+1
(3) x>50 (4)-4x>3
【教材P117 例1】
探究2 利用不等式的性质解简单的不等式
解未知数为x的不等式
化为x>a或x<a的形式
目标
思路:
方法:不等式基本性质1~3
(1)x-7>26
x-7+7>26+7
x>33
0
33
用数轴表示为
(不等式的性质1)
(2)3x<2x+1
3x-2x<2x+1-2x
x<1
用数轴表示为
0
1
(不等式的性质1)
(3) x>50
x>75
× x> ×50
0
75
用数轴表示为
(不等式的性质2)
(4)-4x>3
用数轴表示为
0
(不等式的性质3)
下面是某同学根据不等式的性质做的一道题:
在不等式 -4x + 5 > 9 的两边都减去 5,得
-4x > 4.
在不等式 -4x > 4 的两边都除以 -4,得
x > -1.
请问他做对了吗?如果不对,请改正.
x < -1
<针对训练>
符号“≥” 与“>”的意思有什么区别 “≤”与“<”呢
符号“≥”和“≤”分别比“>”和“<”各多了一层相等的含义,它们是不等号与等号的合写形式.
为了表示2011年9月1日北京的最低气温是19 ℃,最高气温是28 ℃,我们可以用t表示这天的气温,t是随时间变化的,但是它有一定的变化范围,即t ≥ 19℃并且t ≤ 28 ℃.
t ≥ 19℃
t ≤ 28 ℃
为了表示2011年9月1日北京的最低气温是19 ℃,最高气温是28 ℃,我们可以用t表示这天的气温,t是随时间变化的,但是它有一定的变化范围,即t ≥ 19℃并且t ≤ 28 ℃.
t ≥ 19℃
t ≤ 28 ℃
符号“≥”读作“大于或等于”,也可说是“不小于”
符号“≤”读作“小于或等于”,也可说是“不大于”
用数轴表示不等式的解集时,实心圆点和空心圆圈有什么区别 不等式的解集中含“≥”“≤”时在数轴上如何表示
实心圆点表示取值范围内包含这个数,而空心圆圈则表示不包含这个数.
不等式的解集 用数轴表示 注意
x ≥ a 端点用实心圆,方向向右
x ≤ a 端点用实心圆,方向向左
a
a
例 2 某长方体形状的容器长 5 cm,宽 3 cm,高 10 cm,容器内原有水的高度为 3 cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出 V 的取值范围.
探究3 利用不等式的性质解决实际问题
【教材P119 例2】
【分析】
V新注入水 + V原有水 ≤ V容器,
体积不能为负数→V新注入水 ≥ 0.
3cm
V新注入水 + V原有水 ≤ V容器,
同时体积不能为负数→V新注入水 ≥ 0.
V新注入水 + 3×5×3 ≤ 3×5×10
3cm
V新注入水 + 45 ≤ 150
V新注入水 ≤ 105
0 ≤
在数轴上怎么表示?
0
105
注意:这是一个包含两端点的区间(闭区间)
<针对训练>
用炸药爆破时,如果导火索燃烧的速度是0.8 cm/s,人跑开的速度是4 m/s,为了让点导火索的战士在爆破时能够跑到100 m以外(不含100 m)的安全区域,这个导火索的长度应大于多少厘米?请将解集在数轴上表示出来.
解:设导火索的长度是x cm.
根据题意,得 ,解得x > 20.
故导火索的长度应大于20 cm.
在数轴上表示x的取值范围如图所示.
0
20
随堂演练
1. 用不等式的性质解下列不等式,并在数轴上表示解集:
【教材P119 练习 第1题】
x>-6
-6
0
用数轴表示为
(不等式的性质1)
x < -5
-5
0
用数轴表示为
(不等式的性质1)
x<6
0
6
用数轴表示为
(不等式的性质3)
用数轴表示为
(不等式的性质2)
x+5-5>-1-5
4x-3x < 3x-5-3x
-8x÷(-8) < 10÷(-8)
0
2. 用不等式表示下列语句并写出解集,并在数轴上表示解集:
【教材P119 练习 第2题】
(1)x的3倍大于或等于1; (2)x与3的和不小于6;
(3)y与1的差不大于0; (4)y的 小于或等于-2.
解:(1)3x ≥ 1
用数轴表示为
0
(2)x+3 ≥ 6
x ≥ 3
用数轴表示为
0
3
2. 用不等式表示下列语句并写出解集,并在数轴上表示解集:
【教材P119 练习 第2题】
(1)x的3倍大于或等于1; (2)x与3的和不小于6;
(3)y与1的差不大于0; (4)y的 小于或等于-2.
(3)y-1 ≤ 0
用数轴表示为
(4)
x ≤ -8
用数轴表示为
y ≤ 1
0
1
0
-8
课堂小结
不等式的基本性质
不等式的基本性质1
不等式的基本性质2
不等式的基本性质3
如果 a>b,那么
a ± c > b ± c
如果 a>b,c > 0, 那么
ac > bc(或 )
如果 a>b, c < 0,那么
ac < bc(或 )
应用
