第十六章 二次根式 单元检测卷(含解析) 人教版八年级数学下册
文档属性
| 名称 | 第十六章 二次根式 单元检测卷(含解析) 人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 69.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 16:01:59 | ||
图片预览



文档简介
第十六章 二次根式 单元检测卷 人教版八年级数学下册
一、选择题
1.代数式中x的取值范围是( )
A.x≥-4 B.x>2 C.x≥-4且x≠2 D.x>-4且x≠2
2.下列式子:①()2=19;②()2=-19;③()2=a-b;④a=-( )2(a≤0).其中一定正确的个数为( )
A.1 B.2 C.3 D.4
3.下列计算正确的是( )
A.=±4 B.±=3 C.=-3 D.()2=3
4.下列二次根式中,属于最简二次根式的是 ( )
A. B. C. D.
5.已知a=+,b=-,则a与b的关系为( )
A.互为相反数 B.互为倒数
C.相等 D.a是b的算术平方根
6.已知则代数式的值是( )
A.9 B.±3 C.3 D.5
7.若 的整数部分为a,小数部分为b,则代数式 的值为 ( )
A.-2 B.0 C.1 D.2
8.按如图所示运算程序,输入,,则输出结果为( )
A. B.6 C. D.
二、填空题
9.实数x在数轴上的对应点的位置如图所示,则 , 。
10.若111.已知长方形的宽是3 ,它的面积是18 ,则它的长是 .
12.若与最简二次根式可以合并,则 .
三、计算题
13. 计算:
(1)
(2)
(3)
14.实数 在数轴上的对应点的位置如图所示,化简 .
四、解答题
15.若a,b为实数,且b= ,=a+3,求ab+c的值
16. 已知x,y为实数,且满足,求2x+3y的值.
17.某居民小区有一块形状为长方形的绿地ABCD,长方形绿地的长BC为 m,宽AB为 m,现要在长方形绿地中修建一个长方形 花坛(即图中阴影部分),长方形花坛的长为( +1)m,宽为( -1)m.
(1)长方形ABCD的周长是多少?
(2)除去修建花坛的地方,其他地方全修建成通道,通道上要铺上造价为5元/m2的地砖,要铺完整个通道,则购买地砖需要花费多少元?(结果化为最简二次根式)
18.有一块长方形木板,木工采用如图所示的方式,在木板上截出两个面积分别为18dm 和32dm 的正方形木板.
(1)求剩余木板的面积.
(2)若木工想从剩余的木板中截出长为 1.5d m、宽为 1 dm的长方形木条,则最多能 截出 块.
19.已知长方形的长宽
(1)求长方形的周长.
(2)求与长方形等面积的正方形的周长,并比较长方形的周长与正方形的周长的大小关系.
20.已知的整数部分为a,小数部分为b,求(3a+b)(3a-b)的值.
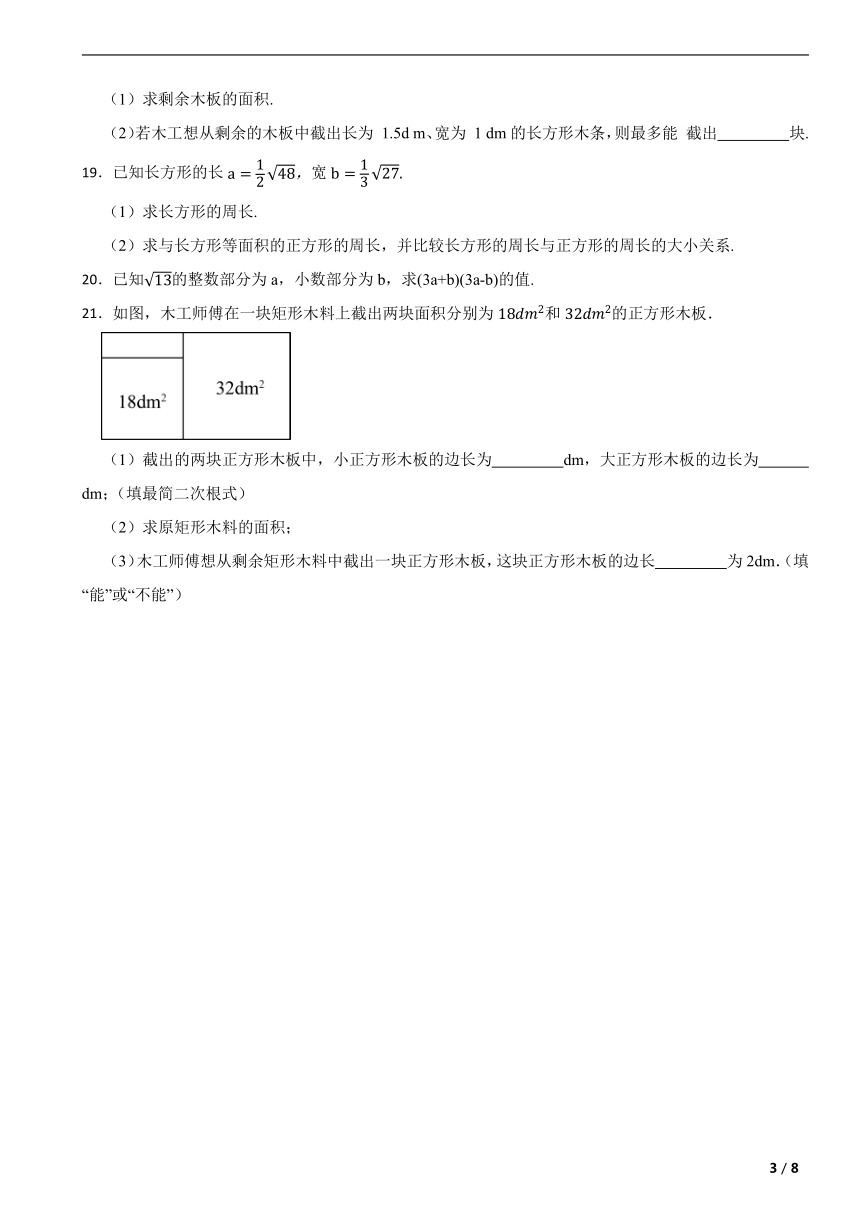
21.如图,木工师傅在一块矩形木料上截出两块面积分别为和的正方形木板.
(1)截出的两块正方形木板中,小正方形木板的边长为 dm,大正方形木板的边长为 dm;(填最简二次根式)
(2)求原矩形木料的面积;
(3)木工师傅想从剩余矩形木料中截出一块正方形木板,这块正方形木板的边长 为2dm.(填“能”或“不能”)
答案解析部分
1.【答案】C
【解析】【解答】解:要使 有意义,
只需x+4≥0且 x-2≠0,
解得x≥-4且x≠2.
故答案为:C.
【分析】根据二次根式的被开方数不能为负数及分式的分母不能为零,列出不等式(组)求解.
2.【答案】B
【解析】【解答】解: ①()2=19,故正确;
②()2中根号内是负数,无意义,故错误;
③()2=a-b 成立的前提是a-b≥0,故错误;
④因为a≤0 ,所以-( )2=-(-a)=a,故正确,
综上所述,正确的有①④,共2个.
故答案为:B.
【分析】利用()2=a(a≥0)求解.
3.【答案】D
【解析】【解答】解:A、 =4,故选项A错误;
B、±=±3,故选项B错误;
C、=3,故选项C错误;
D、()2=3,故选项D正确 .
故答案为:D.
【分析】根据算术平方根求解可判断A选项;根据平方根求解可判断B选项;根据可判断C选项;根据可判断D选项.
4.【答案】A
【解析】【解答】解:A、是最简二次根式,故选项A正确;
B、,故不是最简二次根式,故选项B错误;
C、,故不是最简二次根式,故选项C错误;
D、,故不是最简二次根式,故选项D错误.
故答案为:A.
【分析】本题考查了最简二次根式的知识.最简二次根式必须满足两个条件:①被开方数不含分母;②被开方数不含能开得尽方的因数或因式,据此逐个判断得出答案.
5.【答案】B
6.【答案】C
7.【答案】D
【解析】【解答】解:∵,
∴
∴,
∵的整数部分为a,小数部分为b ,
∴,,
∴.
故答案为:D.
【分析】根据估算无理数大小可得,进而根据不等式性质可得,则可求得a、b的值,最后根据平方差公式及二次根式的混合运算法则可求得代数式的值.
8.【答案】A
【解析】【解答】解:∵,即x>y,
∴,
故答案为:A.
【分析】先判断出,再将x、y的值代入计算即可.
9.【答案】-x;-x
【解析】【解答】解:由题意得,
∴
故答案为:-x;-x.
【分析】由数轴可得到,再根据二次根式的性质,进行逐一计算判断即可.
10.【答案】1
【解析】【解答】解:因为,
所以,
所以
因为,
所以,
故
所以 =
故答案为:1.
【分析】本题主要考查了二次根式的化简与运算. 首先根据可得到:,,根据,可对进行化简,进而再几何绝对值性质化简后合并同类项即可.
11.【答案】6
【解析】【解答】解:∵长方形的宽是3 ,它的面积是18 ,
∴它的长是:18 ÷3 =6 .
故答案为:6 .
【分析】直接利用二次根式的除法运算法则计算得出答案.
12.【答案】3
13.【答案】(1)
(2)-2
(3)
14.【答案】0
15.【答案】解:由题意得
解得a=1.
∴b=,4.
∴c=±4,
当c=4时,原式=,
当c=-4时原式=
综上所述,ab+c的值为或.
【解析】【分析】先根据二次根式的被开方数不能为负数及分式的分母不能为零列出不等式组,可求出a的值,进而代入求得b,c的值,再将a、b、c得值代入待求式子,根据有理数的加减乘除混合运算的运算顺序计算即可求值.
16.【答案】
17.【答案】(1)解:长方形ABCD的周长=m,
即长方形ABCD的周长是m.
(2)解:购买地砖需要花费5×= 元,
即购买地砖需要花费元.
【解析】【分析】(1)根据长方形的周长公式列出式子,化简即可;
(2)将造价乘以面积,再化简.
18.【答案】(1)解:右边正方形的边长为,左下角正方形的边长为,
∴整个矩形的长为,宽为,
∴剩余木料的面积;
(2)2
【解析】【解答】解:(2)剩余木条的长为,宽为,
∵,,
∴能截出个木条.
故答案为:2.
【分析】(1)首先根据算术平方根求出两个正方形的边长,再求出大矩形的长与宽,进而利用长方形的面积减去两个正方形的面积即可得到答案;
(2)先计算剩余木条的长与宽,再利用,,从而可得答案.
19.【答案】(1)6
(2)4,长方形的周长大于正方形的周长
20.【答案】
21.【答案】(1);
(2)解:原矩形木料的长为,宽为,
,
原矩形木料的面积为;
(3)不能
【解析】【解答】解:小正方形木板的边长为:
大正方形木板的边长为
故答案为:,.
(3)剩余矩形木料的长为,宽为
而
∴这块正方形木板的边长不能为2dm.
故答案为:不能.
【分析】(1)根据正方形的面积即可求得边长;
(2)根据题意求得长为,宽为,根据矩形的性质求面即可求解;
(3)求得剩余矩形木料的长和宽,结合题意,即可求解.
1 / 1
一、选择题
1.代数式中x的取值范围是( )
A.x≥-4 B.x>2 C.x≥-4且x≠2 D.x>-4且x≠2
2.下列式子:①()2=19;②()2=-19;③()2=a-b;④a=-( )2(a≤0).其中一定正确的个数为( )
A.1 B.2 C.3 D.4
3.下列计算正确的是( )
A.=±4 B.±=3 C.=-3 D.()2=3
4.下列二次根式中,属于最简二次根式的是 ( )
A. B. C. D.
5.已知a=+,b=-,则a与b的关系为( )
A.互为相反数 B.互为倒数
C.相等 D.a是b的算术平方根
6.已知则代数式的值是( )
A.9 B.±3 C.3 D.5
7.若 的整数部分为a,小数部分为b,则代数式 的值为 ( )
A.-2 B.0 C.1 D.2
8.按如图所示运算程序,输入,,则输出结果为( )
A. B.6 C. D.
二、填空题
9.实数x在数轴上的对应点的位置如图所示,则 , 。
10.若1
12.若与最简二次根式可以合并,则 .
三、计算题
13. 计算:
(1)
(2)
(3)
14.实数 在数轴上的对应点的位置如图所示,化简 .
四、解答题
15.若a,b为实数,且b= ,=a+3,求ab+c的值
16. 已知x,y为实数,且满足,求2x+3y的值.
17.某居民小区有一块形状为长方形的绿地ABCD,长方形绿地的长BC为 m,宽AB为 m,现要在长方形绿地中修建一个长方形 花坛(即图中阴影部分),长方形花坛的长为( +1)m,宽为( -1)m.
(1)长方形ABCD的周长是多少?
(2)除去修建花坛的地方,其他地方全修建成通道,通道上要铺上造价为5元/m2的地砖,要铺完整个通道,则购买地砖需要花费多少元?(结果化为最简二次根式)
18.有一块长方形木板,木工采用如图所示的方式,在木板上截出两个面积分别为18dm 和32dm 的正方形木板.
(1)求剩余木板的面积.
(2)若木工想从剩余的木板中截出长为 1.5d m、宽为 1 dm的长方形木条,则最多能 截出 块.
19.已知长方形的长宽
(1)求长方形的周长.
(2)求与长方形等面积的正方形的周长,并比较长方形的周长与正方形的周长的大小关系.
20.已知的整数部分为a,小数部分为b,求(3a+b)(3a-b)的值.
21.如图,木工师傅在一块矩形木料上截出两块面积分别为和的正方形木板.
(1)截出的两块正方形木板中,小正方形木板的边长为 dm,大正方形木板的边长为 dm;(填最简二次根式)
(2)求原矩形木料的面积;
(3)木工师傅想从剩余矩形木料中截出一块正方形木板,这块正方形木板的边长 为2dm.(填“能”或“不能”)
答案解析部分
1.【答案】C
【解析】【解答】解:要使 有意义,
只需x+4≥0且 x-2≠0,
解得x≥-4且x≠2.
故答案为:C.
【分析】根据二次根式的被开方数不能为负数及分式的分母不能为零,列出不等式(组)求解.
2.【答案】B
【解析】【解答】解: ①()2=19,故正确;
②()2中根号内是负数,无意义,故错误;
③()2=a-b 成立的前提是a-b≥0,故错误;
④因为a≤0 ,所以-( )2=-(-a)=a,故正确,
综上所述,正确的有①④,共2个.
故答案为:B.
【分析】利用()2=a(a≥0)求解.
3.【答案】D
【解析】【解答】解:A、 =4,故选项A错误;
B、±=±3,故选项B错误;
C、=3,故选项C错误;
D、()2=3,故选项D正确 .
故答案为:D.
【分析】根据算术平方根求解可判断A选项;根据平方根求解可判断B选项;根据可判断C选项;根据可判断D选项.
4.【答案】A
【解析】【解答】解:A、是最简二次根式,故选项A正确;
B、,故不是最简二次根式,故选项B错误;
C、,故不是最简二次根式,故选项C错误;
D、,故不是最简二次根式,故选项D错误.
故答案为:A.
【分析】本题考查了最简二次根式的知识.最简二次根式必须满足两个条件:①被开方数不含分母;②被开方数不含能开得尽方的因数或因式,据此逐个判断得出答案.
5.【答案】B
6.【答案】C
7.【答案】D
【解析】【解答】解:∵,
∴
∴,
∵的整数部分为a,小数部分为b ,
∴,,
∴.
故答案为:D.
【分析】根据估算无理数大小可得,进而根据不等式性质可得,则可求得a、b的值,最后根据平方差公式及二次根式的混合运算法则可求得代数式的值.
8.【答案】A
【解析】【解答】解:∵,即x>y,
∴,
故答案为:A.
【分析】先判断出,再将x、y的值代入计算即可.
9.【答案】-x;-x
【解析】【解答】解:由题意得,
∴
故答案为:-x;-x.
【分析】由数轴可得到,再根据二次根式的性质,进行逐一计算判断即可.
10.【答案】1
【解析】【解答】解:因为,
所以,
所以
因为,
所以,
故
所以 =
故答案为:1.
【分析】本题主要考查了二次根式的化简与运算. 首先根据可得到:,,根据,可对进行化简,进而再几何绝对值性质化简后合并同类项即可.
11.【答案】6
【解析】【解答】解:∵长方形的宽是3 ,它的面积是18 ,
∴它的长是:18 ÷3 =6 .
故答案为:6 .
【分析】直接利用二次根式的除法运算法则计算得出答案.
12.【答案】3
13.【答案】(1)
(2)-2
(3)
14.【答案】0
15.【答案】解:由题意得
解得a=1.
∴b=,4.
∴c=±4,
当c=4时,原式=,
当c=-4时原式=
综上所述,ab+c的值为或.
【解析】【分析】先根据二次根式的被开方数不能为负数及分式的分母不能为零列出不等式组,可求出a的值,进而代入求得b,c的值,再将a、b、c得值代入待求式子,根据有理数的加减乘除混合运算的运算顺序计算即可求值.
16.【答案】
17.【答案】(1)解:长方形ABCD的周长=m,
即长方形ABCD的周长是m.
(2)解:购买地砖需要花费5×= 元,
即购买地砖需要花费元.
【解析】【分析】(1)根据长方形的周长公式列出式子,化简即可;
(2)将造价乘以面积,再化简.
18.【答案】(1)解:右边正方形的边长为,左下角正方形的边长为,
∴整个矩形的长为,宽为,
∴剩余木料的面积;
(2)2
【解析】【解答】解:(2)剩余木条的长为,宽为,
∵,,
∴能截出个木条.
故答案为:2.
【分析】(1)首先根据算术平方根求出两个正方形的边长,再求出大矩形的长与宽,进而利用长方形的面积减去两个正方形的面积即可得到答案;
(2)先计算剩余木条的长与宽,再利用,,从而可得答案.
19.【答案】(1)6
(2)4,长方形的周长大于正方形的周长
20.【答案】
21.【答案】(1);
(2)解:原矩形木料的长为,宽为,
,
原矩形木料的面积为;
(3)不能
【解析】【解答】解:小正方形木板的边长为:
大正方形木板的边长为
故答案为:,.
(3)剩余矩形木料的长为,宽为
而
∴这块正方形木板的边长不能为2dm.
故答案为:不能.
【分析】(1)根据正方形的面积即可求得边长;
(2)根据题意求得长为,宽为,根据矩形的性质求面即可求解;
(3)求得剩余矩形木料的长和宽,结合题意,即可求解.
1 / 1
