1.5平方差公式第1课时-2023-2024学年七年级数学下册同步课件(北师大版)
文档属性
| 名称 | 1.5平方差公式第1课时-2023-2024学年七年级数学下册同步课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 449.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
第1课时
北师大版 数学 七年级下册
5 平方差公式
第一章 整式的乘除
学习目标
1.理解并掌握平方差公式的推导和应用.(重点)
2.理解平方差公式的结构特征,并能运用公式进行简单的运算.(难点)
一、导入新课
复习回顾
1.多项式乘多项式法则:
多项式与多项式相乘,先用一个多项式的 分别乘以另一个多项式的 ,再把所得的积 .
即 =am+an+bm+bn.
每一项
每一项
相加
2.计算:(1)(2x+3)(-x-1); (2)(-2x+3)2.
(2)原式=(-2x+3)(-2x+3)
=4x2-6x-6x+9
=4x2-12x+9.
解:(1)原式=-2x2-2x-3x-3
=-2x2-5x-3.
一、导入新课
情境导入
从前,有-个狡猾的地主,把-块边长为a米的正方形土地租给张老汉种植.第二年,他对张老汉说:“我把这块地的-边减少5米,相邻的另-边增加5米,继续租给你,租金不变,你也没有吃亏,你看如何 ”张老汉-听,觉得好像没有吃亏,就答应道:“好吧.”回到家中,他把这事和邻居们-讲,大家都说:“张老汉,你吃亏了!”他非常吃惊.你知道张老汉是否吃亏了吗
一、导入新课
情境导入
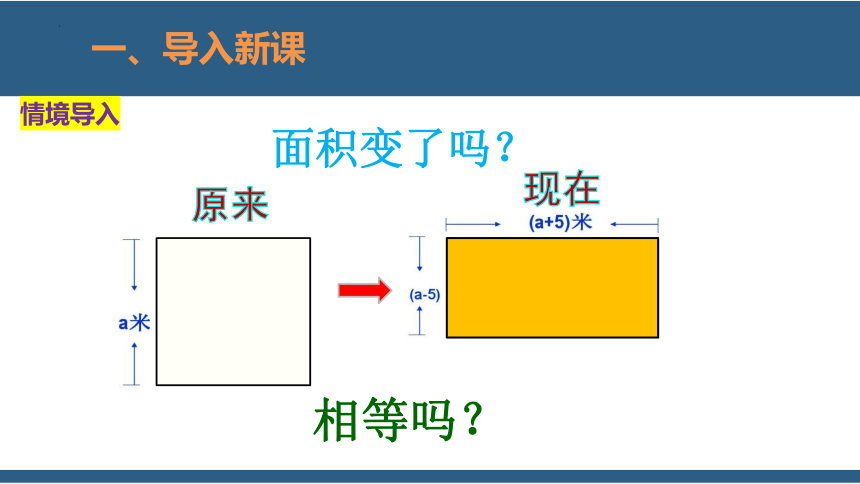
面积变了吗?
原来
现在
相等吗?
二、新知探究
探究:平方差公式
计算下列各题:(1)(x+2)(x-2) ; (2)(1+3a)(1-3a);
(3)(x+5y)(x-5y); (4)(2y+z)(2y-z).
(4)(2y+z)(2y-z)= 4y2 -z2
(2)(1+ 3a)( 1-3a)=1 -9a2
(3)(x+5y)( x-5y)=x2-25y2
(1)(x +2)( x- 2)=x2-4
=x2 - 22
=12-3a2
=x2-(5y)2
=(2y)2-z2
二、新知探究
想一想:观察以上算式及其运算结果,你有什么发现?再举两例验证你的发现.
发现:算式是两个二项式相乘,在这两个二项式中有一项完全相同,另一项互为相反项;算式的运算结果为相同项的平方减去互为相反项的平方.举例略.
二、新知探究
知识归纳
(a+b)(a b)=a2 b2
两数和与这两数差的积,等于这两数的平方差.
平方差公式:
平方差公式的结构特征:
(1)左边是两个二项式的乘积,并且这两个二项式有一项完全相同,另一项互为相反项;
(2)右边是这两项的平方差,即相同项的平方减去相反项的平方.
二、新知探究
1.下列各式中,能用平方差公式进行计算的是 (填写序号).
①(-x-y)(x+y); ②(2x+y)(y-2x);
③(2x+y)(x-2y); ④(-x+y)(x-y);
⑤(a-b+c)(a-b-c).
②⑤
跟踪练习
二、新知探究
2.填一填:
相同项 相反项 结果
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
(a+b)(a-b)
跟踪练习
二、新知探究
平方差公式
注意:1.a表示相同的项,b表示相反的项,与位置无关.
2.这里的a,b既可以表示单项式,也可以表示多项式,或者是更为复杂的代数式.
(a+b)(a-b) = a2-b2
相同为a
相反为b
适当交换
合理加括号
知识归纳
二、新知探究
3.利用平方差公式计算:
(1) (5+6x )( 5-6x ) ; (2) (x-2y)(x+2y);(3) (-m+n)(-m-n)
解:(1)原式=52-(6x)2=25-36x2;
(2)原式=x2-(2y)2=x2 - 4y2;
(3)原式=(-m)2-n2=m2-n2.
跟踪练习
二、新知探究
4.利用平方差公式计算:
(1) (2) (ab+8)(ab-8).
(2)原式=(ab)2-82
=a2b2-64.
跟踪练习
解:(1)原式=
;
二、新知探究
想一想:(a-b)(-a-b)=?你是怎样做的?
解:(a-b)(-a-b)
=(-b+a)(-b-a)
=(-b)2-a2
=b2-a2
变形
应用平方差公式
二、新知探究
平方差公式的计算步骤:
(1)找准公式中的相同项a和相反项b,利用加法交换律调整两个二项式的位置,使之与公式左边对应;
(2)用相同项的平方减去相反项的平方.
知识归纳
三、典例精析
解:(1)(-a+b)(-a-b)
=(-a)2-b2
=a2-b2.
例1 利用平方差公式计算:
(1)(-a+b)(-a-b); (2)(0.25x+y)(-0.25x+y).
(2)(0.25x+y)(-0.25x+y)
=(y+0.25x)·(y-0.25x)
=y2-(0.25x)2
=y2-0.0625x2.
三、典例精析
例2:先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2.
解:(2x-y)(y+2x)-(2y+x)(2y-x)
=4x2-y2- (4y2-x2)
=4x2-y2-4y2+x2
=5x2-5y2.
当x=1,y=2时,
原式=5×12-5×22=-15.
3.计算(-4a-1)(4a-1)的结果为 ( )
A.16a2-1 B.-8a2-1 C.-4a2+1 D.-16a2+1
2.下列各式中不能用平方差公式计算的是( )
A.(x-y)(-x+y) B.(-x+y)(-x-y)
C.(-x-y)(x-y) D.(x+y)(-x+y)
四、当堂练习
1.计算(1+2c)(1-2c)的结果是 ( )
A.4c2-1 B.1-4c2 C.4c2-4c+1 D.1+4c+4c2
B
A
D
6.若a2-b2=,a-b=,则a+b= .
5.对于任意的整数n,能整除(n+3)(n-3)-(n+2)(n-2)的整数是( )
A.4 B.3 C.5 D.2
四、当堂练习
4.若(2-x)(2+x)(4+x2)=16-xn,则n的值等于 ( )
A.6 B.4 C.3 D.2
B
C
7.若(x-ay)(x+ay)=x2-16y2,则a= .
8.一个长方体的池塘长为(4a2+9b2)m,宽为(2a+3b)m,高为(2a-3b)m,则这个池塘的容积是 m3.
±4
(16a4-81b4)
四、当堂练习
(2) (-4x2-3y3)(4x2-3y3)=(-3y3)2-(4x2)2=9y6-16x4.
9.计算:(1)()(); (2)(-4x2-3y3)(4x2-3y3).
四、当堂练习
10.计算:(1)a(1-2a)+2(a+1)(a-1); (2)(2x-3y)(3y+2x)-(4y-3x)(3x+4y);
(3)(-am+bn)(am+bn).
解:(1)原式=a-2a2+2(a2-1)=a-2a2+2a2-2=a-2.
(2)原式=4x2-9y2-16y2+9x2=13x2-25y2.
(3)(-am+bn)(am+bn)=(bn)2-(am)2=b2n-a2m.
四、当堂练习
11.先化简,再求值:(3-x)(3+x)+(x+1)2,其中x=2.
解:原式=9-x2+x2+2x+1
=2x+10.
当x=2时,
原式=2×2+10=14.
五、课堂小结
两个数的和与这两个数的差的积,等于这两个数的平方差.
符号表示:(a+b)(a-b)=a2-b2
紧紧抓住 “一同一反”这一特征.不能直接应用公式的,要经过变形才可以应用.
平方差公式
注意
内容
六、作业布置
习题1.9
第1课时
北师大版 数学 七年级下册
5 平方差公式
第一章 整式的乘除
学习目标
1.理解并掌握平方差公式的推导和应用.(重点)
2.理解平方差公式的结构特征,并能运用公式进行简单的运算.(难点)
一、导入新课
复习回顾
1.多项式乘多项式法则:
多项式与多项式相乘,先用一个多项式的 分别乘以另一个多项式的 ,再把所得的积 .
即 =am+an+bm+bn.
每一项
每一项
相加
2.计算:(1)(2x+3)(-x-1); (2)(-2x+3)2.
(2)原式=(-2x+3)(-2x+3)
=4x2-6x-6x+9
=4x2-12x+9.
解:(1)原式=-2x2-2x-3x-3
=-2x2-5x-3.
一、导入新课
情境导入
从前,有-个狡猾的地主,把-块边长为a米的正方形土地租给张老汉种植.第二年,他对张老汉说:“我把这块地的-边减少5米,相邻的另-边增加5米,继续租给你,租金不变,你也没有吃亏,你看如何 ”张老汉-听,觉得好像没有吃亏,就答应道:“好吧.”回到家中,他把这事和邻居们-讲,大家都说:“张老汉,你吃亏了!”他非常吃惊.你知道张老汉是否吃亏了吗
一、导入新课
情境导入
面积变了吗?
原来
现在
相等吗?
二、新知探究
探究:平方差公式
计算下列各题:(1)(x+2)(x-2) ; (2)(1+3a)(1-3a);
(3)(x+5y)(x-5y); (4)(2y+z)(2y-z).
(4)(2y+z)(2y-z)= 4y2 -z2
(2)(1+ 3a)( 1-3a)=1 -9a2
(3)(x+5y)( x-5y)=x2-25y2
(1)(x +2)( x- 2)=x2-4
=x2 - 22
=12-3a2
=x2-(5y)2
=(2y)2-z2
二、新知探究
想一想:观察以上算式及其运算结果,你有什么发现?再举两例验证你的发现.
发现:算式是两个二项式相乘,在这两个二项式中有一项完全相同,另一项互为相反项;算式的运算结果为相同项的平方减去互为相反项的平方.举例略.
二、新知探究
知识归纳
(a+b)(a b)=a2 b2
两数和与这两数差的积,等于这两数的平方差.
平方差公式:
平方差公式的结构特征:
(1)左边是两个二项式的乘积,并且这两个二项式有一项完全相同,另一项互为相反项;
(2)右边是这两项的平方差,即相同项的平方减去相反项的平方.
二、新知探究
1.下列各式中,能用平方差公式进行计算的是 (填写序号).
①(-x-y)(x+y); ②(2x+y)(y-2x);
③(2x+y)(x-2y); ④(-x+y)(x-y);
⑤(a-b+c)(a-b-c).
②⑤
跟踪练习
二、新知探究
2.填一填:
相同项 相反项 结果
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
(a+b)(a-b)
跟踪练习
二、新知探究
平方差公式
注意:1.a表示相同的项,b表示相反的项,与位置无关.
2.这里的a,b既可以表示单项式,也可以表示多项式,或者是更为复杂的代数式.
(a+b)(a-b) = a2-b2
相同为a
相反为b
适当交换
合理加括号
知识归纳
二、新知探究
3.利用平方差公式计算:
(1) (5+6x )( 5-6x ) ; (2) (x-2y)(x+2y);(3) (-m+n)(-m-n)
解:(1)原式=52-(6x)2=25-36x2;
(2)原式=x2-(2y)2=x2 - 4y2;
(3)原式=(-m)2-n2=m2-n2.
跟踪练习
二、新知探究
4.利用平方差公式计算:
(1) (2) (ab+8)(ab-8).
(2)原式=(ab)2-82
=a2b2-64.
跟踪练习
解:(1)原式=
;
二、新知探究
想一想:(a-b)(-a-b)=?你是怎样做的?
解:(a-b)(-a-b)
=(-b+a)(-b-a)
=(-b)2-a2
=b2-a2
变形
应用平方差公式
二、新知探究
平方差公式的计算步骤:
(1)找准公式中的相同项a和相反项b,利用加法交换律调整两个二项式的位置,使之与公式左边对应;
(2)用相同项的平方减去相反项的平方.
知识归纳
三、典例精析
解:(1)(-a+b)(-a-b)
=(-a)2-b2
=a2-b2.
例1 利用平方差公式计算:
(1)(-a+b)(-a-b); (2)(0.25x+y)(-0.25x+y).
(2)(0.25x+y)(-0.25x+y)
=(y+0.25x)·(y-0.25x)
=y2-(0.25x)2
=y2-0.0625x2.
三、典例精析
例2:先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2.
解:(2x-y)(y+2x)-(2y+x)(2y-x)
=4x2-y2- (4y2-x2)
=4x2-y2-4y2+x2
=5x2-5y2.
当x=1,y=2时,
原式=5×12-5×22=-15.
3.计算(-4a-1)(4a-1)的结果为 ( )
A.16a2-1 B.-8a2-1 C.-4a2+1 D.-16a2+1
2.下列各式中不能用平方差公式计算的是( )
A.(x-y)(-x+y) B.(-x+y)(-x-y)
C.(-x-y)(x-y) D.(x+y)(-x+y)
四、当堂练习
1.计算(1+2c)(1-2c)的结果是 ( )
A.4c2-1 B.1-4c2 C.4c2-4c+1 D.1+4c+4c2
B
A
D
6.若a2-b2=,a-b=,则a+b= .
5.对于任意的整数n,能整除(n+3)(n-3)-(n+2)(n-2)的整数是( )
A.4 B.3 C.5 D.2
四、当堂练习
4.若(2-x)(2+x)(4+x2)=16-xn,则n的值等于 ( )
A.6 B.4 C.3 D.2
B
C
7.若(x-ay)(x+ay)=x2-16y2,则a= .
8.一个长方体的池塘长为(4a2+9b2)m,宽为(2a+3b)m,高为(2a-3b)m,则这个池塘的容积是 m3.
±4
(16a4-81b4)
四、当堂练习
(2) (-4x2-3y3)(4x2-3y3)=(-3y3)2-(4x2)2=9y6-16x4.
9.计算:(1)()(); (2)(-4x2-3y3)(4x2-3y3).
四、当堂练习
10.计算:(1)a(1-2a)+2(a+1)(a-1); (2)(2x-3y)(3y+2x)-(4y-3x)(3x+4y);
(3)(-am+bn)(am+bn).
解:(1)原式=a-2a2+2(a2-1)=a-2a2+2a2-2=a-2.
(2)原式=4x2-9y2-16y2+9x2=13x2-25y2.
(3)(-am+bn)(am+bn)=(bn)2-(am)2=b2n-a2m.
四、当堂练习
11.先化简,再求值:(3-x)(3+x)+(x+1)2,其中x=2.
解:原式=9-x2+x2+2x+1
=2x+10.
当x=2时,
原式=2×2+10=14.
五、课堂小结
两个数的和与这两个数的差的积,等于这两个数的平方差.
符号表示:(a+b)(a-b)=a2-b2
紧紧抓住 “一同一反”这一特征.不能直接应用公式的,要经过变形才可以应用.
平方差公式
注意
内容
六、作业布置
习题1.9
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
