21.5 二元二次方程和方程组 课件(共32张PPT)-2023-2024学年八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 21.5 二元二次方程和方程组 课件(共32张PPT)-2023-2024学年八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览











文档简介
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 21章代数方程
21.5二元二次方程和方程组
学习目标
1、知道二元二次方程和方程组的概念;知道二元二次方程的一般形式,能识别二次项、一次项和常数项.(重点)
2、了解二元二次方程(组)的解的概念,能判断给出的“一对未知数的取值”是不是已知二元二次方程或方程组的解.(重点)
3、经历二元一次方程(组)的概念和二元二次方程(组)的解的概念的形成过程,发展观察、归纳能力,体会类比的思想方法.
如图,有一个大正方形,是由四个全等的直角三角形与中间的小正方形拼成的,如果大正方形的面积是13,小正方形的面积是1,那么直角三角形的两条直角边分别是多少?
问 题 1
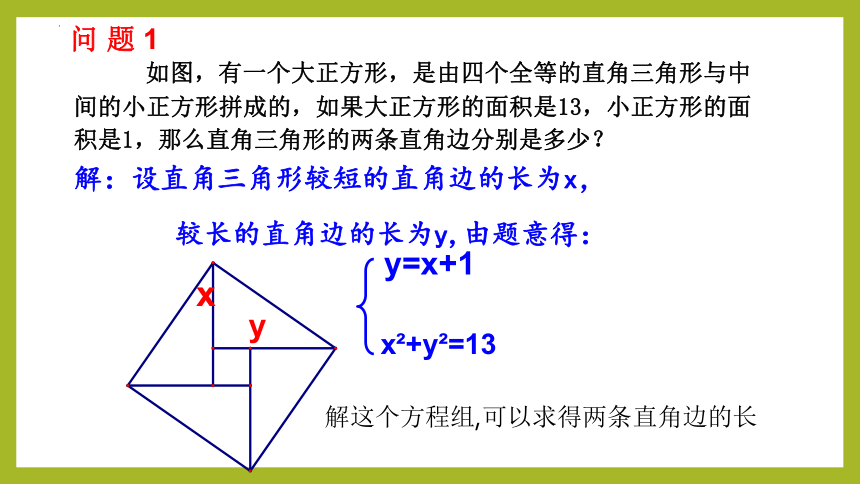
如图,有一个大正方形,是由四个全等的直角三角形与中间的小正方形拼成的,如果大正方形的面积是13,小正方形的面积是1,那么直角三角形的两条直角边分别是多少?
解:设直角三角形较短的直角边的长为x,
较长的直角边的长为y,由题意得:
y=x+1
x?+y?=13
x
y
问 题 1
解这个方程组,可以求得两条直角边的长
问题2
某剧场管理人员为了让观众有更舒适的欣赏环境,对座位进行了调整.已知剧场原有座位 500 个,每排的座位数一样多;现在每排减少了2个座位,并减少了 5排,剧场座位数相应减少为 345个.剧场原有座位的排数是多少? 每排有多少个座位?
设剧场原有座位的排数为 x,每排座位数为 y根据题意可列出方程 xy=500 和方程(x-5)(y一2)=345,即 xy-2x -5y=335;再将它们联立成方程组:
某剧场管理人员为了让观众有更舒适的欣赏环境,对座位进行了调整。已知剧场原有座位500个,每排的座位数一样多;现在每排减少了2个座位,并减少了5排,剧场座位数相应减少为345个。剧场原有座位的排数是多少,原来每排有多少个座位?
解:设剧场原有座位的排数为x,原来每排座位数位为y,由题意得:
xy=500
(x-5)(y-2)=345
xy=500
xy-2x-5y=335
问 题 2
整
理
解这个方程组,可求得剧场原来座位的排数与每排的座位数.
观察
在上面问题 1与问题 2 列出的方程中,方程(2)(3)(4)有什么特点?它们与方程(1)有什么区别?
仅含有两个未知数
含有未知数的项的最高次数是2
整式方程
关于x、y的二元二次方程的一般形式是:
条件:
?a、b、c、d、e、f都是常数,
?a、b、c中至少有一个不为零
?当b=0时,a与d不全为0 c与e不全为0
二元二次方程
二元
二次
方程
二次项
一次项
常数项
其中a、b、c分别叫做二次项系数,d、e分别叫做一次项系数,f叫做这个方程的常数项.
方程中
【练一练】下列方程中,二元二次方程是( ____ )
A.2x2+3x-4=0 B.y2+2x=0
C.y(x2+x)=2 D. ????2+1?????3=0
?
【解析】解:A、方程中含有一个未知数;故本选项错误;
B、方程中含有两个未知数,且未知数的次数是2,符合二元二次方程的定义;故本选项正确;
C、由原方程,得yx2+yx=2,该方程的最高次数是3;故本选项错误;
D、由原方程,得y2x-3y2+1=0该方程的最高次数是3;故本选项错误.
B
故选:B.
再进一步观察,可见问题 1 中得到的方程组是由一个二元一次方程与一个二元二次方程所组成的;问题 2 中得到的方程组是由两个二元二次方程所组成的.
对每个方程组而言,它们有共同特点:
仅含有两个未知数,各方程是整式方程,并且含有未知数的项的最高次数为 2.
像这样的方程组叫做二元二次方程组
【练一练】下列方程组中是二元二次方程组有( )个.
(1) ????2+????=2????+????=4 (2) 2????+????=7????(?????????)=5 (3) ????????+5=?????????????2=???? (4) ????????????=?5????2+????2=5 .
A.1 B.2 C.3 D.4
?
【解析】解:(1) ????????+????=????????+????=???? 次数是2,符合二元二次方程组,
(2) ????????+????=????????(?????????)=????次数是2,符合二元二次方程组,
(3) ????????+????=?????????????????=???? 次数是2,不符合二元二次方程组,
(4) ????????????=?????????????+????????=???? 有三个未知数,不符合二元二次方程组,
故选:B.
?
xy=500
xy-2x-5y=335
y=x+1
x?+y?=13
这两个方程组之间的异同点?
二元二次方程组:仅含有两个未知数,各方程都是整式方程,并且含有未知数的项的最高次数为2,这样的方程组叫做二元二次方程组。
第一类二元二次方程组
第二类二元二次方程组
思 考
操作
表中x、y 的每一组对应值,如:
像这样,能使二元二次方程左右两边的值相等的一对未知数的值,叫做二元二次方程的解.
上面所列的 x、y 的每一组对应值,都是二元二次方程的个解.这个方程还有其他的解.
二元一次方程有无数个实数解;二元二次方程的实数解的个数有多种情况
在方程(1)和方程(2)的解中,如
它们既是方程(1)的解,又是方程(2)的解,即它们是这两个方程的公共解.
方程组中所含各方程的公共解叫做这个方程组的解
对于由方程(1)和方程(2)组成的二元二次方程组,
都是这个方程组的解.
由问题1 中所设x、y 的实际意义,可知 是问题1的解y=3
即直角三角形的一条直角边的长为 2,另一条直角边的长为 3.
例1. 判断下列二元二次方程解的情况:
x2+(y+2)2=4
无数解
(x-2)2+(y-3)2=0
只有一个解
(x-1)2+(y+2)2= -5
无解
与二元一次方程不同,二元二次方程的解可能有无数组解、只有一组解、或无解。
(1)x2+y2-4y=0
(2)x2+y2-4x-6y+13=0
(3)x2+y2-2x+4y+10=0
1.下列方程中,哪些是二元二次方程?
√
课本练习
2.根据二元二次方程组的定义,判断下列方程组中,哪些是二元二次方程组?
√
3.已知下面三对数值:
(1)哪几对数值是方程 的解?
(2)哪几对数值是方程组 的解?
4.试写出一个二元二次方程,使该方程
有一个解是
1.下列方程组中,是二元二次方程组的有( ____ )
① ????+????=1,????????=?2; ② ????2?????2=4,?????????=1; ③ ????2+??2=3,????+????=2; ④ 2????2??????????????2=1,????2+7????2=1.
A.4个 B.3个 C.2个 D.1个
?
【解析】解:①②④是二元二次方程组,③不是二元二次方程组(方程组中第二个方程不是整式方程),
所以二元二次方程组的个数是3,
B
故选:B.
随堂检测
2.下列方程中,是二元二次方程的有( ____ )
①2x-3y=1;②2x2-3y=7;③x2-2xy-3y2=0;④2xy=1.
A.4个 B.3个 C.2个 D.1个
【解析】解:①方程2x-3y=1是二元一次方程,不是二元二次方程,
②方程2x2-3y=7是二元二次方程,
③方程x2-2xy-3y2=0是二元二次方程,
④方程2xy=1是二元二次方程,
B
即二元二次方程有3个,
故选:B.
3.下列方程中,是二元二次方程的为( ____ )
A. ????=1?????1 B.x2+2y=1
C.y=-2x+1 D.y2+2y-7=0
?
【解析】解:y= ???????? -1是二元方程不是二次方程,A选项不符合题意;
x2+2y=1是二元二次方程,B选项符合题意;
y=-2x+1是二元一次方程,C选项不符合题意;
y2+2y-7=0是一元二次方程,D选项不符合题意.
?
B
故选:B.
4.方程组 ????=1,????2=2 ____ 二元二次方程组.(填“是”或“不是”)
?
【解析】解:方程组是二元二次方程组,
故答案为:是.
是
5.已知二元二次方程组有一组解是 ????=?2????=1 ,写出一个符合上述条件的二元二次方程组为 .
?
【解析】解:把x,y的值代入 ????+????=?????????????=????? 符合要求;
故答案为: ????+????=?????????????=????? .
?
6.写出一个二元二次方程,使该方程有一个解是 ????=1????=2 ,那么这个方程可以是 ____________ .
?
【解析】解:答案不唯一,例如:x+xy+y=5,x2+y=3,等等.
故答案为:x+xy+y=5(答案不唯一).
x+xy+y=5
7.写出一个二元二次方程 ,使得该方程有一个解是 ????=2????=?1 .
?
【解析】解:∵22+(-1)2=5,
∴x2+y2=5.
故答案为:x2+y2=5(答案不唯一).
8.写出二元二次方程 x2+y2=13的整数解是 .
【解析】解:∵13=4+9,
∴二元二次方程 x2+y2=13的整数解是 ????=?????????=????? 或 ????=?????????=???? 或 ????=????????=????? 或 ????=????????=???? 或 ????=?????????=????? 或 ????=?????????=???? 或 ????=????????=????? 或 ????=????????=???? .
故答案为: ????=?????????=????? 或 ????=?????????=???? 或 ????=????????=????? 或 ????=????????=???? 或 ????=?????????=????? 或 ????=?????????=???? 或 ????=????????=????? 或 ????=????????=???? .
?
9.下列方程中,哪些是二元二次方程?
(1)x2+y=1;
(2)3-2y2+y=0;
(3) 1???????? +2y2-x=0;
(4)x+y+32=1.
?
【解析】解:(1)x2+y=1是二元二次方程;
(2)3-2y2+y=0是一元二次方程,故不是二元二次方程;
(3) ???????????? +2y2-x=0等号左边不是整式,故不是二元二次方程;
(4)x+y+32=1是二元一次方程,故不是二元二次方程.
?
10.请你构造一个二元二次方程组,使它的 ????1=2,????1=3; ????2=3,????2=?2.
?
【解析】解:∵二元二次方程组的解为 ????????=????????????=???? , ????????=????????????=????? ,
∴二元二次方程组可以为 ????????+????????=????????????????=???? ,
故答案为: ????????+????????=????????????????=???? .(答案不唯一)
?
11.下列方程组中,哪些是二元二次方程组?
(1) 3????=2????2+?????????????=2 ;(2) ????????+????=20????????+????=18 ;
(3) ????+5=????3?????????=?1 ; (4) 3????2=?????1????+3????=5 .
?
【解析】解:(1) ????????=????????????+?????????????=???? 是二元二次方程组;
(2) ????????+????=????????????????+????=???????? 是二元二次方程组;
(3) ????+????=?????????????????=????? 是二元一次方程组;
(4) ????????????=?????????????+????????=???? 是无理方程组.
?
1、二元二次方程(组).
2、二元二次方程的解和二元二次方程组的解.
课堂小结
第 21章代数方程
21.5二元二次方程和方程组
学习目标
1、知道二元二次方程和方程组的概念;知道二元二次方程的一般形式,能识别二次项、一次项和常数项.(重点)
2、了解二元二次方程(组)的解的概念,能判断给出的“一对未知数的取值”是不是已知二元二次方程或方程组的解.(重点)
3、经历二元一次方程(组)的概念和二元二次方程(组)的解的概念的形成过程,发展观察、归纳能力,体会类比的思想方法.
如图,有一个大正方形,是由四个全等的直角三角形与中间的小正方形拼成的,如果大正方形的面积是13,小正方形的面积是1,那么直角三角形的两条直角边分别是多少?
问 题 1
如图,有一个大正方形,是由四个全等的直角三角形与中间的小正方形拼成的,如果大正方形的面积是13,小正方形的面积是1,那么直角三角形的两条直角边分别是多少?
解:设直角三角形较短的直角边的长为x,
较长的直角边的长为y,由题意得:
y=x+1
x?+y?=13
x
y
问 题 1
解这个方程组,可以求得两条直角边的长
问题2
某剧场管理人员为了让观众有更舒适的欣赏环境,对座位进行了调整.已知剧场原有座位 500 个,每排的座位数一样多;现在每排减少了2个座位,并减少了 5排,剧场座位数相应减少为 345个.剧场原有座位的排数是多少? 每排有多少个座位?
设剧场原有座位的排数为 x,每排座位数为 y根据题意可列出方程 xy=500 和方程(x-5)(y一2)=345,即 xy-2x -5y=335;再将它们联立成方程组:
某剧场管理人员为了让观众有更舒适的欣赏环境,对座位进行了调整。已知剧场原有座位500个,每排的座位数一样多;现在每排减少了2个座位,并减少了5排,剧场座位数相应减少为345个。剧场原有座位的排数是多少,原来每排有多少个座位?
解:设剧场原有座位的排数为x,原来每排座位数位为y,由题意得:
xy=500
(x-5)(y-2)=345
xy=500
xy-2x-5y=335
问 题 2
整
理
解这个方程组,可求得剧场原来座位的排数与每排的座位数.
观察
在上面问题 1与问题 2 列出的方程中,方程(2)(3)(4)有什么特点?它们与方程(1)有什么区别?
仅含有两个未知数
含有未知数的项的最高次数是2
整式方程
关于x、y的二元二次方程的一般形式是:
条件:
?a、b、c、d、e、f都是常数,
?a、b、c中至少有一个不为零
?当b=0时,a与d不全为0 c与e不全为0
二元二次方程
二元
二次
方程
二次项
一次项
常数项
其中a、b、c分别叫做二次项系数,d、e分别叫做一次项系数,f叫做这个方程的常数项.
方程中
【练一练】下列方程中,二元二次方程是( ____ )
A.2x2+3x-4=0 B.y2+2x=0
C.y(x2+x)=2 D. ????2+1?????3=0
?
【解析】解:A、方程中含有一个未知数;故本选项错误;
B、方程中含有两个未知数,且未知数的次数是2,符合二元二次方程的定义;故本选项正确;
C、由原方程,得yx2+yx=2,该方程的最高次数是3;故本选项错误;
D、由原方程,得y2x-3y2+1=0该方程的最高次数是3;故本选项错误.
B
故选:B.
再进一步观察,可见问题 1 中得到的方程组是由一个二元一次方程与一个二元二次方程所组成的;问题 2 中得到的方程组是由两个二元二次方程所组成的.
对每个方程组而言,它们有共同特点:
仅含有两个未知数,各方程是整式方程,并且含有未知数的项的最高次数为 2.
像这样的方程组叫做二元二次方程组
【练一练】下列方程组中是二元二次方程组有( )个.
(1) ????2+????=2????+????=4 (2) 2????+????=7????(?????????)=5 (3) ????????+5=?????????????2=???? (4) ????????????=?5????2+????2=5 .
A.1 B.2 C.3 D.4
?
【解析】解:(1) ????????+????=????????+????=???? 次数是2,符合二元二次方程组,
(2) ????????+????=????????(?????????)=????次数是2,符合二元二次方程组,
(3) ????????+????=?????????????????=???? 次数是2,不符合二元二次方程组,
(4) ????????????=?????????????+????????=???? 有三个未知数,不符合二元二次方程组,
故选:B.
?
xy=500
xy-2x-5y=335
y=x+1
x?+y?=13
这两个方程组之间的异同点?
二元二次方程组:仅含有两个未知数,各方程都是整式方程,并且含有未知数的项的最高次数为2,这样的方程组叫做二元二次方程组。
第一类二元二次方程组
第二类二元二次方程组
思 考
操作
表中x、y 的每一组对应值,如:
像这样,能使二元二次方程左右两边的值相等的一对未知数的值,叫做二元二次方程的解.
上面所列的 x、y 的每一组对应值,都是二元二次方程的个解.这个方程还有其他的解.
二元一次方程有无数个实数解;二元二次方程的实数解的个数有多种情况
在方程(1)和方程(2)的解中,如
它们既是方程(1)的解,又是方程(2)的解,即它们是这两个方程的公共解.
方程组中所含各方程的公共解叫做这个方程组的解
对于由方程(1)和方程(2)组成的二元二次方程组,
都是这个方程组的解.
由问题1 中所设x、y 的实际意义,可知 是问题1的解y=3
即直角三角形的一条直角边的长为 2,另一条直角边的长为 3.
例1. 判断下列二元二次方程解的情况:
x2+(y+2)2=4
无数解
(x-2)2+(y-3)2=0
只有一个解
(x-1)2+(y+2)2= -5
无解
与二元一次方程不同,二元二次方程的解可能有无数组解、只有一组解、或无解。
(1)x2+y2-4y=0
(2)x2+y2-4x-6y+13=0
(3)x2+y2-2x+4y+10=0
1.下列方程中,哪些是二元二次方程?
√
课本练习
2.根据二元二次方程组的定义,判断下列方程组中,哪些是二元二次方程组?
√
3.已知下面三对数值:
(1)哪几对数值是方程 的解?
(2)哪几对数值是方程组 的解?
4.试写出一个二元二次方程,使该方程
有一个解是
1.下列方程组中,是二元二次方程组的有( ____ )
① ????+????=1,????????=?2; ② ????2?????2=4,?????????=1; ③ ????2+??2=3,????+????=2; ④ 2????2??????????????2=1,????2+7????2=1.
A.4个 B.3个 C.2个 D.1个
?
【解析】解:①②④是二元二次方程组,③不是二元二次方程组(方程组中第二个方程不是整式方程),
所以二元二次方程组的个数是3,
B
故选:B.
随堂检测
2.下列方程中,是二元二次方程的有( ____ )
①2x-3y=1;②2x2-3y=7;③x2-2xy-3y2=0;④2xy=1.
A.4个 B.3个 C.2个 D.1个
【解析】解:①方程2x-3y=1是二元一次方程,不是二元二次方程,
②方程2x2-3y=7是二元二次方程,
③方程x2-2xy-3y2=0是二元二次方程,
④方程2xy=1是二元二次方程,
B
即二元二次方程有3个,
故选:B.
3.下列方程中,是二元二次方程的为( ____ )
A. ????=1?????1 B.x2+2y=1
C.y=-2x+1 D.y2+2y-7=0
?
【解析】解:y= ???????? -1是二元方程不是二次方程,A选项不符合题意;
x2+2y=1是二元二次方程,B选项符合题意;
y=-2x+1是二元一次方程,C选项不符合题意;
y2+2y-7=0是一元二次方程,D选项不符合题意.
?
B
故选:B.
4.方程组 ????=1,????2=2 ____ 二元二次方程组.(填“是”或“不是”)
?
【解析】解:方程组是二元二次方程组,
故答案为:是.
是
5.已知二元二次方程组有一组解是 ????=?2????=1 ,写出一个符合上述条件的二元二次方程组为 .
?
【解析】解:把x,y的值代入 ????+????=?????????????=????? 符合要求;
故答案为: ????+????=?????????????=????? .
?
6.写出一个二元二次方程,使该方程有一个解是 ????=1????=2 ,那么这个方程可以是 ____________ .
?
【解析】解:答案不唯一,例如:x+xy+y=5,x2+y=3,等等.
故答案为:x+xy+y=5(答案不唯一).
x+xy+y=5
7.写出一个二元二次方程 ,使得该方程有一个解是 ????=2????=?1 .
?
【解析】解:∵22+(-1)2=5,
∴x2+y2=5.
故答案为:x2+y2=5(答案不唯一).
8.写出二元二次方程 x2+y2=13的整数解是 .
【解析】解:∵13=4+9,
∴二元二次方程 x2+y2=13的整数解是 ????=?????????=????? 或 ????=?????????=???? 或 ????=????????=????? 或 ????=????????=???? 或 ????=?????????=????? 或 ????=?????????=???? 或 ????=????????=????? 或 ????=????????=???? .
故答案为: ????=?????????=????? 或 ????=?????????=???? 或 ????=????????=????? 或 ????=????????=???? 或 ????=?????????=????? 或 ????=?????????=???? 或 ????=????????=????? 或 ????=????????=???? .
?
9.下列方程中,哪些是二元二次方程?
(1)x2+y=1;
(2)3-2y2+y=0;
(3) 1???????? +2y2-x=0;
(4)x+y+32=1.
?
【解析】解:(1)x2+y=1是二元二次方程;
(2)3-2y2+y=0是一元二次方程,故不是二元二次方程;
(3) ???????????? +2y2-x=0等号左边不是整式,故不是二元二次方程;
(4)x+y+32=1是二元一次方程,故不是二元二次方程.
?
10.请你构造一个二元二次方程组,使它的 ????1=2,????1=3; ????2=3,????2=?2.
?
【解析】解:∵二元二次方程组的解为 ????????=????????????=???? , ????????=????????????=????? ,
∴二元二次方程组可以为 ????????+????????=????????????????=???? ,
故答案为: ????????+????????=????????????????=???? .(答案不唯一)
?
11.下列方程组中,哪些是二元二次方程组?
(1) 3????=2????2+?????????????=2 ;(2) ????????+????=20????????+????=18 ;
(3) ????+5=????3?????????=?1 ; (4) 3????2=?????1????+3????=5 .
?
【解析】解:(1) ????????=????????????+?????????????=???? 是二元二次方程组;
(2) ????????+????=????????????????+????=???????? 是二元二次方程组;
(3) ????+????=?????????????????=????? 是二元一次方程组;
(4) ????????????=?????????????+????????=???? 是无理方程组.
?
1、二元二次方程(组).
2、二元二次方程的解和二元二次方程组的解.
课堂小结
