12.6 实数的运算( 第1课时) 课件(共22张PPT)-2023-2024学年七年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 12.6 实数的运算( 第1课时) 课件(共22张PPT)-2023-2024学年七年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
12.6 实数的运算
第1课时
2023-2024学年沪教版七年级下册数学课件
实数的加、减、乘、除、乘方等运算的意义,与有理数运算的意义一样.
实数都可以表示为小数(包括整数)的形式,其中无理数是无限不循环小数。在实数运算中,对于涉及无限小数的运算,可以根据保留几位小数的要求,取无限小数的近似值(有限小数)进行运算,逐步接近原来运算的结果.这样,实数的运算就转化为有限小数的运算.
我们学过的有理数的运算法则、运算性质以及运算顺序的规定,在实数范围内仍旧适用,开方与乘方是同级运算.
对于涉及无理数的实数运算,如果没有指明运算结果保留几位小数,那么通常是利用实数的运算法则和运算性质对算式进行化简,其结果可能是化简了的一个算式,如:
例题1 不用计算器,计算:
合并同类项
解:原式
(乘法对于加法的分配律)
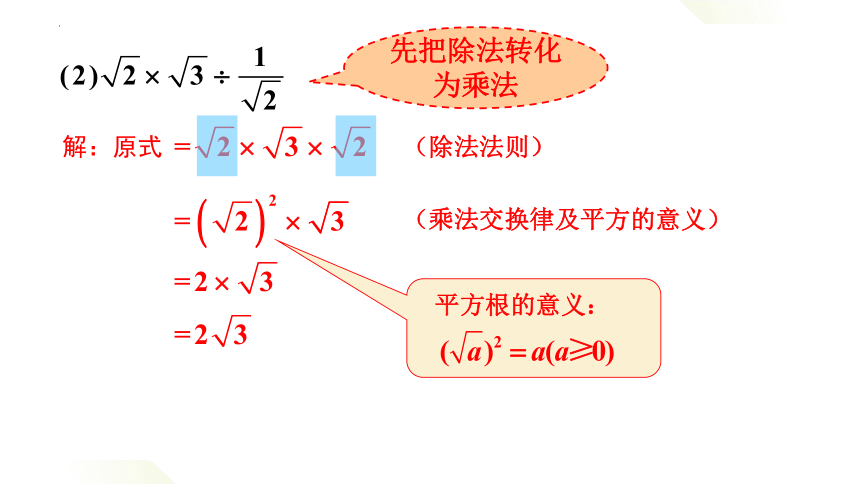
解:原式
先把除法转化
为乘法
(除法法则)
(乘法交换律及平方的意义)
平方根的意义:
实数的乘方
平方根的意义:
解:原式
(乘方的意义)
(乘方的意义)
解:原式=
(平方根的意义及除法法则)
(乘法对于加法的分配律)
变式1 计算下列各式的值:
例题2 用计算器计算,直接写出计算器显示的结果:
设a>0,b>0,可知
根据平方根的意义,得
同理
、
例题3 不用计算器,计算:
解:原式
先乘方
再求和
最后求算术平方根
解:原式
利用同底数幂除法法则
解:原式
先合并小括号里的
乘法分配律
解:原式=
1.下列运算正确的是( C )
C
A.=a B.-=
C.2+5=7 D.-(a-b)=-a-b
2.比较实数0,-,2,-的大小,其中最小的实数为
( B )
B
A.0 B.-
C.2 D.-
3.大于-的所有负整数是 -3,-2,-1 .
解:3<<4,∴-4<-<-3,
∴大于-的所有负整数是-3,-2,-1.
4.设a=,b=,c=3,则a,b,c的大小关系为
a<c<b .
a<c<b
解:∵<<,∴2<<3,即2<a<3.
∵<<,∴3<<4,∴3<b<4.
∵c=3,∴a<c<b.
-3,-2,-1
5.李明同学设计了如图所示的一个实数运算流程图,当输入x的值为时,输出的数值为 .
点拨:根据题中流程图,得算式为(x2-2)÷7,当x=
时,(x2-2)÷7=[()2-2]÷7=.故答案为.
6.计算:
(1)+-5;
解:(1)原式=-7-5×0.8=-.
(2)(-2)3×-×;
解:(2)原式=-8×-3×
=-1+1=0.
(3)+++1.
解:(3)++|-|+1
=-3+×4++1
=-3+2++1
=.
7.(1)化简(结果保留根号):
①|1-|= -1 ;
②|-|= - ;
③|-|= - ;
④|-|= - .
-1
-
-
-
(2)计算(结果保留根号):
|-|+|-|+|-|+…+|-|.
解:原式=(-)+(-)+(-)+…+(-)=-.
8.阅读下列材料:规定实数m的整数部分记为[m],小数部
分记为{m}.例如:[]=2,{}=-2.
解答下列问题:
(1)[]= 4 ,{}= -5 ;
4
-5
(2)求{}+{13-}的值.
解:∵3<<4,
∴{}=-3,-4<-<-3,
∴9<13-<10,
∴{13-}=13--9=4-,
∴原式=(-3)+(4-)=1.
谢谢
12.6 实数的运算
第1课时
2023-2024学年沪教版七年级下册数学课件
实数的加、减、乘、除、乘方等运算的意义,与有理数运算的意义一样.
实数都可以表示为小数(包括整数)的形式,其中无理数是无限不循环小数。在实数运算中,对于涉及无限小数的运算,可以根据保留几位小数的要求,取无限小数的近似值(有限小数)进行运算,逐步接近原来运算的结果.这样,实数的运算就转化为有限小数的运算.
我们学过的有理数的运算法则、运算性质以及运算顺序的规定,在实数范围内仍旧适用,开方与乘方是同级运算.
对于涉及无理数的实数运算,如果没有指明运算结果保留几位小数,那么通常是利用实数的运算法则和运算性质对算式进行化简,其结果可能是化简了的一个算式,如:
例题1 不用计算器,计算:
合并同类项
解:原式
(乘法对于加法的分配律)
解:原式
先把除法转化
为乘法
(除法法则)
(乘法交换律及平方的意义)
平方根的意义:
实数的乘方
平方根的意义:
解:原式
(乘方的意义)
(乘方的意义)
解:原式=
(平方根的意义及除法法则)
(乘法对于加法的分配律)
变式1 计算下列各式的值:
例题2 用计算器计算,直接写出计算器显示的结果:
设a>0,b>0,可知
根据平方根的意义,得
同理
、
例题3 不用计算器,计算:
解:原式
先乘方
再求和
最后求算术平方根
解:原式
利用同底数幂除法法则
解:原式
先合并小括号里的
乘法分配律
解:原式=
1.下列运算正确的是( C )
C
A.=a B.-=
C.2+5=7 D.-(a-b)=-a-b
2.比较实数0,-,2,-的大小,其中最小的实数为
( B )
B
A.0 B.-
C.2 D.-
3.大于-的所有负整数是 -3,-2,-1 .
解:3<<4,∴-4<-<-3,
∴大于-的所有负整数是-3,-2,-1.
4.设a=,b=,c=3,则a,b,c的大小关系为
a<c<b .
a<c<b
解:∵<<,∴2<<3,即2<a<3.
∵<<,∴3<<4,∴3<b<4.
∵c=3,∴a<c<b.
-3,-2,-1
5.李明同学设计了如图所示的一个实数运算流程图,当输入x的值为时,输出的数值为 .
点拨:根据题中流程图,得算式为(x2-2)÷7,当x=
时,(x2-2)÷7=[()2-2]÷7=.故答案为.
6.计算:
(1)+-5;
解:(1)原式=-7-5×0.8=-.
(2)(-2)3×-×;
解:(2)原式=-8×-3×
=-1+1=0.
(3)+++1.
解:(3)++|-|+1
=-3+×4++1
=-3+2++1
=.
7.(1)化简(结果保留根号):
①|1-|= -1 ;
②|-|= - ;
③|-|= - ;
④|-|= - .
-1
-
-
-
(2)计算(结果保留根号):
|-|+|-|+|-|+…+|-|.
解:原式=(-)+(-)+(-)+…+(-)=-.
8.阅读下列材料:规定实数m的整数部分记为[m],小数部
分记为{m}.例如:[]=2,{}=-2.
解答下列问题:
(1)[]= 4 ,{}= -5 ;
4
-5
(2)求{}+{13-}的值.
解:∵3<<4,
∴{}=-3,-4<-<-3,
∴9<13-<10,
∴{13-}=13--9=4-,
∴原式=(-3)+(4-)=1.
谢谢
