第 20章 一次函数单元复习 课件(共67张PPT)-2023-2024学年八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 第 20章 一次函数单元复习 课件(共67张PPT)-2023-2024学年八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 00:00:00 | ||
图片预览










文档简介
单元复习课件
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 20章 一次函数
一.一次函数的定义
二.一次函数的图象
三.一次函数的性质
四.一次函数图象与系数的关系
五.一次函数图象上点的坐标特征
六.一次函数图象与几何变换
七.待定系数法求一次函数解析式
八.一次函数与一元一次方程
九.一次函数与一元一次不等式
一十.一次函数与二元一次方程
一十一根据实际问题列一次函数关系式
一十二一次函数的应用
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
当k=0时,函数y=b(b是常数)叫做______函数。
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
1
k≠0
2、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
b
一条直线
常值
要点回顾
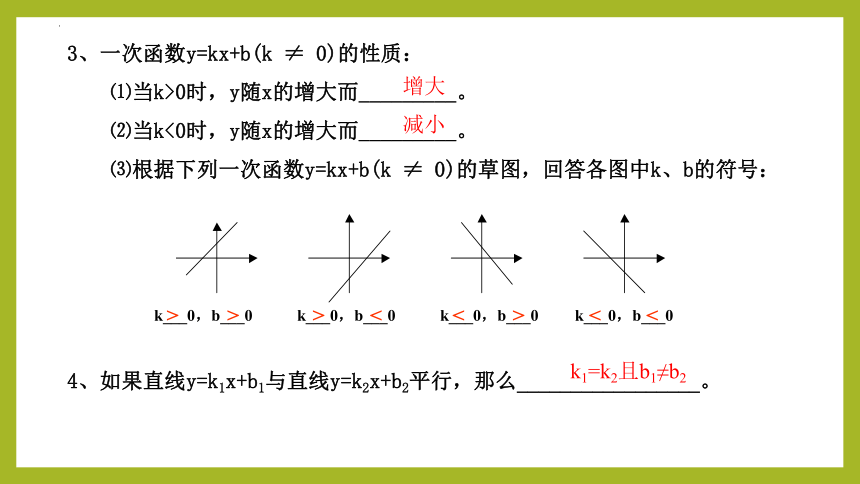
3、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图,回答各图中k、b的符号:
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
增大
减小
4、如果直线y=k1x+b1与直线y=k2x+b2平行,那么_________________。
k1=k2且b1≠b2
1.下列函数中,是一次函数的是( ____ )
A.y= 12???? +1 B.y=2x+1
C.y=x2+1 D.y=kx+b(k、b是常数)
?
【解析】解:A选项的分母中有未知数,不是整式,故该选项不符合题意;
B选项符合y=kx+b(k≠0)的形式,故该选项符合题意;
C选项是二次函数,故该选项不符合题意;
D选项没有强调k≠0,故该选项不符合题意;
B
一.一次函数的定义
故选:B.
2.下列函数中,y是x的一次函数的是( ____ )
A.y=x2-5 B.y=3
C.y=kx+b D.y=x-1
【解析】解:A、自变量x的次数是2,不是一次函数,故此选项不符合题意;
B、没有自变量,不是一次函数,故此选项不符合题意;
C、自变量x的系数k可能为0,故此选项不符合题意;
D、是一次函数,故此选项符合题意;
D
故选:D.
3.在直角坐标平面内,一次函数y=ax+b的图象如图所示,那么下列说法正确的是( ____ )
A.当x>0时,y>-2 B.当x<1时,y>0
C.当x<0时,-2<y<0 D.当x≥1时,y≤0
【解析】解:由函数y= ???????? x+3的图象可知,
当x>0时,y>-2,故A正确;
当x<1时,y<0,B选项错误;
当x<0时,y<-2,C选项错误;
?
A
二.一次函数的图象
当x≥1时,y≥0,故D错误.
故选:A.
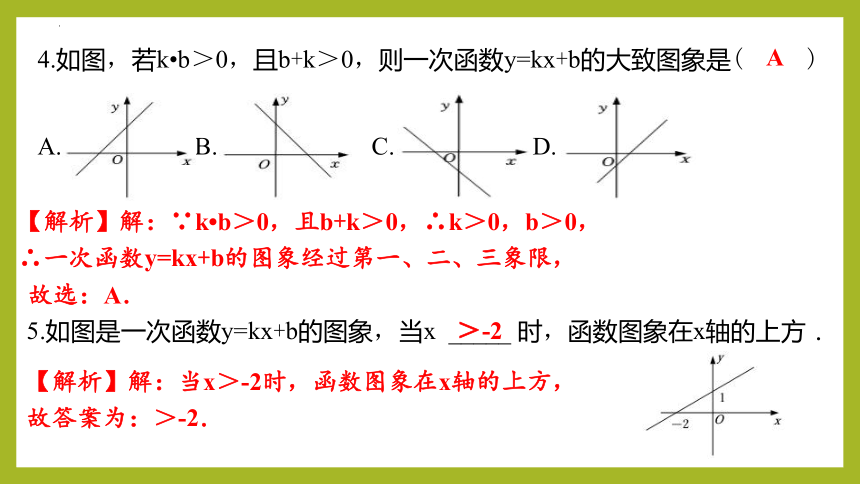
4.如图,若k?b>0,且b+k>0,则一次函数y=kx+b的大致图象是( ____ )
A.___B.___ C. D.
A
【解析】解:∵k?b>0,且b+k>0,∴k>0,b>0,
∴一次函数y=kx+b的图象经过第一、二、三象限,
故选:A.
5.如图是一次函数y=kx+b的图象,当x _____ 时,函数图象在x轴的上方.
>-2
【解析】解:当x>-2时,函数图象在x轴的上方,
故答案为:>-2.
6.如果ab<0,ac<0,则直线 ????=?????????????????????? 不经过( ____ )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
?
【解析】解:∵ab<0,ac<0,
∴a,b异号,a,c异号,
∴ ?????????>???? ,且b,c同号,
∴ ?????????<???? ,
?
B
三.一次函数的性质
一次函数 ????=?????????????????????? 的图象经过第一、三、四象限,不经过第二象限.故选:B.
?
7.一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是 _____ .
【解析】解:由图象可得,
当y>0时,x的取值范围是x<2,
故答案为:x<2.
x<2
8.已知点A(x1,y1)、B(x2,y2)都在直线y=-x+3上,如果x1<x2,那么y1 ____ y2(填“>”“<”或“=”).
【解析】解:∵k=-1<0,
∴y随x的增大而减小,
又∵点A(x1,y1)、B(x2,y2)都在直线y=-x+3上,且x1<x2,
∴y1>y2.
故答案为:>.
>
9.一次函数 ????=12?????1 的图象不经过的象限是( ____ )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
?
【解析】解:∵y= ???????? x-1,
∴k= ???????? >0,图象经过第一、三象限,
b=-1<0,直线与y轴负半轴相交,图象经过第四象限,
?
B
四.一次函数图象与系数的关系
即一次函数y= ???????? x-1的图象经过第一、三、四象限,不经过第二象限.
故选:B.
?
10.直线y=( 12 k-1)x+2(1-k)的图象经过第一、二、四象限,那么k的取值范围是( ____ )
A.k>2 B.k<2 C.k>1 D.k<1
?
【解析】解:∵直线y=( ???????? k-1)x+2(1-k)的图象经过第一、二、四象限,
?
D
∴ ?????????????????<????????(?????????)>???? ,
解得k<1.
故选:D.
?
11.若一次函数y=kx+b的函数值y随x的增大而减小,且图象与y轴的负半轴相交,那么对k和b的符号判断正确的是( ____ )
A.k>0,b>0
B.k>0,b<0
C.k<0,b>0
D.k<0,b<0
【解析】解:∵一次函数y=kx+b的函数值y随x的增大而减小,∴k<0;
∵图象与y轴的负半轴相交,∴b<0.
故选:D.
D
12.如果一次函数y=(m-3)x-1的函数值y随着x的值增大而减小,那么m取值范围是 _____ .
【解析】解:∵一次函数y=(m-3)x-1的函数值y随着x的值增大而减小,
∴m-3<0,
∴m<3;
故答案为:m<3.
m<3
13.如果直线y=(2m+1)x-2+m经过第一、三、四象限,那么则m的取值范围是 .
【解析】解:∵直线y=(2m+1)x-2+m经过第一、三、四象限,
∴ ????????+????>?????????+????<???? ,
解得:- ???????? <m<2,
∴m的取值范围为- ???????? <m<2.
故答案为:- ???????? <m<2.
?
14.直线y=-x+6与x轴的交点是 ________ .
【解析】解:当y=0时,-x+6=0,
解得:x=6,
∴直线y=-x+6与x轴的交点是(6,0).
故答案为:(6,0).
(6,0)
五.一次函数图象上点的坐标特征
15.已知直线y=kx-3与两坐标轴所围成的三角形的面积为6,
则k的值为 .
【解析】解:依照题意,画出图象,如图所示.
当x=0时,y=kx-3=-3,∴点B的坐标为(0,-3);
当y=0时,kx-3=0,解得:x= ???????? ,
∴点A的坐标为( ???????? ,0).
?
∴S△AOB= ???????? ×3×| ???????? |=6,
解得:k=± ???????? .
故答案为:± ???????? .
?
16.已知一次函数y=kx+1的图象经过点A(2,5),那么k= ____ .
【解析】解:∵一次函数y=kx+1的图象经过点(2,5),
∴5=2k+1,
解得k=2.
故答案为:2.
2
17.在平面直角坐标系xOy中,对于P、Q两点给出如下定义:如果点P到x、y轴的距离中的最小值等于点Q到x、y轴的距离中的最小值,那么称P、Q两点为“坐标轴等距点”,例如点P(2,2)与点Q(-2,-3)为“坐标轴等距点”.已知点A的坐标为(-3,2),如果点B在直线y=x-1上,且A、B两点为“坐标轴等距点”,那么点B的坐标为 _____________________ .
【解析】解:∵点A的坐标为(-3,2),
∴点A到x、y轴的距离中的最小值为2,
∵A、B两点为“坐标轴等距点”,
∴点B到x、y轴的距离中的最小值为2.
当x=-2时,y=-2-1=-3,|-3|>|-2|,
(-2,-3)或(3,2)
∴点B到x、y轴的距离中的最小值为2,
∴点B的坐标为(-2,-3);
当x=2时,y=2-1=1,|1|<|2|,
∴点B到x、y轴的距离中的最小值为1,不符合题意,舍去;
当y=-2时,x-1=-2,
解得:x=-1,
∵|-1|<|-2|,
∴点B到x、y轴的距离中的最小值为1,不符合题意,舍去;
当y=2时,x-1=2,
解得:x=3,
∵|3|>|2|,
∴点B到x、y轴的距离中的最小值为2,
∴点B的坐标为(3,2).
综上所述,点B的坐标为(-2,-3)或(3,2).
故答案为:(-2,-3)或(3,2).
18.如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=- 12 x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 .
?
【解析】解:①当∠ABD=90°时,如图1,则∠DBC+∠ABO=90°,
∴∠DBC=∠BAO,
由直线y=- ???????? x+b交线段OC于点B,交x轴于点A可知OB=b,OA=2b,
?
∵点C(0,4),
∴OC=4,
∴BC=4-b,
在△DBC和△BAO中,
∠????????????=∠????????????∠????????????=∠????????????????????=????????
∴△DBC≌△BAO(AAS),
∴BC=OA,
即4-b=2b,
?
∴b= ???????? ;
②当∠ADB=90°时,如图2,
作AF⊥CE于F,
同理证得△BDC≌△DAF,
∴CD=AF=4,BC=DF,
∵OB=b,OA=2b,
∴BC=DF=2b-4,
∵BC=4-b,
∴2b-4=4-b,
∴b= ???????? ;
?
③当∠DAB=90°时,如图3,
作DF⊥OA于F,
同理证得△AOB≌△DFA,
∴OA=DF,
∴2b=4,
∴b=2;
综上,b的值为 ???????? 或 ???????? 或2.
故答案为 ???????? 或 ???????? 或2.
?
19.把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,已知点A(1,0),B(4,0),现将Rt△ABC沿着x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( ____ )
A.4
B.8
C.16
D.8 2
?
【解析】解:如图所示.
C
___
∵点A、B的坐标分别为(1,0)、(4,0),
∴AB=3.
∵∠CAB=90°,BC=5,
∴AC=4.
∴A′C′=4.
∵点C′在直线y=2x-6上,
∴2x-6=4,解得 x=5.
即OA′=5.
∴CC′=5-1=4.
∴S?BCC′B′=4×4=16.
即线段BC扫过的面积为16.
故选:C.
20.已知:直线 ????=?12????+32 与x轴交于点M,与y轴交于点N,将△MON绕着坐标原点逆时针旋转90°,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.
?
【解析】解:(1)对于直线 ????=?????????????+???????? ,
令y=0得 ????=?????????????+???????? ,解得x=3,
令x=0,得 ????=???????? ,
?
∴直线 ????=?????????????+???????? 与x轴交于点M,与y轴交于点N,
∴OM=3,ON= ???????? ,
∵将△MON绕着坐标原点逆时针旋转90°,与x轴交于点A,与y轴交于点B,
∴OA=ON= ???????? ,OB=OM=3,
∴ ????(?????????,????) ,B(0,3);
?
____
(2)∵OA= ???????? ,OP=2OA,
∴OP=3,
∵过B点作直线BP与x轴交于点P,
∴P(-3,0)或P(3,0),
∵OB=3,
?
∴当P(-3,0)时, ????△????????????=????????×????????×????????=????????×|?????????????|×????=???????? ;
当P(3,0)时, ????△????????????=????????×????????×????????=????????×|????+????????|×????=???????????? .
____
?
21.把直线y=-2x+4向左平移3个单位后,在y轴上的截距为 ____ .
【解析】解:由“左加右减”的原则可知,把直线y=-2x+4向左平移3个单位后所得直线的解析式为y=-2(x+3)+4,即y=-2x-2,
∵把直线y=-2x+4向左平移3个单位后,在y轴上的截距为-2,
故答案为:-2.
-2
六.一次函数图象与几何变换
22.如果把直线y=3x-1沿y轴向下平移3个单位,所得直线的解析式是 _________ .
【解析】解:把直线y=3x-1沿y轴向下平移3个单位,所得直线的解析式是y=3x-4;
故答案为:y=3x-4.
y=3x-4
23.将直线y=2x+1平移,使平移后的直线经过点(0,-3),所得直线的表达式是 _________ .
【解析】解:设平移后的函数表达式是y=2x+b,
∵它经过点(0,-3),
∴-3=b,
解得:b=-3.
∴平移后的函数解析式为:y=2x-3.
故答案为:y=2x-3.
y=2x-3
24.已知一次函数y=kx+b(k≠0)的图象经过点(2,0)与(0,4),那么y随着x的增大而 _____ .(填“增大”或“减小”)
【解析】解:(方法一)将(2,0),(0,4)代入y=kx+b得: ????????+????=????????=???? ,解得: ????=?????????=???? ,
∵k=-2<0,∴y随x的增大而减小.
故答案为:减小.
(方法二)依照题意画出函数图象,如图所示.
?
减小
七.待定系数法求一次函数解析式
观察函数图象,可知:y随x的增大而减小.
故答案为:减小.
25.已知y+2与3x成正比例,当x=1时,y的值为4.
(1)求y与x之间的函数表达式;
(2)求该函数图象与坐标轴围成的三角形周长.
【解析】解:(1)∵y+2与3x成正比例,
∴设y+2=k?3x,
∵当x=1时,y的值为4,
∴4+2=3k,
∴k=2,
∴y+2=6x,
∴y与x之间的函数表达式是y=6x-2,
(2)如图,直线y=6x-2与x、y轴分别交于A、B两点,
当x=0时,y=-2,当y=0时,x= ???????? ,
∴A的坐标是( ???????? ,0),B的坐标是(0,-2),
∴AO= ???????? ,OB=2,
∴AB= ????????????+???????????? = ????????+(????????)???? = ???????????? ,
∴函数图象与坐标轴围成的三角形周长是OA+OB+AB= ???????? +2+ ???????????? = ????+????????????
?
26.已知函数y=f(x)满足当a1≤x≤b1时,对应的函数值y的范围是a1≤y≤b1,我们称该函数为关于a1和b1的方块函数.如果一次函数y=kx+b(k、b为常数,k≠0)是关于1和2的方块函数,且它的图象不经过原点,那么该一次函数的解析式为 _________ .
【解析】解:当x=1时,y=k+b;当x=2时,y=2k+b,
①当 ????+????=????????????+????=???? 时,解得 ????=????????=???? ,∴y=x,不合题意,舍去;
②当 ????+????=????????????+????=???? 时,解得 ????=?????????=???? ,∴y=-x+3;
?
y=-x+3
∴一次函数的解析式为y=-x+3,故答案为:y=-x+3.
27.如图,在直角坐标平面内,△ABC的顶点A(-1,0),点B与点A关于原点对称,AB=BC,∠CAB=30°,将△ABC绕点C旋转,使点A落在x轴上的点D处,点B落在点E处,那么BE所在直线的解析式为 .
【解析】解:如图,过点C作CF⊥x轴于点F,
∵△ABC的顶点A(-1,0),点B与点A关于原点对称,
∴B(1,0),
∴AB=2.
∵AB=BC,∠CAB=30°,
∴BC=AB=2,
∴CF=BC?sin60°=2× ???????? = ???? ,BF=BC?cos30°=2× ???????? =1,
∴C(2, ???? ).
∵将△ABC绕点C旋转,使点A落在x轴上的点D处,点B落在点E处,
∴AB=CE=2,
∴E(4, ???? ).
设直线BE的解析式为y=kx+b(k≠0),
?
∴ ????+????=????????????+????=???? ,解得 ????=????????????=????????? ,
∴BE所在直线的解析式为:y= ???????? x- ???????? .
故答案为:y= ???????? x- ???????? .
?
28.一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为 ______ .
【解析】解:从图象上可知则关于x的方程kx+b=0的解为的解是x=-2.
故答案为:x=-2
x=-2
八.一次函数与一元一次方程
29.直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为 ______ .
【解析】解:两个条直线的交点坐标为(-1,3),且当x>-1时,直线l1在直线l2的上方,故不等式k2x>k1x+b的解集为x<-1.
故本题答案为:x<-1.
x<-1
九.一次函数与一元一次不等式
30.如图,直线y=kx+b经过点(-2,0)和(0,1),那么关于x的不等式kx+b>0的解集为 ______ .
【解析】解:根据函数图象可知,
∴关于x的不等式kx+b>0的解集为x>-2.
故答案为:x>-2.
x>-2
31.已知函数y=x+a与y=-2x+b的交点坐标为(-2,1),则方程组 ?????????=?????2????+????=???? 的解为 .
?
【解析】解:方程组 ?????????=?????????????+????=???? 可变为: ????=????+????????=?????????+???? ,
∵函数y=x+a与y=-2x+b的交点坐标为(-2,1),
∴方程组的解为: ????=?????????=???? ,
故答案为: ????=?????????=???? .
?
一十.一次函数与二元一次方程
32.某市出租车白天的收费起步价为14元,即路程不超过3公里时收费14元,超过部分每公里收费2.4元.如果乘客白天乘坐出租车的路程x(x>3)公里,乘车费为y元,那么y与x之间的关系式为 _______________ .
【解析】解:依题意有:y=14+2.4(x-3)=2.4x+6.8.
故答案为:y=2.4x+6.8.
y=2.4x+6.8
一十一根据实际问题列一次函数关系式
33.已知某汽车装满油后油箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,油箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶 _____ 千米,就应该停车加油.
【解析】解:设该一次函数解析式为y=kx+b,
将(400,10)、(500,0)代入y=kx+b中,
????????????????+????=????????????????????????+????=???? ,解得: ????=?????.????????=???????? ,
?
450
一十二一次函数的应用
∴该一次函数解析式为y=-0.1x+50.
当y=-0.1x+50=5时,x=450.
故答案为:450
34.元朝朱世杰的《算学启蒙》一书记载了一个数学问题:“良马日行二百四十里,舞马日行一百五十里,母马先行一十二日,问良马几何追及之.”它的大意是:“良马每天行240里,劣马每天行150里,劣马先行12天,良马需要多少天才能追上劣马?”如图,是良马与每马行走路程s(单位:里)关于行走时间t(单位:日)的函数图象
(1)射线OA记为S1,射线BA记为S2那么良马行走路程S关于行走时间t的函数图象是 ;(填S?或S2)
(2)两图象交点A的坐标是 ;
(3)求良马行走路程S关于行走时间t的函数解析式.
【解析】解:(1)根据题意,良马行走路程S关于行走时间t的函数图象是S2,
故答案为:S2;
(2)∵ ????????×????????????????????????????????????? =20(天),20+12=32(天),20×240=4800(里),
∴两图象交点A的坐标是(32,4800);
故答案为:(32,4800);
(3)根据题意,S=240(t-12)=240t-2880,
∴良马行走路程S关于行走时间t的函数解析式为S=240t-2880.
?
35.我们知道,海拔高度每上升1千米,温度下降6℃.某时刻,上海地面温度为20℃,设高出地面x千米处的温度为y℃.
(1)写出y与x之间的函数关系式,并写出函数定义域;
(2)有一架飞机飞过浦东上空,如果机舱内仪表显示飞机外面的温度为-166℃,求此刻飞机离地面的高度为多少千米?
【解析】解:(1)由题意得y=20-6x,
∴y与x之间的函数关系式是y=20-6x(x≥0).
(2)将y=-166代入y=20-6x,得-166=20-6x,解得x=31.
∴此刻飞机离地面的高度为31千米.
36.如图,lA与lB分别是根据A步行与B骑自行车在同一路上行驶的路程S与时间t的关系式所作出的图象,根据图象填空.
(1)B出发骑了一段路后,自行车发生故障进行修理,所用的时间是 小时;B从起点出发后 小时与A相遇;
(2)如果B的自行车没有发生故障,保持出发时的速度前进, 小时与A相遇,相遇点离B的出发点 千米.
【解析】解:(1)在图中发现0.5至1.5小时,自行车没有行走,
∴修理所用的时间为1小时,
图中两直线的交点是B与A相遇的时刻,
∴出发3小时后与A相遇.
故答案为:1,3;
(2)设B的自行车不发生故障时,函数解析式为S=k1t,
根据题意得:7.5=0.5k1,
解得:k1=15,
∴B的自行车不发生故障,函数解析式为S=15t,
设lA的解析式为:S=k2t+b,
由题意得: ????=????????????????????+????=???????? ,
?
解得: ????=????????=???????? ,
∴lA的解析式为:S=4t+10,
由 ????=????????????????=????????+???????? 解得: ????=????????????????????=???????????????????? .
∴B的自行车没有发生故障,保持出发时的速度前进, ???????????????? 小时与A相遇,相遇点离B的出发点 ???????????????????? 千米.
故答案为: ???????????????? , ???????????????????? .
?
37.一辆货车从甲地出发运送物资到乙地,稍后一辆轿车从甲地运送乘客到乙地,货车行驶的平均速度是60千米/小时,两车行驶了120千米之后同时进入加油站,从甲地到加油站这段路程中,两车离甲地的路程y(千米)与时间x(小时)的函数图象如图所示:
(1)a的值为 _____ ;
(2)轿车的速度为 ____ 千米/小时;
(3)加完油后,货车和轿车按照各自原来的行驶速度同时从加油站出发前往乙地,轿车比货车早 15 个小时到达乙地,求加油站和乙地间的距离.
?
0.5
80
【解析】解:(1)由题意可得,a=30÷60=0.5,故答案为:0.5;
(2)货车到达加油站所用的时间为:120÷60=2(h),
轿车所用时间为:2-0.5=1.5(h),
轿车的速度120÷1.5=80(千米/小时),
故答案为:80;
(3)设轿车到达乙地的时间为x小时,则货车到达乙地的时间为(x+ ???????? )小时,80(x-0.5)=60?(x+ ???????? ),
?
解得x=2.6,
∴加油站和乙地间的距离80(2.6-0.5)-120=48(千米).
答:加油站和乙地间的距离为48千米.
38.在创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间的关系的部分图象,请解答下列问题.
____
(1)乙队在2≤x≤6的时段内的速度是 ____ 米/时,当甲队铺了50米时,乙队铺了 ____ 米.
(2)如果铺设的彩色道砖的总长度为150米,开挖6小时后,甲队,乙队均增加人手,提高了工作效率,此后乙队平均每小时比甲队多铺5米,结果乙队反而比甲队提前1小时完成总铺设任务.求提高工作效率后甲队、乙队每小时铺设的长度分别为多少米?
5
45
【解析】解:(1)由图象可得,
乙队在2≤x≤6的时段内的速度是:(50-30)÷(6-2)=5(米/时);
甲队在0≤x≤6的时段内的速度是:60÷6=10(米/时),
当甲队铺了50米时,时间= ???????????????? =5(时),
则乙队铺了30+5×(5-2)=30+5×3=45(米),
故答案为:5,45;
?
(2)设提高工作效率后甲队每小时铺设的长度为x米,则乙队每小时铺设的长度为(x+5)米,根据题意得,
??????????????????????????????=?????????????????????????+???? ,
解得x1=15,x2=-30,
经检验,x1=15,x2=-30,
均为原方程的解,但x2=-30不合题意,舍去,
所以提高工作效率后甲队每小时铺设的长度为15米,乙队每小时铺设的长度为20米.
?
39.本区某住宅小区物业欲购买杨树、香樟树两种树苗共600棵,已知杨树每棵树苗40元,香樟树每棵树苗50元.
(1)设购买香樟树为x棵,购买树苗的总费用为y元,求出y与x之间的函数关系式,并写出x的取值范围;
(2)某植树队负责种植这些树苗,如果现计划每天比原计划多种植10棵,那么可提前3天完成种植任务,求现计划平均每天种植树苗的棵数.
【解析】解:(1)由题意可得,y=50x+(600-x)×40=10x+24000,
即y与x之间的函数关系式是y=10x+24000(0≤x≤600);
(2)设现计划平均每天种植树苗a棵, ????????????????+????=????????????????????????? ,
解得,a=50或a=-40(舍去),
检验:当a=50时,a(a-10)≠0,
故原分式方程的解是a=50,
答:现计划平均每天种植树苗50棵.
?
40.如图是某辆汽车加满油后,油箱剩油量y(升)关于已行驶路程x(千米)的函数图象(由两条线段构成).
(1)根据图象,当油箱剩油量为26升时,汽车已行驶的路程为 _____ 千米;当0≤x≤240时,消耗一升油汽车能行驶的路程为 ____ 千米.
(2)当240≤x≤420时,求y关于x的函数表达式,并计算当汽车已行驶300千米时油箱的剩油量.
【解析】解:(1)由图象可得,当油箱剩油量为26升时汽车已行驶的路程为240千米,
240
10
∵240÷(50-26)=10(千米/升),
∴消耗一升油汽车能行驶的路程为10千米.
故答案为:240,10;
(2)设y=kx+b,把(240,26)和(420,11)代入可得,
????????????????+????=????????????????????????+????=???????? ,解得 ????=?????????????????=???????? ,
∴函数表达式为y=- ???????????? x+46,
?
当x=300时,y=- ???????????? ×300+46=21,
答:y关于x的函数表达式为y=- ???????????? x+46,当汽车已行驶300千米时油箱的剩油量是21升.
?
41.有甲乙两个均装有进水管和出水管的容器,初始时,两容器同时开进水管,甲容器到8分钟时,关闭进水管打开出水管;到16分钟时,又打开了进水管,此时既进水又出水,到28分钟时,同时关闭两容器的所有水管.两容器每分钟进水量与出水量均为常数,容器的水量y(升)与时间x(分)之间的函数关系如图所示,解答下列问题:
(1)甲容器的进水管每分钟进水 ____ 升,出水管每分钟出水 _____ 升.
(2)求乙容器内的水量y与时间x的函数关系式.
(3)
5
2.5
求从初始时刻到两容器最后一次水量相等时所需的时间.
【解析】解:(1)进水管的速度为:40÷8=5(升/分),
出水管的速度为:(40-20)÷(16-8)=2.5(升/分).
故答案为:5,2.5;
(2)设y与时间x的函数关系式为y=k1x+b1,由图象可知(0,10),(5,15)在函数图象上,
∴ ????????=????????????????????+????????=???????? 解得: ????????=????????????=???????? .
∴y=x+10;
?
(3)由图象可知从初始时刻到两容器最后一次水量相等时所需的时间在16-28分之间,
∵5-2.5=2.5,20+2.5(28-16)=50,
∴当x=28时,y=50,
设y=kx+b,(k≠0),把(16,20),(28,50)代入上式得,
????????????+????=????????????????????+????=???????? ,解得: ????=????.????????=????????? ,∴y=2.5x-20,
由题意得:x+10=2.5x-20,解得:x=20.
∴初始时刻到两容器最后一次水量相等时所需的时间为20分钟.
?
课堂小结:
1、通过学习,我们理解了一次函数的概念,认识和研究了函数的图像和性质,学会了一次函数的实际应用,并通过一次函数的图像揭示一元一次方程的根与一元一次不等式的解集的联系。
2、在运用待定系数法,求一次函数解析式时,只要在k、b、直线上点的坐标或面积等条件中,给定两个独立条件,或根据图像,就可求出它的表达式.
3、要 善于捕捉图像中的所有信息,并能够熟练地转化成实际问题。
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 20章 一次函数
一.一次函数的定义
二.一次函数的图象
三.一次函数的性质
四.一次函数图象与系数的关系
五.一次函数图象上点的坐标特征
六.一次函数图象与几何变换
七.待定系数法求一次函数解析式
八.一次函数与一元一次方程
九.一次函数与一元一次不等式
一十.一次函数与二元一次方程
一十一根据实际问题列一次函数关系式
一十二一次函数的应用
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
当k=0时,函数y=b(b是常数)叫做______函数。
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
1
k≠0
2、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
b
一条直线
常值
要点回顾
3、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图,回答各图中k、b的符号:
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
增大
减小
4、如果直线y=k1x+b1与直线y=k2x+b2平行,那么_________________。
k1=k2且b1≠b2
1.下列函数中,是一次函数的是( ____ )
A.y= 12???? +1 B.y=2x+1
C.y=x2+1 D.y=kx+b(k、b是常数)
?
【解析】解:A选项的分母中有未知数,不是整式,故该选项不符合题意;
B选项符合y=kx+b(k≠0)的形式,故该选项符合题意;
C选项是二次函数,故该选项不符合题意;
D选项没有强调k≠0,故该选项不符合题意;
B
一.一次函数的定义
故选:B.
2.下列函数中,y是x的一次函数的是( ____ )
A.y=x2-5 B.y=3
C.y=kx+b D.y=x-1
【解析】解:A、自变量x的次数是2,不是一次函数,故此选项不符合题意;
B、没有自变量,不是一次函数,故此选项不符合题意;
C、自变量x的系数k可能为0,故此选项不符合题意;
D、是一次函数,故此选项符合题意;
D
故选:D.
3.在直角坐标平面内,一次函数y=ax+b的图象如图所示,那么下列说法正确的是( ____ )
A.当x>0时,y>-2 B.当x<1时,y>0
C.当x<0时,-2<y<0 D.当x≥1时,y≤0
【解析】解:由函数y= ???????? x+3的图象可知,
当x>0时,y>-2,故A正确;
当x<1时,y<0,B选项错误;
当x<0时,y<-2,C选项错误;
?
A
二.一次函数的图象
当x≥1时,y≥0,故D错误.
故选:A.
4.如图,若k?b>0,且b+k>0,则一次函数y=kx+b的大致图象是( ____ )
A.___B.___ C. D.
A
【解析】解:∵k?b>0,且b+k>0,∴k>0,b>0,
∴一次函数y=kx+b的图象经过第一、二、三象限,
故选:A.
5.如图是一次函数y=kx+b的图象,当x _____ 时,函数图象在x轴的上方.
>-2
【解析】解:当x>-2时,函数图象在x轴的上方,
故答案为:>-2.
6.如果ab<0,ac<0,则直线 ????=?????????????????????? 不经过( ____ )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
?
【解析】解:∵ab<0,ac<0,
∴a,b异号,a,c异号,
∴ ?????????>???? ,且b,c同号,
∴ ?????????<???? ,
?
B
三.一次函数的性质
一次函数 ????=?????????????????????? 的图象经过第一、三、四象限,不经过第二象限.故选:B.
?
7.一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是 _____ .
【解析】解:由图象可得,
当y>0时,x的取值范围是x<2,
故答案为:x<2.
x<2
8.已知点A(x1,y1)、B(x2,y2)都在直线y=-x+3上,如果x1<x2,那么y1 ____ y2(填“>”“<”或“=”).
【解析】解:∵k=-1<0,
∴y随x的增大而减小,
又∵点A(x1,y1)、B(x2,y2)都在直线y=-x+3上,且x1<x2,
∴y1>y2.
故答案为:>.
>
9.一次函数 ????=12?????1 的图象不经过的象限是( ____ )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
?
【解析】解:∵y= ???????? x-1,
∴k= ???????? >0,图象经过第一、三象限,
b=-1<0,直线与y轴负半轴相交,图象经过第四象限,
?
B
四.一次函数图象与系数的关系
即一次函数y= ???????? x-1的图象经过第一、三、四象限,不经过第二象限.
故选:B.
?
10.直线y=( 12 k-1)x+2(1-k)的图象经过第一、二、四象限,那么k的取值范围是( ____ )
A.k>2 B.k<2 C.k>1 D.k<1
?
【解析】解:∵直线y=( ???????? k-1)x+2(1-k)的图象经过第一、二、四象限,
?
D
∴ ?????????????????<????????(?????????)>???? ,
解得k<1.
故选:D.
?
11.若一次函数y=kx+b的函数值y随x的增大而减小,且图象与y轴的负半轴相交,那么对k和b的符号判断正确的是( ____ )
A.k>0,b>0
B.k>0,b<0
C.k<0,b>0
D.k<0,b<0
【解析】解:∵一次函数y=kx+b的函数值y随x的增大而减小,∴k<0;
∵图象与y轴的负半轴相交,∴b<0.
故选:D.
D
12.如果一次函数y=(m-3)x-1的函数值y随着x的值增大而减小,那么m取值范围是 _____ .
【解析】解:∵一次函数y=(m-3)x-1的函数值y随着x的值增大而减小,
∴m-3<0,
∴m<3;
故答案为:m<3.
m<3
13.如果直线y=(2m+1)x-2+m经过第一、三、四象限,那么则m的取值范围是 .
【解析】解:∵直线y=(2m+1)x-2+m经过第一、三、四象限,
∴ ????????+????>?????????+????<???? ,
解得:- ???????? <m<2,
∴m的取值范围为- ???????? <m<2.
故答案为:- ???????? <m<2.
?
14.直线y=-x+6与x轴的交点是 ________ .
【解析】解:当y=0时,-x+6=0,
解得:x=6,
∴直线y=-x+6与x轴的交点是(6,0).
故答案为:(6,0).
(6,0)
五.一次函数图象上点的坐标特征
15.已知直线y=kx-3与两坐标轴所围成的三角形的面积为6,
则k的值为 .
【解析】解:依照题意,画出图象,如图所示.
当x=0时,y=kx-3=-3,∴点B的坐标为(0,-3);
当y=0时,kx-3=0,解得:x= ???????? ,
∴点A的坐标为( ???????? ,0).
?
∴S△AOB= ???????? ×3×| ???????? |=6,
解得:k=± ???????? .
故答案为:± ???????? .
?
16.已知一次函数y=kx+1的图象经过点A(2,5),那么k= ____ .
【解析】解:∵一次函数y=kx+1的图象经过点(2,5),
∴5=2k+1,
解得k=2.
故答案为:2.
2
17.在平面直角坐标系xOy中,对于P、Q两点给出如下定义:如果点P到x、y轴的距离中的最小值等于点Q到x、y轴的距离中的最小值,那么称P、Q两点为“坐标轴等距点”,例如点P(2,2)与点Q(-2,-3)为“坐标轴等距点”.已知点A的坐标为(-3,2),如果点B在直线y=x-1上,且A、B两点为“坐标轴等距点”,那么点B的坐标为 _____________________ .
【解析】解:∵点A的坐标为(-3,2),
∴点A到x、y轴的距离中的最小值为2,
∵A、B两点为“坐标轴等距点”,
∴点B到x、y轴的距离中的最小值为2.
当x=-2时,y=-2-1=-3,|-3|>|-2|,
(-2,-3)或(3,2)
∴点B到x、y轴的距离中的最小值为2,
∴点B的坐标为(-2,-3);
当x=2时,y=2-1=1,|1|<|2|,
∴点B到x、y轴的距离中的最小值为1,不符合题意,舍去;
当y=-2时,x-1=-2,
解得:x=-1,
∵|-1|<|-2|,
∴点B到x、y轴的距离中的最小值为1,不符合题意,舍去;
当y=2时,x-1=2,
解得:x=3,
∵|3|>|2|,
∴点B到x、y轴的距离中的最小值为2,
∴点B的坐标为(3,2).
综上所述,点B的坐标为(-2,-3)或(3,2).
故答案为:(-2,-3)或(3,2).
18.如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=- 12 x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 .
?
【解析】解:①当∠ABD=90°时,如图1,则∠DBC+∠ABO=90°,
∴∠DBC=∠BAO,
由直线y=- ???????? x+b交线段OC于点B,交x轴于点A可知OB=b,OA=2b,
?
∵点C(0,4),
∴OC=4,
∴BC=4-b,
在△DBC和△BAO中,
∠????????????=∠????????????∠????????????=∠????????????????????=????????
∴△DBC≌△BAO(AAS),
∴BC=OA,
即4-b=2b,
?
∴b= ???????? ;
②当∠ADB=90°时,如图2,
作AF⊥CE于F,
同理证得△BDC≌△DAF,
∴CD=AF=4,BC=DF,
∵OB=b,OA=2b,
∴BC=DF=2b-4,
∵BC=4-b,
∴2b-4=4-b,
∴b= ???????? ;
?
③当∠DAB=90°时,如图3,
作DF⊥OA于F,
同理证得△AOB≌△DFA,
∴OA=DF,
∴2b=4,
∴b=2;
综上,b的值为 ???????? 或 ???????? 或2.
故答案为 ???????? 或 ???????? 或2.
?
19.把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,已知点A(1,0),B(4,0),现将Rt△ABC沿着x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( ____ )
A.4
B.8
C.16
D.8 2
?
【解析】解:如图所示.
C
___
∵点A、B的坐标分别为(1,0)、(4,0),
∴AB=3.
∵∠CAB=90°,BC=5,
∴AC=4.
∴A′C′=4.
∵点C′在直线y=2x-6上,
∴2x-6=4,解得 x=5.
即OA′=5.
∴CC′=5-1=4.
∴S?BCC′B′=4×4=16.
即线段BC扫过的面积为16.
故选:C.
20.已知:直线 ????=?12????+32 与x轴交于点M,与y轴交于点N,将△MON绕着坐标原点逆时针旋转90°,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.
?
【解析】解:(1)对于直线 ????=?????????????+???????? ,
令y=0得 ????=?????????????+???????? ,解得x=3,
令x=0,得 ????=???????? ,
?
∴直线 ????=?????????????+???????? 与x轴交于点M,与y轴交于点N,
∴OM=3,ON= ???????? ,
∵将△MON绕着坐标原点逆时针旋转90°,与x轴交于点A,与y轴交于点B,
∴OA=ON= ???????? ,OB=OM=3,
∴ ????(?????????,????) ,B(0,3);
?
____
(2)∵OA= ???????? ,OP=2OA,
∴OP=3,
∵过B点作直线BP与x轴交于点P,
∴P(-3,0)或P(3,0),
∵OB=3,
?
∴当P(-3,0)时, ????△????????????=????????×????????×????????=????????×|?????????????|×????=???????? ;
当P(3,0)时, ????△????????????=????????×????????×????????=????????×|????+????????|×????=???????????? .
____
?
21.把直线y=-2x+4向左平移3个单位后,在y轴上的截距为 ____ .
【解析】解:由“左加右减”的原则可知,把直线y=-2x+4向左平移3个单位后所得直线的解析式为y=-2(x+3)+4,即y=-2x-2,
∵把直线y=-2x+4向左平移3个单位后,在y轴上的截距为-2,
故答案为:-2.
-2
六.一次函数图象与几何变换
22.如果把直线y=3x-1沿y轴向下平移3个单位,所得直线的解析式是 _________ .
【解析】解:把直线y=3x-1沿y轴向下平移3个单位,所得直线的解析式是y=3x-4;
故答案为:y=3x-4.
y=3x-4
23.将直线y=2x+1平移,使平移后的直线经过点(0,-3),所得直线的表达式是 _________ .
【解析】解:设平移后的函数表达式是y=2x+b,
∵它经过点(0,-3),
∴-3=b,
解得:b=-3.
∴平移后的函数解析式为:y=2x-3.
故答案为:y=2x-3.
y=2x-3
24.已知一次函数y=kx+b(k≠0)的图象经过点(2,0)与(0,4),那么y随着x的增大而 _____ .(填“增大”或“减小”)
【解析】解:(方法一)将(2,0),(0,4)代入y=kx+b得: ????????+????=????????=???? ,解得: ????=?????????=???? ,
∵k=-2<0,∴y随x的增大而减小.
故答案为:减小.
(方法二)依照题意画出函数图象,如图所示.
?
减小
七.待定系数法求一次函数解析式
观察函数图象,可知:y随x的增大而减小.
故答案为:减小.
25.已知y+2与3x成正比例,当x=1时,y的值为4.
(1)求y与x之间的函数表达式;
(2)求该函数图象与坐标轴围成的三角形周长.
【解析】解:(1)∵y+2与3x成正比例,
∴设y+2=k?3x,
∵当x=1时,y的值为4,
∴4+2=3k,
∴k=2,
∴y+2=6x,
∴y与x之间的函数表达式是y=6x-2,
(2)如图,直线y=6x-2与x、y轴分别交于A、B两点,
当x=0时,y=-2,当y=0时,x= ???????? ,
∴A的坐标是( ???????? ,0),B的坐标是(0,-2),
∴AO= ???????? ,OB=2,
∴AB= ????????????+???????????? = ????????+(????????)???? = ???????????? ,
∴函数图象与坐标轴围成的三角形周长是OA+OB+AB= ???????? +2+ ???????????? = ????+????????????
?
26.已知函数y=f(x)满足当a1≤x≤b1时,对应的函数值y的范围是a1≤y≤b1,我们称该函数为关于a1和b1的方块函数.如果一次函数y=kx+b(k、b为常数,k≠0)是关于1和2的方块函数,且它的图象不经过原点,那么该一次函数的解析式为 _________ .
【解析】解:当x=1时,y=k+b;当x=2时,y=2k+b,
①当 ????+????=????????????+????=???? 时,解得 ????=????????=???? ,∴y=x,不合题意,舍去;
②当 ????+????=????????????+????=???? 时,解得 ????=?????????=???? ,∴y=-x+3;
?
y=-x+3
∴一次函数的解析式为y=-x+3,故答案为:y=-x+3.
27.如图,在直角坐标平面内,△ABC的顶点A(-1,0),点B与点A关于原点对称,AB=BC,∠CAB=30°,将△ABC绕点C旋转,使点A落在x轴上的点D处,点B落在点E处,那么BE所在直线的解析式为 .
【解析】解:如图,过点C作CF⊥x轴于点F,
∵△ABC的顶点A(-1,0),点B与点A关于原点对称,
∴B(1,0),
∴AB=2.
∵AB=BC,∠CAB=30°,
∴BC=AB=2,
∴CF=BC?sin60°=2× ???????? = ???? ,BF=BC?cos30°=2× ???????? =1,
∴C(2, ???? ).
∵将△ABC绕点C旋转,使点A落在x轴上的点D处,点B落在点E处,
∴AB=CE=2,
∴E(4, ???? ).
设直线BE的解析式为y=kx+b(k≠0),
?
∴ ????+????=????????????+????=???? ,解得 ????=????????????=????????? ,
∴BE所在直线的解析式为:y= ???????? x- ???????? .
故答案为:y= ???????? x- ???????? .
?
28.一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为 ______ .
【解析】解:从图象上可知则关于x的方程kx+b=0的解为的解是x=-2.
故答案为:x=-2
x=-2
八.一次函数与一元一次方程
29.直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为 ______ .
【解析】解:两个条直线的交点坐标为(-1,3),且当x>-1时,直线l1在直线l2的上方,故不等式k2x>k1x+b的解集为x<-1.
故本题答案为:x<-1.
x<-1
九.一次函数与一元一次不等式
30.如图,直线y=kx+b经过点(-2,0)和(0,1),那么关于x的不等式kx+b>0的解集为 ______ .
【解析】解:根据函数图象可知,
∴关于x的不等式kx+b>0的解集为x>-2.
故答案为:x>-2.
x>-2
31.已知函数y=x+a与y=-2x+b的交点坐标为(-2,1),则方程组 ?????????=?????2????+????=???? 的解为 .
?
【解析】解:方程组 ?????????=?????????????+????=???? 可变为: ????=????+????????=?????????+???? ,
∵函数y=x+a与y=-2x+b的交点坐标为(-2,1),
∴方程组的解为: ????=?????????=???? ,
故答案为: ????=?????????=???? .
?
一十.一次函数与二元一次方程
32.某市出租车白天的收费起步价为14元,即路程不超过3公里时收费14元,超过部分每公里收费2.4元.如果乘客白天乘坐出租车的路程x(x>3)公里,乘车费为y元,那么y与x之间的关系式为 _______________ .
【解析】解:依题意有:y=14+2.4(x-3)=2.4x+6.8.
故答案为:y=2.4x+6.8.
y=2.4x+6.8
一十一根据实际问题列一次函数关系式
33.已知某汽车装满油后油箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,油箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶 _____ 千米,就应该停车加油.
【解析】解:设该一次函数解析式为y=kx+b,
将(400,10)、(500,0)代入y=kx+b中,
????????????????+????=????????????????????????+????=???? ,解得: ????=?????.????????=???????? ,
?
450
一十二一次函数的应用
∴该一次函数解析式为y=-0.1x+50.
当y=-0.1x+50=5时,x=450.
故答案为:450
34.元朝朱世杰的《算学启蒙》一书记载了一个数学问题:“良马日行二百四十里,舞马日行一百五十里,母马先行一十二日,问良马几何追及之.”它的大意是:“良马每天行240里,劣马每天行150里,劣马先行12天,良马需要多少天才能追上劣马?”如图,是良马与每马行走路程s(单位:里)关于行走时间t(单位:日)的函数图象
(1)射线OA记为S1,射线BA记为S2那么良马行走路程S关于行走时间t的函数图象是 ;(填S?或S2)
(2)两图象交点A的坐标是 ;
(3)求良马行走路程S关于行走时间t的函数解析式.
【解析】解:(1)根据题意,良马行走路程S关于行走时间t的函数图象是S2,
故答案为:S2;
(2)∵ ????????×????????????????????????????????????? =20(天),20+12=32(天),20×240=4800(里),
∴两图象交点A的坐标是(32,4800);
故答案为:(32,4800);
(3)根据题意,S=240(t-12)=240t-2880,
∴良马行走路程S关于行走时间t的函数解析式为S=240t-2880.
?
35.我们知道,海拔高度每上升1千米,温度下降6℃.某时刻,上海地面温度为20℃,设高出地面x千米处的温度为y℃.
(1)写出y与x之间的函数关系式,并写出函数定义域;
(2)有一架飞机飞过浦东上空,如果机舱内仪表显示飞机外面的温度为-166℃,求此刻飞机离地面的高度为多少千米?
【解析】解:(1)由题意得y=20-6x,
∴y与x之间的函数关系式是y=20-6x(x≥0).
(2)将y=-166代入y=20-6x,得-166=20-6x,解得x=31.
∴此刻飞机离地面的高度为31千米.
36.如图,lA与lB分别是根据A步行与B骑自行车在同一路上行驶的路程S与时间t的关系式所作出的图象,根据图象填空.
(1)B出发骑了一段路后,自行车发生故障进行修理,所用的时间是 小时;B从起点出发后 小时与A相遇;
(2)如果B的自行车没有发生故障,保持出发时的速度前进, 小时与A相遇,相遇点离B的出发点 千米.
【解析】解:(1)在图中发现0.5至1.5小时,自行车没有行走,
∴修理所用的时间为1小时,
图中两直线的交点是B与A相遇的时刻,
∴出发3小时后与A相遇.
故答案为:1,3;
(2)设B的自行车不发生故障时,函数解析式为S=k1t,
根据题意得:7.5=0.5k1,
解得:k1=15,
∴B的自行车不发生故障,函数解析式为S=15t,
设lA的解析式为:S=k2t+b,
由题意得: ????=????????????????????+????=???????? ,
?
解得: ????=????????=???????? ,
∴lA的解析式为:S=4t+10,
由 ????=????????????????=????????+???????? 解得: ????=????????????????????=???????????????????? .
∴B的自行车没有发生故障,保持出发时的速度前进, ???????????????? 小时与A相遇,相遇点离B的出发点 ???????????????????? 千米.
故答案为: ???????????????? , ???????????????????? .
?
37.一辆货车从甲地出发运送物资到乙地,稍后一辆轿车从甲地运送乘客到乙地,货车行驶的平均速度是60千米/小时,两车行驶了120千米之后同时进入加油站,从甲地到加油站这段路程中,两车离甲地的路程y(千米)与时间x(小时)的函数图象如图所示:
(1)a的值为 _____ ;
(2)轿车的速度为 ____ 千米/小时;
(3)加完油后,货车和轿车按照各自原来的行驶速度同时从加油站出发前往乙地,轿车比货车早 15 个小时到达乙地,求加油站和乙地间的距离.
?
0.5
80
【解析】解:(1)由题意可得,a=30÷60=0.5,故答案为:0.5;
(2)货车到达加油站所用的时间为:120÷60=2(h),
轿车所用时间为:2-0.5=1.5(h),
轿车的速度120÷1.5=80(千米/小时),
故答案为:80;
(3)设轿车到达乙地的时间为x小时,则货车到达乙地的时间为(x+ ???????? )小时,80(x-0.5)=60?(x+ ???????? ),
?
解得x=2.6,
∴加油站和乙地间的距离80(2.6-0.5)-120=48(千米).
答:加油站和乙地间的距离为48千米.
38.在创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间的关系的部分图象,请解答下列问题.
____
(1)乙队在2≤x≤6的时段内的速度是 ____ 米/时,当甲队铺了50米时,乙队铺了 ____ 米.
(2)如果铺设的彩色道砖的总长度为150米,开挖6小时后,甲队,乙队均增加人手,提高了工作效率,此后乙队平均每小时比甲队多铺5米,结果乙队反而比甲队提前1小时完成总铺设任务.求提高工作效率后甲队、乙队每小时铺设的长度分别为多少米?
5
45
【解析】解:(1)由图象可得,
乙队在2≤x≤6的时段内的速度是:(50-30)÷(6-2)=5(米/时);
甲队在0≤x≤6的时段内的速度是:60÷6=10(米/时),
当甲队铺了50米时,时间= ???????????????? =5(时),
则乙队铺了30+5×(5-2)=30+5×3=45(米),
故答案为:5,45;
?
(2)设提高工作效率后甲队每小时铺设的长度为x米,则乙队每小时铺设的长度为(x+5)米,根据题意得,
??????????????????????????????=?????????????????????????+???? ,
解得x1=15,x2=-30,
经检验,x1=15,x2=-30,
均为原方程的解,但x2=-30不合题意,舍去,
所以提高工作效率后甲队每小时铺设的长度为15米,乙队每小时铺设的长度为20米.
?
39.本区某住宅小区物业欲购买杨树、香樟树两种树苗共600棵,已知杨树每棵树苗40元,香樟树每棵树苗50元.
(1)设购买香樟树为x棵,购买树苗的总费用为y元,求出y与x之间的函数关系式,并写出x的取值范围;
(2)某植树队负责种植这些树苗,如果现计划每天比原计划多种植10棵,那么可提前3天完成种植任务,求现计划平均每天种植树苗的棵数.
【解析】解:(1)由题意可得,y=50x+(600-x)×40=10x+24000,
即y与x之间的函数关系式是y=10x+24000(0≤x≤600);
(2)设现计划平均每天种植树苗a棵, ????????????????+????=????????????????????????? ,
解得,a=50或a=-40(舍去),
检验:当a=50时,a(a-10)≠0,
故原分式方程的解是a=50,
答:现计划平均每天种植树苗50棵.
?
40.如图是某辆汽车加满油后,油箱剩油量y(升)关于已行驶路程x(千米)的函数图象(由两条线段构成).
(1)根据图象,当油箱剩油量为26升时,汽车已行驶的路程为 _____ 千米;当0≤x≤240时,消耗一升油汽车能行驶的路程为 ____ 千米.
(2)当240≤x≤420时,求y关于x的函数表达式,并计算当汽车已行驶300千米时油箱的剩油量.
【解析】解:(1)由图象可得,当油箱剩油量为26升时汽车已行驶的路程为240千米,
240
10
∵240÷(50-26)=10(千米/升),
∴消耗一升油汽车能行驶的路程为10千米.
故答案为:240,10;
(2)设y=kx+b,把(240,26)和(420,11)代入可得,
????????????????+????=????????????????????????+????=???????? ,解得 ????=?????????????????=???????? ,
∴函数表达式为y=- ???????????? x+46,
?
当x=300时,y=- ???????????? ×300+46=21,
答:y关于x的函数表达式为y=- ???????????? x+46,当汽车已行驶300千米时油箱的剩油量是21升.
?
41.有甲乙两个均装有进水管和出水管的容器,初始时,两容器同时开进水管,甲容器到8分钟时,关闭进水管打开出水管;到16分钟时,又打开了进水管,此时既进水又出水,到28分钟时,同时关闭两容器的所有水管.两容器每分钟进水量与出水量均为常数,容器的水量y(升)与时间x(分)之间的函数关系如图所示,解答下列问题:
(1)甲容器的进水管每分钟进水 ____ 升,出水管每分钟出水 _____ 升.
(2)求乙容器内的水量y与时间x的函数关系式.
(3)
5
2.5
求从初始时刻到两容器最后一次水量相等时所需的时间.
【解析】解:(1)进水管的速度为:40÷8=5(升/分),
出水管的速度为:(40-20)÷(16-8)=2.5(升/分).
故答案为:5,2.5;
(2)设y与时间x的函数关系式为y=k1x+b1,由图象可知(0,10),(5,15)在函数图象上,
∴ ????????=????????????????????+????????=???????? 解得: ????????=????????????=???????? .
∴y=x+10;
?
(3)由图象可知从初始时刻到两容器最后一次水量相等时所需的时间在16-28分之间,
∵5-2.5=2.5,20+2.5(28-16)=50,
∴当x=28时,y=50,
设y=kx+b,(k≠0),把(16,20),(28,50)代入上式得,
????????????+????=????????????????????+????=???????? ,解得: ????=????.????????=????????? ,∴y=2.5x-20,
由题意得:x+10=2.5x-20,解得:x=20.
∴初始时刻到两容器最后一次水量相等时所需的时间为20分钟.
?
课堂小结:
1、通过学习,我们理解了一次函数的概念,认识和研究了函数的图像和性质,学会了一次函数的实际应用,并通过一次函数的图像揭示一元一次方程的根与一元一次不等式的解集的联系。
2、在运用待定系数法,求一次函数解析式时,只要在k、b、直线上点的坐标或面积等条件中,给定两个独立条件,或根据图像,就可求出它的表达式.
3、要 善于捕捉图像中的所有信息,并能够熟练地转化成实际问题。
