最新人教版七下数学 第八章 二元一次方程组 单元小结 课件(共37张PPT)
文档属性
| 名称 | 最新人教版七下数学 第八章 二元一次方程组 单元小结 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
二元一次方程组
单元小结
8
人教版·七年级下册
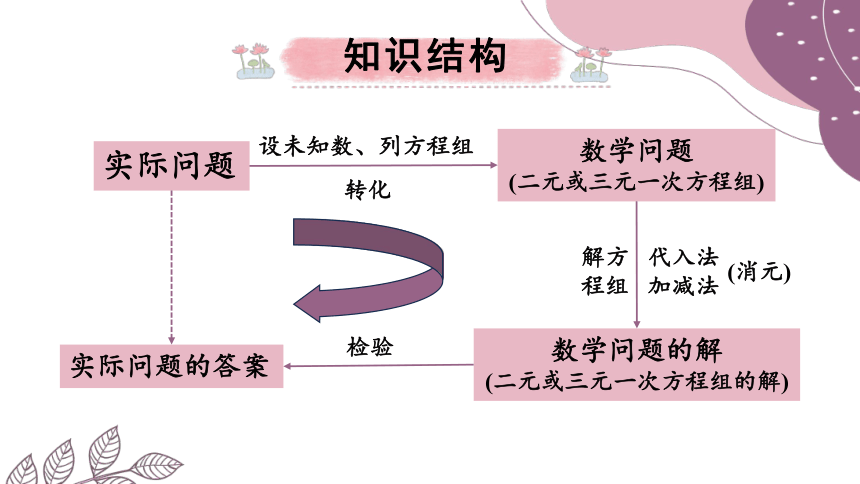
实际问题
数学问题
(二元或三元一次方程组)
实际问题的答案
数学问题的解
(二元或三元一次方程组的解)
设未知数、列方程组
转化
检验
解方程组
代入法
加减法
(消元)
知识结构
考点一 二元一次方程与二元一次方程组的定义
例1 若 x2m-1 + 5y3n-2m = 7 是关于 x、y 的二元一次方程,则 m = ,n = .
1
1
关于 x、y 的二元一次方程
2m - 1 = 1,
3n - 2m = 1.
m = 1,
n = 1.
理解定义
列方程组
解方程组求出参数值
含有两个未知数,并且含有未知数的项的次数都是1, 像这样的方程叫做二元一次方程.
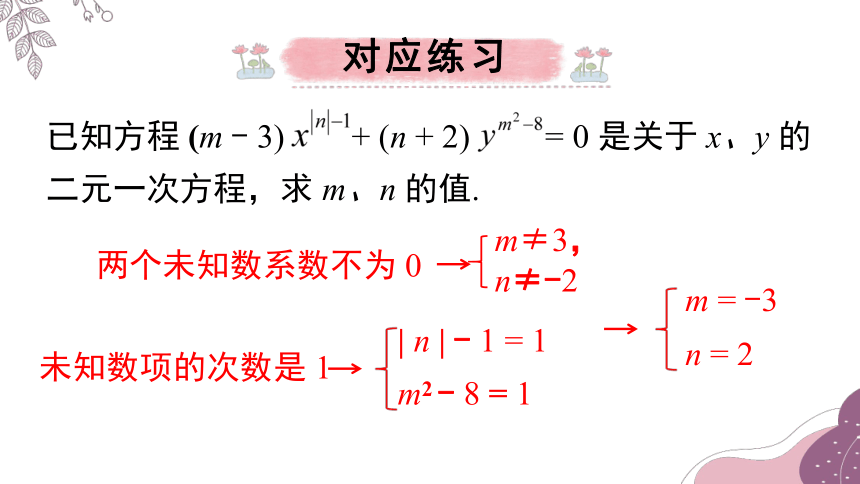
已知方程 (m - 3) + (n + 2) = 0 是关于 x、y 的二元一次方程,求 m、n 的值.
未知数项的次数是 1
| n | - 1 = 1
m2 - 8 = 1
m = -3
n = 2
两个未知数系数不为 0
m≠3,n≠-2
对应练习
考点二 二元一次方程与二元一次方程组的解
例2 已知 x = 1,y = -2 是关于 x、y 二元一次方程组
的解,求 a,b 的值.
解:
把 x = 1,y = -2 代入二元一次方程组得
a + 4 = 3,
1 + 2b = 4.
解得
a = -1
b = 1.5
ax - 2y = 3,
x - by = 4.
已知 x = 1,y = -2 满足 (ax - 2y - 3)2 + |x - by + 4| = 0,求 a + b 的值.
解:由题意可得
把 x = 1,y = -2 代入方程组可得
解得 ,则 a + b = -3.5.
ax - 2y - 3 = 0,
x - by + 4 = 0.
a + 4 - 3 = 0,
1 + 2b + 4 = 0.
a = -1
b = -2.5
对应练习
考点三 代入消元法与加减消元法
例3 用代入法消元法解方程组
解:
由①可得 y = 3x - 7 . ③
将③代入②得 5x + 2(3x - 7) = 8,
解得 x = 2. 把 x = 2 代入③得
y = -1.
由此可得二元一次方程组的解是
x = 2,
y = -1.
3x - y = 3,①
5x + 2y = 8.②
例4 用加减消元法解方程组
由② - ①得 18 = y + 11,解得 y = 7.
把 y = 7 代入①得 3x - 3 = 28 - 16,
解得 x = 5.
由此可得二元一次方程组的解为
x = 5,
y = 7.
解:
3( x–1 )=4( y–4 ),①
5( y–4 )=3( x+5 ). ②
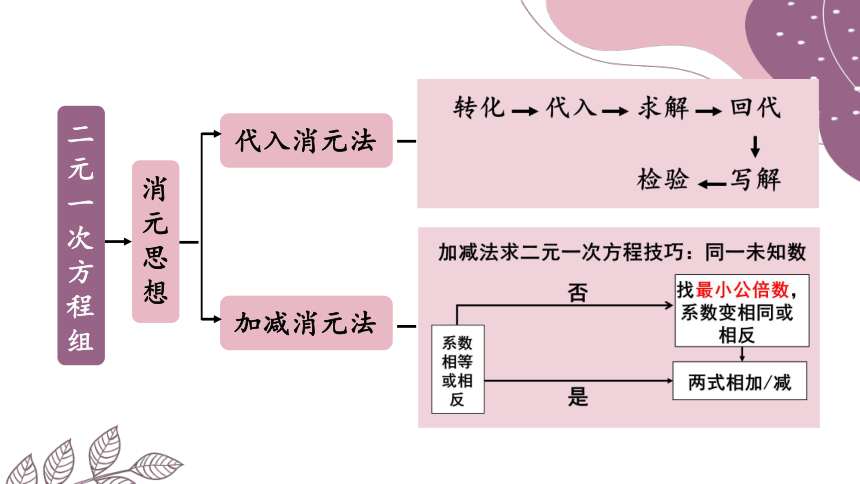
二元一次方程组
消元思想
代入消元法
加减消元法
已知 -4xm+nym-n 与 -2x7-my1+n 是同类项,求 m,n 的值.
解:由题意得
解得
m + n=7 - m ,
m - n=1 + n .
m=3,
n=1.
对应练习
考点四 二元一次方程组的实际应用
例5 把一些图书分给某班学生阅读,若每人分 3 本,则剩余 20 本;若每人分 4 本,则还缺 25 本. 这个班有多少学生?图书一共多少本?
等量关系:
3×学生人数+20=图书数量
4×学生人数-25=图书数量
设这个班有x名学生,图书一共有y本.
3x+20=y
4x-25=y
解:设该班有 x 名学生,图书一共有 y 本,则
答:这个班有 45 名学生,图书一共有 155 本.
解得
3x+20=y
4x-25=y
x=45
y=155
列二元一次方程组解决实际问题的步骤:
找等量关系
审题
设元
列方程组
解方程组
检验作答
2个未知数
根据等量关系
代入法
加减法
某校七年级安排宿舍,若每间宿舍住6人,则有4人住不下;若每间住7人,则有1间只住3人,且空余11间宿舍.问该年级寄宿学生有多少人?宿舍有多少间?
解:设该年级寄宿学生有 x 人,宿舍有 y 间.根据题意可得 解得
答:设该年级寄宿学生有514人,宿舍有85间.
6y+4=x
7×(y-11-1)=x-3
x=514
y=85
对应练习
1.用代入法解下列方程组:
(1)
a=2b+3
a=3b+20
(2)
x-y=13
x=6y-7
课堂练习
解:把①代入②,得2b+3=3b+20,解得b=-17
把b=-17代入①,得a=-31.
∴方程组的解为
a=-31
b=-17
①
②
解:把②代入①,
得6y-y-7=13,解得y=4
把y=4代入②,得x=17.
∴方程组的解为
x=17
y=4
①
②
【选自教材P111 复习题8 第1题】
(3)
x-y=4
4x+2y=-1
(4)
5x-y=110
9y-x=110
解:由①,得y=x-4 ③
把③代入②,得4x+2(x-4)=-1
解得
把 代入③,得
∴方程组的解为
①
②
解:由①,得y=5x-110 ③
把③代入②,
得9(5x-110)-x=110,解得x=25
把x=25代入③,得y=15.
∴方程组的解为
x=25
y=15
①
②
2.用加减法解下列方程组:
(1)
3m+b=11
-4m-b=11
(2)
0.6x-0.4y=1.1
0.2x-0.4y=2.3
解:①+②,得-m=22,
即m=-22.
把m=-22代入①,得b=77.
∴方程组的解为
m=-22
b=77
①
②
解:①-②,得0.4x=-1.2
解得x=-3,
把x=-3代入①,得
∴方程组的解为
①
②
x=-3
【选自教材P111 复习题8 第2题】
(3)
4f+g=15
3g-4f =-3
(4)
解:①+②,得4g=12,
解得g=3.
把g=3代入①,得f=3.
∴方程组的解为
f=3
g=3
①
②
解:①-②,得2y=-8,
解得y=-4.
把y=-4代入②,得x=12.
∴方程组的解为
x=12
y=-4
①
②
3.解下列方程组:
(1)
4(x-y-1)=3(1-y)-2
解:整理方程组,得
①×2+②,得11x=22,即x=2
把x=2代入①,得4×2-y=5
解得y=3
∴原方程组的解是
x=2
y=3
①
②
4x-y=5
3x+2y=12
【选自教材P111 复习题8 第3题】
3.解下列方程组:
(2)
6(x+y)-4(2x-y)=16
解:整理方程组,得
①×2+②×5,得-22y+50y=-24+80,解得y=2
把y=2代入①,得5x-11×2=-12
解得x=3
∴原方程组的解是
x=2
y=2
①
②
5x-11y=-12
-2x+10y=16
【选自教材P111 复习题8 第3题】
4.解系列方程组:
(1)
3x-y+z=3
2x+y-3z=11
x+y+z=12
③
原方程的解为
解:①+②,得5x-2z=14.④
②-③,得x-4z=-1.⑤
④与⑤组成方程组
①
②
5x-2z=14
x-4z=-1
把 , 代入③得
解得
解这个方程组得
【选自教材P111 复习题8 第4题】
(2)
5x-4y+4z=13
2x+7y-3z=19
3x+2y-z=18
4.解系列方程组:
解:①+②+③,得10x+5y=50.④
①+③×4 ,得17x+4y=85.⑤
④与⑤组成方程组
10x+5y=50
17x+4y=85
把x=5,y=0 代入③得
3×5-z=18,解得z=-3
解这个方程组得
原方程的解为
x=5
y=0
z=-3
③
①
②
x=5
y=0
【选自教材P111 复习题8 第4题】
5. 1号仓库与2号仓库共存粮450t.现从1号仓库运出存粮的60%,从2号仓库运出存粮的40%,结果2号仓库所余粮食比1号仓库所余粮食多30t.1号仓库与2号仓库原来各存粮多少吨?
【选自教材P111 复习题8 第5题】
解:设1号仓库原来存粮x t,2号仓库原来存粮y t.
根据题意,得
解得
x+y=450
(1-0.6)x=(1-0.4)y-30
x=240
y=210
答:1号仓库原来存粮240t,2号仓库原来存粮210t.
6.甲、乙二人都以不变的速度在环形路上跑步,如果同时同地出发,反向而行,每隔2min相遇一次;如果同时同地出发,同向而行,每隔6min相遇一次,已知甲比乙跑得快,甲、乙二人每分各跑多少圈?
【选自教材P111 复习题8 第6题】
解:设甲每分跑x 圈,乙每分跑y 圈.
根据题意,得
解得
2x+2y=1
6x-6y=1
答:甲每分跑 圈,乙每分跑 圈.
7.用1块A型钢板可制成2块C型钢板、1块D型钢板;用1块B型钢板可制成1块C型钢板、2块D型钢板现需15块C型钢板、18块D型钢板,可恰好用A型钢板、B型钢板各多少块?
【选自教材P111 复习题8 第7题】
解:设恰好用x 块A型钢板,y 块B型钢板.
根据题意,得
解得
2x+y=15
x+2y=18
x=4
y=7
答:恰好用4块A型钢板,7块B型钢板.
8. (我国古代问题)有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,音hu,是古代的一种容量单位),1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛?
【选自教材P112 复习题8 第8题】
解:设1个大桶可盛酒x斛, 1个小桶可盛酒y斛.
根据题意,得
解得
5x+y=3
x+5y=2
答:1个大桶可盛酒 斛,1个小桶可盛酒 斛.
9.现有1角、5角、1元硬币各10枚,从中取出15枚,共值7元.1角、5角、1元硬币各取多少枚?
解:设取x枚1角硬币,y枚5角硬币.
根据题意,得0.1x+0.5y+(15-x-y)=7 .
化简,得方程9x+5y=80.根据0≤x≤10, 0≤y≤10,
得x=5,y=7,15-x-y=3.
【选自教材P112 复习题8 第9题】
10.某电脑公司有A型、B型、C型三种型号的电脑,其中A型每台6000元、B型每台4000元、C型每台2 500元.某中学现有资金100500元, 计划全部用于从这家电脑公司购进36台两种型号的电脑.请你设计几种不同的购买方案供这个学校选择,并说明理由。
【选自教材P112 复习题8 第10题】
解:设从这家电脑公司购进A型电脑x台、B型电脑y台、C型电脑z台.分以下三种情况考虑.
(1)只购进A型电脑和B型电脑,
根据题意,得
解得 不合题意,舍去.
6000x+4000y=100500
x+y=36
x=-21.75
y=57.75
(2)只购进A型电脑和C型电脑,
根据题意,得 解得
(3)只购进B型电脑和C型电脑,
根据题意,得 解得
6000x+2500z=100500
x+z=36
x=3
y=33
4000y+2500z=100500
y+z=36
y=7
z=39
综上可知,有两种方案供这个学校选择:第一种方案是购进A型电脑3台、C型电脑33台;第二种方案是购进B型电脑7台、C型电脑29台.
11. 甲地到乙地全程是3.3 km,一段上坡、一段平路、一段下坡,如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需51min,从乙地到甲地需53.4min.从甲地到乙地时,上坡、平路、下坡的路程各是多少?
【选自教材P112 复习题8 第11题】
解:设从甲地到乙地时,上坡、平路、下坡的距离分别为xkm,ykm,zkm
根据题意,得 解得
答:从甲地到乙地时,上坡、平路、下坡的距离分别为1.2km,0.6km,1.5km.
y=0.6
z=1.5
x=1.2
二元一次方程组
单元小结
8
人教版·七年级下册
实际问题
数学问题
(二元或三元一次方程组)
实际问题的答案
数学问题的解
(二元或三元一次方程组的解)
设未知数、列方程组
转化
检验
解方程组
代入法
加减法
(消元)
知识结构
考点一 二元一次方程与二元一次方程组的定义
例1 若 x2m-1 + 5y3n-2m = 7 是关于 x、y 的二元一次方程,则 m = ,n = .
1
1
关于 x、y 的二元一次方程
2m - 1 = 1,
3n - 2m = 1.
m = 1,
n = 1.
理解定义
列方程组
解方程组求出参数值
含有两个未知数,并且含有未知数的项的次数都是1, 像这样的方程叫做二元一次方程.
已知方程 (m - 3) + (n + 2) = 0 是关于 x、y 的二元一次方程,求 m、n 的值.
未知数项的次数是 1
| n | - 1 = 1
m2 - 8 = 1
m = -3
n = 2
两个未知数系数不为 0
m≠3,n≠-2
对应练习
考点二 二元一次方程与二元一次方程组的解
例2 已知 x = 1,y = -2 是关于 x、y 二元一次方程组
的解,求 a,b 的值.
解:
把 x = 1,y = -2 代入二元一次方程组得
a + 4 = 3,
1 + 2b = 4.
解得
a = -1
b = 1.5
ax - 2y = 3,
x - by = 4.
已知 x = 1,y = -2 满足 (ax - 2y - 3)2 + |x - by + 4| = 0,求 a + b 的值.
解:由题意可得
把 x = 1,y = -2 代入方程组可得
解得 ,则 a + b = -3.5.
ax - 2y - 3 = 0,
x - by + 4 = 0.
a + 4 - 3 = 0,
1 + 2b + 4 = 0.
a = -1
b = -2.5
对应练习
考点三 代入消元法与加减消元法
例3 用代入法消元法解方程组
解:
由①可得 y = 3x - 7 . ③
将③代入②得 5x + 2(3x - 7) = 8,
解得 x = 2. 把 x = 2 代入③得
y = -1.
由此可得二元一次方程组的解是
x = 2,
y = -1.
3x - y = 3,①
5x + 2y = 8.②
例4 用加减消元法解方程组
由② - ①得 18 = y + 11,解得 y = 7.
把 y = 7 代入①得 3x - 3 = 28 - 16,
解得 x = 5.
由此可得二元一次方程组的解为
x = 5,
y = 7.
解:
3( x–1 )=4( y–4 ),①
5( y–4 )=3( x+5 ). ②
二元一次方程组
消元思想
代入消元法
加减消元法
已知 -4xm+nym-n 与 -2x7-my1+n 是同类项,求 m,n 的值.
解:由题意得
解得
m + n=7 - m ,
m - n=1 + n .
m=3,
n=1.
对应练习
考点四 二元一次方程组的实际应用
例5 把一些图书分给某班学生阅读,若每人分 3 本,则剩余 20 本;若每人分 4 本,则还缺 25 本. 这个班有多少学生?图书一共多少本?
等量关系:
3×学生人数+20=图书数量
4×学生人数-25=图书数量
设这个班有x名学生,图书一共有y本.
3x+20=y
4x-25=y
解:设该班有 x 名学生,图书一共有 y 本,则
答:这个班有 45 名学生,图书一共有 155 本.
解得
3x+20=y
4x-25=y
x=45
y=155
列二元一次方程组解决实际问题的步骤:
找等量关系
审题
设元
列方程组
解方程组
检验作答
2个未知数
根据等量关系
代入法
加减法
某校七年级安排宿舍,若每间宿舍住6人,则有4人住不下;若每间住7人,则有1间只住3人,且空余11间宿舍.问该年级寄宿学生有多少人?宿舍有多少间?
解:设该年级寄宿学生有 x 人,宿舍有 y 间.根据题意可得 解得
答:设该年级寄宿学生有514人,宿舍有85间.
6y+4=x
7×(y-11-1)=x-3
x=514
y=85
对应练习
1.用代入法解下列方程组:
(1)
a=2b+3
a=3b+20
(2)
x-y=13
x=6y-7
课堂练习
解:把①代入②,得2b+3=3b+20,解得b=-17
把b=-17代入①,得a=-31.
∴方程组的解为
a=-31
b=-17
①
②
解:把②代入①,
得6y-y-7=13,解得y=4
把y=4代入②,得x=17.
∴方程组的解为
x=17
y=4
①
②
【选自教材P111 复习题8 第1题】
(3)
x-y=4
4x+2y=-1
(4)
5x-y=110
9y-x=110
解:由①,得y=x-4 ③
把③代入②,得4x+2(x-4)=-1
解得
把 代入③,得
∴方程组的解为
①
②
解:由①,得y=5x-110 ③
把③代入②,
得9(5x-110)-x=110,解得x=25
把x=25代入③,得y=15.
∴方程组的解为
x=25
y=15
①
②
2.用加减法解下列方程组:
(1)
3m+b=11
-4m-b=11
(2)
0.6x-0.4y=1.1
0.2x-0.4y=2.3
解:①+②,得-m=22,
即m=-22.
把m=-22代入①,得b=77.
∴方程组的解为
m=-22
b=77
①
②
解:①-②,得0.4x=-1.2
解得x=-3,
把x=-3代入①,得
∴方程组的解为
①
②
x=-3
【选自教材P111 复习题8 第2题】
(3)
4f+g=15
3g-4f =-3
(4)
解:①+②,得4g=12,
解得g=3.
把g=3代入①,得f=3.
∴方程组的解为
f=3
g=3
①
②
解:①-②,得2y=-8,
解得y=-4.
把y=-4代入②,得x=12.
∴方程组的解为
x=12
y=-4
①
②
3.解下列方程组:
(1)
4(x-y-1)=3(1-y)-2
解:整理方程组,得
①×2+②,得11x=22,即x=2
把x=2代入①,得4×2-y=5
解得y=3
∴原方程组的解是
x=2
y=3
①
②
4x-y=5
3x+2y=12
【选自教材P111 复习题8 第3题】
3.解下列方程组:
(2)
6(x+y)-4(2x-y)=16
解:整理方程组,得
①×2+②×5,得-22y+50y=-24+80,解得y=2
把y=2代入①,得5x-11×2=-12
解得x=3
∴原方程组的解是
x=2
y=2
①
②
5x-11y=-12
-2x+10y=16
【选自教材P111 复习题8 第3题】
4.解系列方程组:
(1)
3x-y+z=3
2x+y-3z=11
x+y+z=12
③
原方程的解为
解:①+②,得5x-2z=14.④
②-③,得x-4z=-1.⑤
④与⑤组成方程组
①
②
5x-2z=14
x-4z=-1
把 , 代入③得
解得
解这个方程组得
【选自教材P111 复习题8 第4题】
(2)
5x-4y+4z=13
2x+7y-3z=19
3x+2y-z=18
4.解系列方程组:
解:①+②+③,得10x+5y=50.④
①+③×4 ,得17x+4y=85.⑤
④与⑤组成方程组
10x+5y=50
17x+4y=85
把x=5,y=0 代入③得
3×5-z=18,解得z=-3
解这个方程组得
原方程的解为
x=5
y=0
z=-3
③
①
②
x=5
y=0
【选自教材P111 复习题8 第4题】
5. 1号仓库与2号仓库共存粮450t.现从1号仓库运出存粮的60%,从2号仓库运出存粮的40%,结果2号仓库所余粮食比1号仓库所余粮食多30t.1号仓库与2号仓库原来各存粮多少吨?
【选自教材P111 复习题8 第5题】
解:设1号仓库原来存粮x t,2号仓库原来存粮y t.
根据题意,得
解得
x+y=450
(1-0.6)x=(1-0.4)y-30
x=240
y=210
答:1号仓库原来存粮240t,2号仓库原来存粮210t.
6.甲、乙二人都以不变的速度在环形路上跑步,如果同时同地出发,反向而行,每隔2min相遇一次;如果同时同地出发,同向而行,每隔6min相遇一次,已知甲比乙跑得快,甲、乙二人每分各跑多少圈?
【选自教材P111 复习题8 第6题】
解:设甲每分跑x 圈,乙每分跑y 圈.
根据题意,得
解得
2x+2y=1
6x-6y=1
答:甲每分跑 圈,乙每分跑 圈.
7.用1块A型钢板可制成2块C型钢板、1块D型钢板;用1块B型钢板可制成1块C型钢板、2块D型钢板现需15块C型钢板、18块D型钢板,可恰好用A型钢板、B型钢板各多少块?
【选自教材P111 复习题8 第7题】
解:设恰好用x 块A型钢板,y 块B型钢板.
根据题意,得
解得
2x+y=15
x+2y=18
x=4
y=7
答:恰好用4块A型钢板,7块B型钢板.
8. (我国古代问题)有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,音hu,是古代的一种容量单位),1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛?
【选自教材P112 复习题8 第8题】
解:设1个大桶可盛酒x斛, 1个小桶可盛酒y斛.
根据题意,得
解得
5x+y=3
x+5y=2
答:1个大桶可盛酒 斛,1个小桶可盛酒 斛.
9.现有1角、5角、1元硬币各10枚,从中取出15枚,共值7元.1角、5角、1元硬币各取多少枚?
解:设取x枚1角硬币,y枚5角硬币.
根据题意,得0.1x+0.5y+(15-x-y)=7 .
化简,得方程9x+5y=80.根据0≤x≤10, 0≤y≤10,
得x=5,y=7,15-x-y=3.
【选自教材P112 复习题8 第9题】
10.某电脑公司有A型、B型、C型三种型号的电脑,其中A型每台6000元、B型每台4000元、C型每台2 500元.某中学现有资金100500元, 计划全部用于从这家电脑公司购进36台两种型号的电脑.请你设计几种不同的购买方案供这个学校选择,并说明理由。
【选自教材P112 复习题8 第10题】
解:设从这家电脑公司购进A型电脑x台、B型电脑y台、C型电脑z台.分以下三种情况考虑.
(1)只购进A型电脑和B型电脑,
根据题意,得
解得 不合题意,舍去.
6000x+4000y=100500
x+y=36
x=-21.75
y=57.75
(2)只购进A型电脑和C型电脑,
根据题意,得 解得
(3)只购进B型电脑和C型电脑,
根据题意,得 解得
6000x+2500z=100500
x+z=36
x=3
y=33
4000y+2500z=100500
y+z=36
y=7
z=39
综上可知,有两种方案供这个学校选择:第一种方案是购进A型电脑3台、C型电脑33台;第二种方案是购进B型电脑7台、C型电脑29台.
11. 甲地到乙地全程是3.3 km,一段上坡、一段平路、一段下坡,如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需51min,从乙地到甲地需53.4min.从甲地到乙地时,上坡、平路、下坡的路程各是多少?
【选自教材P112 复习题8 第11题】
解:设从甲地到乙地时,上坡、平路、下坡的距离分别为xkm,ykm,zkm
根据题意,得 解得
答:从甲地到乙地时,上坡、平路、下坡的距离分别为1.2km,0.6km,1.5km.
y=0.6
z=1.5
x=1.2
