最新人教版七下数学 第九章 不等式与不等式组 章末复习 课件(共31张PPT)
文档属性
| 名称 | 最新人教版七下数学 第九章 不等式与不等式组 章末复习 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 17:55:11 | ||
图片预览










文档简介
(共31张PPT)
人教版·七年级下册
10
章末复习
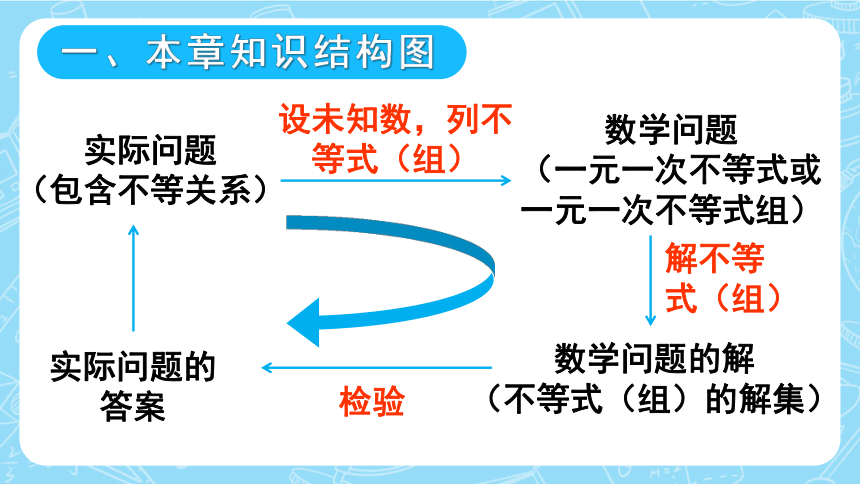
实际问题
(包含不等关系)
数学问题
(一元一次不等式或一元一次不等式组)
实际问题的
答案
数学问题的解
(不等式(组)的解集)
设未知数,列不等式(组)
检验
解不等
式(组)
一、本章知识结构图
1. 总结不等式的性质,并与等式的性质进行比较.
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果 a>b,那么 a±c>b±c.
二、回顾与思考
不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果 a>b,c>0,那么 ac>bc(或) .
不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果 a>b,c<0,那么 ac<bc(或) .
2. 总结一元一次不等式的解法,并与一元一次方程的解法进行比较.结合例子说明:解未知数为 x 的不等式,就是将不等式逐步变成 x > a 或 x < a 的形式,而不等式的性质是变形的重要依据.
①去分母
②去括号
③移项
④合并同类项
⑤系数化为1
3. 如何解一元一次不等式组?结合例子说明:解不等式组就是求有关不等式的解集的公共部分.
先求出不等式组中各不等式的解集;
再求出这些解集的公共部分.
01
02
3(x-1)+1 > 5x-2(1-x)①
5-(2x-1)< -6x ②
例 解不等式组
解:解不等式①得:x < 0
解不等式②得:x <
∴不等式组的解集为:x< .
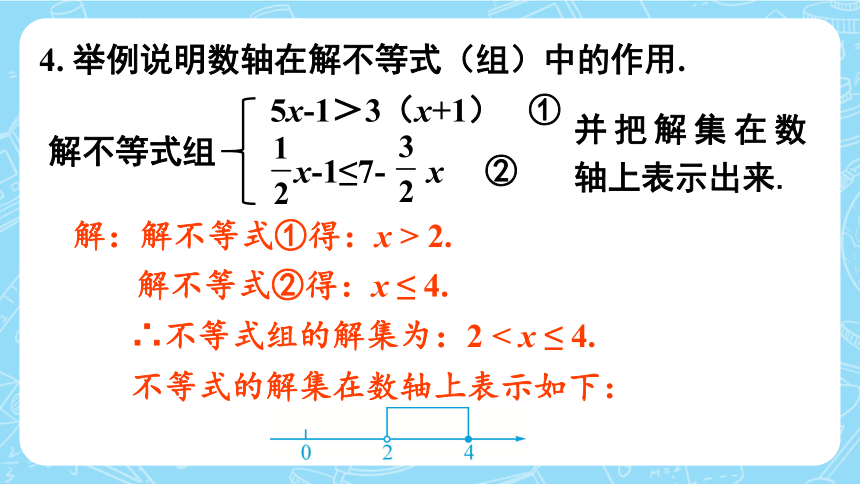
4. 举例说明数轴在解不等式(组)中的作用.
解不等式组
5x-1>3(x+1) ①
x-1≤7- x ②
并把解集在数轴上表示出来.
解:解不等式①得:x > 2.
不等式的解集在数轴上表示如下:
解不等式②得:x ≤ 4.
∴不等式组的解集为:2 < x ≤ 4.
5. 结合实例体会运用不等式解决实际问题的过程.
审:认真审题,分清已知量、未知量;
找:找出题目中的不等关系,抓住关键词,如“超过”“不大于” “最多”等;
设:设出适当的未知数;
01
02
03
答:检验答案是否符合实际意义,并作答.
列:根据题中不等关系,列出一元一次不等式;
解:求出一元一次不等式的解集;
04
05
06
5. 结合实例体会运用不等式解决实际问题的过程.
老张与老李购买了相同数量的种兔,一年后,老张养兔数比买入种兔数增加了 2 只,老李养兔数比买入种兔数的 2 倍少 1 只,老张养兔数不超过老李养兔数的 ,一年前老张至少买了多少只种兔?
解:设一年前老张买了 x 只种兔,
由题意得:2+x≤ (2x-1),
解得 x≥8.
答:一年前老张至少买了 8 只种兔.
复习巩固
1. 解下列不等式,并把它们的解集在数轴上表示出来:
(1)3(2x+7) > 23;
(2)12-4(3x-1) ≤ 2(2x-16);
(3)
(4)
复习题9
(1)3(2x+7) > 23;
解:去括号,得 6x + 21 > 23.
移项,得 6x > 23 - 21.
不等式的解为 x > .
0
(2)12-4(3x-1) ≤ 2(2x-16);
去括号,得 12-12x + 4 ≤ 4x-32.
移项,得 4x+12x ≥ 12+4+32.
合并,得 16x ≥ 48.
不等式的解为 x ≥ 3.
0
3
(3)
去分母,得 3(x + 3) < 5(2x-5)-15.
去括号,得 3x + 9 < 10x-25-15.
移项,得 10x-3x > 9+25+15.
合并,得 7x > 49.
不等式的解为 x > 7.
0
7
(4)
去分母,得 4(2x - 1) - 6(3x-1) ≥ 5.
去括号,得 8x - 4 - 18x+6 ≥ 5.
移项,得 8x - 18x ≥ 5+4-6.
合并,得 - 10x ≥ 3.
不等式的解为 x ≤ .
0
2. a 取什么值时,15-7a 的值满足下列条件?
(1)大于1; (2)小于1; (3)等于1.
解:(1) 15 – 7a > 1,7a < 14,a < 2;
(2) 15 – 7a < 1,7a > 14,a > 2;
(3) 15 – 7a = 1,7a = 14,a = 2.
3. 解下列不等式组:
(1)
2x + 1 > -1,
2x + 1 < 3;
(2)
-(x – 1) > 3,
2x + 9 > 3;
解:(1) 解①得:x > -1,解②得:x < 1,所以不等式组解集为:-1< x < 1;
①
②
①
②
(2) 解①得:x < -2,解②得:x > -3,所以不等式组解集为:-3< x < -2;
(3)
2(x-1) + x > 5x-2(1-x),
5-(2x -1) < -6x;
①
②
(3) 由①得:3x - 2 > 5x – 2 + 2x,x < 0,
由②得:5 - 2x + 1 < -6x,x < ,
所以不等式组解集为:x < ;
(4)
-3(x – 2) ≥ 4-x,
①
②
(4) 由 ① 得:-3x +6 ≥ 4–x,x ≤ 1,
由 ② 得:1 + 2x > 3x - 3,x < 4,
所以不等式组解集为:x ≤ 1;
4. 的值能否同时大于 2x + 3 和 1-x 的值?
说明理由.
解:由
解得
故所列不等式组为空集,即 不能同时大于 2x + 3 和 1- x 的值.
5. 赵军说不等式 a>2a 永远不会成立,因为如果在这个不等式两边同时除以 a,就会出现 1>2 这样的错误结论. 他的说法对吗?
解:说法错误,且解法错误. 因为由不等式性质,不等式两边同除以一个负数,那么不等号方向会改变. 又由于要使 a > 2a,则 a < 0. 因此当 a < 0 时,a > 2a 成立.
6. 解一元一次不等式组与解一元一次不等式
有什么区别和联系?
解:区别:解集不同.联系:一元一次不等式是解一元一次不等式组的基础,一元一次不等式组的解集是不等式组中各个不等式的解集的公共部分.
7. 一艘轮船从某江上游的 A 地匀速驶到下游的 B 地
用了 10 h,从 B 地匀速返回 A 地用了不到 12 h,
这段江水流速为 3 km/h,轮船在静水里的往返速
度 v 不变,v 满足什么条件?
综合运用
解:设轮船往返的静水速度为 v. AB 之间的距离为 (v+3)×10. 根据题意,得 .
解不等式,得 v > 33.
答:v 满足的条件是大于 33 千米/时.
8.老张与老李购买了相同数量的种兔,一年后,老张养兔数比买入种兔数增加了 2 只,老李养兔数比买入种兔数的 2 倍少 1 只,老张养兔数不超过老李养兔数的 ,一年前老张至少买了多少只种兔?
解:设一年前老张买了 x 只种兔,
由题意得:2+x≤ (2x-1),
解得 x≥8.
答:一年前老张至少买了 8 只种兔.
9. 三个连续正整数的和小于 333,这样的正整数有多少组?写出其中最大的一组.
解:设三个连续正整数中最大的数为 x. 根据题意,得 x -2+ x -1 + x < 333. 解不等式,得 x < 112. 从 1、2、3 开始到 109、110、111 结束,共有 109 组,其中最大的一组是 109、110、111.
拓广探索
通过这节课的学习活动,你有什么收获?
课堂总结
人教版·七年级下册
10
章末复习
实际问题
(包含不等关系)
数学问题
(一元一次不等式或一元一次不等式组)
实际问题的
答案
数学问题的解
(不等式(组)的解集)
设未知数,列不等式(组)
检验
解不等
式(组)
一、本章知识结构图
1. 总结不等式的性质,并与等式的性质进行比较.
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果 a>b,那么 a±c>b±c.
二、回顾与思考
不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果 a>b,c>0,那么 ac>bc(或) .
不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果 a>b,c<0,那么 ac<bc(或) .
2. 总结一元一次不等式的解法,并与一元一次方程的解法进行比较.结合例子说明:解未知数为 x 的不等式,就是将不等式逐步变成 x > a 或 x < a 的形式,而不等式的性质是变形的重要依据.
①去分母
②去括号
③移项
④合并同类项
⑤系数化为1
3. 如何解一元一次不等式组?结合例子说明:解不等式组就是求有关不等式的解集的公共部分.
先求出不等式组中各不等式的解集;
再求出这些解集的公共部分.
01
02
3(x-1)+1 > 5x-2(1-x)①
5-(2x-1)< -6x ②
例 解不等式组
解:解不等式①得:x < 0
解不等式②得:x <
∴不等式组的解集为:x< .
4. 举例说明数轴在解不等式(组)中的作用.
解不等式组
5x-1>3(x+1) ①
x-1≤7- x ②
并把解集在数轴上表示出来.
解:解不等式①得:x > 2.
不等式的解集在数轴上表示如下:
解不等式②得:x ≤ 4.
∴不等式组的解集为:2 < x ≤ 4.
5. 结合实例体会运用不等式解决实际问题的过程.
审:认真审题,分清已知量、未知量;
找:找出题目中的不等关系,抓住关键词,如“超过”“不大于” “最多”等;
设:设出适当的未知数;
01
02
03
答:检验答案是否符合实际意义,并作答.
列:根据题中不等关系,列出一元一次不等式;
解:求出一元一次不等式的解集;
04
05
06
5. 结合实例体会运用不等式解决实际问题的过程.
老张与老李购买了相同数量的种兔,一年后,老张养兔数比买入种兔数增加了 2 只,老李养兔数比买入种兔数的 2 倍少 1 只,老张养兔数不超过老李养兔数的 ,一年前老张至少买了多少只种兔?
解:设一年前老张买了 x 只种兔,
由题意得:2+x≤ (2x-1),
解得 x≥8.
答:一年前老张至少买了 8 只种兔.
复习巩固
1. 解下列不等式,并把它们的解集在数轴上表示出来:
(1)3(2x+7) > 23;
(2)12-4(3x-1) ≤ 2(2x-16);
(3)
(4)
复习题9
(1)3(2x+7) > 23;
解:去括号,得 6x + 21 > 23.
移项,得 6x > 23 - 21.
不等式的解为 x > .
0
(2)12-4(3x-1) ≤ 2(2x-16);
去括号,得 12-12x + 4 ≤ 4x-32.
移项,得 4x+12x ≥ 12+4+32.
合并,得 16x ≥ 48.
不等式的解为 x ≥ 3.
0
3
(3)
去分母,得 3(x + 3) < 5(2x-5)-15.
去括号,得 3x + 9 < 10x-25-15.
移项,得 10x-3x > 9+25+15.
合并,得 7x > 49.
不等式的解为 x > 7.
0
7
(4)
去分母,得 4(2x - 1) - 6(3x-1) ≥ 5.
去括号,得 8x - 4 - 18x+6 ≥ 5.
移项,得 8x - 18x ≥ 5+4-6.
合并,得 - 10x ≥ 3.
不等式的解为 x ≤ .
0
2. a 取什么值时,15-7a 的值满足下列条件?
(1)大于1; (2)小于1; (3)等于1.
解:(1) 15 – 7a > 1,7a < 14,a < 2;
(2) 15 – 7a < 1,7a > 14,a > 2;
(3) 15 – 7a = 1,7a = 14,a = 2.
3. 解下列不等式组:
(1)
2x + 1 > -1,
2x + 1 < 3;
(2)
-(x – 1) > 3,
2x + 9 > 3;
解:(1) 解①得:x > -1,解②得:x < 1,所以不等式组解集为:-1< x < 1;
①
②
①
②
(2) 解①得:x < -2,解②得:x > -3,所以不等式组解集为:-3< x < -2;
(3)
2(x-1) + x > 5x-2(1-x),
5-(2x -1) < -6x;
①
②
(3) 由①得:3x - 2 > 5x – 2 + 2x,x < 0,
由②得:5 - 2x + 1 < -6x,x < ,
所以不等式组解集为:x < ;
(4)
-3(x – 2) ≥ 4-x,
①
②
(4) 由 ① 得:-3x +6 ≥ 4–x,x ≤ 1,
由 ② 得:1 + 2x > 3x - 3,x < 4,
所以不等式组解集为:x ≤ 1;
4. 的值能否同时大于 2x + 3 和 1-x 的值?
说明理由.
解:由
解得
故所列不等式组为空集,即 不能同时大于 2x + 3 和 1- x 的值.
5. 赵军说不等式 a>2a 永远不会成立,因为如果在这个不等式两边同时除以 a,就会出现 1>2 这样的错误结论. 他的说法对吗?
解:说法错误,且解法错误. 因为由不等式性质,不等式两边同除以一个负数,那么不等号方向会改变. 又由于要使 a > 2a,则 a < 0. 因此当 a < 0 时,a > 2a 成立.
6. 解一元一次不等式组与解一元一次不等式
有什么区别和联系?
解:区别:解集不同.联系:一元一次不等式是解一元一次不等式组的基础,一元一次不等式组的解集是不等式组中各个不等式的解集的公共部分.
7. 一艘轮船从某江上游的 A 地匀速驶到下游的 B 地
用了 10 h,从 B 地匀速返回 A 地用了不到 12 h,
这段江水流速为 3 km/h,轮船在静水里的往返速
度 v 不变,v 满足什么条件?
综合运用
解:设轮船往返的静水速度为 v. AB 之间的距离为 (v+3)×10. 根据题意,得 .
解不等式,得 v > 33.
答:v 满足的条件是大于 33 千米/时.
8.老张与老李购买了相同数量的种兔,一年后,老张养兔数比买入种兔数增加了 2 只,老李养兔数比买入种兔数的 2 倍少 1 只,老张养兔数不超过老李养兔数的 ,一年前老张至少买了多少只种兔?
解:设一年前老张买了 x 只种兔,
由题意得:2+x≤ (2x-1),
解得 x≥8.
答:一年前老张至少买了 8 只种兔.
9. 三个连续正整数的和小于 333,这样的正整数有多少组?写出其中最大的一组.
解:设三个连续正整数中最大的数为 x. 根据题意,得 x -2+ x -1 + x < 333. 解不等式,得 x < 112. 从 1、2、3 开始到 109、110、111 结束,共有 109 组,其中最大的一组是 109、110、111.
拓广探索
通过这节课的学习活动,你有什么收获?
课堂总结
