最新人教版七下数学 第六章 实数 小结与复习课件 35张PPT
文档属性
| 名称 | 最新人教版七下数学 第六章 实数 小结与复习课件 35张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-07 07:48:18 | ||
图片预览










文档简介
(共35张PPT)
第六章 实数
小结与复习
人教版七年级下册
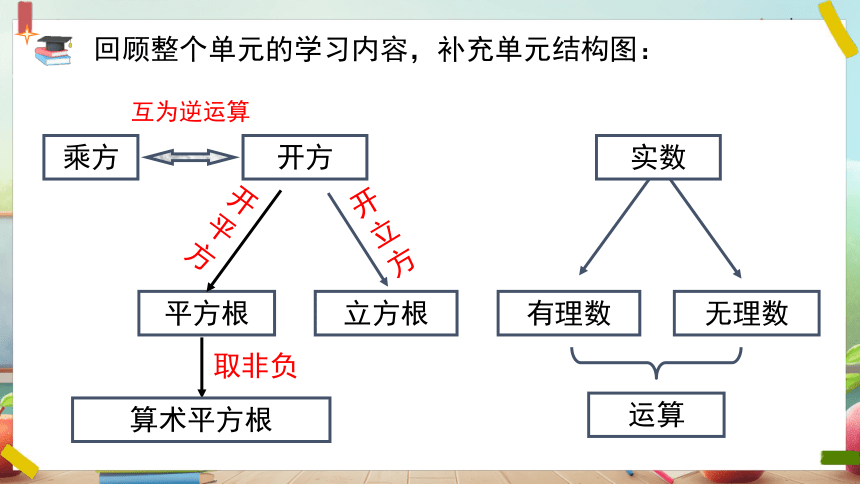
回顾整个单元的学习内容,补充单元结构图:
取非负
乘方
开方
平方根
立方根
开平方
开立方
互为逆运算
算术平方根
实数
有理数
无理数
运算
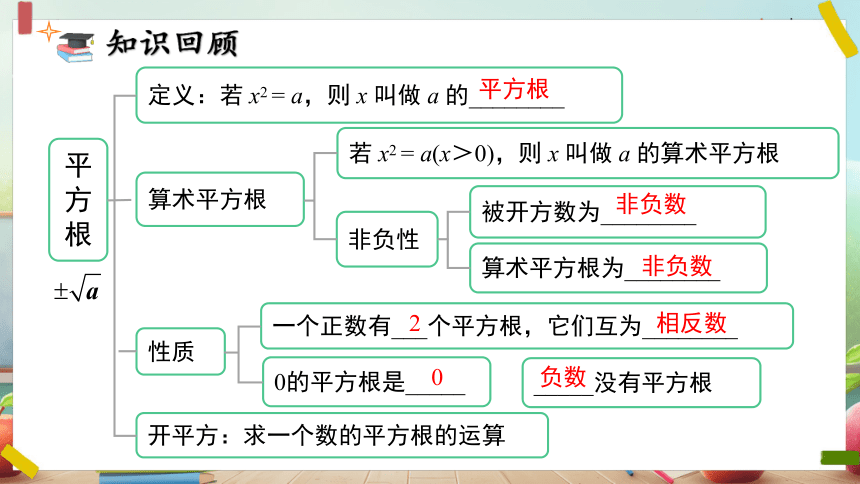
知识回顾
平方根
定义:若 x2 = a,则 x 叫做 a 的________
算术平方根
性质
若 x2 = a(x>0),则 x 叫做 a 的算术平方根
非负性
被开方数为________
算术平方根为________
一个正数有___个平方根,它们互为________
0的平方根是_____
_____没有平方根
开平方:求一个数的平方根的运算
平方根
非负数
非负数
2
0
负数
相反数
立方根
定义:若 x3 = a,则 x 叫做 a 的立方根
性质:正数的立方根是_______,负数的立方根是_______,0的立方根是_______
开立方:求一个数的立方根的运算
正数
负数
0
实数
实数的概念:无理数与有理数的统称
分类
实数的运算:与有理数的运算法则、运算律等相同
按定义:有理数和无理数
按正负:正实数:、___、负实数
实数与数轴上的点一一对应
每一个实数都可以用数轴上的一个点来表示
数轴上的一个点都表示一个实数
0
考点一 开方运算
【例1】1. 求下列各数的算术平方根及平方根:
2. 求下列各数的立方根:
解题时,要注意题目的要求,是求平方根、立方根还是求算术平方根,要注意所求结果处理.
平方根:
算术平方根:
±8
8
±0.5
0.5
±125
125
±100
100
算术平方根 平方根
【教材P61 复习题6 第1题】
【教材P61 复习题6 第2题】
【例1】1. 求下列各数的算术平方根及平方根:
2. 求下列各数的立方根:
= -0.2
= 9
立方根
【教材P61 复习题6 第1题】
【教材P61 复习题6 第2题】
考点一 开方运算
1.求下列各式的值:
= -1
= 0.4
= 0.3
【教材P61 复习题6 第3题】
<针对训练>
【例2】把下列各数写入相应的集合中:
0,0.121 221 222 1……(相邻的两个1之间依次多一个2).
非负有理数集合:{ …};
无理数集合:{ …}.
0.121 221 222 1……(相邻的两个1之间依次多一个2)
= -2
=6
对实数进行分类不能只看表面形式,应先化简,再根据结果去判断.
考点二 实数的有关概念
常见的无理数的形式:
(1)开方开不尽的数,如 , 等;
(2)π及化简后含有π的式子,如π,2-π等;
(3)有特殊特征的数,如1.212212 221…(相邻的两个1之间依次多一个2)等;
(4)有理数和无理数的和、差,如 , 等.
2.(1)有没有最小的正整数?有没有最小的整数?
(2)有没有最小的有理数?有没有最小的无理数?
(3)有没有最小的正实数?有没有最小的实数?
解:(1)有最小的正整数1,没有最小的整数;
(2)没有最小的有理数,没有最小的无理数;
(3)没有最小的正实数,没有最小的实数.
<针对训练>
【教材P57 习题6.3 第7题】
【例3】如图,若数轴上点A,B对应的实数分别为 和 ,以点B为圆心,BA长为半径画弧与数轴正半轴交点C,则点C对应的实数是( )
C
实数与数轴上的点是一一对应的关系。
考点三 实数与数轴
3. 如图,数轴上与 1, 对应的点分别是为 A、B,点 B 关于点 A 的对称点为 C,设点 C 表示的数为 x,则
.
<针对训练>
【例4】下列各数分别介于哪两个相邻的整数之间?
【教材P61 复习题6 第4题】
解:(1)5和6;
(2)6和7;
(3)4和5.
在数轴上表示的数,右边的数总是比左边的数大.
无理数的估算通常采用“夹逼法”.无理数的估算可以用来判断无理数的大小范围,也可以用来比较实数的大小.
考点三 实数的大小比较与估算
4. 比较大小: ______1.(填“>”或“<”或“=”)
<
<针对训练>
开立方运算时要注意小数点的变化规律,开立方是三位与一位的关系,开平方是二位与一位的关系.
【例5】(1) ; (2) .
=60
=y - 1
【例6】已知
则 , .
0.08138
37.77
考点四 实数的性质及运算
【例7】计算: .
【例8】计算:
实数的相反数、绝对值的性质与有理数的性质相同.
实数的运算法则与运算顺序跟有理数的是相同的.不同的是,在进行实数的运算时,可先化简含根号的数.
5. (1) 的相反数是______, 的相反数是______,
(2) 的绝对值是______,3-π 的绝对值是______,
(3)计算:
(4)如果x2=49,| y-1 |=5,那么 x + y 的值为___________.
<针对训练>
1.0,1,2,3,4,5,6,7,8,9,10的平方根及立方根中,哪些是有理数?哪些是无理数?
【教材P61 复习题6 第6题】
随堂训练
2.用计算器求下列各式的值(精确到0.001):
【教材P61 复习题6 第5题】
3.已知 m,n满足 ,则m+2n的值为____.
4.《代数学》卷首有“代数之法,无论何数,皆可以任何记号代之”,说明了所谓“代数”,就是用符号来代表数字的一种数学方法.若一个正数的平方根分别是2a-3和5-a,则这个正数是_____.
49
3
5.在比较 与13的大小关系时,我们可以把它们分别平方: 132=169,依据正数越大,其算术平方根越大,得到 >13.请利用上面的方法回答下面的问题:
比较大小: (填“>”“<”或“=”)
>
6.比较下列各组数的大小:
【教材P61 复习题6 第7题】
7.计算:
【教材P61 复习题6 第8题】
8.计算下列各式的值:
9.已知(x-1)2=4,求x的值.
解:当 x-1= 2时,x = 3
当 x-1= -2时,x = -1
所以 x 等于-1和3.
【教材P61 复习题6 第9题】
10.已知|x|<2π,x是整数,求x的值,并在数轴上表示求得的数.
【教材P61 复习题6 第10题】
∵|x|<2π
∴|x|<2π<7
∴-7<x<7
∴x =0,±1,±2,±3,±4,±5,±6
11.天气晴朗时,一个人能看到大海的最远距离s(单位:km)可用公式s2=16.88h来估计,其中h(单位:m)是眼睛离海平面的高度.如果一个人站在岸边观察,当眼睛离海平面的高度是1.5 m时,能看到多远(精确到0.01 km)?如果登上一个观望台,当眼睛离海平面的高度是35 m时,能看到多远(精确到0.01 km)?
【教材P62 复习题6 第11题】
s2=16.88h
当 h =1.5m时,s2 = 16.88×1.5 = 25.32(km) s ≈ 5.03km
当 h =35m时,s2 = 16.88×35 = 590.8(km) s ≈ 24.31km
12.一个圆与一个正方形的面积都是2 cm2,它们中哪一个的周长比较大?你能从中得到什么启示?
【教材P62 复习题6 第12题】
当 S圆 =2时,2 = πr2 , , C = 2πr =
当 S正方形 =2时,2 = a2 , ,C = 4a =
正方形的周长较大
在面积相等的圆和正方形中,圆的周长小于正方形的周长.
13.要生产一种容积为500 L的球形容器,这种球形容器的半径是多少分米(结果保留小数点后两位)?(球的体积公式是 ,其中R是球的半径.)
500 L = 500 dm3
【教材P62 复习题6 第13题】
14.填空:
(1)一个数的平方等于它本身,这个数是_______;一个数的平方根等于它本身,这个数是_______;一个数的算术平方根等于它本身,这个数是_______.
(2)一个数的立方等于它本身,这个数是________;一个数的立方根等于它本身,这个数是________.
【教材P62 复习题6 第14题】
0或1
0
0或1
0或±1
0或±1
15.【阅读材料】因为 ,即 ,所以
,所以 的整数部分为1,小数部分为
【解决问题】(1) 的小数部分是________;
(2)已知a是 的整数部分,b是 的小数部分,求 的值.
请回顾、整理你曾在实数运算中出现的错误,通过错题本等形式并尝试分类归纳,总结若干关于实数运算的经验教训,并与其他同学分享.
错题本示例:
第六章 实数
小结与复习
人教版七年级下册
回顾整个单元的学习内容,补充单元结构图:
取非负
乘方
开方
平方根
立方根
开平方
开立方
互为逆运算
算术平方根
实数
有理数
无理数
运算
知识回顾
平方根
定义:若 x2 = a,则 x 叫做 a 的________
算术平方根
性质
若 x2 = a(x>0),则 x 叫做 a 的算术平方根
非负性
被开方数为________
算术平方根为________
一个正数有___个平方根,它们互为________
0的平方根是_____
_____没有平方根
开平方:求一个数的平方根的运算
平方根
非负数
非负数
2
0
负数
相反数
立方根
定义:若 x3 = a,则 x 叫做 a 的立方根
性质:正数的立方根是_______,负数的立方根是_______,0的立方根是_______
开立方:求一个数的立方根的运算
正数
负数
0
实数
实数的概念:无理数与有理数的统称
分类
实数的运算:与有理数的运算法则、运算律等相同
按定义:有理数和无理数
按正负:正实数:、___、负实数
实数与数轴上的点一一对应
每一个实数都可以用数轴上的一个点来表示
数轴上的一个点都表示一个实数
0
考点一 开方运算
【例1】1. 求下列各数的算术平方根及平方根:
2. 求下列各数的立方根:
解题时,要注意题目的要求,是求平方根、立方根还是求算术平方根,要注意所求结果处理.
平方根:
算术平方根:
±8
8
±0.5
0.5
±125
125
±100
100
算术平方根 平方根
【教材P61 复习题6 第1题】
【教材P61 复习题6 第2题】
【例1】1. 求下列各数的算术平方根及平方根:
2. 求下列各数的立方根:
= -0.2
= 9
立方根
【教材P61 复习题6 第1题】
【教材P61 复习题6 第2题】
考点一 开方运算
1.求下列各式的值:
= -1
= 0.4
= 0.3
【教材P61 复习题6 第3题】
<针对训练>
【例2】把下列各数写入相应的集合中:
0,0.121 221 222 1……(相邻的两个1之间依次多一个2).
非负有理数集合:{ …};
无理数集合:{ …}.
0.121 221 222 1……(相邻的两个1之间依次多一个2)
= -2
=6
对实数进行分类不能只看表面形式,应先化简,再根据结果去判断.
考点二 实数的有关概念
常见的无理数的形式:
(1)开方开不尽的数,如 , 等;
(2)π及化简后含有π的式子,如π,2-π等;
(3)有特殊特征的数,如1.212212 221…(相邻的两个1之间依次多一个2)等;
(4)有理数和无理数的和、差,如 , 等.
2.(1)有没有最小的正整数?有没有最小的整数?
(2)有没有最小的有理数?有没有最小的无理数?
(3)有没有最小的正实数?有没有最小的实数?
解:(1)有最小的正整数1,没有最小的整数;
(2)没有最小的有理数,没有最小的无理数;
(3)没有最小的正实数,没有最小的实数.
<针对训练>
【教材P57 习题6.3 第7题】
【例3】如图,若数轴上点A,B对应的实数分别为 和 ,以点B为圆心,BA长为半径画弧与数轴正半轴交点C,则点C对应的实数是( )
C
实数与数轴上的点是一一对应的关系。
考点三 实数与数轴
3. 如图,数轴上与 1, 对应的点分别是为 A、B,点 B 关于点 A 的对称点为 C,设点 C 表示的数为 x,则
.
<针对训练>
【例4】下列各数分别介于哪两个相邻的整数之间?
【教材P61 复习题6 第4题】
解:(1)5和6;
(2)6和7;
(3)4和5.
在数轴上表示的数,右边的数总是比左边的数大.
无理数的估算通常采用“夹逼法”.无理数的估算可以用来判断无理数的大小范围,也可以用来比较实数的大小.
考点三 实数的大小比较与估算
4. 比较大小: ______1.(填“>”或“<”或“=”)
<
<针对训练>
开立方运算时要注意小数点的变化规律,开立方是三位与一位的关系,开平方是二位与一位的关系.
【例5】(1) ; (2) .
=60
=y - 1
【例6】已知
则 , .
0.08138
37.77
考点四 实数的性质及运算
【例7】计算: .
【例8】计算:
实数的相反数、绝对值的性质与有理数的性质相同.
实数的运算法则与运算顺序跟有理数的是相同的.不同的是,在进行实数的运算时,可先化简含根号的数.
5. (1) 的相反数是______, 的相反数是______,
(2) 的绝对值是______,3-π 的绝对值是______,
(3)计算:
(4)如果x2=49,| y-1 |=5,那么 x + y 的值为___________.
<针对训练>
1.0,1,2,3,4,5,6,7,8,9,10的平方根及立方根中,哪些是有理数?哪些是无理数?
【教材P61 复习题6 第6题】
随堂训练
2.用计算器求下列各式的值(精确到0.001):
【教材P61 复习题6 第5题】
3.已知 m,n满足 ,则m+2n的值为____.
4.《代数学》卷首有“代数之法,无论何数,皆可以任何记号代之”,说明了所谓“代数”,就是用符号来代表数字的一种数学方法.若一个正数的平方根分别是2a-3和5-a,则这个正数是_____.
49
3
5.在比较 与13的大小关系时,我们可以把它们分别平方: 132=169,依据正数越大,其算术平方根越大,得到 >13.请利用上面的方法回答下面的问题:
比较大小: (填“>”“<”或“=”)
>
6.比较下列各组数的大小:
【教材P61 复习题6 第7题】
7.计算:
【教材P61 复习题6 第8题】
8.计算下列各式的值:
9.已知(x-1)2=4,求x的值.
解:当 x-1= 2时,x = 3
当 x-1= -2时,x = -1
所以 x 等于-1和3.
【教材P61 复习题6 第9题】
10.已知|x|<2π,x是整数,求x的值,并在数轴上表示求得的数.
【教材P61 复习题6 第10题】
∵|x|<2π
∴|x|<2π<7
∴-7<x<7
∴x =0,±1,±2,±3,±4,±5,±6
11.天气晴朗时,一个人能看到大海的最远距离s(单位:km)可用公式s2=16.88h来估计,其中h(单位:m)是眼睛离海平面的高度.如果一个人站在岸边观察,当眼睛离海平面的高度是1.5 m时,能看到多远(精确到0.01 km)?如果登上一个观望台,当眼睛离海平面的高度是35 m时,能看到多远(精确到0.01 km)?
【教材P62 复习题6 第11题】
s2=16.88h
当 h =1.5m时,s2 = 16.88×1.5 = 25.32(km) s ≈ 5.03km
当 h =35m时,s2 = 16.88×35 = 590.8(km) s ≈ 24.31km
12.一个圆与一个正方形的面积都是2 cm2,它们中哪一个的周长比较大?你能从中得到什么启示?
【教材P62 复习题6 第12题】
当 S圆 =2时,2 = πr2 , , C = 2πr =
当 S正方形 =2时,2 = a2 , ,C = 4a =
正方形的周长较大
在面积相等的圆和正方形中,圆的周长小于正方形的周长.
13.要生产一种容积为500 L的球形容器,这种球形容器的半径是多少分米(结果保留小数点后两位)?(球的体积公式是 ,其中R是球的半径.)
500 L = 500 dm3
【教材P62 复习题6 第13题】
14.填空:
(1)一个数的平方等于它本身,这个数是_______;一个数的平方根等于它本身,这个数是_______;一个数的算术平方根等于它本身,这个数是_______.
(2)一个数的立方等于它本身,这个数是________;一个数的立方根等于它本身,这个数是________.
【教材P62 复习题6 第14题】
0或1
0
0或1
0或±1
0或±1
15.【阅读材料】因为 ,即 ,所以
,所以 的整数部分为1,小数部分为
【解决问题】(1) 的小数部分是________;
(2)已知a是 的整数部分,b是 的小数部分,求 的值.
请回顾、整理你曾在实数运算中出现的错误,通过错题本等形式并尝试分类归纳,总结若干关于实数运算的经验教训,并与其他同学分享.
错题本示例:
