2024年江苏省南通市海安市中考复习前数学摸底考试模拟试卷(含答案)
文档属性
| 名称 | 2024年江苏省南通市海安市中考复习前数学摸底考试模拟试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 18:41:09 | ||
图片预览



文档简介
2024年江苏省南通市海安市中考复习前数学摸底考试模拟试卷
一、选择题(本大四共10小题,每小题3分,共30分)
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2. 手机移动支付给生活带来便捷.如图是小颖某天微信账单的收支明细(正数表示收入,负数表示支出,单位:元),小颖当天微信收支的最终结果是( )
A. 收入18元 B. 收入6元 C. 支出6元 D. 支出12元
3. 若点C是线段中点,且,则的长是( )
A. B. C. D.
4. 据国家统计局数据,2023年中国国内生产总值约1260000亿元将1260000用科学记数法表示为( )
A. 0.126×107 B. 1.26×107 C. 0.126×106 D. 1.26×106
5. 下列图形中,能围成正方体的是( )
A. B. C. D.
6. 用配方法解一元二次方程时,将它化为的形式,则的值为( )
A. B. C. D.
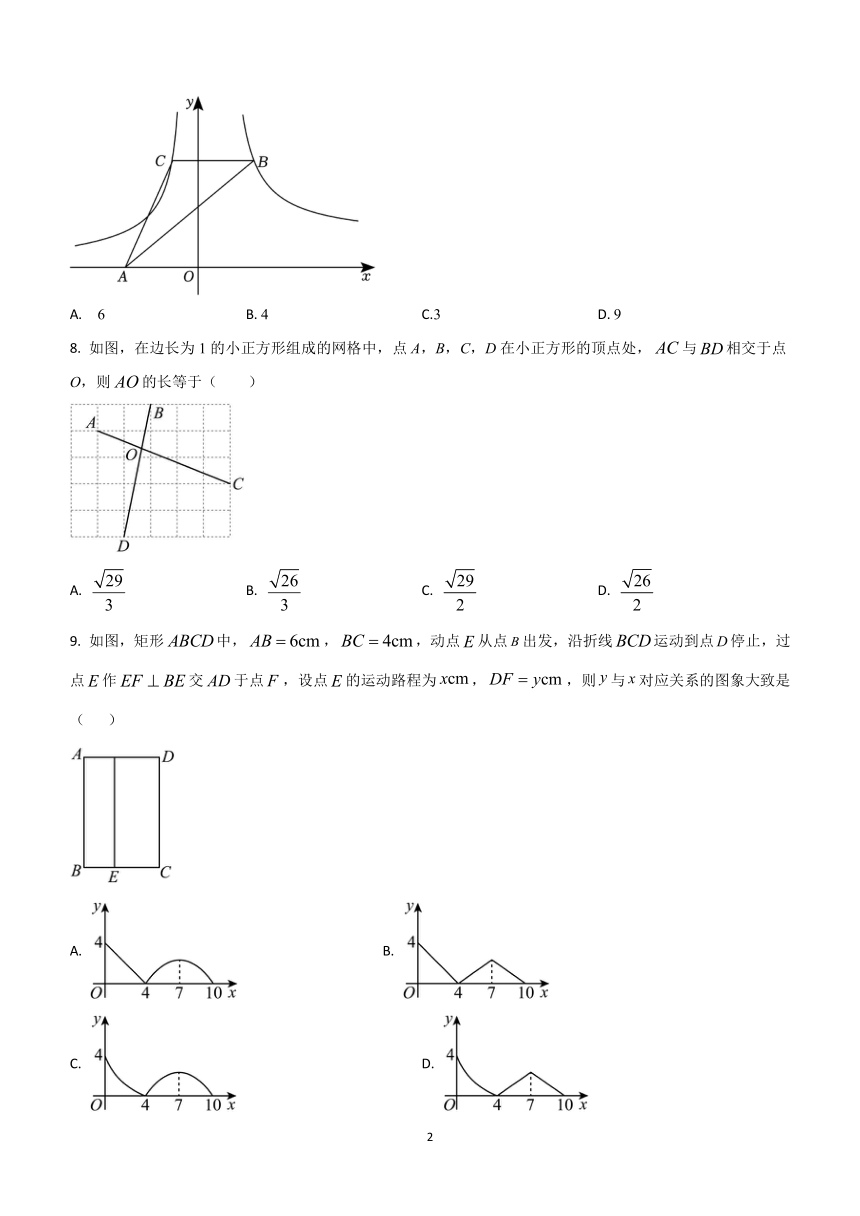
7. 如图,、两点分别在函数 和 的图象上,线段轴,点在轴上,则的面积为( )
A. 6 B. 4 C.3 D. 9
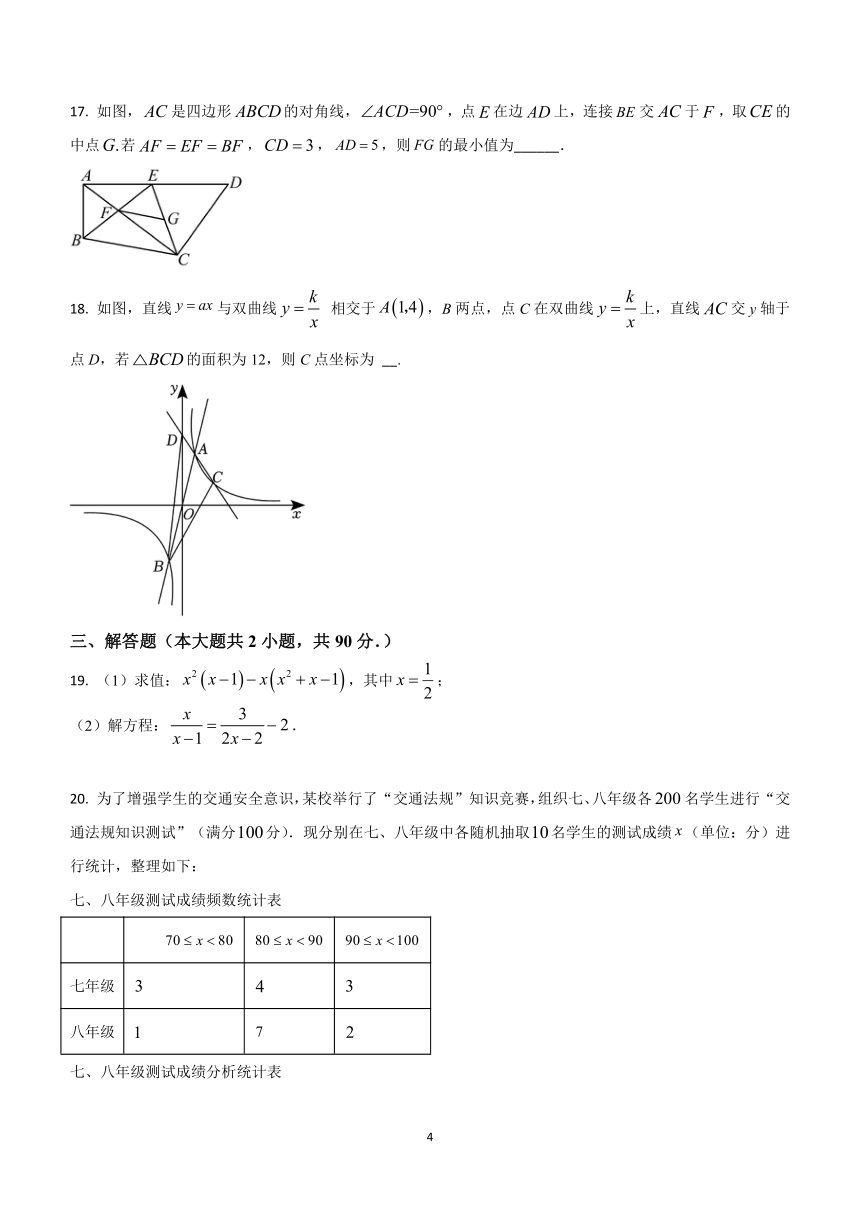
8. 如图,在边长为1的小正方形组成的网格中,点A,B,C,D在小正方形的顶点处,与相交于点O,则的长等于( )
A. B. C. D.
9. 如图,矩形中,,,动点从点出发,沿折线运动到点停止,过点作交于点,设点的运动路程为,,则与对应关系的图象大致是( )
A. B.
C. D.
10. 二次函数的图象与x轴相交于A,B两点,点C在二次函数图象上,且到x轴距离为4,,则a的值为( )
A. 4 B. 2 C. D.
二、填空题(本大题共8小题,第11~12题每小题3分,第13~18题每小题3分,共30分)
11. 若代数式在实数范围内有意义,则x的取值范围是_______.
12. 分解因式:______.
13. 如图,,点B在直线b上,且,,那么的度数为_________.
14. 中国古代数学著作《四元玉鉴》记载了“买椽多少”问题:“六贯二一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽”.大意是:现请人代买一批椽(椽,装于屋顶以支持屋顶盖材料的木杆),这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽有x株,那么可列出的方程是 .
15. 如图,是的直径,是的内接三角形.若,,则______.
16. 如图,无人机的探测器显示,从无人机看树顶的仰角为,看树底部的俯角为,无人机与树的水平距离为,则树高为______(结果保留根号).
17. 如图,是四边形的对角线,,点在边上,连接交于,取的中点若,,,则的最小值为______.
18. 如图,直线与双曲线 相交于,B两点,点C在双曲线上,直线交y轴于点D,若的面积为12,则C点坐标为 __.
三、解答题(本大题共2小题,共90分.)
19. (1)求值:,其中;
(2)解方程:.
20. 为了增强学生的交通安全意识,某校举行了“交通法规”知识竞赛,组织七、八年级各名学生进行“交通法规知识测试”(满分分).现分别在七、八年级中各随机抽取名学生的测试成绩(单位:分)进行统计,整理如下:
七、八年级测试成绩频数统计表
七年级
八年级
七、八年级测试成绩分析统计表
平均数 中位数 众数 方差
七年级
八年级
根据以上信息,解答下列问题:
(1)规定分数不低于分记为“优秀”,估计这两个年级测试成绩达到“优秀”的学生总人数一共是多少?
(2)根据以上的数据分析,任选两个角度评价七八两个年级的学生掌握交通法规知识的水平.
21. 【阅读材料】
老师的问题:已知:如图,直线,点A在上,点在上.求作:菱形,使点,分别在,上 小明的作法:(1)分别以A和为圆心,大于的长为半径画弧,两弧相交于,两点;(2)作直线,分别交,于,;(3)连接,.四边形就是所求作的菱形.
【解答问题】
请你判断小明的作法是否正确,并说明理由.
22. 有同型号的,两把锁和同型号的,,三把钥匙,其中钥匙只能打开锁,钥匙只能打开锁,钥匙不能打开这两把锁.
(1)从三把钥匙中随机取出一把钥匙,取出钥匙的概率等于___________;
(2)从两把锁中随机取出一把锁,从三把钥匙中随机取出一把钥匙,求取出的钥匙恰好能打开取出的锁的概率.
23. 如图,等腰三角形的顶角,和底边相切于点,并与两腰,分别相交于,两点,连接,.
(1)求证:四边形是菱形;
(2)若的半径为2,求图中阴影部分的面积.
24. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/,这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.
(1)写出图中点B表示的实际意义;
(2)分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;
(3)若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.
25. 如图,菱形中,,,点是线段上一点(不含端点),将沿翻折,的对应边与相交于点.
(1)当时,求的长;
(2)若是等腰三角形,求的长;
(3)若,求的取值范围.
26. 在平面直角坐标系中,二次函数的图象与x轴交于A,B两点(点A在点B的左侧),C,D两点的坐标分别为,.
(1)求A,B两点的坐标;
(2)若二次函数的图象经过点C,且与平行于x轴的直线l始终有两个交点M,N(点M在点N的左侧),P为该抛物线上异于M,N的一点,点N,P的横坐标分别为n,.当n的值发生变化时,的度数是否也发生变化?若变化,请求出度数的范围;若不变,请说明理由;
(3)若二次函数的图象与线段只有一个交点,求a的取值范围.
参考答案
一、选择题
1. 【答案】B 2. 【答案】B 3. 【答案】D 4. 【答案】D
5. 【答案】B 6. 【答案】A 7. 【答案】C 8. 【答案】A
9. 【答案】A
【解析】
【分析】分别求出点在,段运动时函数的表达式,即可求解.
【详解】解:①当点在上运动时,
,
即,
其图象为一次函数图象的一部分,排除C,D;
②当点在上运动时,如图,
则,,.
,
,,
,
又,
,
,
即,
,
其图象为开口向下的二次函数图象的一部分,排除B.
故选:A.
10. 二次函数的图象与x轴相交于A,B两点,点C在二次函数图象上,且到x轴距离为4,,则a的值为( )
A. 4 B. 2 C. D.
【答案】D
【解析】
【分析】作轴,交x轴于点D,设A、B两点横坐标为x1和x2,设点,根据勾股定理进行线段之间的转换,列出方程,再根据韦达定理,即可解答.
【详解】
解:如图,作轴,
设A、B两点横坐标为x1和x2,设点,
轴,
,
,
,
,
,
整理得,,
二次函数的图象与x轴相交于A,B两点,
是的解,
,
,
,
∵点在抛物线上,
,
.
故选:D.
二、填空题
11. 【答案】 12. 【答案】 13. 【答案】
14. 【答案】 15.【答案】 16. 【答案】
17. 【答案】
【解析】
【分析】过点作于,由勾股定理求出,由求出,由,证出,根据三角形的中位线定理得到,由垂线段最短得,当时,长度最小,最小,此时四边形是矩形,由求得结果.
【详解】解:如图,过点作于,
,,
,
,
,
,
,,,
,
,
,
,
,,
,
,
,
又是的中点,
,
当时,长度最小,最小,
此时四边形是矩形,
,
的最小值,
故答案为:.
18. 【答案】
【解析】
【分析】连接,根据,求出双曲线为,设,直线的解析式为,把、代入得:,解得,得出,求出,得出,求出,即可得出点C的坐标.
【详解】解:连接,如图所示:
∵直线与双曲线 相交于,B两点,
∴,A、B关于原点对称,
∴双曲线为,
∵点C在双曲线上,
∴设,
设直线的解析式为,
把、代入得:,
解得,
∴,
∵A、B关于原点对称,
∴,
∴,
∴,
解得,
∴.
故答案为:.
【点睛】本题主要考查了反比例函数与一次函数的交点问题,求反比例函数解析式,直线与坐标轴围成的三角形面积,解题的关键是作出辅助线,根据A、B关于原点对称,得出.
三、解答题(本大题共2小题,共90分.)
19. 【答案】(1);(2)
20. 【答案】(1)名
(2)七年级的学生掌握交通法规知识的水平较好(答案不唯一)
【解析】
【分析】(1)分别求出七、八年级优秀比例,再乘以总人数即可;
(2)两组数据的平均数相同,通过方差的大小直接比较即可.
【小问1详解】
解:七年级名学生的成绩中不低于分的所占比例为:,
八年级名学生的成绩中不低于分的所占比例为:,
∴七年级测试成绩达到“优秀“的学生人数为:(名),
∴八年级测试成绩达到“优秀“的学生人数为:(名),
∴(名).
答:估计这两个年级测试成绩达到“优秀”学生总人数一共约名;
【小问2详解】
∵七、八年级测试成绩的平均数相等,七年级测试成绩的方差小于八年级测试成绩的方差,
∴七年级的学生掌握交通法规知识的水平较好(答案不唯一).
21. 【答案】小明的作法正确,理由见解析
【解析】
【分析】先利用基本作图得垂直平分,则根据线段垂直平分线的性质得到,,,再根据平行线的性质得到,进而得到,得到,所以,然后根据菱形的判定方法可判断四边形为菱形.
【详解】解:小明的作法正确,理由如下:
由作法得垂直平分,
,,,
,
,
,
,
,
四边形菱形.
22. 【答案】(1) (2)
【解析】
【分析】(1)直接由概率公式求解即可;
(2)画树状图求概率即可求解.
【小问1详解】
解:共有三把钥匙,取出钥匙的概率等于;
故答案为:.
【小问2详解】
解:据题意,可以画出如下的树状图:
由树状图知,所有可能出现的结果共有种,这些结果出现的可能性相等.
其中取出的钥匙恰好能打开取出的锁(记为事件)的结果有种.
∴.
23. 【答案】(1)见解析 (2)
【解析】
【分析】(1)连接,根据切线的性质可得,然后利用等腰三角形的三线合一性质可得,从而可得和都是等边三角形,最后利用等边三角形的性质可得,即可解答;
(2)连接交于点,利用菱形的性质可得,,,然后在中,利用勾股定理求出的长,从而求出的长,最后根据图中阴影部分的面积扇形的面积菱形的面积,进行计算即可解答.
【小问1详解】
证明:连接,
和底边相切于点,
,
,,
,
,,
和都是等边三角形,
,,
,
四边形是菱形;
【小问2详解】
解:连接交于点,
四边形是菱形,
,,,
在中,,
,
,
图中阴影部分的面积扇形的面积菱形的面积
,
图中阴影部分的面积为.
24. 【答案】(1)当销售量为60kg时,甲、乙两种苹果的销售额相等
(2),
(3)80
【解析】
【分析】(1)结合图象可知:B点表示的意义为:当销售量为60kg时,甲、乙两种苹果的销售额相等;
(2)利用待定系数法求函数解析式即可;
(3)分别表示出甲的利润,乙的利润,再根据甲、乙两种苹果的销售量均为时,它们的利润和为1500元建立方程求解即可.
【小问1详解】
解:由图可知:
B表示的实际意义:当销售量为60kg时,甲、乙两种苹果的销售额相等.
【小问2详解】
解:由图可知:过,,
设甲种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式为:,
∴,解得:,
∴甲种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式为:;
当时,乙函数图象过,,
设乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式为:,利用待定系数法得:,解得:,
∴;
当时,乙函数图象过,,
设乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式为:,利用待定系数法得:,解得:,
∴;
综上所述:乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式为;
【小问3详解】
解:甲利润为:,
乙的利润为:
∴当时,
甲乙的利润和为:,解得(舍去);
当时,
甲乙的利润和为:,解得;
∴当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.
25. 【答案】(1) (2)或4或 (3)
【解析】
【分析】(1)根据菱形性质以及折叠的性质可得是等边三角形,,,,,则,根据勾股定理求出,根据等腰直角三角形的性质可得,即可得的长;
(2)分三种情况:①当时,②当时,③当时,根据等腰三角形的性质分别求解即可;
(3)过点作于,作于,根据三角形的面积公式可得,则,由得,由点在上可得的最大值为4,当,即点与点重合时,的值最小为,可得,即可得的取值范围.
【小问1详解】
菱形中,,
∴是等边三角形,,,
∴,
由折叠得
∴
∴
在中,
∴
∴
∵,
∴
∴是等腰直角三角形,
∴
∴
【小问2详解】
若是等腰三角形,分三种情况:
①当时
由(1)知,,
∴
②当时
∵
∴
③当时,如图1,
∵
∴
∴
∴
综上,的长为或4或;
【小问3详解】
过点作于,作于
由折叠得
∴
∴
又∵
∴
∴
∵
∴
∵点在上
∴的最大值为4,当
即点与点重合时,的值最小为
∴
∴
∴的取值范围为
26. 【答案】(1)
(2)的度数不发生变化,理由见解析
(3)或或
【解析】
【分析】(1)将二次函数转化为,令,即可求出A,B两点的坐标;
(2)将代入,求出a的值,得到,利用二次函函数的对称性求出利用坐标轴中的距离求出即可得出结论;
(3)分和两种情况讨论即可.
【小问1详解】
解:,
令,则,
解得:,
点A在点B的左侧,
;
【小问2详解】
解:将代入,得:,
解得:,
二次函数的解析式为:,
点N,P的横坐标分别为n,,
,
,
的度数不发生变化;
【小问3详解】
解:,
二次函数的图象关于对称,
当时,函数图象开口向上,
则,
解得:;
当时,函数图象开口向下,
①二次函数顶点在线段上时:,
解得:;
②二次函数顶点不在线段上时:
,
解得:,
综上,a的取值范围为:或或.
一、选择题(本大四共10小题,每小题3分,共30分)
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2. 手机移动支付给生活带来便捷.如图是小颖某天微信账单的收支明细(正数表示收入,负数表示支出,单位:元),小颖当天微信收支的最终结果是( )
A. 收入18元 B. 收入6元 C. 支出6元 D. 支出12元
3. 若点C是线段中点,且,则的长是( )
A. B. C. D.
4. 据国家统计局数据,2023年中国国内生产总值约1260000亿元将1260000用科学记数法表示为( )
A. 0.126×107 B. 1.26×107 C. 0.126×106 D. 1.26×106
5. 下列图形中,能围成正方体的是( )
A. B. C. D.
6. 用配方法解一元二次方程时,将它化为的形式,则的值为( )
A. B. C. D.
7. 如图,、两点分别在函数 和 的图象上,线段轴,点在轴上,则的面积为( )
A. 6 B. 4 C.3 D. 9
8. 如图,在边长为1的小正方形组成的网格中,点A,B,C,D在小正方形的顶点处,与相交于点O,则的长等于( )
A. B. C. D.
9. 如图,矩形中,,,动点从点出发,沿折线运动到点停止,过点作交于点,设点的运动路程为,,则与对应关系的图象大致是( )
A. B.
C. D.
10. 二次函数的图象与x轴相交于A,B两点,点C在二次函数图象上,且到x轴距离为4,,则a的值为( )
A. 4 B. 2 C. D.
二、填空题(本大题共8小题,第11~12题每小题3分,第13~18题每小题3分,共30分)
11. 若代数式在实数范围内有意义,则x的取值范围是_______.
12. 分解因式:______.
13. 如图,,点B在直线b上,且,,那么的度数为_________.
14. 中国古代数学著作《四元玉鉴》记载了“买椽多少”问题:“六贯二一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽”.大意是:现请人代买一批椽(椽,装于屋顶以支持屋顶盖材料的木杆),这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽有x株,那么可列出的方程是 .
15. 如图,是的直径,是的内接三角形.若,,则______.
16. 如图,无人机的探测器显示,从无人机看树顶的仰角为,看树底部的俯角为,无人机与树的水平距离为,则树高为______(结果保留根号).
17. 如图,是四边形的对角线,,点在边上,连接交于,取的中点若,,,则的最小值为______.
18. 如图,直线与双曲线 相交于,B两点,点C在双曲线上,直线交y轴于点D,若的面积为12,则C点坐标为 __.
三、解答题(本大题共2小题,共90分.)
19. (1)求值:,其中;
(2)解方程:.
20. 为了增强学生的交通安全意识,某校举行了“交通法规”知识竞赛,组织七、八年级各名学生进行“交通法规知识测试”(满分分).现分别在七、八年级中各随机抽取名学生的测试成绩(单位:分)进行统计,整理如下:
七、八年级测试成绩频数统计表
七年级
八年级
七、八年级测试成绩分析统计表
平均数 中位数 众数 方差
七年级
八年级
根据以上信息,解答下列问题:
(1)规定分数不低于分记为“优秀”,估计这两个年级测试成绩达到“优秀”的学生总人数一共是多少?
(2)根据以上的数据分析,任选两个角度评价七八两个年级的学生掌握交通法规知识的水平.
21. 【阅读材料】
老师的问题:已知:如图,直线,点A在上,点在上.求作:菱形,使点,分别在,上 小明的作法:(1)分别以A和为圆心,大于的长为半径画弧,两弧相交于,两点;(2)作直线,分别交,于,;(3)连接,.四边形就是所求作的菱形.
【解答问题】
请你判断小明的作法是否正确,并说明理由.
22. 有同型号的,两把锁和同型号的,,三把钥匙,其中钥匙只能打开锁,钥匙只能打开锁,钥匙不能打开这两把锁.
(1)从三把钥匙中随机取出一把钥匙,取出钥匙的概率等于___________;
(2)从两把锁中随机取出一把锁,从三把钥匙中随机取出一把钥匙,求取出的钥匙恰好能打开取出的锁的概率.
23. 如图,等腰三角形的顶角,和底边相切于点,并与两腰,分别相交于,两点,连接,.
(1)求证:四边形是菱形;
(2)若的半径为2,求图中阴影部分的面积.
24. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/,这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.
(1)写出图中点B表示的实际意义;
(2)分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;
(3)若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.
25. 如图,菱形中,,,点是线段上一点(不含端点),将沿翻折,的对应边与相交于点.
(1)当时,求的长;
(2)若是等腰三角形,求的长;
(3)若,求的取值范围.
26. 在平面直角坐标系中,二次函数的图象与x轴交于A,B两点(点A在点B的左侧),C,D两点的坐标分别为,.
(1)求A,B两点的坐标;
(2)若二次函数的图象经过点C,且与平行于x轴的直线l始终有两个交点M,N(点M在点N的左侧),P为该抛物线上异于M,N的一点,点N,P的横坐标分别为n,.当n的值发生变化时,的度数是否也发生变化?若变化,请求出度数的范围;若不变,请说明理由;
(3)若二次函数的图象与线段只有一个交点,求a的取值范围.
参考答案
一、选择题
1. 【答案】B 2. 【答案】B 3. 【答案】D 4. 【答案】D
5. 【答案】B 6. 【答案】A 7. 【答案】C 8. 【答案】A
9. 【答案】A
【解析】
【分析】分别求出点在,段运动时函数的表达式,即可求解.
【详解】解:①当点在上运动时,
,
即,
其图象为一次函数图象的一部分,排除C,D;
②当点在上运动时,如图,
则,,.
,
,,
,
又,
,
,
即,
,
其图象为开口向下的二次函数图象的一部分,排除B.
故选:A.
10. 二次函数的图象与x轴相交于A,B两点,点C在二次函数图象上,且到x轴距离为4,,则a的值为( )
A. 4 B. 2 C. D.
【答案】D
【解析】
【分析】作轴,交x轴于点D,设A、B两点横坐标为x1和x2,设点,根据勾股定理进行线段之间的转换,列出方程,再根据韦达定理,即可解答.
【详解】
解:如图,作轴,
设A、B两点横坐标为x1和x2,设点,
轴,
,
,
,
,
,
整理得,,
二次函数的图象与x轴相交于A,B两点,
是的解,
,
,
,
∵点在抛物线上,
,
.
故选:D.
二、填空题
11. 【答案】 12. 【答案】 13. 【答案】
14. 【答案】 15.【答案】 16. 【答案】
17. 【答案】
【解析】
【分析】过点作于,由勾股定理求出,由求出,由,证出,根据三角形的中位线定理得到,由垂线段最短得,当时,长度最小,最小,此时四边形是矩形,由求得结果.
【详解】解:如图,过点作于,
,,
,
,
,
,
,,,
,
,
,
,
,,
,
,
,
又是的中点,
,
当时,长度最小,最小,
此时四边形是矩形,
,
的最小值,
故答案为:.
18. 【答案】
【解析】
【分析】连接,根据,求出双曲线为,设,直线的解析式为,把、代入得:,解得,得出,求出,得出,求出,即可得出点C的坐标.
【详解】解:连接,如图所示:
∵直线与双曲线 相交于,B两点,
∴,A、B关于原点对称,
∴双曲线为,
∵点C在双曲线上,
∴设,
设直线的解析式为,
把、代入得:,
解得,
∴,
∵A、B关于原点对称,
∴,
∴,
∴,
解得,
∴.
故答案为:.
【点睛】本题主要考查了反比例函数与一次函数的交点问题,求反比例函数解析式,直线与坐标轴围成的三角形面积,解题的关键是作出辅助线,根据A、B关于原点对称,得出.
三、解答题(本大题共2小题,共90分.)
19. 【答案】(1);(2)
20. 【答案】(1)名
(2)七年级的学生掌握交通法规知识的水平较好(答案不唯一)
【解析】
【分析】(1)分别求出七、八年级优秀比例,再乘以总人数即可;
(2)两组数据的平均数相同,通过方差的大小直接比较即可.
【小问1详解】
解:七年级名学生的成绩中不低于分的所占比例为:,
八年级名学生的成绩中不低于分的所占比例为:,
∴七年级测试成绩达到“优秀“的学生人数为:(名),
∴八年级测试成绩达到“优秀“的学生人数为:(名),
∴(名).
答:估计这两个年级测试成绩达到“优秀”学生总人数一共约名;
【小问2详解】
∵七、八年级测试成绩的平均数相等,七年级测试成绩的方差小于八年级测试成绩的方差,
∴七年级的学生掌握交通法规知识的水平较好(答案不唯一).
21. 【答案】小明的作法正确,理由见解析
【解析】
【分析】先利用基本作图得垂直平分,则根据线段垂直平分线的性质得到,,,再根据平行线的性质得到,进而得到,得到,所以,然后根据菱形的判定方法可判断四边形为菱形.
【详解】解:小明的作法正确,理由如下:
由作法得垂直平分,
,,,
,
,
,
,
,
四边形菱形.
22. 【答案】(1) (2)
【解析】
【分析】(1)直接由概率公式求解即可;
(2)画树状图求概率即可求解.
【小问1详解】
解:共有三把钥匙,取出钥匙的概率等于;
故答案为:.
【小问2详解】
解:据题意,可以画出如下的树状图:
由树状图知,所有可能出现的结果共有种,这些结果出现的可能性相等.
其中取出的钥匙恰好能打开取出的锁(记为事件)的结果有种.
∴.
23. 【答案】(1)见解析 (2)
【解析】
【分析】(1)连接,根据切线的性质可得,然后利用等腰三角形的三线合一性质可得,从而可得和都是等边三角形,最后利用等边三角形的性质可得,即可解答;
(2)连接交于点,利用菱形的性质可得,,,然后在中,利用勾股定理求出的长,从而求出的长,最后根据图中阴影部分的面积扇形的面积菱形的面积,进行计算即可解答.
【小问1详解】
证明:连接,
和底边相切于点,
,
,,
,
,,
和都是等边三角形,
,,
,
四边形是菱形;
【小问2详解】
解:连接交于点,
四边形是菱形,
,,,
在中,,
,
,
图中阴影部分的面积扇形的面积菱形的面积
,
图中阴影部分的面积为.
24. 【答案】(1)当销售量为60kg时,甲、乙两种苹果的销售额相等
(2),
(3)80
【解析】
【分析】(1)结合图象可知:B点表示的意义为:当销售量为60kg时,甲、乙两种苹果的销售额相等;
(2)利用待定系数法求函数解析式即可;
(3)分别表示出甲的利润,乙的利润,再根据甲、乙两种苹果的销售量均为时,它们的利润和为1500元建立方程求解即可.
【小问1详解】
解:由图可知:
B表示的实际意义:当销售量为60kg时,甲、乙两种苹果的销售额相等.
【小问2详解】
解:由图可知:过,,
设甲种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式为:,
∴,解得:,
∴甲种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式为:;
当时,乙函数图象过,,
设乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式为:,利用待定系数法得:,解得:,
∴;
当时,乙函数图象过,,
设乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式为:,利用待定系数法得:,解得:,
∴;
综上所述:乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式为;
【小问3详解】
解:甲利润为:,
乙的利润为:
∴当时,
甲乙的利润和为:,解得(舍去);
当时,
甲乙的利润和为:,解得;
∴当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.
25. 【答案】(1) (2)或4或 (3)
【解析】
【分析】(1)根据菱形性质以及折叠的性质可得是等边三角形,,,,,则,根据勾股定理求出,根据等腰直角三角形的性质可得,即可得的长;
(2)分三种情况:①当时,②当时,③当时,根据等腰三角形的性质分别求解即可;
(3)过点作于,作于,根据三角形的面积公式可得,则,由得,由点在上可得的最大值为4,当,即点与点重合时,的值最小为,可得,即可得的取值范围.
【小问1详解】
菱形中,,
∴是等边三角形,,,
∴,
由折叠得
∴
∴
在中,
∴
∴
∵,
∴
∴是等腰直角三角形,
∴
∴
【小问2详解】
若是等腰三角形,分三种情况:
①当时
由(1)知,,
∴
②当时
∵
∴
③当时,如图1,
∵
∴
∴
∴
综上,的长为或4或;
【小问3详解】
过点作于,作于
由折叠得
∴
∴
又∵
∴
∴
∵
∴
∵点在上
∴的最大值为4,当
即点与点重合时,的值最小为
∴
∴
∴的取值范围为
26. 【答案】(1)
(2)的度数不发生变化,理由见解析
(3)或或
【解析】
【分析】(1)将二次函数转化为,令,即可求出A,B两点的坐标;
(2)将代入,求出a的值,得到,利用二次函函数的对称性求出利用坐标轴中的距离求出即可得出结论;
(3)分和两种情况讨论即可.
【小问1详解】
解:,
令,则,
解得:,
点A在点B的左侧,
;
【小问2详解】
解:将代入,得:,
解得:,
二次函数的解析式为:,
点N,P的横坐标分别为n,,
,
,
的度数不发生变化;
【小问3详解】
解:,
二次函数的图象关于对称,
当时,函数图象开口向上,
则,
解得:;
当时,函数图象开口向下,
①二次函数顶点在线段上时:,
解得:;
②二次函数顶点不在线段上时:
,
解得:,
综上,a的取值范围为:或或.
同课章节目录
