鲁科版高中物理必修第二册 1.3 动能和动能定理 课件(共56张PPT)
文档属性
| 名称 | 鲁科版高中物理必修第二册 1.3 动能和动能定理 课件(共56张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 169.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-06 19:10:04 | ||
图片预览











文档简介
(共56张PPT)
第1章
功和机械能
第3节
动能和动能定理
运动的物体可以做功,说明物体运动时具有能量例如,台风、龙卷风(图1-10)等强烈的空气流动具有巨大的能量,可以拔起大树、掀翻汽车甚至摧毁房屋运动的物体具有的能量与哪些因素有关 其变化与功有着怎样的关系 本节将深入学习动能和动能定理。
动 能
1
动能的含义
01
定义:物理学中把物体因运动而具有的能量称为动能 (kinetic energy)。
人类利用动能已有很长的历史。
例如,在船上加挂风帆,利用气流的动能推动帆船前进;制造风车和水车,利用气流和水流的动能从事各种生产活动。
现在,我们能更广泛、更有效地利用气流和水流的动能来进行发电等活动。
物体动能的大小与哪些因素有关
让我们通过一个小实验来回顾初中物理介绍过的内容。
迷你实验室
影响小车动能大小的因素
如图 1-11 所示,同一小车从斜面的不同高度处由静止开始下滑,撞击放在水平面上的木块。可以发现,小车开始下滑时的高度越高,木块被撞未后运动的距离越大。
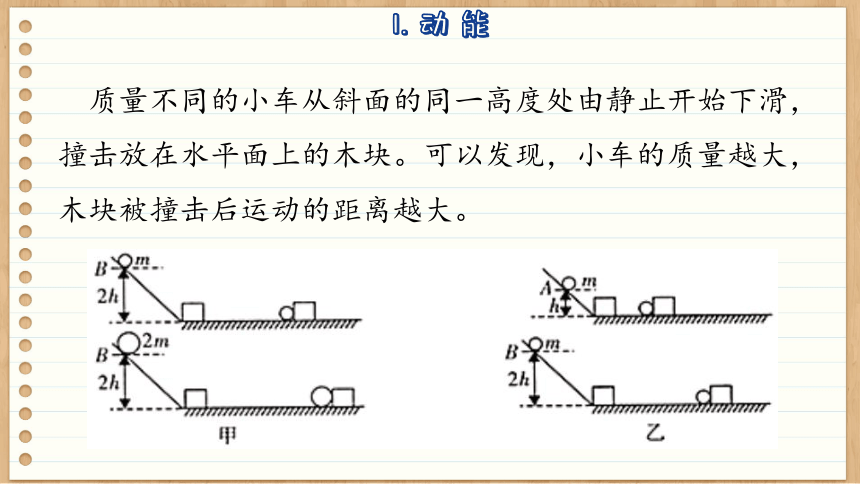
质量不同的小车从斜面的同一高度处由静止开始下滑,撞击放在水平面上的木块。可以发现,小车的质量越大,木块被撞击后运动的距离越大。
物体动能的大小与哪些因素有关
质量
速度
由以上实验可以看出,动能的大小与物体的质量和运动速度有关。物体的质量 m 越大,速度v越大,其动能就越大。在物理学中,物体的动能 Ek 表示为
Ek=mv2
特点:
标量
只有正值,没有负值
状态量
具有瞬时性
它的单位与功的单位相同,在国际单位制中都是焦耳,符号为J。从上式也可以看出
1 kg·( m/s )2=1 kg · (m/s2)· m =1 N·m =1J
外力做功与动能的变化有什么关系?
恒力做功与动能改变的关系
2
在“迷你实验室”中,小车通过撞击对木块做功,使木块从静止开始运动,木块的动能从无到有。滚动的保龄球具有动能,当其克服球瓶阻力做功时,动能减小(图1—12),那么,若外力对物体做功,该物体的动能总会
增大吗 若物体克服外力做功,该
物体的动能总会减小吗 做功与动
能的改变之间究竟有什么关系
我们从简单的情况入手,通过实验来探究恒力做功与动能改变的关系。
实验与探究
恒力做功与动能改变的关系
要研究恒力做功与动能改变的关系,需要测出作用于物体的力、物体的位移以及物体的质量和速度,求出恒力所做的功和物体的动能,然后进行比较。
用打点计时器测小车的位移和速度,用天平测小车的质量,用钩码给小车提供作用力。此实验的装置与“探究加速度与力、质量的关系”的实验装置基本相同思考实验中如何平衡摩擦力 如何让小车所受的合力近似等于钩码的重力 为什么
用打点计时器测小车的位移和速度,用天平测小车的质量,用钩码给小车提供作用力。
此实验的装置与“探究加速度与力、质量的关系”的实验装置基本相同思考实验中如何平衡摩擦力 如何让小车所受的合力近似等于钩码的重力 为什么
实验目的
探究恒力做功与动能变化的关系
实验原理
钩码拉动小车,小车的速度变化,也就是动能变化。对比小车动能的变化量 Ek、拉力对小车做的功 W=Fs (拉力近似等于钩码的重力)
G
FN
F
f
平衡摩擦
一端垫高,使小车能自由匀速直线运动
G
FN
F
f
M车>>m物
绳子拉力可近似看成钩码的重力
实验结论
误差允许的范围内,恒力做功等于动能的变化量。
G
F阻
FN
F
F2
F1
动 能
定 理
3
运用牛顿第二定律和匀变速直线运动的规律,可推导出恒力对物体做功与物体动能改变的关系。
动能变化量等于合外力做功
设一个物体的质量为 m,初速度为v1,在与其运动方向相同的合外力 F 的作用下经过一段位移s后,速度增加到v2 ,( 图1—14)。
根据牛顿第二定律和变速直线运动的规律
F=ma
s=
可得 Fs =mv22-mv12
用W表示合外力F在这一过程中所做的功,用Ek1表示物体的初动能mv12,用E表示物体的末动能mv22 ,于是有
W=Ek2- Ek1
上式表明,合外力对物体所做的功等于物体动能的变化量。这个结论称为动能定理 (theorem of kinetic energy)。
从上式可以看出,当合外力对物体做正功时,物体的末动能大于初动能,动能增大。
W=Ek2- Ek1
例如,在汽车加速的过程中,牵引力和阻力的合力对汽车做正功,汽车的动能增大。当合外力对物体做负功,或者物体克服合外力做功时,物体的末动能小于初动能,动能减小。
例如,在汽车刹车的过程中,阻力对汽车做负功,汽车的动能减小。我们可用合外力做功的多少来量度物体动能的变化量。
对动能定理的理解:
普适性
任何运动、任何力、任何过程
三同
同一对象、同一参考系、同一过程
可以证明,动能定理在物体受到变力作用或做曲线运动的情况下也是成立的。动能定理是物理学的重要规律。通过它,我们既可用做功的多少来量度动能的变化量,也可用动能的变化量来确定做功的多少,这为分析力学问题提供了新的思路。
例 题
如图1-15 所示,一辆汽车正以 v1=72 km/h 的速度匀速直线行驶,司机发现在前方150 m 处停有一故障车辆,马上进行刹车操作。
设司机的反应时间 t1=0.75 s,刹车时汽车受到的阻力为重力的。取重力加速度 g=10 m/s2。
请计算从发现故障车至停下,汽车在这段时间内发生的位移,据此判断这两辆车是否会相撞。
分析
在司机的反应时间内,后车做匀速直线运动,位移 s1=v1t1。后车刹车后,在水平方向只受到阻力 F阻 的作用,发生的位移为 s2。
根据已知条件,运用动能定理即可求出 s2,若 s1+s2<150 m,则两车不会相撞。
若研究的问题只涉及力、位移与物体运动的初、末状态,用动能定理求解通常比用牛顿运动定律求解简便得多。
对于一些变力做功问题,利用功的计算公式很难求解,通常可利用动能定理求解。
策略提炼
解:设后车刹车时所受阻力为 Fm;司机反应时间内后车的位移为 s1;从开始刹车到停止,后车的位移为 s2 。后车受力分析如图 1-16 所示。
由题意可知 v1=72 km/h=20 m/s,Fm=mg。
由匀速直线运动公式可得
s1=v1t1=20×0.75 m =15 m
由动能定理得 -F阻s2=0-mv12
整理得 s2=== m=40m,
发现故障车至停下汽车发生的位移为
s=s1+s2=55 m,
s<150m,故两车不会相撞。
讨论
从计算结果看,后车不会与前车发生追尾为避免交通事故,汽车在行驶中保持一定安全距离是很重要的。通常车速越大,需要保持的安全距离也越大。
《中华人民共和国道路交通安全法》规定机动车在道路上行驶,不得超过限速标志标明的最高时速。你能从物理学的角度说明该规定的理由吗
迁 移
运用动能定理不仅可以较简便地求解一些恒力做功问题,还可求解一些特殊情况下的变力做功问题。请你解答下面的问题。
雨滴在空中下落时会受到空气阻力,空气阻力 f 的大小与雨滴下落速率 v 的二次方成正比,即 f=kv2,其中k 为常数。若质量为 m 的雨滴,从高 h 处以初速度 v0 竖直加速下落,接近落地前开始做匀速直线运动。已知重力加速度为 g,求该雨滴从高处下落到地面的过程中,空气阻力对其所做的功。
节练习
1. 若汽车行驶速度增加为原来的 2倍,则该车从开始刹车到停下的距离约将增大为原来的4 倍。请你从动能定理的角度加以解释。
解:设汽车质量为m,原来的速度大小为v,刹车阻力大小为f,刹车距离为x,则由动能定理得
-fx=m(0-v2);
若行驶速度变为 v′ = 2v,
则由动能定理得-fx= m(0 -v′2),
联立解得 x′=4x,
即刹车距离变为原来的4倍。
2. 2017年5月5日,我国自行研制的大型喷气式客机 C919 首飞成功,标志着我国大型客机项目取得重大突破。假设飞机在水平跑道上的滑跑是初速度为0的匀加速直线运动,当位移 s=1.6×103 m 时才能达到起飞所要求的速度 v=80 m/s。已知飞机质量 m=7.0×104 kg,滑跑时受到的阻力为自身重力的 0.1,取重力加速度 g=10 m/s2,求:
(1)飞机起飞时的动能;
(2)飞机滑跑过程中受到的牵引力。
(1)飞机起飞时的动能;
解:根据动能的表达式可知,飞机起飞时的动能为
Ek= mv2
=×7.0×104×802 J
= 2.24×108 J.
(2)飞机滑跑过程中受到的牵引力
解:由动能定理得 Fs - kmgs = Ek = 0
解得飞机滑跑过程中受到的牵引力
F= Ek+
代入数据得: F=2.1×105N
3. 质量为 m 的汽车在平直公路上行驶,发动机的功率 P 和汽车受到的阻力均恒定不变。在时间 t 内,汽车的速度由 v0 增加到最大速度 vmax,则此段时间内汽车沿直线运动的距离为多少
解:由汽车在此段过程的动能定理可得
Pt-f阻·x =mvmax2 - mv02 ,
可解得此段时间内汽车沿直线运动的距离
x =
4. 拖把是由拖杆和拖把头构成的清洁工具,如图所示。若某同学保持拖杆与坚直方向的夹角 θ=37°,并用沿拖杆方向的恒力 F=30 N 推动拖把头,使其由静止开始在水平地面沿直线运动,位移 s=1m。已知拖
把头的质量 m=1.6 kg,不计拖杆质量,
拖把头与地面间的动摩擦因数 μ=0.3,取
重力加速度 g=10 m/s2,sin 37°=0.6,
cos 37°=0.8,求:
(1) 摩擦力对拖把头做的功;
解:拖把头所受的摩擦力
f = μ(mg + Fcos θ)
= 0.3×(1.6×10+30×0.8)N
= 12N,
摩擦力功 Wf =-fs=-12×1J
=-12J(做负功);
(2) 拖把获得的动能。
解:推力 F 做功
WF= F·s·sin θ = 30×1×0.6J=18J,
由动能定理可知,拖把获得的动能
Ek=WF+Wf =18J-12J=6J。
5. 如图所示,木块放在光滑水平面上,一颗子弹水平射入木块。若子弹受到的平均阻力为 F阻,射入深度为 d,在此过程中木块的位移为 s,求子弹动能的减少量和木块动能的增加量。
解:对子弹,由动能定理,损失的动能为
Ek子弹= F阻(s+d);
对木块,由牛顿第三定律可知,受到动力的平均大小为F阻,由动能定理,增加的动能为
Ek木= F阻s.
*6. 假设某地强风的风速为v,空气密度为 ρ。如果把通过横截面积 S 的风的动能转化为电能,转化效率为 η,请写出电功率的表达式。
解:每秒通过横截面积S的空气质量为 m= ρ ·vS,
所以每秒通过横截面积S的空气动能为 Ek=mv2,
由题意有 η=,其中t=1s,联立解得 P=ρηSv3。
请提问
本课结束
This lesson is over
THANKS!
第1章
功和机械能
第3节
动能和动能定理
运动的物体可以做功,说明物体运动时具有能量例如,台风、龙卷风(图1-10)等强烈的空气流动具有巨大的能量,可以拔起大树、掀翻汽车甚至摧毁房屋运动的物体具有的能量与哪些因素有关 其变化与功有着怎样的关系 本节将深入学习动能和动能定理。
动 能
1
动能的含义
01
定义:物理学中把物体因运动而具有的能量称为动能 (kinetic energy)。
人类利用动能已有很长的历史。
例如,在船上加挂风帆,利用气流的动能推动帆船前进;制造风车和水车,利用气流和水流的动能从事各种生产活动。
现在,我们能更广泛、更有效地利用气流和水流的动能来进行发电等活动。
物体动能的大小与哪些因素有关
让我们通过一个小实验来回顾初中物理介绍过的内容。
迷你实验室
影响小车动能大小的因素
如图 1-11 所示,同一小车从斜面的不同高度处由静止开始下滑,撞击放在水平面上的木块。可以发现,小车开始下滑时的高度越高,木块被撞未后运动的距离越大。
质量不同的小车从斜面的同一高度处由静止开始下滑,撞击放在水平面上的木块。可以发现,小车的质量越大,木块被撞击后运动的距离越大。
物体动能的大小与哪些因素有关
质量
速度
由以上实验可以看出,动能的大小与物体的质量和运动速度有关。物体的质量 m 越大,速度v越大,其动能就越大。在物理学中,物体的动能 Ek 表示为
Ek=mv2
特点:
标量
只有正值,没有负值
状态量
具有瞬时性
它的单位与功的单位相同,在国际单位制中都是焦耳,符号为J。从上式也可以看出
1 kg·( m/s )2=1 kg · (m/s2)· m =1 N·m =1J
外力做功与动能的变化有什么关系?
恒力做功与动能改变的关系
2
在“迷你实验室”中,小车通过撞击对木块做功,使木块从静止开始运动,木块的动能从无到有。滚动的保龄球具有动能,当其克服球瓶阻力做功时,动能减小(图1—12),那么,若外力对物体做功,该物体的动能总会
增大吗 若物体克服外力做功,该
物体的动能总会减小吗 做功与动
能的改变之间究竟有什么关系
我们从简单的情况入手,通过实验来探究恒力做功与动能改变的关系。
实验与探究
恒力做功与动能改变的关系
要研究恒力做功与动能改变的关系,需要测出作用于物体的力、物体的位移以及物体的质量和速度,求出恒力所做的功和物体的动能,然后进行比较。
用打点计时器测小车的位移和速度,用天平测小车的质量,用钩码给小车提供作用力。此实验的装置与“探究加速度与力、质量的关系”的实验装置基本相同思考实验中如何平衡摩擦力 如何让小车所受的合力近似等于钩码的重力 为什么
用打点计时器测小车的位移和速度,用天平测小车的质量,用钩码给小车提供作用力。
此实验的装置与“探究加速度与力、质量的关系”的实验装置基本相同思考实验中如何平衡摩擦力 如何让小车所受的合力近似等于钩码的重力 为什么
实验目的
探究恒力做功与动能变化的关系
实验原理
钩码拉动小车,小车的速度变化,也就是动能变化。对比小车动能的变化量 Ek、拉力对小车做的功 W=Fs (拉力近似等于钩码的重力)
G
FN
F
f
平衡摩擦
一端垫高,使小车能自由匀速直线运动
G
FN
F
f
M车>>m物
绳子拉力可近似看成钩码的重力
实验结论
误差允许的范围内,恒力做功等于动能的变化量。
G
F阻
FN
F
F2
F1
动 能
定 理
3
运用牛顿第二定律和匀变速直线运动的规律,可推导出恒力对物体做功与物体动能改变的关系。
动能变化量等于合外力做功
设一个物体的质量为 m,初速度为v1,在与其运动方向相同的合外力 F 的作用下经过一段位移s后,速度增加到v2 ,( 图1—14)。
根据牛顿第二定律和变速直线运动的规律
F=ma
s=
可得 Fs =mv22-mv12
用W表示合外力F在这一过程中所做的功,用Ek1表示物体的初动能mv12,用E表示物体的末动能mv22 ,于是有
W=Ek2- Ek1
上式表明,合外力对物体所做的功等于物体动能的变化量。这个结论称为动能定理 (theorem of kinetic energy)。
从上式可以看出,当合外力对物体做正功时,物体的末动能大于初动能,动能增大。
W=Ek2- Ek1
例如,在汽车加速的过程中,牵引力和阻力的合力对汽车做正功,汽车的动能增大。当合外力对物体做负功,或者物体克服合外力做功时,物体的末动能小于初动能,动能减小。
例如,在汽车刹车的过程中,阻力对汽车做负功,汽车的动能减小。我们可用合外力做功的多少来量度物体动能的变化量。
对动能定理的理解:
普适性
任何运动、任何力、任何过程
三同
同一对象、同一参考系、同一过程
可以证明,动能定理在物体受到变力作用或做曲线运动的情况下也是成立的。动能定理是物理学的重要规律。通过它,我们既可用做功的多少来量度动能的变化量,也可用动能的变化量来确定做功的多少,这为分析力学问题提供了新的思路。
例 题
如图1-15 所示,一辆汽车正以 v1=72 km/h 的速度匀速直线行驶,司机发现在前方150 m 处停有一故障车辆,马上进行刹车操作。
设司机的反应时间 t1=0.75 s,刹车时汽车受到的阻力为重力的。取重力加速度 g=10 m/s2。
请计算从发现故障车至停下,汽车在这段时间内发生的位移,据此判断这两辆车是否会相撞。
分析
在司机的反应时间内,后车做匀速直线运动,位移 s1=v1t1。后车刹车后,在水平方向只受到阻力 F阻 的作用,发生的位移为 s2。
根据已知条件,运用动能定理即可求出 s2,若 s1+s2<150 m,则两车不会相撞。
若研究的问题只涉及力、位移与物体运动的初、末状态,用动能定理求解通常比用牛顿运动定律求解简便得多。
对于一些变力做功问题,利用功的计算公式很难求解,通常可利用动能定理求解。
策略提炼
解:设后车刹车时所受阻力为 Fm;司机反应时间内后车的位移为 s1;从开始刹车到停止,后车的位移为 s2 。后车受力分析如图 1-16 所示。
由题意可知 v1=72 km/h=20 m/s,Fm=mg。
由匀速直线运动公式可得
s1=v1t1=20×0.75 m =15 m
由动能定理得 -F阻s2=0-mv12
整理得 s2=== m=40m,
发现故障车至停下汽车发生的位移为
s=s1+s2=55 m,
s<150m,故两车不会相撞。
讨论
从计算结果看,后车不会与前车发生追尾为避免交通事故,汽车在行驶中保持一定安全距离是很重要的。通常车速越大,需要保持的安全距离也越大。
《中华人民共和国道路交通安全法》规定机动车在道路上行驶,不得超过限速标志标明的最高时速。你能从物理学的角度说明该规定的理由吗
迁 移
运用动能定理不仅可以较简便地求解一些恒力做功问题,还可求解一些特殊情况下的变力做功问题。请你解答下面的问题。
雨滴在空中下落时会受到空气阻力,空气阻力 f 的大小与雨滴下落速率 v 的二次方成正比,即 f=kv2,其中k 为常数。若质量为 m 的雨滴,从高 h 处以初速度 v0 竖直加速下落,接近落地前开始做匀速直线运动。已知重力加速度为 g,求该雨滴从高处下落到地面的过程中,空气阻力对其所做的功。
节练习
1. 若汽车行驶速度增加为原来的 2倍,则该车从开始刹车到停下的距离约将增大为原来的4 倍。请你从动能定理的角度加以解释。
解:设汽车质量为m,原来的速度大小为v,刹车阻力大小为f,刹车距离为x,则由动能定理得
-fx=m(0-v2);
若行驶速度变为 v′ = 2v,
则由动能定理得-fx= m(0 -v′2),
联立解得 x′=4x,
即刹车距离变为原来的4倍。
2. 2017年5月5日,我国自行研制的大型喷气式客机 C919 首飞成功,标志着我国大型客机项目取得重大突破。假设飞机在水平跑道上的滑跑是初速度为0的匀加速直线运动,当位移 s=1.6×103 m 时才能达到起飞所要求的速度 v=80 m/s。已知飞机质量 m=7.0×104 kg,滑跑时受到的阻力为自身重力的 0.1,取重力加速度 g=10 m/s2,求:
(1)飞机起飞时的动能;
(2)飞机滑跑过程中受到的牵引力。
(1)飞机起飞时的动能;
解:根据动能的表达式可知,飞机起飞时的动能为
Ek= mv2
=×7.0×104×802 J
= 2.24×108 J.
(2)飞机滑跑过程中受到的牵引力
解:由动能定理得 Fs - kmgs = Ek = 0
解得飞机滑跑过程中受到的牵引力
F= Ek+
代入数据得: F=2.1×105N
3. 质量为 m 的汽车在平直公路上行驶,发动机的功率 P 和汽车受到的阻力均恒定不变。在时间 t 内,汽车的速度由 v0 增加到最大速度 vmax,则此段时间内汽车沿直线运动的距离为多少
解:由汽车在此段过程的动能定理可得
Pt-f阻·x =mvmax2 - mv02 ,
可解得此段时间内汽车沿直线运动的距离
x =
4. 拖把是由拖杆和拖把头构成的清洁工具,如图所示。若某同学保持拖杆与坚直方向的夹角 θ=37°,并用沿拖杆方向的恒力 F=30 N 推动拖把头,使其由静止开始在水平地面沿直线运动,位移 s=1m。已知拖
把头的质量 m=1.6 kg,不计拖杆质量,
拖把头与地面间的动摩擦因数 μ=0.3,取
重力加速度 g=10 m/s2,sin 37°=0.6,
cos 37°=0.8,求:
(1) 摩擦力对拖把头做的功;
解:拖把头所受的摩擦力
f = μ(mg + Fcos θ)
= 0.3×(1.6×10+30×0.8)N
= 12N,
摩擦力功 Wf =-fs=-12×1J
=-12J(做负功);
(2) 拖把获得的动能。
解:推力 F 做功
WF= F·s·sin θ = 30×1×0.6J=18J,
由动能定理可知,拖把获得的动能
Ek=WF+Wf =18J-12J=6J。
5. 如图所示,木块放在光滑水平面上,一颗子弹水平射入木块。若子弹受到的平均阻力为 F阻,射入深度为 d,在此过程中木块的位移为 s,求子弹动能的减少量和木块动能的增加量。
解:对子弹,由动能定理,损失的动能为
Ek子弹= F阻(s+d);
对木块,由牛顿第三定律可知,受到动力的平均大小为F阻,由动能定理,增加的动能为
Ek木= F阻s.
*6. 假设某地强风的风速为v,空气密度为 ρ。如果把通过横截面积 S 的风的动能转化为电能,转化效率为 η,请写出电功率的表达式。
解:每秒通过横截面积S的空气质量为 m= ρ ·vS,
所以每秒通过横截面积S的空气动能为 Ek=mv2,
由题意有 η=,其中t=1s,联立解得 P=ρηSv3。
请提问
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
