10.3 平行线的性质 学习任务单 2023-2024学年沪科版数学七年级下册(含答案)
文档属性
| 名称 | 10.3 平行线的性质 学习任务单 2023-2024学年沪科版数学七年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-06 00:00:00 | ||
图片预览


文档简介
10.3 平行线的性质
素养目标
1.回顾同位角、内错角、同旁内角之间的关系.
2.通过观察、操作、探究平行线的性质,会使用符合语言表示平行线的性质.
3.能在复杂平面图形中,根据平行关系,进行各种角之间的推算.
◎重点:平行线的性质.
预习导学
知识点一 两直线平行,同位角相等
阅读教材本课时“思考”及之前的内容,回答下列问题:
1.思考:如图,利用三角尺和直尺画平行线时,我们知道同位角相等,两直线平行.反过来,如果两条直线相互平行,那么被第三条直线所截的同位角会相等吗 猜一猜.
2.操作:如图,AB∥CD,任意画一条截线EF,将各角的大小用量角器量出来填在下表中.
∠1 ∠2 ∠3 ∠4
∠5 ∠6 ∠7 ∠8
结论:表格中的四对同位角 .
【答案】1.会.
2.相等
【归纳总结】若两条平行线被第三条直线所截,则同位角相等.简单地说, .
【答案】两直线平行,同位角相等
知识点二 两直线平行,内错角相等,同旁内角互补
阅读教材“思考”部分至练习前的内容,解答下列问题:
1.如图,AB∥CD,则∠1=∠5(同位角相等).
(1)由对顶角可知∠1=∠3,所以∠3= ,即 角相等.
(2)结论:若同位角相等,则内错角也 .
2.讨论如上图,已知AB∥CD,如何说明∠4=∠6
【答案】1.(1)∠5 内错 (2)相等
2.因为AB∥CD,所以∠2=∠6,又因为∠2=∠4,所以∠4=∠6.
【归纳总结】平行线的性质2:两条平行线被第三条直线所截,内错角相等.简单地说, .
【答案】两直线平行,内错角相等
3.如上图,已知AB∥CD,则∠1=∠5.
(1)由平角的定义可知∠1+∠4= ,所以∠4+∠5= ,即同旁内角 ;
(2)结论:若同位角相等,同旁内角 .
4.讨论:如上图,已知AB∥CD,如何说明∠3+∠6=180°
【答案】3.(1)180° 180° 互补 (2)互补
4.因为∠2=∠6,∠2+∠3=180°,所以∠3+∠6=180°.
【归纳总结】平行线的性质3:两条平行线被第三条直线所截,同旁内角互补.简单地说, .
【答案】两直线平行,同旁内角互补
5.讨论:平行线的性质和判定有什么区别
【答案】5.平行线的性质是由两条直线平行得出角相等或互补,是由直线的“位置关系”到角的“数量关系”.平行线的判定正好相反.
对点自测
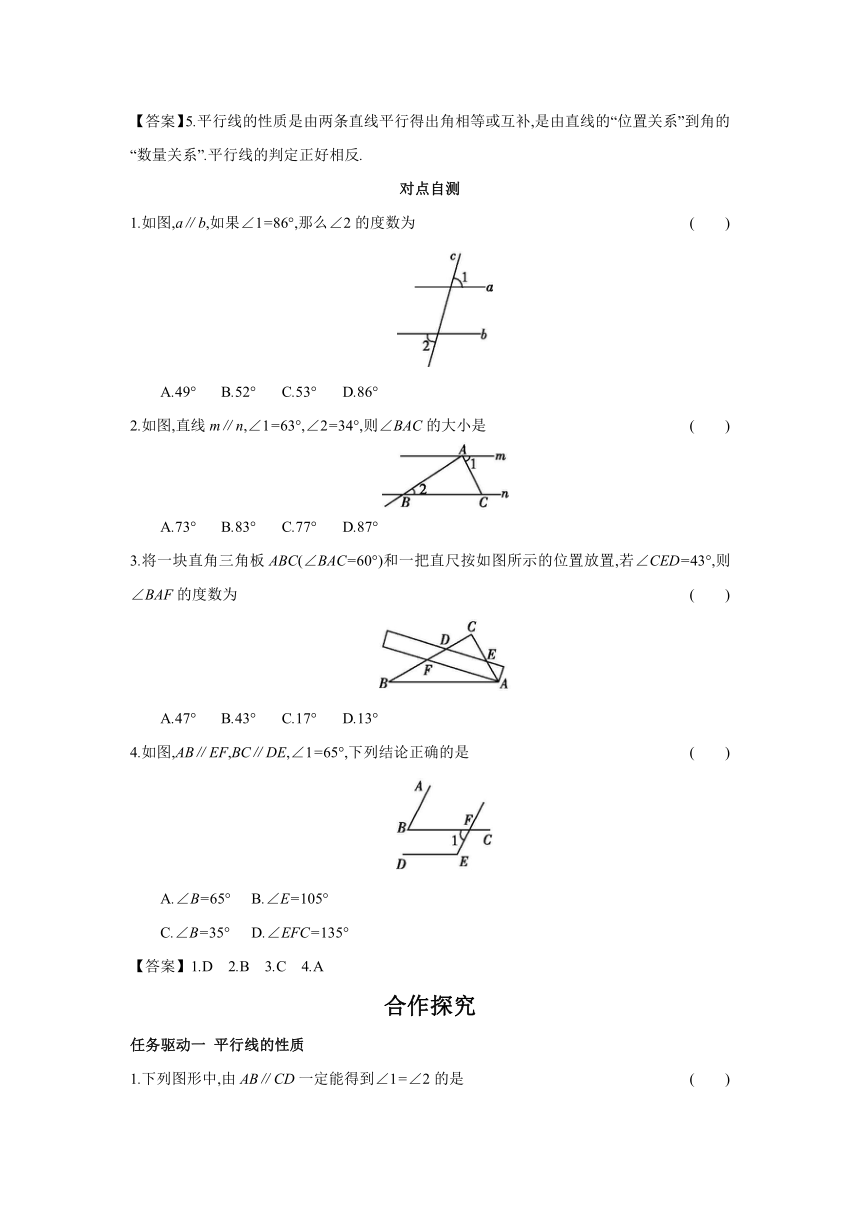
1.如图,a∥b,如果∠1=86°,那么∠2的度数为 ( )
A.49° B.52° C.53° D.86°
2.如图,直线m∥n,∠1=63°,∠2=34°,则∠BAC的大小是 ( )
A.73° B.83° C.77° D.87°
3.将一块直角三角板ABC(∠BAC=60°)和一把直尺按如图所示的位置放置,若∠CED=43°,则∠BAF的度数为 ( )
A.47° B.43° C.17° D.13°
4.如图,AB∥EF,BC∥DE,∠1=65°,下列结论正确的是 ( )
A.∠B=65° B.∠E=105°
C.∠B=35° D.∠EFC=135°
【答案】1.D 2.B 3.C 4.A
合作探究
任务驱动一 平行线的性质
1.下列图形中,由AB∥CD一定能得到∠1=∠2的是 ( )
A B
C D
2.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
3.如图,把一张长方形纸条ABCD沿AF折叠,使D落在D'处,若∠ABD=30°,AD'∥DB,则∠DAF等于多少度 (提示:长方形的四个角都是直角)
【答案】1.B
2.解:因为直线AB∥CD,∠1=65°,
所以∠ABC=∠1=65°(两直线平行,同位角相等).
因为BC平分∠ABD,所以∠ABD=2∠ABC=130°.
因为直线AB∥CD,所以∠ABD+∠BDC=180°(两直线平行,同旁内角互补),所以∠2=∠BDC=180°-∠ABD=180°-130°=50°.
3.解:因为AD'∥BD,
所以∠D'AB=∠ABD=30°(两直线平行,内错角相等),
所以∠D'AD=∠D'AB+∠BAD=30°+90°=120°,
由折叠过程可知∠DAF=∠D'AF=×120°=60°.
任务驱动二 平行线的判定与性质的综合探究
4.如图,∠B=∠CGF,∠DGF=∠F,求证:∠B+∠F=180°.
请你认真完成下面的填空.
证明:因为∠B=∠CGF( ),
所以AB∥CD( ),
所以∠B+∠BGC=180°( ).
因为∠DGF=∠F( ),∠DGF=∠BGC( ),
所以∠B+∠F=180°( ).
【答案】4.已知 同位角相等,两直线平行 两直线平行,同旁内角互补 已知 对顶角相等 等量代换
素养小测
1.如图,直线FG分别与直线AB,CD相交于点G,H,已知∠1=∠2=50°,GM平分∠HGB交直线CD于点M,则∠GMD= ( )
A.120° B.115° C.130° D.110°
2.如图,∠B=∠C,∠A=∠D,则下列结论中正确的有 (填序号).
①AB∥CD;②AE∥DF;③∠AED=∠AFD;④∠AMC=∠BND.
3.实验证明,平面镜反射光线的规律:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射,如果被b反射出的光线n与光线m平行,且∠1=37°,那么∠2的度数为 .
4.如图,折线DABCE上,已知∠A=120°,∠B=150°,当∠C= 时,AD∥CE.
5.如图,AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,猜想∠BDE与∠C有怎样的大小关系 试说明理由.
【答案】1.B 2.①②③④
3.74°
4.150°
5.解:∠BDE=∠C.
理由:因为AD⊥BC,FG⊥BC(已知),所以∠ADB=∠FGB=90°(垂直定义),所以AD∥FG(同位角相等,两直线平行),所以∠1=∠3(两直线平行,同位角相等).因为∠1=∠2(已知),所以∠2=∠3(等量代换),所以DE∥AC(内错角相等,两直线平行),所以∠BDE=∠C(两直线平行,同位角相等).
素养目标
1.回顾同位角、内错角、同旁内角之间的关系.
2.通过观察、操作、探究平行线的性质,会使用符合语言表示平行线的性质.
3.能在复杂平面图形中,根据平行关系,进行各种角之间的推算.
◎重点:平行线的性质.
预习导学
知识点一 两直线平行,同位角相等
阅读教材本课时“思考”及之前的内容,回答下列问题:
1.思考:如图,利用三角尺和直尺画平行线时,我们知道同位角相等,两直线平行.反过来,如果两条直线相互平行,那么被第三条直线所截的同位角会相等吗 猜一猜.
2.操作:如图,AB∥CD,任意画一条截线EF,将各角的大小用量角器量出来填在下表中.
∠1 ∠2 ∠3 ∠4
∠5 ∠6 ∠7 ∠8
结论:表格中的四对同位角 .
【答案】1.会.
2.相等
【归纳总结】若两条平行线被第三条直线所截,则同位角相等.简单地说, .
【答案】两直线平行,同位角相等
知识点二 两直线平行,内错角相等,同旁内角互补
阅读教材“思考”部分至练习前的内容,解答下列问题:
1.如图,AB∥CD,则∠1=∠5(同位角相等).
(1)由对顶角可知∠1=∠3,所以∠3= ,即 角相等.
(2)结论:若同位角相等,则内错角也 .
2.讨论如上图,已知AB∥CD,如何说明∠4=∠6
【答案】1.(1)∠5 内错 (2)相等
2.因为AB∥CD,所以∠2=∠6,又因为∠2=∠4,所以∠4=∠6.
【归纳总结】平行线的性质2:两条平行线被第三条直线所截,内错角相等.简单地说, .
【答案】两直线平行,内错角相等
3.如上图,已知AB∥CD,则∠1=∠5.
(1)由平角的定义可知∠1+∠4= ,所以∠4+∠5= ,即同旁内角 ;
(2)结论:若同位角相等,同旁内角 .
4.讨论:如上图,已知AB∥CD,如何说明∠3+∠6=180°
【答案】3.(1)180° 180° 互补 (2)互补
4.因为∠2=∠6,∠2+∠3=180°,所以∠3+∠6=180°.
【归纳总结】平行线的性质3:两条平行线被第三条直线所截,同旁内角互补.简单地说, .
【答案】两直线平行,同旁内角互补
5.讨论:平行线的性质和判定有什么区别
【答案】5.平行线的性质是由两条直线平行得出角相等或互补,是由直线的“位置关系”到角的“数量关系”.平行线的判定正好相反.
对点自测
1.如图,a∥b,如果∠1=86°,那么∠2的度数为 ( )
A.49° B.52° C.53° D.86°
2.如图,直线m∥n,∠1=63°,∠2=34°,则∠BAC的大小是 ( )
A.73° B.83° C.77° D.87°
3.将一块直角三角板ABC(∠BAC=60°)和一把直尺按如图所示的位置放置,若∠CED=43°,则∠BAF的度数为 ( )
A.47° B.43° C.17° D.13°
4.如图,AB∥EF,BC∥DE,∠1=65°,下列结论正确的是 ( )
A.∠B=65° B.∠E=105°
C.∠B=35° D.∠EFC=135°
【答案】1.D 2.B 3.C 4.A
合作探究
任务驱动一 平行线的性质
1.下列图形中,由AB∥CD一定能得到∠1=∠2的是 ( )
A B
C D
2.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
3.如图,把一张长方形纸条ABCD沿AF折叠,使D落在D'处,若∠ABD=30°,AD'∥DB,则∠DAF等于多少度 (提示:长方形的四个角都是直角)
【答案】1.B
2.解:因为直线AB∥CD,∠1=65°,
所以∠ABC=∠1=65°(两直线平行,同位角相等).
因为BC平分∠ABD,所以∠ABD=2∠ABC=130°.
因为直线AB∥CD,所以∠ABD+∠BDC=180°(两直线平行,同旁内角互补),所以∠2=∠BDC=180°-∠ABD=180°-130°=50°.
3.解:因为AD'∥BD,
所以∠D'AB=∠ABD=30°(两直线平行,内错角相等),
所以∠D'AD=∠D'AB+∠BAD=30°+90°=120°,
由折叠过程可知∠DAF=∠D'AF=×120°=60°.
任务驱动二 平行线的判定与性质的综合探究
4.如图,∠B=∠CGF,∠DGF=∠F,求证:∠B+∠F=180°.
请你认真完成下面的填空.
证明:因为∠B=∠CGF( ),
所以AB∥CD( ),
所以∠B+∠BGC=180°( ).
因为∠DGF=∠F( ),∠DGF=∠BGC( ),
所以∠B+∠F=180°( ).
【答案】4.已知 同位角相等,两直线平行 两直线平行,同旁内角互补 已知 对顶角相等 等量代换
素养小测
1.如图,直线FG分别与直线AB,CD相交于点G,H,已知∠1=∠2=50°,GM平分∠HGB交直线CD于点M,则∠GMD= ( )
A.120° B.115° C.130° D.110°
2.如图,∠B=∠C,∠A=∠D,则下列结论中正确的有 (填序号).
①AB∥CD;②AE∥DF;③∠AED=∠AFD;④∠AMC=∠BND.
3.实验证明,平面镜反射光线的规律:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射,如果被b反射出的光线n与光线m平行,且∠1=37°,那么∠2的度数为 .
4.如图,折线DABCE上,已知∠A=120°,∠B=150°,当∠C= 时,AD∥CE.
5.如图,AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,猜想∠BDE与∠C有怎样的大小关系 试说明理由.
【答案】1.B 2.①②③④
3.74°
4.150°
5.解:∠BDE=∠C.
理由:因为AD⊥BC,FG⊥BC(已知),所以∠ADB=∠FGB=90°(垂直定义),所以AD∥FG(同位角相等,两直线平行),所以∠1=∠3(两直线平行,同位角相等).因为∠1=∠2(已知),所以∠2=∠3(等量代换),所以DE∥AC(内错角相等,两直线平行),所以∠BDE=∠C(两直线平行,同位角相等).
